Materi matematika diskrit – Matematika Diskrit adalah cabang matematika yang berfokus pada objek-objek terhitung dan terpisah, seperti bilangan bulat, himpunan, dan graf. Tidak seperti matematika kontinu yang mempelajari objek-objek yang dapat dibagi secara tak terbatas, matematika diskrit membahas konsep-konsep yang memiliki nilai pasti dan terdefinisi dengan jelas.
Matematika Diskrit memiliki peran penting dalam berbagai bidang, mulai dari ilmu komputer dan teknologi informasi hingga ekonomi dan biologi. Dalam dunia komputer, konsep-konsep seperti algoritma, pemrograman, dan keamanan data dibangun di atas fondasi matematika diskrit. Sementara itu, di bidang lain, matematika diskrit digunakan untuk memodelkan dan menganalisis fenomena yang melibatkan objek-objek terdefinisi, seperti jaringan sosial, sistem ekonomi, dan interaksi genetik.
Pengertian Materi Matematika Diskrit
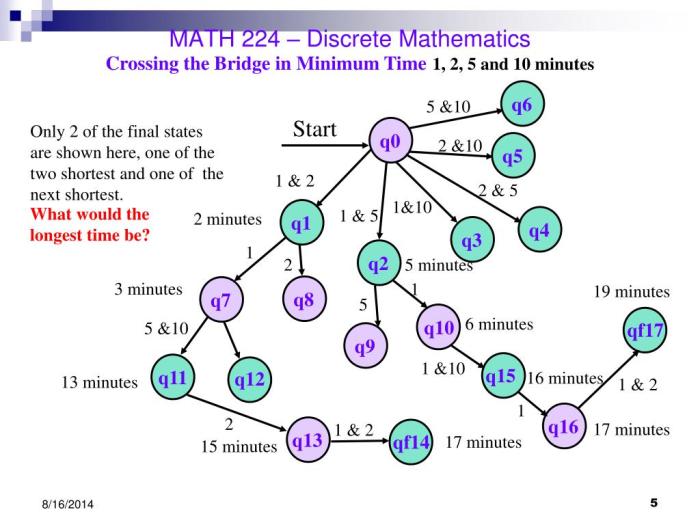
Matematika diskrit merupakan cabang ilmu matematika yang mempelajari objek-objek yang bersifat diskrit atau terputus-putus. Objek-objek ini dapat berupa bilangan bulat, himpunan, graf, dan struktur lain yang memiliki sifat terdefinisi dengan baik. Berbeda dengan matematika kontinu yang mempelajari objek-objek yang bersifat kontinu seperti garis, kurva, dan fungsi, matematika diskrit fokus pada analisis dan manipulasi objek-objek yang terdefinisi secara terpisah.
Contoh Penerapan Matematika Diskrit dalam Kehidupan Nyata
Matematika diskrit memiliki banyak aplikasi dalam berbagai bidang, seperti:
- Komputer dan Informatika: Matematika diskrit menjadi dasar dalam pengembangan algoritma, struktur data, pemrograman komputer, dan jaringan komputer. Misalnya, algoritma pencarian dan pengurutan, manajemen basis data, dan keamanan jaringan.
- Ilmu Komputer: Matematika diskrit digunakan dalam analisis dan desain sistem komputer, pengembangan perangkat lunak, dan pemodelan sistem kompleks.
- Telekomunikasi: Matematika diskrit diterapkan dalam pengkodean data, keamanan jaringan, dan optimasi aliran data dalam sistem komunikasi.
- Biologi: Matematika diskrit digunakan dalam pemodelan populasi, analisis jaringan genetik, dan studi evolusi.
- Ekonomi dan Keuangan: Matematika diskrit membantu dalam optimasi portofolio, analisis risiko, dan teori permainan.
Perbedaan Matematika Diskrit dan Matematika Kontinu
| Aspek | Matematika Diskrit | Matematika Kontinu |
|---|---|---|
| Objek Studi | Bilangan bulat, himpunan, graf, struktur diskrit | Bilangan real, fungsi kontinu, garis, kurva |
| Metode | Algoritma, logika, teori himpunan, kombinatorika | Kalkulus, analisis, geometri diferensial |
| Contoh Aplikasi | Algoritma komputer, jaringan komputer, teori permainan | Fisika, kimia, teknik, ekonomi |
Ilustrasi Perbedaan Konsep Kontinu dan Diskrit
Bayangkan sebuah garis lurus. Garis ini merupakan representasi dari konsep kontinu dalam matematika, karena setiap titik pada garis dapat dihubungkan dengan titik lain di sekitarnya. Berbeda dengan garis, bayangkan sebuah kumpulan titik yang terpisah satu sama lain. Kumpulan titik ini mewakili konsep diskrit dalam matematika, karena setiap titik memiliki identitas sendiri dan tidak terhubung langsung dengan titik di sekitarnya.
Cabang-Cabang Matematika Diskrit
Matematika diskrit adalah cabang matematika yang mempelajari objek-objek diskrit, yaitu objek-objek yang terpisahkan dan dapat dihitung. Matematika diskrit memiliki peran penting dalam berbagai bidang, termasuk ilmu komputer, teknik, ekonomi, dan ilmu sosial. Cabang-cabang matematika diskrit yang utama mencakup beberapa topik menarik yang akan kita bahas lebih lanjut.
Kombinatorika
Kombinatorika mempelajari cara menghitung dan menyusun objek-objek diskrit. Contoh topik yang dipelajari dalam kombinatorika meliputi:
- Permutasi dan kombinasi: Menghitung banyaknya cara untuk menyusun objek-objek dalam urutan tertentu atau tanpa memperhatikan urutan.
- Teori graf: Mempelajari hubungan antara objek-objek diskrit dengan menggunakan graf.
- Desain eksperimen: Mempelajari cara merancang eksperimen yang efisien untuk mendapatkan hasil yang akurat.
Teori Bilangan
Teori bilangan mempelajari sifat-sifat bilangan bulat. Contoh topik yang dipelajari dalam teori bilangan meliputi:
- Faktorisasi: Memecah bilangan bulat menjadi faktor-faktor prima.
- Kriptografi: Mempelajari teknik enkripsi dan dekripsi data.
- Teori kode: Mempelajari teknik untuk mendeteksi dan mengoreksi kesalahan dalam data.
Aljabar Abstrak
Aljabar abstrak mempelajari struktur aljabar, seperti grup, ring, dan medan. Contoh topik yang dipelajari dalam aljabar abstrak meliputi:
- Grup: Himpunan dengan operasi biner yang memenuhi sifat-sifat tertentu.
- Ring: Himpunan dengan operasi penjumlahan dan perkalian yang memenuhi sifat-sifat tertentu.
- Medan: Himpunan dengan operasi penjumlahan, perkalian, dan pembagian yang memenuhi sifat-sifat tertentu.
Logika Matematika
Logika matematika mempelajari penalaran dan pembuktian matematis. Contoh topik yang dipelajari dalam logika matematika meliputi:
- Sistem logika: Mempelajari sistem formal untuk mendeduksi kesimpulan dari premis-premis.
- Teori himpunan: Mempelajari sifat-sifat himpunan dan operasi pada himpunan.
- Teori rekursi: Mempelajari fungsi dan relasi yang dapat didefinisikan secara rekursif.
Teori Probabilitas dan Statistika
Teori probabilitas dan statistika mempelajari kemungkinan kejadian dan analisis data. Contoh topik yang dipelajari dalam teori probabilitas dan statistika meliputi:
- Probabilitas: Mempelajari kemungkinan kejadian acak.
- Statistika: Mempelajari cara mengumpulkan, menganalisis, dan menginterpretasikan data.
- Teori antrian: Mempelajari model untuk menganalisis sistem antrian.
Tabel Cabang-Cabang Matematika Diskrit, Materi matematika diskrit
| Cabang | Contoh Topik | Penerapan |
|---|---|---|
| Kombinatorika | Permutasi, kombinasi, teori graf | Ilmu komputer, teknik, statistika |
| Teori Bilangan | Faktorisasi, kriptografi, teori kode | Kriptografi, ilmu komputer, teknik |
| Aljabar Abstrak | Grup, ring, medan | Ilmu komputer, fisika, kimia |
| Logika Matematika | Sistem logika, teori himpunan, teori rekursi | Ilmu komputer, filsafat, linguistik |
| Teori Probabilitas dan Statistika | Probabilitas, statistika, teori antrian | Ilmu komputer, ekonomi, ilmu sosial |
Hubungan Antar Cabang
Cabang-cabang matematika diskrit saling melengkapi dan saling berhubungan. Contohnya, teori graf dapat digunakan untuk menyelesaikan masalah dalam kombinatorika, dan teori bilangan dapat digunakan untuk membangun sistem kriptografi yang kuat. Logika matematika menyediakan dasar untuk penalaran matematis dalam semua cabang matematika diskrit.
Konsep Dasar dalam Matematika Diskrit: Materi Matematika Diskrit
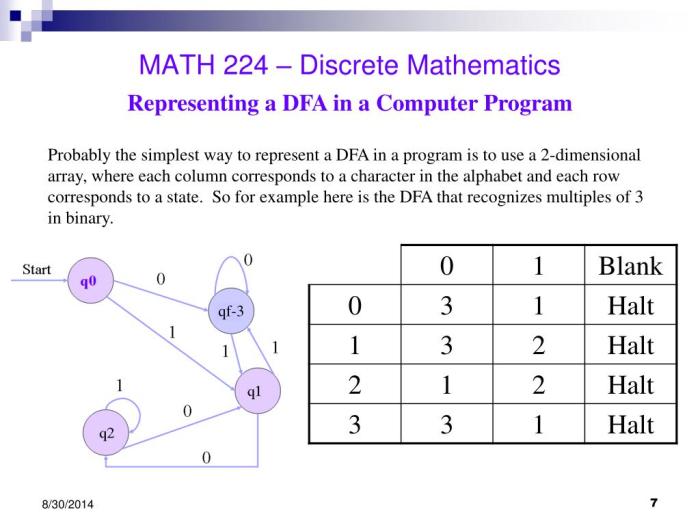
Matematika diskrit adalah cabang matematika yang mempelajari objek-objek diskrit, seperti bilangan bulat, himpunan, dan graf. Objek-objek ini berbeda dengan objek-objek dalam matematika kontinu, seperti bilangan real, fungsi kontinu, dan geometri. Matematika diskrit memiliki banyak aplikasi dalam ilmu komputer, rekayasa, dan ilmu lainnya.
Logika Proposisi
Logika proposisi adalah cabang logika yang mempelajari proposisi dan hubungan antar proposisi. Proposisi adalah pernyataan yang bernilai benar atau salah. Misalnya, “2 + 2 = 4” adalah proposisi yang bernilai benar, sedangkan “2 + 2 = 5” adalah proposisi yang bernilai salah.
Logika proposisi digunakan untuk membangun argumen yang valid. Argumen yang valid adalah argumen yang memiliki kesimpulan yang benar jika semua premisnya benar. Logika proposisi juga digunakan untuk merancang sistem komputer dan jaringan.
- Konjungsi: “p dan q” adalah benar jika dan hanya jika p dan q keduanya benar. Simbol untuk konjungsi adalah ∧.
- Disjungsi: “p atau q” adalah benar jika dan hanya jika p atau q atau keduanya benar. Simbol untuk disjungsi adalah ∨.
- Implikasi: “Jika p, maka q” adalah benar jika dan hanya jika p salah atau q benar. Simbol untuk implikasi adalah →.
- Biimplikasi: “p jika dan hanya jika q” adalah benar jika dan hanya jika p dan q memiliki nilai kebenaran yang sama. Simbol untuk biimplikasi adalah ↔.
Contoh penerapan logika proposisi dalam pembuktian matematika adalah pembuktian teorema dengan menggunakan deduksi logis. Misalnya, untuk membuktikan teorema “Jika p, maka q”, kita dapat menggunakan premis p dan aturan inferensi logika untuk menyimpulkan q.
Himpunan dan Operasi Himpunan
Himpunan adalah kumpulan objek yang berbeda. Objek-objek dalam himpunan disebut elemen. Misalnya, himpunan bilangan bulat positif adalah 1, 2, 3, …. Himpunan dapat ditulis dengan menggunakan tanda kurung kurawal . Himpunan kosong adalah himpunan yang tidak memiliki elemen, ditulis dengan .
Operasi himpunan adalah operasi yang dilakukan pada himpunan. Operasi himpunan yang umum meliputi:
- Gabungan: Gabungan dari dua himpunan adalah himpunan yang berisi semua elemen dari kedua himpunan tersebut. Simbol untuk gabungan adalah ∪.
- Irisan: Irisan dari dua himpunan adalah himpunan yang berisi semua elemen yang sama dari kedua himpunan tersebut. Simbol untuk irisan adalah ∩.
- Selisih: Selisih dari dua himpunan adalah himpunan yang berisi semua elemen dari himpunan pertama yang tidak ada di himpunan kedua. Simbol untuk selisih adalah -.
- Komplemen: Komplemen dari suatu himpunan adalah himpunan yang berisi semua elemen yang tidak ada di himpunan tersebut. Simbol untuk komplemen adalah ¬.
Contoh ilustrasi himpunan dan operasi himpunan adalah himpunan A = 1, 2, 3 dan himpunan B = 2, 3, 4. Gabungan dari A dan B adalah 1, 2, 3, 4. Irisan dari A dan B adalah 2, 3. Selisih dari A dan B adalah 1. Komplemen dari A adalah 4, 5, 6, ….
Relasi dan Fungsi
Relasi adalah hubungan antara dua atau lebih himpunan. Relasi dapat didefinisikan sebagai himpunan pasangan terurut. Misalnya, relasi “lebih besar dari” antara himpunan bilangan bulat positif adalah (1, 2), (1, 3), (2, 3), ….
Fungsi adalah relasi khusus yang menghubungkan setiap elemen dalam himpunan pertama dengan tepat satu elemen dalam himpunan kedua. Misalnya, fungsi “kuadrat” menghubungkan setiap bilangan bulat positif dengan kuadratnya. Fungsi dapat ditulis dengan menggunakan notasi f(x) = y, di mana x adalah elemen dalam himpunan pertama dan y adalah elemen dalam himpunan kedua.
Contoh relasi dan fungsi dalam matematika diskrit adalah relasi “kurang dari” antara himpunan bilangan bulat dan fungsi “faktorial” yang menghubungkan setiap bilangan bulat positif dengan faktorialnya. Faktorial dari suatu bilangan bulat positif n adalah hasil kali dari semua bilangan bulat positif dari 1 hingga n, ditulis dengan n!.
Penerapan Matematika Diskrit dalam Bidang Lain
Matematika diskrit, dengan fokus pada objek-objek terhitung dan struktur diskrit, memiliki peran penting dalam berbagai bidang, khususnya dalam dunia komputer dan teknologi informasi. Penerapannya tidak terbatas pada ilmu komputer, tetapi juga meluas ke bidang lain seperti ekonomi, biologi, dan ilmu sosial.
Penerapan dalam Komputer dan Teknologi Informasi
Matematika diskrit merupakan fondasi dalam pengembangan algoritma, pemrograman, dan keamanan data. Konsep-konsep seperti logika, teori himpunan, dan teori graf menjadi alat penting dalam merancang dan menganalisis algoritma yang efisien. Berikut beberapa contoh penerapannya:
- Algoritma: Algoritma sorting, pencarian, dan kompresi data memanfaatkan konsep-konsep matematika diskrit seperti rekursi, induksi, dan teori graf. Misalnya, algoritma quicksort menggunakan rekursi untuk mengurutkan data dengan membagi data menjadi bagian-bagian yang lebih kecil.
- Pemrograman: Konsep logika dan teori himpunan menjadi dasar dalam bahasa pemrograman, terutama dalam pengembangan program yang berhubungan dengan manipulasi data dan kontrol alur.
- Keamanan Data: Kriptografi, yang merupakan ilmu tentang menjaga kerahasiaan data, menggunakan konsep matematika diskrit seperti teori bilangan dan teori grup. Contohnya, algoritma RSA yang banyak digunakan dalam sistem keamanan online, menggunakan teori bilangan untuk menghasilkan kunci publik dan privat yang sulit dipecahkan.
Penerapan dalam Ilmu Komputer
Matematika diskrit berperan penting dalam memahami dan mengembangkan berbagai konsep dalam ilmu komputer, seperti teori graf, teori automata, dan teori komputasi. Berikut beberapa contoh penerapannya:
- Teori Graf: Teori graf digunakan dalam berbagai aplikasi seperti perencanaan rute, jaringan komputer, dan analisis data. Misalnya, algoritma Dijkstra, yang menggunakan teori graf, dapat digunakan untuk menemukan rute terpendek antara dua titik dalam suatu jaringan.
- Teori Automata: Teori automata digunakan untuk merancang dan menganalisis mesin pencari, compiler, dan sistem kontrol. Contohnya, automata finit dapat digunakan untuk memodelkan mesin pencari yang dapat mengenali pola teks tertentu.
- Teori Komputasi: Teori komputasi mempelajari batasan dan kemampuan komputasi. Konsep-konsep seperti kompleksitas algoritma dan teori Turing menjadi dasar dalam memahami kemampuan dan keterbatasan komputer dalam menyelesaikan masalah.
Penerapan dalam Bidang Lain
Matematika diskrit juga memiliki aplikasi yang luas dalam berbagai bidang lain, seperti ekonomi, biologi, dan ilmu sosial.
- Ekonomi: Teori permainan, yang menggunakan konsep matematika diskrit seperti teori graf dan teori himpunan, digunakan untuk menganalisis perilaku ekonomi dan strategi dalam pasar. Misalnya, teori permainan dapat digunakan untuk memahami bagaimana perusahaan bersaing dalam pasar dan bagaimana konsumen membuat keputusan pembelian.
- Biologi: Konsep-konsep matematika diskrit digunakan dalam biologi untuk memodelkan sistem biologis, seperti jaringan saraf dan interaksi antar spesies. Misalnya, teori graf dapat digunakan untuk memodelkan jaringan interaksi antar spesies dalam suatu ekosistem.
- Ilmu Sosial: Matematika diskrit digunakan dalam ilmu sosial untuk menganalisis data sosial, seperti jaringan sosial dan perilaku kelompok. Misalnya, teori graf dapat digunakan untuk menganalisis jaringan hubungan sosial dan bagaimana informasi menyebar dalam suatu kelompok.
Contoh Soal dan Penyelesaian Matematika Diskrit
Matematika diskrit merupakan cabang matematika yang mempelajari objek-objek diskrit, seperti bilangan bulat, himpunan, grafik, dan algoritma. Materi ini memiliki banyak aplikasi dalam bidang komputer, ekonomi, biologi, dan lainnya. Berikut adalah contoh soal matematika diskrit beserta penyelesaiannya untuk memperjelas pemahaman.
Logika Proposisi
Logika proposisi adalah cabang logika yang mempelajari pernyataan-pernyataan yang dapat diuji kebenarannya. Pernyataan-pernyataan tersebut disebut proposisi. Contoh soal logika proposisi:
- Tentukan nilai kebenaran dari proposisi berikut: “Jika hari ini hujan, maka saya akan membawa payung.”
Penyelesaian:
- Proposisi ini merupakan implikasi, yaitu proposisi yang menyatakan “Jika p, maka q”.
- Dalam kasus ini, p = “hari ini hujan” dan q = “saya akan membawa payung”.
- Implikasi hanya bernilai salah jika p benar dan q salah.
- Oleh karena itu, jika hari ini hujan (p benar) dan saya tidak membawa payung (q salah), maka proposisi tersebut bernilai salah.
- Jika hari ini hujan (p benar) dan saya membawa payung (q benar), maka proposisi tersebut bernilai benar.
- Jika hari ini tidak hujan (p salah), maka proposisi tersebut bernilai benar, terlepas dari apakah saya membawa payung atau tidak.
Himpunan
Himpunan adalah kumpulan objek yang terdefinisi dengan baik. Contoh soal himpunan:
- Diberikan himpunan A = 1, 2, 3, 4 dan himpunan B = 3, 4, 5, 6. Tentukan:
- A ∪ B (gabungan dari A dan B)
- A ∩ B (irisan dari A dan B)
- A – B (selisih dari A dan B)
Penyelesaian:
- A ∪ B = 1, 2, 3, 4, 5, 6
- A ∩ B = 3, 4
- A – B = 1, 2
Relasi
Relasi adalah hubungan antara elemen-elemen dari dua himpunan. Contoh soal relasi:
- Diberikan himpunan A = 1, 2, 3 dan himpunan B = a, b, c. Relasi R dari A ke B didefinisikan sebagai berikut: R = (1, a), (2, b), (3, c). Tentukan:
- Domain dari R
- Kodomain dari R
- Range dari R
Penyelesaian:
- Domain dari R adalah 1, 2, 3, yaitu himpunan semua elemen pertama dari pasangan-pasangan dalam R.
- Kodomain dari R adalah a, b, c, yaitu himpunan semua elemen kedua dari pasangan-pasangan dalam R.
- Range dari R adalah a, b, c, yaitu himpunan semua elemen kedua dari pasangan-pasangan dalam R yang memiliki elemen pertama di domain R.
Fungsi
Fungsi adalah relasi khusus yang memasangkan setiap elemen dalam domain dengan tepat satu elemen dalam kodomain. Contoh soal fungsi:
- Diberikan fungsi f(x) = x2 + 1. Tentukan:
- Nilai f(2)
- Nilai f(-1)
Penyelesaian:
- f(2) = 22 + 1 = 5
- f(-1) = (-1)2 + 1 = 2
Penerapan Matematika Diskrit
Matematika diskrit memiliki banyak aplikasi dalam bidang lain, seperti komputer, ekonomi, dan biologi. Berikut adalah contoh soal yang melibatkan penerapan matematika diskrit:
- Dalam ilmu komputer, algoritma merupakan serangkaian langkah yang terdefinisi dengan baik untuk menyelesaikan masalah tertentu. Contohnya, algoritma pencarian linear digunakan untuk menemukan suatu elemen dalam sebuah daftar. Algoritma ini menggunakan konsep himpunan dan relasi untuk mendefinisikan langkah-langkahnya.
- Dalam ekonomi, teori permainan menggunakan konsep logika proposisi dan teori himpunan untuk menganalisis perilaku pemain dalam situasi strategis. Contohnya, dalam permainan “Dilema Narapidana”, setiap pemain harus memilih antara bekerja sama atau berkhianat. Hasil dari permainan bergantung pada pilihan kedua pemain, dan teori permainan dapat digunakan untuk memprediksi hasil yang paling mungkin.
- Dalam biologi, matematika diskrit digunakan untuk memodelkan sistem biologi, seperti jaringan saraf dan populasi sel. Contohnya, model SIR digunakan untuk memodelkan penyebaran penyakit menular. Model ini menggunakan konsep fungsi dan relasi untuk mendefinisikan interaksi antara individu yang sehat, terinfeksi, dan pulih.
Penutup

Memahami matematika diskrit membuka pintu bagi kita untuk menjelajahi dunia yang terstruktur dan terhitung. Dari menguraikan algoritma komputer hingga memahami pola dalam sistem kompleks, matematika diskrit memberikan alat yang kuat untuk menganalisis, memecahkan masalah, dan membangun solusi inovatif di berbagai bidang.







