Soal matematika integral – Integral, konsep matematika yang mungkin terdengar asing bagi sebagian orang, ternyata memegang peranan penting dalam berbagai bidang ilmu. Bayangkan, integral bisa digunakan untuk menghitung luas area yang rumit, volume benda tiga dimensi, bahkan untuk menganalisis pergerakan benda. Mempelajari integral membuka pintu menuju pemahaman yang lebih dalam tentang dunia di sekitar kita.
Soal matematika integral, yang menguji pemahaman kita tentang konsep integral, seringkali muncul dalam berbagai ujian dan kompetisi. Artikel ini akan membahas secara mendalam tentang soal matematika integral, mulai dari definisi dasar hingga aplikasi praktisnya dalam berbagai bidang.
Pengertian Integral: Soal Matematika Integral
Integral merupakan konsep fundamental dalam matematika yang berkaitan dengan penjumlahan luas daerah di bawah kurva suatu fungsi. Integral merupakan operasi kebalikan dari diferensial, dan sering digunakan dalam berbagai bidang seperti fisika, teknik, ekonomi, dan statistika.
Konsep Integral
Integral dapat dibayangkan sebagai penjumlahan luas daerah yang terkurung di antara kurva suatu fungsi, sumbu x, dan dua garis vertikal. Dalam konteks ini, integral merupakan generalisasi dari konsep luas persegi panjang, yang dapat dihitung dengan mengalikan panjang dan lebarnya.
Contoh Soal Integral Sederhana
Misalkan kita ingin mencari luas daerah yang terkurung di antara kurva fungsi f(x) = x^2, sumbu x, dan garis vertikal x = 0 dan x = 2.
Langkah penyelesaiannya adalah sebagai berikut:
- Tentukan fungsi f(x) yang akan diintegralkan, dalam hal ini f(x) = x^2.
- Tentukan batas bawah dan batas atas integrasi, dalam hal ini x = 0 dan x = 2.
- Hitung integral tentu dari fungsi f(x) dengan batas bawah dan batas atas yang telah ditentukan.
Integral tentu dari f(x) = x^2 dengan batas bawah 0 dan batas atas 2 adalah:
∫02 x2 dx = [x3/3]02 = (23/3) – (03/3) = 8/3.
Jadi, luas daerah yang terkurung di antara kurva fungsi f(x) = x^2, sumbu x, dan garis vertikal x = 0 dan x = 2 adalah 8/3 satuan luas.
Perbedaan Integral Tak Tentu dan Integral Tentu
| Fitur | Integral Tak Tentu | Integral Tentu |
|---|---|---|
| Definisi | Suatu keluarga fungsi yang turunannya sama dengan fungsi yang diintegralkan. | Nilai tunggal yang merepresentasikan luas daerah di bawah kurva fungsi dalam interval tertentu. |
| Batas Integrasi | Tidak memiliki batas integrasi. | Memiliki batas integrasi bawah dan atas. |
| Hasil | Fungsi dengan konstanta integrasi. | Nilai numerik. |
| Aplikasi | Mencari fungsi primitif, menyelesaikan persamaan diferensial. | Menghitung luas daerah, volume, dan besaran fisika lainnya. |
Ilustrasi Konsep Integral
Bayangkan sebuah kurva fungsi yang terletak di atas sumbu x. Integral dari fungsi tersebut dapat diartikan sebagai penjumlahan luas semua persegi panjang kecil yang terletak di bawah kurva, dengan lebar setiap persegi panjang mendekati nol. Semakin banyak persegi panjang yang kita gunakan, semakin akurat hasil perhitungan integral.
Secara visual, kita dapat membayangkan integral sebagai penjumlahan luas daerah yang terkurung di antara kurva fungsi, sumbu x, dan dua garis vertikal yang menandai batas integrasi. Luas daerah ini dibagi menjadi sejumlah persegi panjang kecil, dan integral adalah limit penjumlahan luas semua persegi panjang kecil tersebut ketika lebar setiap persegi panjang mendekati nol.
Jenis-jenis Integral
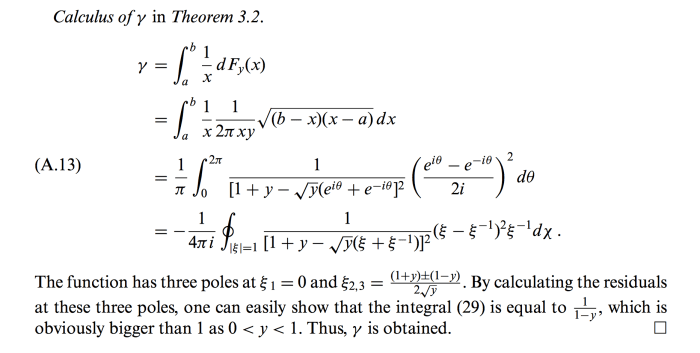
Integral merupakan konsep fundamental dalam kalkulus yang memungkinkan kita untuk menghitung luas area di bawah kurva, volume benda putar, dan banyak aplikasi lainnya. Dalam matematika, integral dibagi menjadi beberapa jenis, masing-masing memiliki metode penyelesaian dan aplikasi yang berbeda.
Integral Tak Tentu
Integral tak tentu adalah fungsi yang turunannya sama dengan fungsi yang diberikan. Integral tak tentu merupakan konsep dasar dalam kalkulus dan sering digunakan untuk mencari antiturunan dari fungsi. Integral tak tentu dilambangkan dengan simbol ∫.
Contoh: Integral tak tentu dari f(x) = x2 adalah F(x) = (1/3)x3 + C, dimana C adalah konstanta integrasi.
Integral Tentu
Integral tentu adalah nilai integral yang dihitung pada batas atas dan batas bawah tertentu. Integral tentu sering digunakan untuk menghitung luas area di bawah kurva, volume benda putar, dan banyak aplikasi lainnya. Integral tentu dilambangkan dengan simbol ∫ab.
Contoh: Integral tentu dari f(x) = x2 dari x = 0 sampai x = 2 adalah ∫02 x2 dx = (1/3)x3 |02 = (1/3)(2)3 – (1/3)(0)3 = 8/3.
Integral Substitusi
Integral substitusi adalah teknik integrasi yang digunakan untuk menyederhanakan integral dengan mengganti variabel dalam integral dengan variabel baru. Metode ini sangat berguna untuk menyelesaikan integral yang rumit, terutama ketika integran mengandung fungsi komposit.
Integral Parsial
Integral parsial adalah teknik integrasi yang digunakan untuk menyelesaikan integral yang melibatkan perkalian dua fungsi. Metode ini didasarkan pada aturan perkalian dalam turunan. Integral parsial sering digunakan untuk menyelesaikan integral yang melibatkan fungsi trigonometri, eksponensial, dan logaritma.
Perbedaan Integral Substitusi dan Integral Parsial
Integral substitusi dan integral parsial adalah dua teknik integrasi yang berbeda, tetapi keduanya bertujuan untuk menyederhanakan integral. Perbedaan utama antara keduanya adalah:
- Integral substitusi digunakan untuk menyederhanakan integral dengan mengganti variabel dalam integral dengan variabel baru, sedangkan integral parsial digunakan untuk menyelesaikan integral yang melibatkan perkalian dua fungsi.
- Integral substitusi biasanya digunakan ketika integran mengandung fungsi komposit, sedangkan integral parsial biasanya digunakan ketika integran mengandung perkalian dua fungsi yang tidak dapat disederhanakan dengan substitusi.
Rumus-Rumus Integral Dasar
| Fungsi | Integral |
|---|---|
| xn | (1/(n+1))xn+1 + C |
| sin(x) | -cos(x) + C |
| cos(x) | sin(x) + C |
| ex | ex + C |
| 1/x | ln(|x|) + C |
Contoh Penyelesaian Integral dengan Metode Integrasi Parsial
Misalkan kita ingin menyelesaikan integral ∫ x sin(x) dx. Kita dapat menggunakan metode integrasi parsial dengan langkah-langkah berikut:
- Pilih u = x dan dv = sin(x) dx.
- Hitung du = dx dan v = -cos(x).
- Gunakan rumus integrasi parsial: ∫ u dv = uv – ∫ v du.
- Substitusikan nilai u, dv, du, dan v ke dalam rumus integrasi parsial:
- Selesaikan integral ∫ -cos(x) dx = sin(x) + C.
- Substitusikan nilai ∫ -cos(x) dx ke dalam persamaan sebelumnya:
∫ x sin(x) dx = -x cos(x) – ∫ -cos(x) dx.
∫ x sin(x) dx = -x cos(x) + sin(x) + C.
Aplikasi Integral
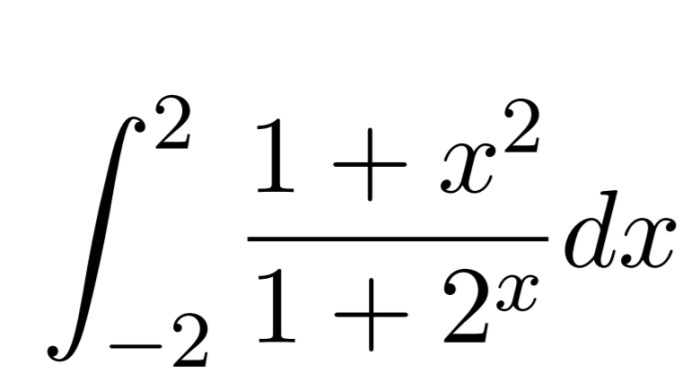
Integral merupakan konsep penting dalam matematika yang memiliki aplikasi luas di berbagai bidang ilmu, seperti fisika, ekonomi, dan teknik. Konsep integral memungkinkan kita untuk menghitung luas daerah, volume benda, dan banyak besaran lain yang tidak dapat dihitung dengan menggunakan kalkulus diferensial saja.
Aplikasi Integral dalam Berbagai Bidang Ilmu
Berikut adalah beberapa contoh aplikasi integral dalam berbagai bidang ilmu:
- Fisika: Integral digunakan untuk menghitung kerja yang dilakukan oleh gaya, energi potensial, momen inersia, dan banyak lagi. Misalnya, untuk menghitung kerja yang dilakukan oleh gaya konstan pada benda yang bergerak sepanjang lintasan tertentu, kita dapat menggunakan integral. Kerja yang dilakukan oleh gaya tersebut adalah hasil kali gaya dengan perpindahan benda, dan integral digunakan untuk menghitung perpindahan total.
- Ekonomi: Integral digunakan untuk menghitung total pendapatan, total biaya, dan total keuntungan dari suatu perusahaan. Misalnya, untuk menghitung total pendapatan dari menjual produk tertentu, kita dapat menggunakan integral untuk menghitung luas daerah di bawah kurva permintaan.
- Teknik: Integral digunakan untuk menghitung volume benda, luas permukaan, dan pusat massa. Misalnya, untuk menghitung volume benda putar, kita dapat menggunakan integral untuk menghitung volume irisan tipis benda tersebut dan kemudian menjumlahkannya.
Contoh Soal Integral Menghitung Volume Benda Putar
Misalnya, kita ingin menghitung volume benda putar yang dihasilkan dengan memutar kurva y = x2 di sekitar sumbu x pada interval 0 ≤ x ≤ 2.
Untuk menghitung volume benda putar, kita dapat menggunakan metode cakram. Metode cakram melibatkan pembagian benda putar menjadi irisan tipis berbentuk cakram, dengan jari-jari r dan ketebalan dx. Volume setiap cakram adalah πr2dx, dan volume total benda putar adalah hasil integral dari volume setiap cakram.
Dalam kasus ini, jari-jari cakram adalah r = y = x2, dan ketebalan cakram adalah dx. Oleh karena itu, volume benda putar adalah:
V = ∫02 π(x2)2 dx = π∫02 x4 dx = π[x5/5]02 = (32/5)π
Jadi, volume benda putar yang dihasilkan dengan memutar kurva y = x2 di sekitar sumbu x pada interval 0 ≤ x ≤ 2 adalah (32/5)π.
Contoh Soal Integral Menghitung Luas Daerah yang Dibatasi oleh Beberapa Kurva
Misalnya, kita ingin menghitung luas daerah yang dibatasi oleh kurva y = x2 dan y = 2x.
Untuk menghitung luas daerah, kita dapat menggunakan integral. Integral digunakan untuk menghitung luas daerah di bawah kurva, dan luas daerah yang dibatasi oleh beberapa kurva dapat dihitung dengan mengurangkan luas daerah di bawah kurva yang lebih tinggi dari luas daerah di bawah kurva yang lebih rendah.
Dalam kasus ini, kurva y = 2x terletak di atas kurva y = x2 pada interval 0 ≤ x ≤ 2. Oleh karena itu, luas daerah yang dibatasi oleh kedua kurva adalah:
A = ∫02 (2x – x2) dx = [x2 – x3/3]02 = (4/3)
Jadi, luas daerah yang dibatasi oleh kurva y = x2 dan y = 2x adalah (4/3).
Aplikasi Integral dalam Menghitung Kecepatan dan Jarak
Integral dapat digunakan untuk menghitung kecepatan dan jarak suatu benda yang bergerak dengan kecepatan yang berubah-ubah.
Misalnya, jika kita mengetahui fungsi kecepatan v(t) dari suatu benda, kita dapat menggunakan integral untuk menghitung jarak yang ditempuh benda tersebut pada interval waktu tertentu. Jarak yang ditempuh benda adalah hasil integral dari kecepatan benda terhadap waktu.
Contohnya, jika kecepatan suatu benda diberikan oleh fungsi v(t) = 2t, maka jarak yang ditempuh benda pada interval waktu 0 ≤ t ≤ 3 adalah:
s = ∫03 2t dt = [t2]03 = 9
Jadi, jarak yang ditempuh benda pada interval waktu 0 ≤ t ≤ 3 adalah 9 satuan.
Demikian pula, jika kita mengetahui fungsi percepatan a(t) dari suatu benda, kita dapat menggunakan integral untuk menghitung kecepatan benda pada interval waktu tertentu. Kecepatan benda adalah hasil integral dari percepatan benda terhadap waktu.
Contohnya, jika percepatan suatu benda diberikan oleh fungsi a(t) = 2, maka kecepatan benda pada interval waktu 0 ≤ t ≤ 3 adalah:
v = ∫03 2 dt = [2t]03 = 6
Jadi, kecepatan benda pada interval waktu 0 ≤ t ≤ 3 adalah 6 satuan per satuan waktu.
Teknik Integrasi
Integrasi merupakan salah satu konsep penting dalam kalkulus. Integrasi merupakan operasi invers dari diferensiasi, yang berarti mencari fungsi yang turunannya adalah fungsi yang diberikan. Teknik integrasi merupakan kumpulan metode dan strategi untuk mencari solusi integral dari berbagai jenis fungsi.
Integrasi Parsial
Integrasi parsial merupakan teknik yang digunakan untuk mengintegrasikan hasil kali dua fungsi. Teknik ini didasarkan pada aturan turunan hasil kali dua fungsi.
∫ u dv = uv – ∫ v du
Dimana u dan v adalah fungsi yang dapat diturunkan.
Untuk menggunakan integrasi parsial, langkah-langkahnya adalah sebagai berikut:
- Tentukan fungsi u dan dv.
- Hitung du dan v.
- Gunakan rumus integrasi parsial untuk mencari integral.
- Selesaikan integral yang tersisa.
Integrasi Substitusi, Soal matematika integral
Integrasi substitusi merupakan teknik yang digunakan untuk menyederhanakan integral dengan mengganti variabel integral dengan variabel baru. Teknik ini didasarkan pada aturan rantai diferensiasi.
Untuk menggunakan integrasi substitusi, langkah-langkahnya adalah sebagai berikut:
- Tentukan substitusi yang sesuai.
- Hitung turunan dari substitusi.
- Ganti variabel integral dan diferensialnya dengan substitusi dan turunannya.
- Selesaikan integral yang tersisa.
- Ganti kembali variabel integral dengan substitusi.
Berikut contoh soal integral yang dipecahkan menggunakan metode integrasi substitusi:
∫ 2x(x^2 + 1)^3 dx
Misalkan u = x^2 + 1, maka du = 2x dx. Dengan substitusi ini, integral tersebut dapat diubah menjadi:
∫ u^3 du
Integral ini dapat diselesaikan dengan mudah menggunakan aturan pangkat:
∫ u^3 du = (1/4)u^4 + C
Ganti kembali u dengan x^2 + 1, maka solusi integralnya adalah:
(1/4)(x^2 + 1)^4 + C
Integrasi Trigonometri
Integrasi trigonometri merupakan teknik yang digunakan untuk mengintegrasikan fungsi trigonometri. Teknik ini didasarkan pada identitas trigonometri.
Berikut contoh soal integral yang dipecahkan menggunakan metode integrasi parsial:
∫ x sin(x) dx
Misalkan u = x dan dv = sin(x) dx, maka du = dx dan v = -cos(x). Dengan integrasi parsial, integral tersebut dapat diubah menjadi:
-x cos(x) + ∫ cos(x) dx
Integral yang tersisa dapat diselesaikan dengan mudah:
-x cos(x) + sin(x) + C
Tabel Langkah-langkah Integrasi Parsial
| Langkah | Keterangan |
|---|---|
| 1. Tentukan fungsi u dan dv. | Pilih fungsi u yang dapat diturunkan dan fungsi dv yang dapat diintegralkan. |
| 2. Hitung du dan v. | Hitung turunan dari u dan integral dari dv. |
| 3. Gunakan rumus integrasi parsial. | Gunakan rumus ∫ u dv = uv – ∫ v du. |
| 4. Selesaikan integral yang tersisa. | Selesaikan integral yang tersisa menggunakan teknik integrasi yang sesuai. |
Penerapan Integral dalam Soal Matematika
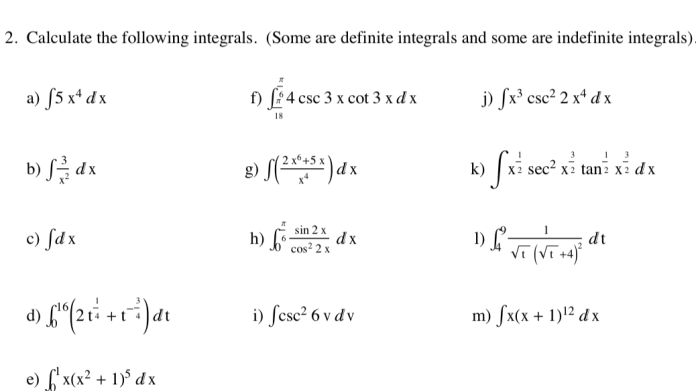
Integral merupakan konsep fundamental dalam matematika yang memiliki aplikasi luas dalam berbagai bidang, mulai dari fisika dan teknik hingga ekonomi dan statistika. Penerapan integral memungkinkan kita untuk menghitung luas, volume, dan berbagai besaran lain yang melibatkan konsep kontinuitas.
Contoh Soal Integral Tentu dan Integral Tak Tentu
Integral tentu dan integral tak tentu merupakan dua konsep penting dalam kalkulus integral. Integral tentu digunakan untuk menghitung luas daerah di bawah kurva, sedangkan integral tak tentu digunakan untuk mencari fungsi primitif dari suatu fungsi.
- Contoh Soal Integral Tentu: Hitung luas daerah yang dibatasi oleh kurva y = x2, sumbu x, garis x = 1, dan garis x = 2.
- Contoh Soal Integral Tak Tentu: Tentukan integral tak tentu dari fungsi f(x) = 2x + 3.
Contoh Soal Integral dalam Menghitung Volume Benda Putar
Integral dapat digunakan untuk menghitung volume benda putar yang dihasilkan ketika suatu kurva diputar mengelilingi sumbu tertentu. Metode ini melibatkan penggunaan integral tentu untuk menghitung luas penampang melintang benda putar pada setiap titik dan kemudian mengintegrasikan luas tersebut terhadap sumbu putar.
- Contoh Soal: Tentukan volume benda putar yang dihasilkan ketika kurva y = x2 diputar mengelilingi sumbu x pada interval x = 0 hingga x = 2.
Contoh Soal Integral yang Melibatkan Konsep Turunan dan Integral
Turunan dan integral merupakan konsep yang saling terkait dalam kalkulus. Turunan dari suatu fungsi memberikan kemiringan garis singgung pada titik tertentu pada kurva, sedangkan integral dari suatu fungsi memberikan luas daerah di bawah kurva.
- Contoh Soal: Jika f'(x) = 2x + 1 dan f(0) = 2, tentukan fungsi f(x).
Langkah-langkah Menyelesaikan Soal Matematika Integral
| Langkah | Penjelasan |
|---|---|
| 1. Pahami konsep integral yang terlibat. | Identifikasi jenis integral yang digunakan dalam soal, baik integral tentu, integral tak tentu, atau integral ganda. |
| 2. Tentukan batas integrasi. | Jika soal melibatkan integral tentu, tentukan batas atas dan batas bawah integrasi. |
| 3. Tentukan fungsi integran. | Identifikasi fungsi yang akan diintegrasikan. |
| 4. Selesaikan integral. | Gunakan aturan-aturan integrasi yang sesuai untuk menyelesaikan integral. |
| 5. Evaluasi integral. | Jika soal melibatkan integral tentu, evaluasi hasil integral pada batas integrasi. |
Penutup
Memahami soal matematika integral tidak hanya penting untuk meraih nilai bagus dalam ujian, tetapi juga untuk membuka cakrawala berpikir kita dalam memecahkan masalah kompleks di berbagai bidang. Dengan memahami konsep integral, kita dapat melihat dunia dengan perspektif yang lebih luas dan menemukan solusi inovatif untuk berbagai tantangan.






