Menjelang ujian akhir, pasti kamu sedang giat-giatnya belajar matematika kelas 12, kan? Nah, untuk membantu kamu menguasai materi dan meningkatkan kemampuan memecahkan soal, artikel ini akan membahas soal dan jawaban matematika kelas 12, mulai dari materi turunan fungsi hingga aplikasi matematika dalam kehidupan sehari-hari.
Tidak hanya sekadar contoh soal dan jawaban, artikel ini juga akan membahas strategi jitu untuk menyelesaikan soal-soal matematika yang menantang. Kamu juga akan menemukan tips dan trik untuk memahami konsep-konsep matematika yang sulit, serta contoh soal dan jawaban yang menguji kemampuan berpikir kritis dan analitis.
Matematika Kelas 12: Menjelajahi Konsep-Konsep Penting: Soal Dan Jawaban Matematika Kelas 12
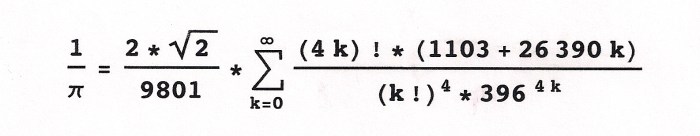
Matematika kelas 12 merupakan tahap lanjutan dari pembelajaran matematika yang menitikberatkan pada konsep-konsep abstrak dan aplikasinya dalam berbagai bidang. Beberapa materi penting yang dipelajari di kelas ini meliputi turunan fungsi, integral tentu, limit fungsi, vektor, dan matriks. Materi-materi ini memiliki peranan penting dalam berbagai bidang ilmu pengetahuan dan teknologi, sehingga penguasaan yang baik atas materi-materi tersebut sangatlah penting.
Turunan Fungsi
Turunan fungsi merupakan salah satu konsep dasar dalam kalkulus yang mengkaji tentang laju perubahan suatu fungsi. Konsep turunan memiliki aplikasi yang luas dalam berbagai bidang, seperti fisika, ekonomi, dan teknik.
Berikut adalah contoh soal dan jawaban tentang turunan fungsi:
Diketahui fungsi f(x) = x2 + 2x – 3. Tentukan turunan dari fungsi f(x).
Penyelesaian:
Turunan dari fungsi f(x) = x2 + 2x – 3 dapat dihitung dengan menggunakan aturan turunan dasar, yaitu:
- Turunan dari xn = n.xn-1
- Turunan dari konstanta = 0
Dengan menggunakan aturan tersebut, maka turunan dari f(x) adalah:
f'(x) = 2x + 2
Integral Tentu
Integral tentu merupakan konsep dalam kalkulus yang mengkaji tentang luas daerah yang dibatasi oleh kurva, sumbu x, dan garis vertikal. Integral tentu memiliki aplikasi luas dalam berbagai bidang, seperti fisika, ekonomi, dan teknik.
Berikut adalah contoh soal dan jawaban tentang integral tentu:
Hitunglah integral tentu dari fungsi f(x) = x2 + 1 pada interval [0, 2].
Penyelesaian:
Integral tentu dari fungsi f(x) = x2 + 1 pada interval [0, 2] dapat dihitung dengan menggunakan rumus integral tentu, yaitu:
∫ab f(x) dx = F(b) – F(a)
Dimana F(x) adalah antiturunan dari f(x).
Antiturunan dari f(x) = x2 + 1 adalah F(x) = (1/3)x3 + x.
Maka, integral tentu dari f(x) = x2 + 1 pada interval [0, 2] adalah:
∫02 (x2 + 1) dx = F(2) – F(0) = ((1/3)23 + 2) – ((1/3)03 + 0) = (8/3 + 2) – 0 = 14/3
Limit Fungsi
Limit fungsi merupakan konsep dasar dalam kalkulus yang mengkaji tentang nilai fungsi ketika variabel mendekati suatu nilai tertentu. Konsep limit memiliki aplikasi yang luas dalam berbagai bidang, seperti fisika, ekonomi, dan teknik.
Berikut adalah contoh soal dan jawaban tentang limit fungsi:
Tentukan limit dari fungsi f(x) = (x2 – 1)/(x – 1) ketika x mendekati 1.
Penyelesaian:
Limit dari fungsi f(x) = (x2 – 1)/(x – 1) ketika x mendekati 1 dapat dihitung dengan menggunakan metode substitusi.
Namun, jika kita substitusikan x = 1 ke dalam fungsi f(x), maka akan menghasilkan bentuk tak tentu 0/0.
Untuk mengatasi hal ini, kita dapat memfaktorkan fungsi f(x) terlebih dahulu, yaitu:
f(x) = (x2 – 1)/(x – 1) = (x + 1)(x – 1)/(x – 1) = x + 1
Setelah difaktorkan, kita dapat substitusikan x = 1 ke dalam fungsi f(x), sehingga diperoleh:
limx→1 f(x) = limx→1 (x + 1) = 1 + 1 = 2
Vektor
Vektor merupakan besaran yang memiliki nilai dan arah. Vektor memiliki aplikasi yang luas dalam berbagai bidang, seperti fisika, teknik, dan komputer grafis.
Berikut adalah contoh soal dan jawaban tentang vektor:
Diketahui vektor a = (2, 3) dan b = (1, -1). Tentukan hasil penjumlahan vektor a dan b.
Penyelesaian:
Penjumlahan vektor dilakukan dengan menjumlahkan komponen-komponen yang bersesuaian.
Maka, hasil penjumlahan vektor a dan b adalah:
a + b = (2, 3) + (1, -1) = (2 + 1, 3 – 1) = (3, 2)
Matriks
Matriks merupakan susunan bilangan yang disusun dalam baris dan kolom. Matriks memiliki aplikasi yang luas dalam berbagai bidang, seperti fisika, ekonomi, dan komputer grafis.
Berikut adalah contoh soal dan jawaban tentang matriks:
Diketahui matriks A = [2 1; 3 4] dan B = [1 0; -1 2]. Tentukan hasil perkalian matriks A dan B.
Penyelesaian:
Perkalian matriks dilakukan dengan mengalikan setiap elemen baris pada matriks pertama dengan setiap elemen kolom pada matriks kedua, kemudian dijumlahkan.
Maka, hasil perkalian matriks A dan B adalah:
A.B = [2 1; 3 4]. [1 0; -1 2] = [(2.1 + 1.(-1)) (2.0 + 1.2); (3.1 + 4.(-1)) (3.0 + 4.2)] = [1 2; -1 8]
Strategi Menyelesaikan Soal Matematika
Matematika di kelas 12 merupakan mata pelajaran yang membutuhkan pemahaman konsep yang kuat dan kemampuan untuk menerapkannya dalam berbagai situasi. Untuk meraih kesuksesan dalam menghadapi soal-soal matematika kelas 12, penting untuk memiliki strategi yang efektif. Artikel ini akan membahas beberapa strategi yang dapat membantu Anda dalam menyelesaikan soal-soal matematika kelas 12 dengan lebih mudah dan tepat.
Langkah-Langkah Menyelesaikan Soal Cerita Matematika
Soal cerita matematika mengharuskan Anda untuk memahami konteks masalah dan menerjemahkannya ke dalam bahasa matematika. Berikut langkah-langkah yang dapat membantu Anda menyelesaikan soal cerita matematika kelas 12:
| Langkah | Penjelasan |
|---|---|
| 1. Memahami Masalah | Baca soal dengan cermat dan pahami konteksnya. Identifikasi informasi yang diberikan dan apa yang ingin diketahui. |
| 2. Mendefinisikan Variabel | Tentukan variabel yang akan digunakan untuk mewakili besaran yang tidak diketahui dalam soal. |
| 3. Menulis Persamaan | Terjemahkan informasi yang diberikan dalam soal ke dalam bentuk persamaan matematika. |
| 4. Menyelesaikan Persamaan | Selesaikan persamaan yang telah Anda buat untuk mencari nilai variabel yang tidak diketahui. |
| 5. Menginterpretasikan Hasil | Pastikan hasil yang Anda peroleh sesuai dengan konteks soal dan menjawab pertanyaan yang diajukan. |
Strategi Menyelesaikan Soal Kalkulus
Kalkulus merupakan cabang matematika yang mempelajari tentang perubahan dan gerakan. Soal-soal kalkulus biasanya melibatkan konsep seperti turunan, integral, dan limit. Berikut strategi yang dapat membantu Anda menyelesaikan soal kalkulus:
- Pahami Konsep Dasar: Pastikan Anda memahami konsep dasar kalkulus seperti turunan, integral, dan limit. Tanpa pemahaman yang kuat, akan sulit untuk menyelesaikan soal-soal yang lebih kompleks.
- Latih Soal-Soal: Latihlah sebanyak mungkin soal kalkulus untuk mengasah kemampuan Anda dalam menerapkan konsep-konsep yang telah Anda pelajari.
- Gunakan Rumus dan Teorema: Rumus dan teorema dalam kalkulus dapat membantu Anda menyelesaikan soal dengan lebih cepat dan efisien. Pastikan Anda memahami cara menggunakannya dengan tepat.
- Visualisasi Masalah: Visualisasi masalah dapat membantu Anda memahami konteks soal dan menemukan solusi yang tepat. Anda dapat menggunakan grafik atau diagram untuk memvisualisasikan masalah.
Contoh Soal dan Jawaban Penalaran Logis
Soal-soal matematika yang memerlukan penalaran logis biasanya melibatkan pola, deduksi, dan induksi. Berikut contoh soal dan jawabannya:
Jika semua kucing adalah mamalia, dan semua mamalia adalah hewan, maka semua kucing adalah hewan.
Contoh di atas menunjukkan penggunaan deduksi untuk menarik kesimpulan berdasarkan premis yang benar. Soal-soal penalaran logis biasanya membutuhkan kemampuan untuk menganalisis informasi, mengidentifikasi pola, dan menarik kesimpulan yang logis.
Tips dan Trik Memahami Konsep Matematika yang Sulit
Ada beberapa tips dan trik yang dapat membantu Anda memahami konsep-konsep matematika yang sulit:
- Pecah Masalah Menjadi Bagian-Bagian yang Lebih Kecil: Jika Anda menghadapi masalah yang sulit, cobalah untuk memecahnya menjadi bagian-bagian yang lebih kecil dan lebih mudah dipahami.
- Gunakan Contoh: Contoh dapat membantu Anda memahami konsep matematika yang sulit. Cobalah untuk mencari contoh yang relevan dengan konsep yang sedang Anda pelajari.
- Berlatih Secara Teratur: Latihlah secara teratur untuk mengasah kemampuan Anda dalam menyelesaikan soal-soal matematika. Semakin banyak Anda berlatih, semakin mudah Anda akan memahami konsep-konsep yang sulit.
- Mintalah Bantuan: Jangan ragu untuk meminta bantuan dari guru, teman, atau tutor jika Anda kesulitan memahami suatu konsep. Mereka dapat memberikan penjelasan yang lebih mudah dipahami.
Strategi Menyelesaikan Soal Geometri
Soal-soal geometri biasanya melibatkan bentuk, ukuran, dan posisi objek. Berikut strategi yang dapat membantu Anda menyelesaikan soal geometri:
- Mengenal Bentuk Geometri: Pastikan Anda mengenal berbagai bentuk geometri seperti segitiga, persegi panjang, lingkaran, kubus, dan bola.
- Menerapkan Rumus: Rumus-rumus geometri dapat membantu Anda menyelesaikan soal dengan lebih cepat dan efisien. Pastikan Anda memahami cara menggunakannya dengan tepat.
- Menggunakan Diagram: Diagram dapat membantu Anda memvisualisasikan masalah dan menemukan solusi yang tepat. Gunakan diagram untuk menggambarkan bentuk geometri yang diberikan dalam soal.
- Menghubungkan Konsep: Konsep-konsep geometri saling berhubungan. Cobalah untuk menghubungkan konsep-konsep yang telah Anda pelajari untuk menyelesaikan soal dengan lebih mudah.
Aplikasi Matematika dalam Kehidupan Sehari-hari
Matematika, yang sering dianggap sebagai disiplin ilmu abstrak, memiliki aplikasi yang luas dan mendalam dalam kehidupan sehari-hari. Konsep-konsep matematika, dari yang sederhana hingga yang kompleks, berperan penting dalam berbagai bidang, membentuk dan memengaruhi cara kita memahami dan berinteraksi dengan dunia di sekitar kita.
Konsep Turunan Fungsi dalam Ilmu Ekonomi
Konsep turunan fungsi, yang mengukur laju perubahan suatu fungsi terhadap variabelnya, memiliki peran penting dalam ilmu ekonomi. Turunan digunakan untuk menganalisis hubungan antara berbagai variabel ekonomi, seperti penawaran dan permintaan, biaya dan keuntungan, serta pertumbuhan ekonomi.
- Analisis Elastisitas: Turunan digunakan untuk menentukan elastisitas permintaan, yaitu sensitivitas perubahan permintaan terhadap perubahan harga. Elastisitas permintaan yang tinggi menunjukkan bahwa perubahan harga kecil akan menyebabkan perubahan permintaan yang signifikan, sedangkan elastisitas permintaan yang rendah menunjukkan bahwa perubahan harga hanya menyebabkan perubahan permintaan yang kecil.
- Analisis Marginal: Turunan digunakan untuk menentukan biaya marginal, keuntungan marginal, dan pendapatan marginal. Biaya marginal adalah perubahan biaya total akibat peningkatan produksi satu unit, keuntungan marginal adalah perubahan keuntungan total akibat peningkatan penjualan satu unit, dan pendapatan marginal adalah perubahan pendapatan total akibat peningkatan penjualan satu unit.
- Optimasi: Turunan digunakan untuk menentukan titik optimum dalam berbagai masalah ekonomi, seperti menentukan tingkat produksi yang memaksimalkan keuntungan atau menentukan tingkat konsumsi yang memaksimalkan utilitas.
Aplikasi Konsep Integral Tentu dalam Bidang Teknik
Konsep integral tentu, yang mengukur luas daerah di bawah kurva, memiliki aplikasi penting dalam bidang teknik. Integral tentu digunakan untuk menghitung berbagai besaran, seperti volume, luas permukaan, dan momen inersia.
- Perhitungan Volume: Integral tentu dapat digunakan untuk menghitung volume benda padat yang rumit, seperti tabung, kerucut, dan bola, dengan menggunakan metode penampang.
- Perhitungan Luas Permukaan: Integral tentu dapat digunakan untuk menghitung luas permukaan benda padat, seperti tabung, kerucut, dan bola, dengan menggunakan metode penampang.
- Perhitungan Momen Inersia: Integral tentu dapat digunakan untuk menghitung momen inersia benda padat, yang merupakan ukuran resistensi benda terhadap rotasi. Momen inersia penting dalam desain struktur dan mesin.
Aplikasi Konsep Limit Fungsi dalam Bidang Fisika, Soal dan jawaban matematika kelas 12
Konsep limit fungsi, yang mengukur nilai fungsi ketika variabel mendekati nilai tertentu, memiliki aplikasi penting dalam bidang fisika. Limit digunakan untuk menganalisis perilaku fungsi dalam situasi yang ekstrem, seperti kecepatan sesaat dan percepatan sesaat.
- Kecepatan Sesaat: Kecepatan sesaat suatu benda adalah laju perubahan posisi benda terhadap waktu pada suatu titik tertentu. Konsep limit digunakan untuk menghitung kecepatan sesaat dengan mengambil limit kecepatan rata-rata ketika selang waktu mendekati nol.
- Percepatan Sesaat: Percepatan sesaat suatu benda adalah laju perubahan kecepatan benda terhadap waktu pada suatu titik tertentu. Konsep limit digunakan untuk menghitung percepatan sesaat dengan mengambil limit percepatan rata-rata ketika selang waktu mendekati nol.
- Turunan: Konsep limit digunakan untuk mendefinisikan turunan suatu fungsi, yang merupakan laju perubahan fungsi terhadap variabelnya. Turunan memiliki aplikasi penting dalam fisika, seperti menghitung kecepatan, percepatan, dan gaya.
Penggunaan Vektor dalam Bidang Navigasi
Vektor, yang merupakan besaran yang memiliki besar dan arah, memiliki aplikasi penting dalam bidang navigasi. Vektor digunakan untuk merepresentasikan posisi, kecepatan, dan arah objek, serta untuk menghitung jarak dan waktu tempuh.
- Navigasi Udara: Vektor digunakan untuk menghitung kecepatan dan arah pesawat terbang, serta untuk menentukan posisi pesawat terbang relative terhadap tanah.
- Navigasi Laut: Vektor digunakan untuk menghitung kecepatan dan arah kapal laut, serta untuk menentukan posisi kapal laut relative terhadap tanah.
- Sistem GPS: Sistem GPS menggunakan vektor untuk menentukan posisi objek di bumi dengan menggunakan sinyal dari satelit.
Aplikasi Matriks dalam Bidang Statistika
Matriks, yang merupakan susunan bilangan dalam baris dan kolom, memiliki aplikasi penting dalam bidang statistika. Matriks digunakan untuk merepresentasikan data statistik, serta untuk melakukan berbagai operasi statistik, seperti analisis regresi, analisis faktor, dan analisis klaster.
- Analisis Regresi: Matriks digunakan untuk menghitung koefisien regresi dalam analisis regresi, yang mengukur hubungan antara variabel independen dan variabel dependen.
- Analisis Faktor: Matriks digunakan untuk mengidentifikasi faktor-faktor laten yang menjelaskan variasi dalam data statistik.
- Analisis Klaster: Matriks digunakan untuk mengelompokkan data statistik menjadi kelompok-kelompok yang memiliki kesamaan.
Latihan Soal dan Jawaban
Untuk menguji pemahaman dan mengasah kemampuan berpikir kritis dalam matematika kelas 12, berikut disajikan beberapa soal latihan beserta jawabannya. Soal-soal ini mencakup berbagai topik penting yang dipelajari di kelas 12, dan dirancang untuk membantu kamu dalam memahami konsep-konsep yang telah dipelajari.
Soal Latihan
Soal-soal latihan berikut ini dirancang untuk menguji pemahaman konsep dan kemampuan berpikir kritis dalam berbagai topik matematika kelas 12. Bacalah setiap soal dengan cermat dan kerjakan dengan langkah-langkah yang tepat.
- Turunan dan Aplikasi
Tentukan turunan pertama dari fungsi f(x) = x3 + 2x2 – 5x + 1.
- Integral dan Aplikasi
Hitunglah integral tak tentu dari fungsi f(x) = 2x + 3.
- Limit dan Kekontinuan
Tentukan nilai limit dari fungsi f(x) = (x2 – 4) / (x – 2) saat x mendekati 2.
- Persamaan dan Pertidaksamaan
Selesaikan persamaan kuadrat x2 – 5x + 6 = 0.
- Trigonometri
Tentukan nilai sin 30°.
Jawaban Soal Latihan
Berikut adalah jawaban untuk setiap soal latihan yang telah diberikan. Pastikan kamu memahami langkah-langkah yang digunakan untuk menyelesaikan setiap soal.
- Turunan dan Aplikasi
Turunan pertama dari fungsi f(x) = x3 + 2x2 – 5x + 1 adalah f'(x) = 3x2 + 4x – 5.
- Integral dan Aplikasi
Integral tak tentu dari fungsi f(x) = 2x + 3 adalah F(x) = x2 + 3x + C, dengan C adalah konstanta integrasi.
- Limit dan Kekontinuan
Nilai limit dari fungsi f(x) = (x2 – 4) / (x – 2) saat x mendekati 2 adalah 4. Hal ini dapat dihitung dengan menggunakan pemfaktoran dan penyederhanaan fungsi.
- Persamaan dan Pertidaksamaan
Persamaan kuadrat x2 – 5x + 6 = 0 dapat diselesaikan dengan menggunakan faktorisasi atau rumus kuadrat. Solusi dari persamaan ini adalah x = 2 dan x = 3.
- Trigonometri
Nilai sin 30° adalah 1/2. Ini adalah salah satu nilai trigonometri dasar yang perlu kamu ingat.
Terakhir
Dengan memahami konsep-konsep matematika kelas 12 dan melatih kemampuan memecahkan soal, kamu akan lebih siap menghadapi ujian dan menerapkan ilmu matematika dalam berbagai bidang kehidupan. Matematika bukan hanya sekadar rumus, tetapi juga alat untuk berpikir logis dan menyelesaikan masalah secara sistematis. Jadi, jangan takut untuk terus belajar dan berlatih agar kamu bisa menguasai matematika dengan baik!







