Contoh Soal Akar Sekawan: Menguak Rahasia Bilangan Irasional

Contoh soal akar sekawan – Akar sekawan, mungkin terdengar asing di telinga, namun sebenarnya konsep ini hadir dalam berbagai aspek kehidupan. Bayangkan sebuah segitiga siku-siku dengan sisi miring yang panjangnya 5 cm dan salah satu sisi tegaknya 2 cm. Bagaimana kita bisa menghitung panjang sisi tegak lainnya? Di sinilah akar sekawan berperan penting.

Akar sekawan adalah pasangan dari sebuah bentuk akar yang jika dikalikan menghasilkan bilangan rasional. Konsep ini membantu kita dalam menyederhanakan bentuk akar, memecahkan persamaan, dan bahkan dalam memahami rumus-rumus matematika yang lebih kompleks.

Pengertian Akar Sekawan

Dalam matematika, akar sekawan merupakan konsep penting yang berhubungan dengan operasi akar kuadrat. Akar sekawan dari suatu bilangan merupakan pasangan bilangan yang ketika dikalikan menghasilkan hasil yang rasional. Konsep ini memiliki aplikasi yang luas, khususnya dalam penyederhanaan bentuk akar dan penyelesaian persamaan kuadrat.

Pengertian Akar Sekawan

Akar sekawan dari suatu bilangan adalah pasangan bilangan yang ketika dikalikan menghasilkan hasil yang rasional. Dengan kata lain, akar sekawan merupakan pasangan bilangan yang memiliki bentuk yang sama tetapi tanda yang berbeda pada bagian akar kuadratnya.

Sebagai contoh, akar sekawan dari bilangan $a + \sqrtb$ adalah $a – \sqrtb$. Ketika kedua bilangan ini dikalikan, kita peroleh:

$(a + \sqrtb)(a – \sqrtb) = a^2 – (\sqrtb)^2 = a^2 – b$

Hasil perkalian tersebut adalah $a^2 – b$, yang merupakan bilangan rasional. Hal ini menunjukkan bahwa $a + \sqrtb$ dan $a – \sqrtb$ merupakan pasangan akar sekawan.

Perbedaan Akar Sekawan dan Akar Biasa

Berikut tabel yang membandingkan akar sekawan dengan akar biasa:

Karakteristik	Akar Sekawan	Akar Biasa
Definisi	Pasangan bilangan yang ketika dikalikan menghasilkan hasil rasional.	Bilangan yang dikalikan dengan dirinya sendiri menghasilkan bilangan asli.
Sifat	Memiliki bentuk yang sama tetapi tanda yang berbeda pada bagian akar kuadratnya.	Tidak memiliki pasangan khusus yang menghasilkan bilangan rasional ketika dikalikan.
Contoh	$a + \sqrtb$ dan $a – \sqrtb$	$\sqrt2$, $\sqrt3$, $\sqrt5$

Mencari Akar Sekawan

Dalam matematika, akar sekawan merupakan konsep penting dalam menyederhanakan bentuk akar. Akar sekawan dari suatu bilangan merupakan bilangan lain yang, ketika dikalikan dengan bilangan asli, menghasilkan hasil yang rasional (tanpa akar).

Mencari Akar Sekawan

Mencari akar sekawan dari suatu bilangan cukup mudah. Berikut langkah-langkahnya:

1. Identifikasi bentuk bilangan yang ingin dicari akar sekawannya. Pastikan bilangan tersebut dalam bentuk a + b√c, di mana a, b, dan c adalah bilangan bulat, dan c adalah bilangan prima.
2. Untuk menemukan akar sekawan, ubah tanda di depan akar kuadrat. Jika bilangan aslinya adalah a + b√c, maka akar sekawannya adalah a – b√c.

Contoh Pencarian Akar Sekawan

Misalnya, kita ingin mencari akar sekawan dari bilangan 5 + 2√3. Berikut langkah-langkahnya:

1. Bilangan 5 + 2√3 sudah dalam bentuk a + b√c, di mana a = 5, b = 2, dan c = 3.
2. Untuk menemukan akar sekawan, kita ubah tanda di depan akar kuadrat. Sehingga akar sekawan dari 5 + 2√3 adalah 5 – 2√3.

Soal Cerita Akar Sekawan

Soal cerita akar sekawan merupakan jenis soal yang menantang kemampuan kita dalam memahami konsep akar sekawan dan menerapkannya dalam konteks yang lebih luas. Soal ini biasanya melibatkan situasi nyata yang berhubungan dengan geometri, aljabar, atau bahkan masalah sehari-hari. Untuk menyelesaikan soal cerita akar sekawan, kita perlu memahami hubungan antara akar sekawan dan konsep-konsep matematika lainnya, seperti luas, keliling, dan persamaan kuadrat.

Contoh Soal Cerita Akar Sekawan

Berikut ini adalah contoh soal cerita yang melibatkan konsep akar sekawan:

Sebuah taman berbentuk persegi panjang memiliki panjang 2√3 meter lebih panjang dari lebarnya. Jika luas taman tersebut adalah 12√3 meter persegi, tentukan panjang dan lebar taman tersebut.

Langkah-langkah Penyelesaian Soal Cerita Akar Sekawan

Untuk menyelesaikan soal cerita akar sekawan, kita dapat mengikuti langkah-langkah berikut:

1. Menerjemahkan soal cerita ke dalam bentuk persamaan matematika.
2. Menentukan variabel yang akan digunakan.
3. Menuliskan persamaan yang sesuai dengan informasi yang diberikan.
4. Menyelesaikan persamaan tersebut dengan menggunakan konsep akar sekawan.
5. Menghitung nilai variabel yang dicari.
6. Menuliskan jawaban akhir dalam bentuk yang sesuai dengan konteks soal.

Langkah-langkah Penyelesaian Soal Cerita

Berikut ini adalah langkah-langkah penyelesaian soal cerita tentang taman persegi panjang di atas:

1. Misalkan lebar taman adalah x meter. Maka panjang taman adalah x + 2√3 meter.
2. Luas taman adalah hasil kali panjang dan lebar, sehingga:
   

   x(x + 2√3) = 12√3

3. Sederhanakan persamaan tersebut:
   

   x² + 2√3x – 12√3 = 0

4. Persamaan tersebut merupakan persamaan kuadrat. Kita dapat menyelesaikannya dengan menggunakan rumus abc:
   

   x = (-b ± √(b² – 4ac)) / 2a

   di mana a = 1, b = 2√3, dan c = -12√3.

5. Substitusikan nilai a, b, dan c ke dalam rumus abc:
   

   x = (-2√3 ± √((2√3)² – 4(1)(-12√3))) / 2(1)

   x = (-2√3 ± √(12 + 48√3)) / 2

   x = (-2√3 ± √(12(1 + 4√3))) / 2

   x = (-2√3 ± 2√3(1 + 4√3)) / 2

   x = -√3 ± √3(1 + 4√3)

6. Kita memperoleh dua kemungkinan nilai x:
   

   x₁ = -√3 + √3(1 + 4√3) = 4√3

   x₂ = -√3 – √3(1 + 4√3) = -6√3

7. Karena lebar taman tidak mungkin bernilai negatif, maka lebar taman adalah 4√3 meter. Panjang taman adalah 4√3 + 2√3 = 6√3 meter.

Kesulitan dalam Memahami Akar Sekawan

Konsep akar sekawan merupakan salah satu materi penting dalam matematika, khususnya dalam aljabar. Materi ini seringkali menjadi tantangan bagi siswa karena melibatkan pemahaman tentang bilangan kompleks dan manipulasi aljabar yang rumit. Namun, dengan pendekatan yang tepat, pemahaman terhadap akar sekawan dapat dicapai dengan mudah.

Identifikasi Kesulitan

Beberapa kesulitan yang sering dihadapi siswa dalam memahami konsep akar sekawan antara lain:

• Kesulitan dalam memahami definisi akar sekawan. Akar sekawan adalah pasangan bilangan kompleks yang memiliki bagian real yang sama tetapi bagian imajinernya berlawanan tanda. Siswa mungkin kesulitan dalam membedakan antara bilangan kompleks dan akar sekawannya.
• Kesulitan dalam menerapkan konsep akar sekawan dalam menyelesaikan persamaan kuadrat. Siswa mungkin tidak memahami bagaimana akar sekawan digunakan untuk mencari solusi persamaan kuadrat yang tidak memiliki akar real.
• Kesulitan dalam melakukan operasi aljabar dengan akar sekawan. Siswa mungkin kesulitan dalam mengalikan, membagi, dan menyederhanakan ekspresi yang melibatkan akar sekawan.

Saran untuk Mengatasi Kesulitan

Berikut beberapa saran untuk mengatasi kesulitan dalam memahami konsep akar sekawan:

• Gunakan contoh yang sederhana dan mudah dipahami. Misalnya, tunjukkan bagaimana akar sekawan digunakan untuk mencari solusi persamaan kuadrat sederhana seperti x² + 1 = 0.
• Gunakan visualisasi untuk membantu siswa memahami konsep akar sekawan. Misalnya, gunakan diagram untuk menunjukkan hubungan antara bilangan kompleks dan akar sekawannya.
• Berikan latihan yang cukup untuk membantu siswa menguasai konsep akar sekawan. Latihan dapat mencakup soal-soal yang melibatkan operasi aljabar dengan akar sekawan dan penerapan konsep akar sekawan dalam menyelesaikan persamaan kuadrat.

Contoh Soal Akar Sekawan

Berikut adalah contoh soal akar sekawan yang dapat membantu siswa dalam memahami konsep ini:

• Tentukan akar sekawan dari bilangan kompleks 2 + 3i.
• Selesaikan persamaan kuadrat x² + 4x + 5 = 0 dengan menggunakan konsep akar sekawan.
• Sederhanakan ekspresi (2 + i)(3 – 2i) dengan menggunakan konsep akar sekawan.

Pentingnya Memahami Akar Sekawan

Memahami konsep akar sekawan sangat penting dalam berbagai bidang matematika dan ilmu pengetahuan, seperti:

• Aljabar: Akar sekawan digunakan untuk menyelesaikan persamaan kuadrat, mencari solusi persamaan polinomial, dan menyederhanakan ekspresi aljabar.
• Geometri: Akar sekawan digunakan untuk menghitung panjang dan sudut dalam geometri kompleks.
• Fisika: Akar sekawan digunakan untuk menyelesaikan persamaan gerak, persamaan gelombang, dan persamaan elektromagnetik.
• Teknik: Akar sekawan digunakan untuk merancang sistem kontrol, menganalisis sinyal, dan menyelesaikan masalah dalam mekanika fluida.

Strategi Mengerjakan Soal Akar Sekawan: Contoh Soal Akar Sekawan

Akar sekawan adalah konsep matematika yang penting dalam aljabar. Memahami konsep ini dan strategi untuk menyelesaikan soal-soal yang berhubungan dengan akar sekawan akan sangat membantu dalam meningkatkan pemahaman dan kemampuanmu dalam menyelesaikan masalah matematika. Ada beberapa strategi efektif yang dapat kamu gunakan untuk menguasai materi ini, mulai dari memahami konsep dasar hingga latihan soal secara rutin.

Contoh soal akar sekawan sering muncul dalam pelajaran matematika. Konsepnya erat kaitannya dengan penyelesaian persamaan kuadrat. Nah, untuk memahami lebih lanjut tentang sistem persamaan linear dua variabel, kamu bisa cek contoh-contoh soalnya di sini. Kemampuan menyelesaikan sistem persamaan linear dua variabel berguna untuk memecahkan soal akar sekawan, karena keduanya saling berhubungan.

Memahami Konsep Dasar Akar Sekawan

Langkah pertama yang perlu kamu lakukan adalah memahami konsep dasar akar sekawan. Akar sekawan dari suatu bilangan adalah bilangan lain yang jika dikalikan dengan bilangan tersebut akan menghasilkan hasil berupa bilangan rasional. Contohnya, akar sekawan dari √2 adalah -√2, karena (√2)(-√2) = -2.

Memahami konsep ini akan membantu kamu dalam mengidentifikasi akar sekawan dari suatu bilangan dan menggunakannya dalam menyelesaikan soal. Selain itu, memahami konsep dasar ini juga akan membantu kamu dalam memahami sifat-sifat akar sekawan, seperti:

• Akar sekawan dari suatu bilangan adalah negatif dari bilangan tersebut.
• Hasil kali dari suatu bilangan dengan akar sekawannya selalu menghasilkan bilangan rasional.
• Akar sekawan dari suatu bilangan dapat digunakan untuk menyederhanakan bentuk aljabar yang melibatkan akar.

Latihan Soal

Setelah memahami konsep dasar, latihan soal secara rutin adalah kunci untuk menguasai materi akar sekawan. Semakin banyak soal yang kamu kerjakan, semakin terbiasa kamu dalam mengidentifikasi akar sekawan dan menerapkannya dalam berbagai situasi.

Kamu dapat memulai dengan soal-soal dasar dan kemudian secara bertahap meningkatkan tingkat kesulitannya. Selain itu, kamu juga dapat mencoba untuk menyelesaikan soal-soal yang telah dikerjakan sebelumnya dengan cara yang berbeda untuk meningkatkan kemampuanmu dalam memecahkan masalah.

Berikut adalah beberapa contoh soal akar sekawan yang dapat kamu coba:

1. Tentukan akar sekawan dari √3.
2. Sederhanakan bentuk aljabar √2 + √8.
3. Tentukan nilai x yang memenuhi persamaan √x + √4 = 5.

Menggunakan Rumus

Selain memahami konsep dasar dan latihan soal, kamu juga dapat menggunakan rumus untuk menyelesaikan soal-soal akar sekawan. Rumus yang paling umum digunakan adalah rumus kuadrat, yang dapat digunakan untuk menyelesaikan persamaan kuadrat yang melibatkan akar sekawan. Rumus ini dapat digunakan untuk mencari akar-akar persamaan kuadrat, yang kemudian dapat digunakan untuk menentukan akar sekawan dari suatu bilangan.

Rumus kuadrat:
x = (-b ± √(b² – 4ac)) / 2a

Dimana a, b, dan c adalah koefisien persamaan kuadrat ax² + bx + c = 0.

Contoh Penerapan Rumus

Misalkan kamu ingin mencari akar sekawan dari √3. Pertama, kamu perlu menentukan persamaan kuadrat yang akarnya adalah √3 dan akar sekawannya. Persamaan kuadrat ini dapat dibentuk dengan menggunakan sifat akar sekawan, yaitu hasil kali dari suatu bilangan dengan akar sekawannya selalu menghasilkan bilangan rasional.

Dalam kasus ini, hasil kali √3 dengan akar sekawannya adalah -3. Jadi, persamaan kuadrat yang akarnya adalah √3 dan akar sekawannya adalah x² – 3 = 0. Dengan menggunakan rumus kuadrat, kita dapat mencari akar-akar persamaan ini, yaitu x = √3 dan x = -√3. Jadi, akar sekawan dari √3 adalah -√3.

Strategi Lainnya

Selain strategi-strategi yang telah disebutkan di atas, kamu juga dapat menggunakan strategi lain untuk mengerjakan soal-soal akar sekawan, seperti:

• Mencari pola dalam soal-soal yang telah dikerjakan.
• Membuat diagram atau gambar untuk membantu dalam memahami soal.
• Meminta bantuan dari guru atau teman.

Tips dan Trik Akar Sekawan

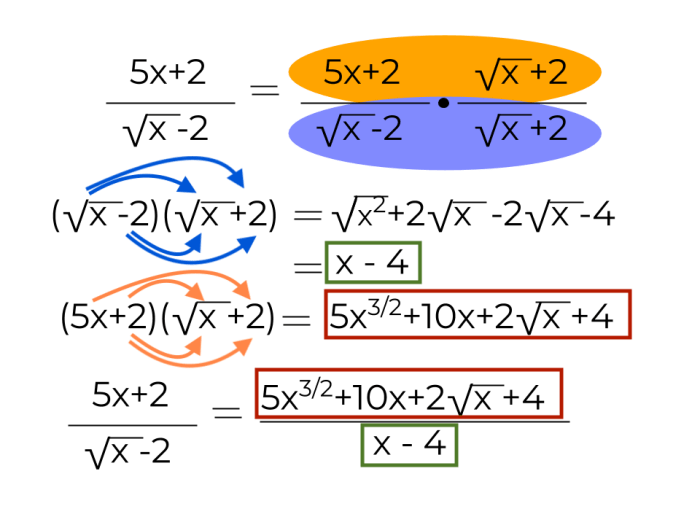
Akar sekawan adalah konsep matematika yang sering muncul dalam soal-soal, baik di tingkat sekolah menengah pertama maupun sekolah menengah atas. Konsep ini penting karena berkaitan dengan penyelesaian persamaan kuadrat dan operasi aljabar lainnya. Untuk memudahkan memahami dan menyelesaikan soal-soal akar sekawan, berikut ini beberapa tips dan trik yang bisa Anda terapkan.

Mengenal Sifat Akar Sekawan

Akar sekawan dari suatu bilangan adalah bilangan yang diperoleh dengan mengubah tanda operasi akar. Misalnya, akar sekawan dari √2 adalah -√2. Sifat penting dari akar sekawan adalah hasil perkaliannya selalu menghasilkan bilangan rasional.

• Contoh: (√2 + √3) x (√2 – √3) = (√2)² – (√3)² = 2 – 3 = -1

Menggunakan Rumus Akar Sekawan, Contoh soal akar sekawan

Rumus akar sekawan dapat digunakan untuk menyederhanakan bentuk pecahan yang mengandung akar. Rumus ini didasarkan pada sifat akar sekawan yang telah dijelaskan sebelumnya.

Rumus: 1 / (a + √b) = (a – √b) / (a² – b)

Contoh: Sederhanakan bentuk pecahan 1 / (2 + √3).

• Gunakan rumus akar sekawan: 1 / (2 + √3) = (2 – √3) / (2² – 3)
• Sederhanakan: (2 – √3) / (4 – 3) = 2 – √3

Menggunakan Kalkulator

Kalkulator dapat membantu Anda menghitung akar sekawan, terutama untuk bilangan yang kompleks. Namun, pastikan Anda memahami konsep akar sekawan sebelum menggunakan kalkulator.

• Contoh: Untuk menghitung akar sekawan dari √5, Anda dapat menggunakan tombol “√” pada kalkulator.

Menghindari Kesalahan Umum

Beberapa kesalahan umum yang sering terjadi dalam mengerjakan soal akar sekawan adalah:

• Salah mendefinisikan akar sekawan
• Salah menggunakan rumus akar sekawan
• Tidak menyederhanakan bentuk pecahan setelah menggunakan rumus akar sekawan

Simpulan Akhir

Memahami akar sekawan membuka pintu menuju pemahaman yang lebih dalam tentang dunia bilangan. Dengan latihan yang cukup, kita dapat menguasai konsep ini dan menggunakannya untuk menyelesaikan berbagai masalah matematika yang menarik.