Contoh soal kongruen dan kesebangunan – Pernahkah Anda memperhatikan bagaimana dua benda terlihat sama persis, seperti dua buah sepatu atau dua lembar kertas? Atau bagaimana sebuah peta kecil mampu mewakili wilayah yang luas? Di balik fenomena tersebut, terdapat konsep matematika yang menarik, yaitu kongruen dan kesebangunan. Kedua konsep ini membantu kita memahami hubungan antara bentuk dan ukuran, dan bagaimana mereka dapat saling berhubungan.
Dalam artikel ini, kita akan menjelajahi dunia kongruen dan kesebangunan melalui contoh soal yang menarik. Anda akan belajar tentang definisi, syarat, jenis-jenis transformasi geometri, dan aplikasi nyata dari kedua konsep ini. Siap untuk mengasah kemampuan berpikir kritis dan geometri Anda? Mari kita mulai!
Pengertian Kongruen dan Kesebangunan
Dalam dunia geometri, kita seringkali menjumpai bentuk-bentuk yang mirip atau bahkan identik. Untuk membedakannya, kita menggunakan konsep kongruen dan kesebangunan. Kedua konsep ini membantu kita memahami hubungan antara berbagai bentuk geometri dan bagaimana mereka saling berhubungan.
Definisi Kongruen dan Kesebangunan
Kongruen dan kesebangunan merupakan dua konsep penting dalam geometri yang membantu kita memahami hubungan antara berbagai bentuk geometri. Kedua konsep ini memiliki perbedaan yang signifikan meskipun keduanya membahas tentang kesamaan bentuk.
- Kongruen: Dua bangun geometri dikatakan kongruen jika mereka memiliki bentuk dan ukuran yang sama. Artinya, semua sisi dan sudut yang bersesuaian pada kedua bangun tersebut memiliki ukuran yang sama. Kita bisa menganggap bangun kongruen sebagai salinan yang identik dari bangun lainnya.
- Kesebangunan: Dua bangun geometri dikatakan sebangun jika mereka memiliki bentuk yang sama tetapi ukurannya berbeda. Artinya, semua sudut yang bersesuaian pada kedua bangun tersebut memiliki ukuran yang sama, sedangkan sisi-sisi yang bersesuaian memiliki perbandingan yang sama. Kita bisa menganggap bangun sebangun sebagai versi diperbesar atau diperkecil dari bangun lainnya.
Contoh Kongruen dan Kesebangunan dalam Kehidupan Sehari-hari
Konsep kongruen dan kesebangunan banyak ditemukan dalam kehidupan sehari-hari. Berikut beberapa contohnya:
- Kongruen:
- Dua lembar uang kertas dengan nominal yang sama.
- Dua buah sepatu yang sama ukurannya.
- Dua buah jendela pada sebuah rumah yang memiliki bentuk dan ukuran yang sama.
- Kesebangunan:
- Foto asli dan foto hasil cetak yang diperbesar atau diperkecil.
- Model miniatur sebuah gedung dan gedung aslinya.
- Bayangan sebuah pohon dan pohon aslinya pada saat matahari terik.
Perbedaan Ciri-ciri Kongruen dan Kesebangunan
Berikut tabel yang membandingkan ciri-ciri kongruen dan kesebangunan:
| Ciri | Kongruen | Kesebangunan |
|---|---|---|
| Bentuk | Sama | Sama |
| Ukuran | Sama | Berbeda |
| Sudut yang Bersesuaian | Sama | Sama |
| Sisi yang Bersesuaian | Sama | Berbanding Sama |
Syarat Kongruen dan Kesebangunan
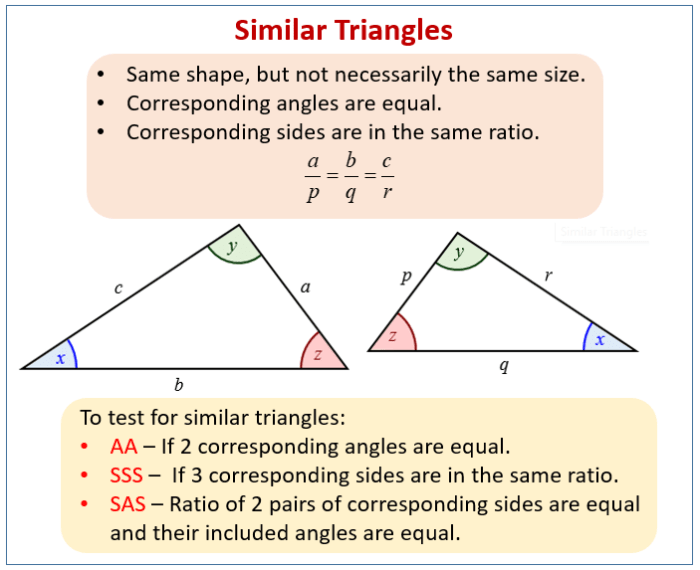
Dalam geometri, dua bangun datar dikatakan kongruen jika mereka memiliki bentuk dan ukuran yang sama. Sementara itu, dua bangun datar dikatakan sebangun jika mereka memiliki bentuk yang sama tetapi ukurannya berbeda.
Syarat Kongruen
Dua bangun datar dikatakan kongruen jika memenuhi syarat berikut:
- Sisi-Sisi-Sisi (SSS): Jika ketiga sisi dari satu bangun datar sama panjang dengan ketiga sisi dari bangun datar lainnya, maka kedua bangun datar tersebut kongruen.
- Sisi-Sudut-Sisi (SAS): Jika dua sisi dan sudut apitnya dari satu bangun datar sama dengan dua sisi dan sudut apitnya dari bangun datar lainnya, maka kedua bangun datar tersebut kongruen.
- Sudut-Sisi-Sudut (ASA): Jika dua sudut dan sisi di antara keduanya dari satu bangun datar sama dengan dua sudut dan sisi di antara keduanya dari bangun datar lainnya, maka kedua bangun datar tersebut kongruen.
- Sudut-Sudut-Sisi (SSA): Jika dua sudut dan sisi yang berhadapan dengan salah satu sudut dari satu bangun datar sama dengan dua sudut dan sisi yang berhadapan dengan salah satu sudut dari bangun datar lainnya, maka kedua bangun datar tersebut kongruen.
Syarat Kesebangunan
Dua bangun datar dikatakan sebangun jika memenuhi syarat berikut:
- Sisi-Sisi-Sisi (SSS): Jika perbandingan ketiga sisi dari satu bangun datar sama dengan perbandingan ketiga sisi dari bangun datar lainnya, maka kedua bangun datar tersebut sebangun.
- Sisi-Sudut-Sisi (SAS): Jika dua sisi dan sudut apitnya dari satu bangun datar sebanding dengan dua sisi dan sudut apitnya dari bangun datar lainnya, maka kedua bangun datar tersebut sebangun.
- Sudut-Sudut-Sudut (AAA): Jika ketiga sudut dari satu bangun datar sama dengan ketiga sudut dari bangun datar lainnya, maka kedua bangun datar tersebut sebangun.
Perbedaan Syarat Kongruen dan Kesebangunan
Perbedaan utama antara syarat kongruen dan kesebangunan terletak pada ukuran bangun datar. Bangun datar yang kongruen memiliki ukuran yang sama, sedangkan bangun datar yang sebangun memiliki bentuk yang sama tetapi ukurannya berbeda. Misalnya, dua persegi panjang dengan panjang dan lebar yang sama adalah kongruen, sedangkan dua persegi panjang dengan panjang dan lebar yang berbeda adalah sebangun.
Contoh Soal Kongruen
Kongruen merupakan konsep penting dalam geometri yang membahas tentang kesamaan bentuk dan ukuran dua bangun datar. Dua bangun datar dikatakan kongruen jika mereka memiliki bentuk dan ukuran yang sama persis, meskipun posisi atau orientasinya berbeda.
Contoh Soal Cerita tentang Dua Bangun Datar yang Kongruen
Sebuah toko kue ingin membuat dua jenis kue dengan bentuk yang sama, yaitu berbentuk persegi panjang. Kue pertama memiliki panjang 10 cm dan lebar 5 cm, sedangkan kue kedua memiliki panjang 10 cm dan lebar 5 cm. Kedua kue tersebut memiliki bentuk dan ukuran yang sama, meskipun posisi atau orientasinya berbeda.
Langkah-langkah Menentukan Dua Bangun Datar Kongruen
Untuk menentukan apakah dua bangun datar kongruen, kita dapat menggunakan beberapa metode, seperti:
- Membandingkan Panjang Sisi: Jika semua sisi dari kedua bangun datar memiliki panjang yang sama, maka kedua bangun datar tersebut kongruen.
- Membandingkan Besar Sudut: Jika semua sudut dari kedua bangun datar memiliki besar yang sama, maka kedua bangun datar tersebut kongruen.
- Mencari Kecocokan Sisi dan Sudut: Jika kita dapat menemukan kecocokan sisi dan sudut yang sama pada kedua bangun datar, maka kedua bangun datar tersebut kongruen.
Menentukan Panjang Sisi dan Besar Sudut pada Bangun Datar Kongruen
Jika dua bangun datar kongruen, maka panjang sisi dan besar sudut yang bersesuaian pada kedua bangun datar tersebut akan sama.
- Panjang Sisi: Panjang sisi yang bersesuaian pada kedua bangun datar kongruen akan memiliki nilai yang sama.
- Besar Sudut: Besar sudut yang bersesuaian pada kedua bangun datar kongruen akan memiliki nilai yang sama.
Contoh Soal Kesebangunan
Kesebangunan adalah konsep penting dalam geometri yang menjelaskan hubungan antara dua bangun datar yang memiliki bentuk yang sama tetapi ukuran yang berbeda. Dua bangun datar dikatakan sebangun jika sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian sebanding. Konsep ini memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti dalam pembuatan peta, desain arsitektur, dan bahkan dalam fotografi.
Contoh Soal Cerita Kesebangunan
Bayangkan sebuah taman bermain yang memiliki dua buah ayunan, ayunan A dan ayunan B. Ayunan A memiliki panjang tali 2 meter, sedangkan ayunan B memiliki panjang tali 3 meter. Kedua ayunan memiliki bentuk yang sama, yaitu segitiga sama kaki, tetapi ukurannya berbeda.
Bagaimana cara menentukan apakah kedua ayunan tersebut sebangun? Dan bagaimana cara menentukan perbandingan sisi dan besar sudut pada kedua ayunan tersebut?
Langkah-langkah Menentukan Kesebangunan
- Identifikasi sudut-sudut yang bersesuaian: Pada kedua ayunan, sudut puncak segitiga sama kaki adalah sudut yang sama besar. Begitu juga dengan sudut-sudut di dasar segitiga.
- Periksa perbandingan sisi-sisi yang bersesuaian: Pada ayunan A, panjang sisi alas adalah 2 meter dan panjang sisi miring adalah 2 meter. Pada ayunan B, panjang sisi alas adalah 3 meter dan panjang sisi miring adalah 3 meter. Perbandingan sisi-sisi yang bersesuaian adalah 2/3 = 2/3.
- Kesimpulan: Karena sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian sebanding, maka kedua ayunan tersebut sebangun.
Menentukan Perbandingan Sisi dan Sudut, Contoh soal kongruen dan kesebangunan
Perbandingan sisi-sisi yang bersesuaian pada dua bangun datar yang sebangun adalah sama. Dalam contoh ayunan, perbandingan sisi-sisi adalah 2/3. Artinya, setiap sisi pada ayunan B adalah 3/2 kali lebih panjang daripada sisi yang bersesuaian pada ayunan A.
Sudut-sudut yang bersesuaian pada dua bangun datar yang sebangun memiliki ukuran yang sama. Dalam contoh ayunan, sudut puncak pada kedua ayunan sama besar, begitu juga dengan sudut-sudut di dasar segitiga.
Penerapan Kongruen dan Kesebangunan dalam Kehidupan Sehari-hari: Contoh Soal Kongruen Dan Kesebangunan
Konsep kongruen dan kesebangunan, yang mempelajari kesamaan bentuk dan ukuran, ternyata punya aplikasi luas dalam kehidupan sehari-hari. Dari arsitektur hingga pembuatan peta, konsep ini berperan penting dalam memastikan ketepatan, efisiensi, dan keindahan.
Arsitektur, Desain, dan Teknik
Dalam dunia arsitektur, desain, dan teknik, konsep kongruen dan kesebangunan berperan penting dalam menciptakan struktur yang aman dan estetis. Misalnya, ketika merancang rumah, arsitek menggunakan konsep kesebangunan untuk memastikan proporsi ruangan dan fasad bangunan sesuai.
Contoh soal kongruen dan kesebangunan seringkali melibatkan perbandingan sisi dan sudut. Nah, kalau kamu ingin memprediksi apa yang akan terjadi di masa depan, kamu bisa menggunakan tenses yang tepat, seperti future tense. Misalnya, “Saya akan belajar tentang contoh soal future tense di sini.” Nah, kembali ke contoh soal kongruen dan kesebangunan, perhatikan dengan baik apakah bentuk dan ukuran dua bangun sama atau hanya proporsional.
- Bangunan dengan Bentuk Simetris: Konsep kongruen digunakan untuk memastikan bahwa setiap sisi bangunan memiliki bentuk dan ukuran yang sama, sehingga menciptakan tampilan yang seimbang dan estetis.
- Desain Jembatan: Konsep kesebangunan digunakan dalam merancang jembatan untuk memastikan bahwa struktur tersebut dapat menopang beban dengan merata dan aman.
- Pembuatan Model: Model bangunan yang dibuat untuk presentasi atau simulasi menggunakan konsep kesebangunan untuk memastikan bahwa model tersebut memiliki proporsi yang sama dengan bangunan aslinya.
Pembuatan Peta dan Denah
Pembuatan peta dan denah juga mengandalkan konsep kesebangunan. Peta merupakan representasi grafis dari suatu wilayah, dan kesebangunan memastikan bahwa jarak dan bentuk pada peta proporsional dengan yang sebenarnya.
- Skala Peta: Skala peta menunjukkan perbandingan jarak pada peta dengan jarak sebenarnya di lapangan. Konsep kesebangunan memastikan bahwa semua bagian peta memiliki skala yang sama, sehingga jarak dan bentuk tetap proporsional.
- Denah Rumah: Denah rumah menunjukkan tata letak ruangan dan ukurannya. Konsep kesebangunan digunakan untuk memastikan bahwa denah rumah sesuai dengan ukuran sebenarnya, sehingga memudahkan perencanaan dan konstruksi.
Perhitungan Jarak dan Tinggi Objek
Konsep kongruen dan kesebangunan juga berguna dalam menghitung jarak dan tinggi objek. Dengan memanfaatkan kesamaan bentuk dan ukuran, kita dapat menentukan jarak atau tinggi objek yang sulit dijangkau.
- Mengukur Tinggi Pohon: Dengan menggunakan tongkat dan bayangan, kita dapat menghitung tinggi pohon dengan menerapkan konsep kesebangunan.
- Menentukan Jarak: Jika kita mengetahui jarak suatu objek dan ukurannya, kita dapat menentukan jarak objek lain yang sejenis dengan memanfaatkan konsep kesebangunan.
Soal Latihan Kongruen dan Kesebangunan
Setelah mempelajari konsep kongruen dan kesebangunan, mari kita uji pemahamanmu dengan beberapa soal latihan. Soal-soal ini akan membantumu mengasah kemampuan dalam mengidentifikasi dan menganalisis bentuk-bentuk geometri yang kongruen dan sebangun.
Soal Latihan
Berikut adalah 5 soal latihan tentang kongruen dan kesebangunan, lengkap dengan kunci jawabannya.
| No. | Soal | Kunci Jawaban |
|---|---|---|
| 1 | Dua segitiga dikatakan kongruen jika … | Dua segitiga dikatakan kongruen jika semua sisi dan sudutnya bersesuaian. |
| 2 | Dua persegi panjang dikatakan sebangun jika … | Dua persegi panjang dikatakan sebangun jika perbandingan sisi-sisi yang bersesuaian sama. |
| 3 | Perhatikan gambar dua segitiga berikut: [Gambar dua segitiga] Apakah kedua segitiga tersebut kongruen? Jelaskan alasanmu. |
Ya, kedua segitiga tersebut kongruen. Alasannya adalah karena kedua segitiga memiliki sisi-sisi yang bersesuaian sama panjang dan sudut-sudut yang bersesuaian sama besar. |
| 4 | Perhatikan gambar dua persegi panjang berikut: [Gambar dua persegi panjang] Apakah kedua persegi panjang tersebut sebangun? Jelaskan alasanmu. |
Ya, kedua persegi panjang tersebut sebangun. Alasannya adalah karena perbandingan sisi-sisi yang bersesuaian sama, yaitu 2:1. |
| 5 | Sebuah segitiga memiliki sisi-sisi dengan panjang 3 cm, 4 cm, dan 5 cm. Segitiga lainnya memiliki sisi-sisi dengan panjang 6 cm, 8 cm, dan 10 cm. Apakah kedua segitiga tersebut sebangun? Jelaskan alasanmu. | Ya, kedua segitiga tersebut sebangun. Alasannya adalah karena perbandingan sisi-sisi yang bersesuaian sama, yaitu 2:1. |
Ringkasan Akhir
Memahami konsep kongruen dan kesebangunan bukan hanya tentang belajar rumus dan teorema, tetapi juga tentang melihat dunia dengan perspektif baru. Dari arsitektur hingga desain, dari peta hingga teknik, konsep ini berperan penting dalam berbagai bidang. Semoga artikel ini telah membuka mata Anda terhadap keajaiban matematika yang tersembunyi di sekitar kita.






