Contoh soal perkalian polinomial beserta jawabannya – Pernahkah Anda bertanya-tanya bagaimana mengalikan dua atau lebih suku aljabar yang saling terkait? Nah, di situlah perkalian polinomial berperan! Perkalian polinomial adalah operasi dasar dalam aljabar yang membantu kita memahami dan menyelesaikan berbagai masalah matematika, terutama dalam bidang kalkulus dan geometri.

Artikel ini akan membahas secara detail tentang perkalian polinomial, mulai dari pengertian dasar hingga contoh soal beserta jawabannya. Kita akan mempelajari berbagai metode untuk menyelesaikan perkalian polinomial, termasuk metode FOIL, distributif, dan Horner. Dengan pemahaman yang kuat tentang perkalian polinomial, Anda akan siap untuk menghadapi berbagai tantangan dalam matematika dan ilmu pengetahuan.

Table of Contents:

Pengertian Perkalian Polinomial

Perkalian polinomial adalah proses penggabungan dua atau lebih polinomial dengan menggunakan operasi perkalian. Polinomial sendiri merupakan ekspresi aljabar yang terdiri dari variabel dan konstanta, yang dihubungkan dengan operasi penjumlahan, pengurangan, dan perkalian. Perkalian polinomial merupakan konsep dasar dalam aljabar yang sering kita jumpai dalam berbagai bidang, seperti matematika, fisika, dan teknik.

Contoh Perkalian Polinomial dalam Kehidupan Sehari-hari

Perkalian polinomial dapat ditemukan dalam berbagai situasi sehari-hari. Misalnya, ketika kita menghitung luas suatu ruangan, kita sebenarnya menggunakan perkalian polinomial. Jika panjang ruangan diwakili oleh variabel *p* dan lebarnya diwakili oleh variabel *l*, maka luas ruangan dapat dihitung dengan rumus *p* *l*. Rumus ini merupakan perkalian dari dua polinomial, yaitu *p* dan *l*.

Jenis-Jenis Perkalian Polinomial

Berikut adalah tabel yang merangkum jenis-jenis perkalian polinomial dan contohnya:

Jenis Perkalian	Contoh
Perkalian Monomial dengan Monomial	(2x) * (3x) = 6x²
Perkalian Monomial dengan Binomial	(2x) * (x + 1) = 2x² + 2x
Perkalian Binomial dengan Binomial	(x + 2) * (x + 3) = x² + 5x + 6
Perkalian Trinomial dengan Binomial	(x² + 2x + 1) * (x + 1) = x³ + 3x² + 3x + 1

Contoh Soal Perkalian Polinomial

Berikut adalah beberapa contoh soal perkalian polinomial beserta jawabannya:

1. Sederhanakanlah perkalian berikut: (2x + 3) * (x – 1)

Jawaban:
(2x + 3) * (x – 1) = 2x² – 2x + 3x – 3
= 2x² + x – 3

2. Tentukan hasil perkalian berikut: (x² + 2x – 1) * (x + 2)

Jawaban:
(x² + 2x – 1) * (x + 2) = x³ + 2x² + 2x² + 4x – x – 2
= x³ + 4x² + 3x – 2

3. Hitunglah hasil perkalian berikut: (3x – 2) * (2x + 1)

Jawaban:
(3x – 2) * (2x + 1) = 6x² + 3x – 4x – 2
= 6x² – x – 2

Metode Perkalian Polinomial

Ada beberapa metode yang dapat digunakan untuk melakukan perkalian polinomial, antara lain:

– Metode Distributif: Metode ini melibatkan distribusi setiap suku dari polinomial pertama ke setiap suku dari polinomial kedua.
– Metode FOIL: Metode ini hanya berlaku untuk perkalian binomial dengan binomial. FOIL merupakan singkatan dari First, Outer, Inner, Last. Metode ini melibatkan perkalian suku pertama dari kedua binomial, kemudian suku luar, kemudian suku dalam, dan terakhir suku terakhir dari kedua binomial.
– Metode Box: Metode ini melibatkan pembuatan tabel dengan baris dan kolom yang mewakili suku-suku dari kedua polinomial. Setiap sel dalam tabel berisi hasil perkalian dari suku baris dan kolom yang bersesuaian.

Pentingnya Memahami Perkalian Polinomial

Memahami konsep perkalian polinomial sangat penting dalam berbagai bidang, seperti:

– Matematika: Perkalian polinomial merupakan konsep dasar dalam aljabar yang digunakan untuk menyelesaikan persamaan, menyelesaikan sistem persamaan, dan mempelajari fungsi polinomial.
– Fisika: Perkalian polinomial digunakan dalam berbagai rumus fisika, seperti rumus kecepatan, percepatan, dan gaya.
– Teknik: Perkalian polinomial digunakan dalam berbagai aplikasi teknik, seperti perancangan jembatan, gedung, dan pesawat terbang.

Kesimpulan

Perkalian polinomial adalah konsep dasar dalam aljabar yang memiliki aplikasi yang luas dalam berbagai bidang. Memahami konsep ini akan sangat membantu dalam mempelajari matematika, fisika, dan teknik.

Prosedur Perkalian Polinomial

Perkalian polinomial merupakan operasi matematika yang melibatkan penggabungan suku-suku dalam dua atau lebih polinomial. Prosedur ini melibatkan pengalikan setiap suku dalam satu polinomial dengan setiap suku dalam polinomial lainnya, kemudian menjumlahkan hasil perkalian tersebut.

Langkah-langkah Perkalian Polinomial, Contoh soal perkalian polinomial beserta jawabannya

Untuk memahami langkah-langkah perkalian polinomial secara sistematis, perhatikan penjelasan berikut:

Identifikasi Suku-suku: Mulailah dengan mengidentifikasi semua suku dalam setiap polinomial. Ingat bahwa suku dalam polinomial dapat berupa konstanta, variabel, atau kombinasi keduanya.
Kalikan Setiap Suku: Kalikan setiap suku dalam polinomial pertama dengan setiap suku dalam polinomial kedua. Ingat untuk mengalikan koefisien dan variabelnya secara terpisah.
Gabungkan Suku Sejenis: Setelah melakukan perkalian, gabungkan suku-suku yang memiliki variabel dan pangkat yang sama. Misalnya, suku-suku dengan variabel x^2 digabungkan menjadi satu suku.
Sederhanakan Ekspresi: Setelah menggabungkan suku sejenis, sederhanakan ekspresi dengan menjumlahkan atau mengurangi koefisiennya.

Contoh Perkalian Polinomial dengan Dua Variabel

Misalnya, kita ingin mengalikan polinomial (2x + 3y) dengan (x – 2y). Berikut langkah-langkahnya:

Identifikasi Suku: Polinomial pertama memiliki suku 2x dan 3y, sedangkan polinomial kedua memiliki suku x dan -2y.
Kalikan Setiap Suku:
* 2x * x = 2x^2
* 2x * -2y = -4xy
* 3y * x = 3xy
* 3y * -2y = -6y^2
Gabungkan Suku Sejenis:
* 2x^2
* -4xy + 3xy = -xy
* -6y^2
Sederhanakan Ekspresi: Hasil perkalian dari (2x + 3y) dan (x – 2y) adalah 2x^2 – xy – 6y^2.

Metode Distributif dalam Perkalian Polinomial

Metode distributif merupakan cara yang efektif untuk mengalikan polinomial. Prinsipnya adalah mengalikan setiap suku dalam satu polinomial dengan setiap suku dalam polinomial lainnya.

Contohnya, jika kita ingin mengalikan (a + b) dengan (c + d), maka kita dapat menggunakan metode distributif seperti berikut:

(a + b) * (c + d) = a * (c + d) + b * (c + d)

Kemudian, kita distribusikan lagi:

a * (c + d) + b * (c + d) = ac + ad + bc + bd

Dengan menggunakan metode distributif, kita dapat mengalikan polinomial dengan lebih sistematis dan menghindari kesalahan dalam perkalian.

Contoh Soal Perkalian Polinomial

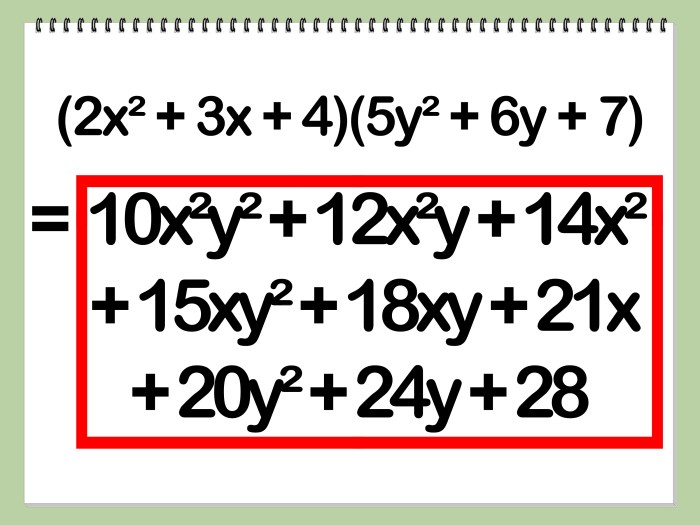
Perkalian polinomial merupakan operasi aljabar yang melibatkan penggandaan dua atau lebih polinomial. Operasi ini melibatkan perkalian setiap suku dari polinomial pertama dengan setiap suku dari polinomial kedua. Hasilnya adalah polinomial baru yang memiliki derajat yang lebih tinggi dari polinomial asli.

Contoh Soal Perkalian Polinomial

Berikut adalah beberapa contoh soal perkalian polinomial dengan tingkat kesulitan yang berbeda:

Soal 1:

(x + 2) (x + 3)

Jawaban:

x² + 5x + 6
Soal 2:

(2x – 1) (x + 4)

Jawaban:

2x² + 7x – 4
Soal 3:

(x² + 3x – 2) (x – 1)

Jawaban:

Contoh soal perkalian polinomial beserta jawabannya memang penting untuk dipelajari. Nah, buat kamu yang ingin memahami lebih dalam tentang perkalian polinomial, coba deh cek contoh soal pecahan biasa di sini. Memahami konsep pecahan biasa bisa membantumu dalam menyelesaikan soal perkalian polinomial, karena konsep dasar matematika saling berkaitan.

x³ + 2x² – 5x + 2
Soal 4:

(2x² + 5x – 3) (3x + 2)

Jawaban:

6x³ + 19x² + x – 6
Soal 5:

(x³ – 2x² + 4x – 1) (x² + x + 1)

Jawaban:

x⁵ – x⁴ + 6x³ – 3x² + 3x – 1

Tabel Contoh Soal dan Jawaban

Soal	Jawaban
(x + 2) (x + 3)	x² + 5x + 6
(2x – 1) (x + 4)	2x² + 7x – 4
(x² + 3x – 2) (x – 1)	x³ + 2x² – 5x + 2
(2x² + 5x – 3) (3x + 2)	6x³ + 19x² + x – 6
(x³ – 2x² + 4x – 1) (x² + x + 1)	x⁵ – x⁴ + 6x³ – 3x² + 3x – 1

Penerapan Perkalian Polinomial: Contoh Soal Perkalian Polinomial Beserta Jawabannya

Perkalian polinomial, selain menjadi konsep matematika yang penting, juga memiliki aplikasi yang luas dalam berbagai bidang. Kemampuan untuk mengalikan polinomial memungkinkan kita untuk menyelesaikan masalah kompleks dalam bidang seperti ilmu komputer, fisika, dan teknik.

Aplikasi Perkalian Polinomial

Perkalian polinomial memiliki berbagai aplikasi dalam berbagai bidang, termasuk:

Ilmu Komputer: Dalam ilmu komputer, perkalian polinomial digunakan dalam algoritma pemrosesan sinyal digital, seperti filter digital dan transformasi Fourier cepat (FFT). Perkalian polinomial juga digunakan dalam kriptografi untuk mengenkripsi dan mendekripsi data.
Fisika: Dalam fisika, perkalian polinomial digunakan untuk menyelesaikan persamaan gerak, persamaan gelombang, dan persamaan diferensial lainnya. Misalnya, dalam mekanika kuantum, polinomial digunakan untuk menggambarkan fungsi gelombang partikel.
Teknik: Perkalian polinomial digunakan dalam berbagai bidang teknik, seperti teknik elektro, teknik sipil, dan teknik kimia. Misalnya, dalam teknik elektro, polinomial digunakan untuk mendesain filter dan amplifier.
Ekonomi: Perkalian polinomial digunakan dalam ekonomi untuk memodelkan pertumbuhan ekonomi, inflasi, dan investasi.
Statistika: Perkalian polinomial digunakan dalam statistika untuk memodelkan hubungan antara variabel dan untuk mengestimasi parameter model.

Contoh Kasus Nyata: Desain Filter Digital

Salah satu contoh kasus nyata penggunaan perkalian polinomial adalah dalam desain filter digital. Filter digital digunakan untuk memisahkan sinyal yang diinginkan dari sinyal yang tidak diinginkan dalam sistem pemrosesan sinyal.

Dalam desain filter digital, perkalian polinomial digunakan untuk menentukan karakteristik filter, seperti frekuensi potong dan respon frekuensi. Filter digital sering kali direpresentasikan sebagai persamaan diferensial linier, yang dapat diselesaikan menggunakan perkalian polinomial.

Misalnya, filter digital sederhana dapat didefinisikan oleh persamaan berikut:

y(n) = a0*x(n) + a1*x(n-1) + a2*x(n-2)

Dimana:

* y(n) adalah sinyal output pada waktu n
* x(n) adalah sinyal input pada waktu n
* a0, a1, dan a2 adalah koefisien filter

Koefisien filter ini ditentukan melalui perkalian polinomial. Dengan mengalikan polinomial yang mewakili sinyal input dan filter, kita dapat memperoleh sinyal output. Proses ini memungkinkan kita untuk mendesain filter yang dapat memisahkan sinyal yang diinginkan dari sinyal yang tidak diinginkan.

Peran Perkalian Polinomial dalam Menyelesaikan Masalah

Perkalian polinomial berperan penting dalam menyelesaikan masalah dalam berbagai bidang karena:

* Representasi Fungsi Kompleks: Polinomial dapat digunakan untuk merepresentasikan fungsi kompleks yang muncul dalam berbagai masalah ilmiah dan teknik.
* Manipulasi Aljabar: Perkalian polinomial memungkinkan kita untuk memanipulasi fungsi kompleks secara aljabar, yang memungkinkan kita untuk menyelesaikan persamaan dan menemukan solusi untuk masalah.
* Analisis Data: Perkalian polinomial digunakan dalam analisis data untuk memodelkan hubungan antara variabel dan untuk mengestimasi parameter model.
* Pemrosesan Sinyal: Perkalian polinomial digunakan dalam pemrosesan sinyal untuk memanipulasi sinyal digital, seperti filter digital dan transformasi Fourier cepat (FFT).

Perkalian polinomial adalah alat yang kuat yang memiliki aplikasi yang luas dalam berbagai bidang. Kemampuan untuk mengalikan polinomial memungkinkan kita untuk menyelesaikan masalah kompleks yang muncul dalam berbagai disiplin ilmu.

Perkalian Polinomial dengan Metode FOIL

Metode FOIL adalah teknik yang digunakan untuk mengalikan dua binomial. Binomial adalah ekspresi aljabar yang terdiri dari dua suku. Metode ini memberikan cara sistematis untuk memastikan bahwa setiap suku dalam satu binomial dikalikan dengan setiap suku dalam binomial lainnya.

Penjelasan Metode FOIL

Metode FOIL adalah singkatan dari First, Outer, Inner, dan Last. Metode ini menguraikan langkah-langkah untuk mengalikan dua binomial:

First: Kalikan suku pertama dari setiap binomial.
Outer: Kalikan suku pertama dari binomial pertama dengan suku kedua dari binomial kedua.
Inner: Kalikan suku kedua dari binomial pertama dengan suku pertama dari binomial kedua.
Last: Kalikan suku kedua dari setiap binomial.

Langkah-langkah Metode FOIL

Berikut adalah langkah-langkah yang dapat diikuti untuk mengalikan dua binomial menggunakan metode FOIL:

Tulis kedua binomial yang akan dikalikan.
Kalikan suku pertama dari setiap binomial (First).
Kalikan suku pertama dari binomial pertama dengan suku kedua dari binomial kedua (Outer).
Kalikan suku kedua dari binomial pertama dengan suku pertama dari binomial kedua (Inner).
Kalikan suku kedua dari setiap binomial (Last).
Gabungkan semua suku yang dihasilkan dan sederhanakan hasilnya.

Contoh Soal Perkalian Polinomial dengan Metode FOIL

Misalnya, kita ingin mengalikan dua binomial berikut:

(x + 2) (x + 3)

Tulis kedua binomial yang akan dikalikan: (x + 2) (x + 3)
Kalikan suku pertama dari setiap binomial (First): x * x = x²
Kalikan suku pertama dari binomial pertama dengan suku kedua dari binomial kedua (Outer): x * 3 = 3x
Kalikan suku kedua dari binomial pertama dengan suku pertama dari binomial kedua (Inner): 2 * x = 2x
Kalikan suku kedua dari setiap binomial (Last): 2 * 3 = 6
Gabungkan semua suku yang dihasilkan dan sederhanakan hasilnya: x² + 3x + 2x + 6 = x² + 5x + 6

Jadi, hasil perkalian (x + 2) (x + 3) adalah x² + 5x + 6.

Perkalian Polinomial dengan Metode Distributif

Perkalian polinomial merupakan salah satu operasi dasar dalam aljabar. Metode distributif adalah salah satu cara yang umum digunakan untuk mengalikan polinomial.

Metode Distributif dalam Perkalian Polinomial

Metode distributif dalam perkalian polinomial melibatkan mengalikan setiap suku dalam satu polinomial dengan setiap suku dalam polinomial lainnya.

Langkah-langkah Metode Distributif dalam Perkalian Polinomial

Berikut langkah-langkah metode distributif dalam perkalian polinomial:

Tentukan setiap suku dalam kedua polinomial.
Kalikan setiap suku dalam polinomial pertama dengan setiap suku dalam polinomial kedua.
Gabungkan suku-suku sejenis yang dihasilkan.

Contoh Soal Perkalian Polinomial dengan Metode Distributif

Misalnya, kita ingin mengalikan polinomial (2x + 3) dengan (x – 1).

Tentukan suku-suku dalam kedua polinomial:
- Polinomial pertama: (2x + 3) memiliki suku 2x dan 3.
- Polinomial kedua: (x – 1) memiliki suku x dan -1.
Kalikan setiap suku dalam polinomial pertama dengan setiap suku dalam polinomial kedua:
- 2x * x = 2x²
- 2x * -1 = -2x
- 3 * x = 3x
- 3 * -1 = -3
Gabungkan suku-suku sejenis:
- 2x² – 2x + 3x – 3 = 2x² + x – 3

Jadi, hasil perkalian (2x + 3) dengan (x – 1) adalah 2x² + x – 3.

Perkalian Polinomial dengan Metode Horner

Metode Horner adalah teknik yang efisien untuk menghitung nilai suatu polinomial pada suatu titik tertentu. Metode ini juga dapat digunakan untuk mengalikan dua polinomial. Metode Horner memanfaatkan konsep substitusi dan operasi aritmetika dasar, sehingga memudahkan perhitungan, terutama untuk polinomial dengan derajat tinggi.

Penjelasan Metode Horner dalam Perkalian Polinomial

Metode Horner dapat digunakan untuk mengalikan dua polinomial dengan memanfaatkan sifat distributif perkalian. Dalam metode ini, kita akan mengubah bentuk polinomial menjadi bentuk yang lebih sederhana, sehingga memudahkan perhitungan.

Langkah-langkah Metode Horner dalam Perkalian Polinomial

Berikut adalah langkah-langkah yang dapat digunakan untuk mengalikan dua polinomial dengan metode Horner:

Tuliskan kedua polinomial yang akan dikalikan dalam bentuk baris horizontal, dengan koefisien dari setiap suku polinomial disusun berdasarkan pangkatnya. Pastikan untuk menambahkan tempat kosong untuk suku-suku yang tidak ada di polinomial.
Buat tabel dengan kolom sebanyak jumlah suku dalam polinomial yang lebih panjang ditambah satu, dan baris sebanyak jumlah suku dalam polinomial yang lebih pendek ditambah satu.
Pada baris pertama tabel, tuliskan koefisien dari polinomial yang lebih panjang, dimulai dari koefisien suku dengan pangkat tertinggi.
Pada kolom pertama tabel, tuliskan koefisien dari polinomial yang lebih pendek, dimulai dari koefisien suku dengan pangkat tertinggi.
Kalikan koefisien pertama dari polinomial yang lebih pendek dengan koefisien pertama dari polinomial yang lebih panjang, dan tuliskan hasilnya di kolom kedua, baris pertama tabel.
Jumlahkan hasil kali dengan koefisien kedua dari polinomial yang lebih panjang, dan tuliskan hasilnya di kolom kedua, baris kedua tabel.
Ulangi langkah 5 dan 6 untuk setiap koefisien dari polinomial yang lebih pendek.
Hasil kali dari kedua polinomial akan terletak pada baris terakhir tabel, dengan koefisien dari suku dengan pangkat tertinggi berada di kolom paling kanan, dan koefisien dari suku dengan pangkat terendah berada di kolom paling kiri.

Contoh Soal Perkalian Polinomial dengan Metode Horner

Misalkan kita ingin mengalikan dua polinomial berikut:

(x^2 + 2x + 1) * (x + 3)

Berikut adalah langkah-langkah untuk mengalikan kedua polinomial tersebut dengan metode Horner:

Tuliskan kedua polinomial dalam bentuk baris horizontal, dengan koefisien dari setiap suku polinomial disusun berdasarkan pangkatnya:

(1 2 1) * (1 3)
Buat tabel dengan 4 kolom dan 3 baris:
| | 1 | 2 | 1 |
|—|—|—|—|
| 1 | | | |
| 3 | | | |
Tuliskan koefisien dari polinomial yang lebih panjang pada baris pertama tabel:
| | 1 | 2 | 1 |
|—|—|—|—|
| 1 | 1 | | |
| 3 | | | |
Tuliskan koefisien dari polinomial yang lebih pendek pada kolom pertama tabel:
| | 1 | 2 | 1 |
|—|—|—|—|
| 1 | 1 | | |
| 3 | 3 | | |
Kalikan koefisien pertama dari polinomial yang lebih pendek (1) dengan koefisien pertama dari polinomial yang lebih panjang (1), dan tuliskan hasilnya di kolom kedua, baris pertama tabel:
| | 1 | 2 | 1 |
|—|—|—|—|
| 1 | 1 | 1 | |
| 3 | 3 | | |
Jumlahkan hasil kali (1) dengan koefisien kedua dari polinomial yang lebih panjang (2), dan tuliskan hasilnya di kolom kedua, baris kedua tabel:
| | 1 | 2 | 1 |
|—|—|—|—|
| 1 | 1 | 1 | |
| 3 | 3 | 5 | |
Kalikan koefisien kedua dari polinomial yang lebih pendek (3) dengan koefisien pertama dari polinomial yang lebih panjang (1), dan tuliskan hasilnya di kolom ketiga, baris pertama tabel:
| | 1 | 2 | 1 |
|—|—|—|—|
| 1 | 1 | 1 | 3 |
| 3 | 3 | 5 | |
Jumlahkan hasil kali (3) dengan koefisien kedua dari polinomial yang lebih panjang (2), dan tuliskan hasilnya di kolom ketiga, baris kedua tabel:
| | 1 | 2 | 1 |
|—|—|—|—|
| 1 | 1 | 1 | 3 |
| 3 | 3 | 5 | 8 |
Kalikan koefisien kedua dari polinomial yang lebih pendek (3) dengan koefisien ketiga dari polinomial yang lebih panjang (1), dan tuliskan hasilnya di kolom keempat, baris pertama tabel:
| | 1 | 2 | 1 |
|—|—|—|—|
| 1 | 1 | 1 | 3 |
| 3 | 3 | 5 | 8 | 3 |
Jumlahkan hasil kali (3) dengan koefisien ketiga dari polinomial yang lebih panjang (1), dan tuliskan hasilnya di kolom keempat, baris kedua tabel:
| | 1 | 2 | 1 |
|—|—|—|—|
| 1 | 1 | 1 | 3 |
| 3 | 3 | 5 | 8 | 3 |
Hasil kali dari kedua polinomial adalah:

x^3 + 5x^2 + 8x + 3

Perkalian Polinomial dengan Metode Grafik

Perkalian polinomial merupakan operasi matematika yang melibatkan perkalian dua atau lebih polinomial. Metode grafik merupakan salah satu cara untuk menyelesaikan perkalian polinomial secara visual. Metode ini sangat membantu dalam memahami konsep perkalian polinomial dan mempermudah dalam menyelesaikan soal-soal yang berkaitan dengan perkalian polinomial.

Metode Grafik dalam Perkalian Polinomial

Metode grafik dalam perkalian polinomial memanfaatkan representasi visual dari polinomial dalam bentuk diagram. Diagram tersebut kemudian digunakan untuk menentukan hasil perkalian dari kedua polinomial.

Langkah-langkah Metode Grafik dalam Perkalian Polinomial

Berikut adalah langkah-langkah dalam melakukan perkalian polinomial dengan metode grafik:

Buatlah diagram persegi panjang dengan jumlah kolom sesuai dengan jumlah suku pada polinomial pertama dan jumlah baris sesuai dengan jumlah suku pada polinomial kedua.
Tuliskan setiap suku dari polinomial pertama di bagian atas kolom dan setiap suku dari polinomial kedua di bagian sisi kiri baris.
Isi setiap kotak pada diagram dengan hasil perkalian suku yang bersesuaian pada kolom dan baris tersebut.
Jumlahkan semua hasil perkalian yang berada pada diagonal yang sama. Hasil penjumlahan ini merupakan suku-suku dari polinomial hasil perkalian.

Contoh Soal Perkalian Polinomial dengan Metode Grafik

Misalkan kita ingin mengalikan polinomial (x + 2) dengan (x – 1).

Buatlah diagram persegi panjang dengan 2 kolom (sesuai dengan jumlah suku pada (x + 2)) dan 2 baris (sesuai dengan jumlah suku pada (x – 1)).
Tuliskan suku-suku dari (x + 2) di bagian atas kolom (x dan 2) dan suku-suku dari (x – 1) di bagian sisi kiri baris (x dan -1).
Isi setiap kotak dengan hasil perkalian suku yang bersesuaian pada kolom dan baris tersebut. Misalnya, kotak pertama berisi hasil perkalian x dengan x, yaitu x². Kotak kedua berisi hasil perkalian x dengan -1, yaitu -x. Kotak ketiga berisi hasil perkalian 2 dengan x, yaitu 2x. Kotak keempat berisi hasil perkalian 2 dengan -1, yaitu -2.
Jumlahkan semua hasil perkalian yang berada pada diagonal yang sama. Diagonal pertama berisi x². Diagonal kedua berisi -x + 2x = x. Diagonal ketiga berisi -2.

Oleh karena itu, hasil perkalian dari (x + 2) dengan (x – 1) adalah x² + x – 2.

Ulasan Penutup

Perkalian polinomial merupakan konsep penting dalam matematika yang memiliki banyak aplikasi di berbagai bidang. Dengan memahami berbagai metode perkalian polinomial dan melatih diri dengan contoh soal, Anda akan mampu menyelesaikan berbagai masalah dengan mudah dan percaya diri. Jangan ragu untuk terus belajar dan mengeksplorasi dunia matematika yang luas dan menarik ini!

Contoh Soal Perkalian Polinomial Beserta Jawabannya: Pelajari dan Kuasai!

Pengertian Perkalian Polinomial