Matematika, ilmu yang sering dianggap menakutkan oleh banyak orang, sebenarnya menyimpan keindahan tersendiri ketika kita memahami konsepnya dengan baik. Indikator Pemahaman Konsep Matematika menjadi kunci untuk membuka pintu menuju pemahaman yang lebih mendalam tentang dunia angka dan rumus. Bayangkan, jika Anda mampu memahami konsep dasar matematika, Anda akan dapat menyelesaikan berbagai masalah dengan lebih mudah, bahkan menemukan solusi yang kreatif dan inovatif.
Memahami konsep matematika berarti tidak hanya menghafal rumus dan prosedur, tetapi juga memahami makna di baliknya. Hal ini memungkinkan kita untuk menerapkan pengetahuan matematika dalam berbagai situasi dan memecahkan masalah dengan lebih fleksibel. Dengan memahami konsep, kita dapat membangun pondasi yang kuat untuk mempelajari matematika lebih lanjut dan mencapai hasil yang lebih optimal.
Pengertian Pemahaman Konsep Matematika
Pemahaman konsep matematika adalah kemampuan seseorang untuk memahami dan menguasai konsep-konsep matematika secara mendalam, tidak hanya sekedar menghafal rumus atau prosedur. Orang yang memiliki pemahaman konsep matematika yang kuat dapat memahami hubungan antara konsep-konsep tersebut, dapat menerapkan konsep-konsep tersebut dalam berbagai situasi, dan dapat memecahkan masalah matematika dengan lebih mudah.
Contoh Pemahaman Konsep Matematika
Misalnya, untuk memahami konsep perkalian, seseorang tidak hanya perlu menghafal tabel perkalian. Ia harus memahami bahwa perkalian merupakan operasi yang menunjukkan pengulangan penjumlahan. Misalnya, 3 x 4 sama dengan 3 + 3 + 3 + 3. Dengan memahami konsep ini, seseorang dapat lebih mudah memahami dan menyelesaikan masalah perkalian yang lebih kompleks.
Perbedaan Pemahaman Konsep dan Prosedural
Pemahaman konsep matematika berbeda dengan pemahaman prosedural. Pemahaman prosedural adalah kemampuan seseorang untuk menyelesaikan masalah matematika dengan mengikuti langkah-langkah tertentu tanpa memahami konsep di baliknya. Misalnya, seseorang mungkin dapat menyelesaikan soal persamaan linear dengan mengikuti langkah-langkah yang diajarkan tanpa memahami konsep persamaan linear itu sendiri.
Orang yang hanya memiliki pemahaman prosedural mungkin kesulitan dalam menyelesaikan masalah matematika yang tidak familiar atau dalam menerapkan konsep matematika dalam situasi baru. Sebaliknya, orang yang memiliki pemahaman konsep matematika yang kuat dapat menyelesaikan masalah matematika dengan lebih fleksibel dan kreatif, karena mereka memahami konsep di baliknya.
Karakteristik Seseorang dengan Pemahaman Konsep Matematika yang Kuat
- Dapat menjelaskan konsep matematika dengan kata-kata mereka sendiri.
- Dapat memberikan contoh konkret dari konsep matematika yang dipelajari.
- Dapat menghubungkan konsep matematika yang dipelajari dengan konsep matematika lainnya.
- Dapat menerapkan konsep matematika dalam berbagai situasi.
- Dapat memecahkan masalah matematika dengan lebih mudah dan kreatif.
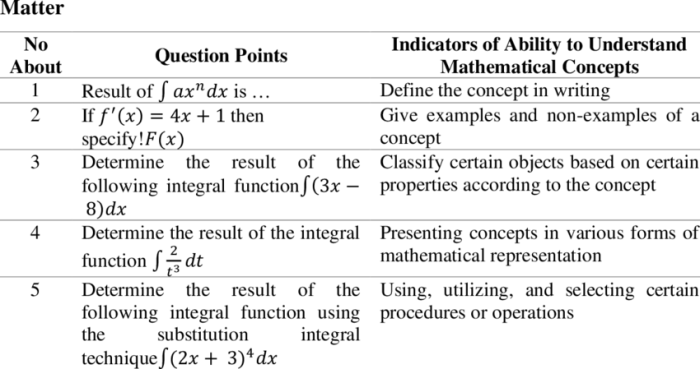
Indikator Pemahaman Konsep Matematika
Pemahaman konsep matematika merupakan hal yang sangat penting dalam pembelajaran matematika. Pemahaman konsep matematika bukan hanya sekedar menghafal rumus atau prosedur, tetapi juga tentang bagaimana siswa dapat menghubungkan konsep tersebut dengan konsep lainnya, menerapkannya dalam berbagai situasi, dan menjelaskan konsep tersebut dengan kata-kata mereka sendiri.
Identifikasi Indikator Pemahaman Konsep Matematika Berdasarkan Teori Belajar
Untuk mengidentifikasi indikator pemahaman konsep matematika, kita dapat merujuk pada beberapa teori belajar. Beberapa teori belajar yang dapat digunakan sebagai acuan adalah:
- Teori Konstruktivisme: Teori ini menyatakan bahwa pemahaman dibangun oleh siswa sendiri melalui pengalaman dan interaksi dengan lingkungan sekitar. Indikator pemahaman konsep matematika berdasarkan teori ini meliputi kemampuan siswa untuk membangun pemahaman sendiri, menghubungkan konsep baru dengan konsep yang sudah diketahui, dan menggunakan konsep tersebut dalam berbagai situasi.
- Teori Ausubel: Teori ini menekankan pentingnya pembelajaran yang bermakna. Indikator pemahaman konsep matematika berdasarkan teori ini meliputi kemampuan siswa untuk memahami makna konsep, menghubungkan konsep dengan pengetahuan sebelumnya, dan menggunakan konsep tersebut untuk memecahkan masalah.
- Teori Vygotsky: Teori ini menekankan pentingnya peran sosial dalam pembelajaran. Indikator pemahaman konsep matematika berdasarkan teori ini meliputi kemampuan siswa untuk berkolaborasi dengan orang lain dalam memahami konsep, menggunakan bahasa untuk menjelaskan konsep, dan menggunakan alat bantu untuk memahami konsep.
Tabel Indikator Pemahaman Konsep Matematika
Berikut adalah tabel yang berisi indikator pemahaman konsep matematika, deskripsi, dan contoh observasi:
| Indikator | Deskripsi | Contoh Observasi |
|---|---|---|
| Menjelaskan konsep dengan kata-kata sendiri | Siswa mampu menjelaskan konsep matematika dengan kata-kata mereka sendiri, tanpa hanya mengulang definisi dari buku teks atau guru. | Siswa dapat menjelaskan konsep “luas persegi panjang” dengan mengatakan, “Luas persegi panjang adalah ukuran ruang yang ditempati oleh persegi panjang, yang dapat dihitung dengan mengalikan panjang dan lebarnya.” |
| Memberikan contoh dan non-contoh konsep | Siswa mampu memberikan contoh dan non-contoh dari konsep matematika yang sedang dipelajari. | Siswa dapat memberikan contoh dari “bilangan prima” seperti 2, 3, 5, 7, dan 11. Mereka juga dapat memberikan non-contoh seperti 4, 6, 8, dan 9. |
| Menerapkan konsep dalam berbagai situasi | Siswa mampu menerapkan konsep matematika dalam berbagai situasi, baik dalam konteks matematika maupun dalam kehidupan sehari-hari. | Siswa dapat menerapkan konsep “persentase” untuk menghitung diskon di toko, atau untuk menghitung nilai ujian. |
| Menghubungkan konsep dengan konsep lain | Siswa mampu menghubungkan konsep matematika yang sedang dipelajari dengan konsep matematika lainnya yang sudah dipelajari sebelumnya. | Siswa dapat menghubungkan konsep “luas” dengan konsep “keliling” untuk menghitung luas dan keliling bangun datar. |
| Memecahkan masalah yang melibatkan konsep | Siswa mampu memecahkan masalah yang melibatkan konsep matematika yang sedang dipelajari. | Siswa dapat memecahkan masalah yang meminta mereka untuk mencari luas persegi panjang, atau untuk menghitung persentase keuntungan dari penjualan. |
| Menjelaskan hubungan antara konsep dan representasi | Siswa mampu menjelaskan hubungan antara konsep matematika dengan representasi yang berbeda, seperti gambar, diagram, grafik, atau simbol. | Siswa dapat menjelaskan hubungan antara konsep “fraksi” dengan representasi gambar, diagram, atau simbol. |
Contoh Pengukuran Indikator Pemahaman Konsep Matematika
Indikator pemahaman konsep matematika dapat diukur melalui berbagai metode, seperti:
- Tes tertulis: Tes tertulis dapat digunakan untuk mengukur kemampuan siswa dalam menjelaskan konsep, memberikan contoh, dan memecahkan masalah. Contohnya, soal tes dapat meminta siswa untuk menjelaskan konsep “faktor persekutuan terbesar” dengan kata-kata mereka sendiri, atau untuk menyelesaikan soal cerita yang melibatkan konsep “persentase”.
- Observasi: Observasi dapat digunakan untuk mengukur kemampuan siswa dalam berdiskusi, berkolaborasi, dan menggunakan alat bantu dalam memahami konsep. Contohnya, guru dapat mengamati siswa saat mereka bekerja dalam kelompok untuk menyelesaikan masalah, atau saat mereka menggunakan kalkulator untuk menyelesaikan soal.
- Portofolio: Portofolio dapat digunakan untuk mengumpulkan karya siswa yang menunjukkan pemahaman konsep matematika mereka. Contohnya, portofolio dapat berisi catatan siswa, hasil pekerjaan kelompok, dan hasil tes.
Aspek-Aspek Pemahaman Konsep Matematika

Memahami konsep matematika bukan sekadar menghafal rumus atau prosedur. Ada beberapa aspek penting yang saling terkait dan membentuk pemahaman yang utuh.
Pengetahuan Faktual
Aspek pertama ini merupakan pondasi pemahaman konsep. Ini mencakup pengetahuan dasar tentang fakta, definisi, simbol, dan terminologi dalam matematika. Misalnya, memahami bahwa “persegi panjang” adalah bangun datar dengan empat sisi dan empat sudut siku-siku, atau memahami simbol “+” untuk penjumlahan.
- Contoh: Mengetahui bahwa “1 meter” sama dengan “100 sentimeter” merupakan pengetahuan faktual tentang satuan pengukuran.
Pemahaman Hubungan Antar Konsep
Memahami bagaimana konsep-konsep dalam matematika saling berhubungan sangat penting. Ini berarti mampu melihat hubungan antara konsep yang berbeda dan bagaimana satu konsep dapat menjelaskan atau dijelaskan oleh konsep lainnya.
- Contoh: Memahami bahwa luas persegi panjang dihitung dengan mengalikan panjang dan lebar, dan bahwa rumus ini terkait dengan konsep penjumlahan dan perkalian.
Penerapan Konsep dalam Situasi Baru
Pemahaman konsep yang baik ditunjukkan dengan kemampuan menerapkan konsep dalam situasi baru yang belum pernah dipelajari sebelumnya. Ini menunjukkan bahwa seseorang benar-benar memahami konsep dan tidak hanya menghafalnya.
- Contoh: Seorang siswa yang memahami konsep persamaan linear dapat menerapkannya untuk menyelesaikan masalah yang melibatkan hubungan antara harga dan jumlah barang yang dibeli.
Kemampuan Menjelaskan Konsep dengan Bahasa Sendiri
Aspek terakhir ini menunjukkan bahwa seseorang benar-benar memahami konsep dan dapat mengomunikasikannya dengan jelas dan ringkas. Ini berarti mampu menjelaskan konsep dengan kata-kata sendiri, bukan hanya mengulang definisi yang sudah ada.
- Contoh: Seorang siswa yang memahami konsep “fungsi” dapat menjelaskan dengan kata-kata sendiri bahwa fungsi adalah aturan yang menghubungkan setiap input dengan output yang unik.
Strategi Meningkatkan Pemahaman Konsep Matematika
Pemahaman konsep matematika sangat penting untuk menguasai materi dan memecahkan masalah. Tanpa pemahaman yang kuat, siswa mungkin kesulitan dalam menerapkan konsep matematika dalam situasi yang berbeda. Oleh karena itu, penting bagi guru dan siswa untuk menerapkan strategi yang efektif untuk meningkatkan pemahaman konsep matematika.
Strategi Pembelajaran Efektif
Beberapa strategi pembelajaran dapat membantu siswa meningkatkan pemahaman konsep matematika. Strategi ini dapat diimplementasikan dalam berbagai konteks pembelajaran, baik di kelas maupun di rumah.
- Belajar aktif: Alih-alih hanya mendengarkan penjelasan guru, siswa dapat terlibat aktif dalam pembelajaran dengan bertanya, berdiskusi, dan menyelesaikan masalah secara mandiri. Mereka dapat mencoba mengajarkan konsep kepada teman sekelas atau membuat catatan sendiri dengan kata-kata mereka sendiri.
- Pembuatan model: Pembuatan model membantu siswa memvisualisasikan konsep matematika abstrak. Mereka dapat menggunakan benda-benda nyata, gambar, atau diagram untuk merepresentasikan konsep dan memahami hubungan antar konsep.
- Pembelajaran kolaboratif: Berdiskusi dengan teman sekelas tentang konsep matematika dapat membantu siswa memahami perspektif yang berbeda dan mengidentifikasi kesalahpahaman mereka sendiri. Melalui kerja sama, mereka dapat saling membantu dan belajar dari satu sama lain.
- Pembelajaran berbasis proyek: Proyek yang menantang siswa untuk menerapkan konsep matematika dalam situasi nyata dapat membantu mereka memahami relevansi dan aplikasi konsep tersebut. Mereka dapat bekerja dalam kelompok untuk merancang solusi untuk masalah dunia nyata yang melibatkan konsep matematika.
Contoh Aktivitas Pembelajaran
Aktivitas pembelajaran yang dirancang dengan baik dapat mendorong siswa untuk membangun pemahaman konsep matematika secara mendalam. Berikut beberapa contoh aktivitas pembelajaran yang dapat diterapkan:
- Menghubungkan konsep: Siswa dapat diminta untuk menemukan hubungan antara konsep matematika yang berbeda. Misalnya, mereka dapat mendemonstrasikan bagaimana konsep pecahan berhubungan dengan konsep desimal dan persentase.
- Menciptakan cerita: Siswa dapat membuat cerita atau skenario yang melibatkan konsep matematika tertentu. Ini dapat membantu mereka memahami aplikasi konsep tersebut dalam konteks kehidupan nyata.
- Membuat permainan: Siswa dapat merancang permainan yang melibatkan konsep matematika tertentu. Melalui proses pembuatan permainan, mereka dapat memahami konsep tersebut secara lebih dalam dan juga mengembangkan keterampilan berpikir kritis dan kreatif.
- Menyelesaikan masalah terbuka: Masalah terbuka tidak memiliki satu jawaban yang benar. Siswa harus menggunakan pemahaman konsep mereka untuk menemukan solusi yang mungkin dan menguji solusi tersebut. Ini mendorong mereka untuk berpikir kritis dan kreatif dalam memecahkan masalah.
Penggunaan Media Pembelajaran
Media pembelajaran dapat membantu meningkatkan pemahaman konsep matematika dengan memberikan representasi visual, interaktif, dan menarik. Penggunaan media pembelajaran yang tepat dapat meningkatkan keterlibatan siswa dan membantu mereka memahami konsep yang sulit.
- Video pembelajaran: Video pembelajaran dapat memberikan penjelasan yang jelas dan visual tentang konsep matematika. Video dapat diintegrasikan dengan simulasi dan animasi untuk meningkatkan pemahaman siswa.
- Simulasi komputer: Simulasi komputer memungkinkan siswa untuk bereksperimen dengan konsep matematika dan melihat hasilnya secara langsung. Simulasi dapat membantu siswa memahami hubungan antar konsep dan mengembangkan intuisi matematis.
- Perangkat lunak pendidikan: Perangkat lunak pendidikan dapat menyediakan berbagai aktivitas pembelajaran yang menarik dan interaktif. Perangkat lunak ini dapat digunakan untuk mengajarkan konsep matematika, melatih keterampilan memecahkan masalah, dan memberikan umpan balik kepada siswa.
- Aplikasi mobile: Aplikasi mobile dapat memberikan akses mudah ke berbagai sumber belajar matematika, termasuk latihan, permainan, dan video pembelajaran. Aplikasi ini dapat membantu siswa belajar di mana saja dan kapan saja.
Contoh Penerapan Indikator Pemahaman Konsep Matematika
Indikator pemahaman konsep matematika berperan penting dalam menilai kemampuan siswa dalam memahami konsep matematika. Indikator ini membantu guru dalam mengidentifikasi tingkat pemahaman siswa, baik secara individual maupun secara keseluruhan kelas. Dengan memahami indikator ini, guru dapat merancang pembelajaran yang efektif dan menuntun siswa untuk mencapai pemahaman yang lebih dalam.
Penerapan Indikator dalam Pembelajaran
Berikut beberapa contoh penerapan indikator pemahaman konsep matematika dalam pembelajaran:
- Menjelaskan konsep dengan kata-kata sendiri. Misalnya, setelah mempelajari konsep persamaan linear, siswa diminta untuk menjelaskan konsep tersebut dengan kata-kata mereka sendiri. Dengan demikian, guru dapat menilai apakah siswa memahami konsep secara mendalam atau hanya menghafal rumus.
- Memberikan contoh dan bukan contoh dari konsep. Guru dapat meminta siswa untuk memberikan contoh dan bukan contoh dari konsep yang sedang dipelajari. Misalnya, setelah mempelajari konsep segitiga, siswa diminta untuk memberikan contoh segitiga dan bukan contoh segitiga. Dengan demikian, guru dapat menilai apakah siswa dapat mengidentifikasi ciri-ciri utama dari konsep tersebut.
- Menerapkan konsep dalam konteks yang berbeda. Guru dapat memberikan soal-soal yang mengharuskan siswa untuk menerapkan konsep yang dipelajari dalam konteks yang berbeda. Misalnya, setelah mempelajari konsep luas persegi panjang, siswa diminta untuk menghitung luas taman berbentuk persegi panjang yang memiliki ukuran tertentu. Dengan demikian, guru dapat menilai apakah siswa dapat menghubungkan konsep dengan situasi nyata.
Contoh Soal Pemahaman Konsep, Indikator pemahaman konsep matematika
Berikut contoh soal yang mengukur pemahaman konsep matematika pada topik persamaan linear:
Persamaan linear adalah persamaan yang memiliki bentuk ax + by = c, dengan a, b, dan c adalah konstanta, dan x dan y adalah variabel.
Soal
Sebuah toko menjual dua jenis minuman, yaitu jus jeruk dan teh manis. Harga satu gelas jus jeruk adalah Rp5.000 dan harga satu gelas teh manis adalah Rp3.000. Jika seorang pembeli membeli 3 gelas jus jeruk dan 2 gelas teh manis, berapa total uang yang harus dibayarkan pembeli tersebut?
Contoh Jawaban Siswa
- Siswa A: Total uang yang harus dibayarkan adalah Rp5.000 x 3 + Rp3.000 x 2 = Rp15.000 + Rp6.000 = Rp21.000.
Pemahaman: Siswa A memahami konsep persamaan linear dan dapat menerapkannya untuk menyelesaikan masalah. Siswa A juga dapat menghitung dengan benar.
- Siswa B: Total uang yang harus dibayarkan adalah Rp5.000 x 2 + Rp3.000 x 3 = Rp10.000 + Rp9.000 = Rp19.000.
Pemahaman: Siswa B memahami konsep persamaan linear, namun salah dalam menerapkannya. Siswa B keliru dalam menghitung jumlah gelas jus jeruk dan teh manis.
- Siswa C: Saya tidak tahu cara menyelesaikannya.
Pemahaman: Siswa C belum memahami konsep persamaan linear dan tidak dapat menerapkannya untuk menyelesaikan masalah.
Ringkasan Terakhir

Pemahaman konsep matematika merupakan fondasi yang penting dalam pembelajaran matematika. Dengan memahami konsep, kita dapat menguasai matematika dengan lebih baik dan memanfaatkannya dalam berbagai aspek kehidupan. Melalui penerapan indikator pemahaman konsep, kita dapat mengukur dan meningkatkan pemahaman matematika, sehingga pembelajaran menjadi lebih bermakna dan menyenangkan.







