Contoh soal rangkaian rlc – Rangkaian RLC, yang terdiri dari resistor (R), induktor (L), dan kapasitor (C), merupakan komponen penting dalam berbagai sistem elektronik. Dari filter yang menyaring frekuensi tertentu hingga osilator yang menghasilkan sinyal periodik, rangkaian RLC memainkan peran kunci dalam mengendalikan aliran arus dan tegangan.
Melalui contoh soal, kita akan menjelajahi konsep-konsep dasar rangkaian RLC, seperti impedansi, resonansi, dan analisis respon frekuensi. Dengan memahami prinsip-prinsip ini, Anda akan dapat menganalisis dan merancang rangkaian RLC untuk berbagai aplikasi praktis.
Pengertian Rangkaian RLC: Contoh Soal Rangkaian Rlc
Rangkaian RLC adalah sebuah rangkaian listrik yang terdiri dari resistor (R), induktor (L), dan kapasitor (C). Rangkaian ini dapat dihubungkan secara seri atau paralel. Rangkaian RLC memiliki berbagai aplikasi penting dalam berbagai bidang, termasuk elektronik, telekomunikasi, dan sistem kontrol.
Fungsi Komponen dalam Rangkaian RLC
Rangkaian RLC terdiri dari tiga komponen utama yang memiliki peran penting dalam perilaku rangkaian. Ketiga komponen tersebut adalah:
- Resistor (R): Resistor adalah komponen yang menghambat aliran arus listrik. Resistor mengubah energi listrik menjadi energi panas. Nilai hambatan resistor diukur dalam satuan ohm (Ω).
- Induktor (L): Induktor adalah komponen yang menyimpan energi dalam bentuk medan magnet. Induktor terdiri dari kumparan kawat yang dililitkan pada inti magnetik. Nilai induktansi induktor diukur dalam satuan henry (H). Induktor memiliki sifat untuk menentang perubahan arus listrik.
- Kapasitor (C): Kapasitor adalah komponen yang menyimpan energi dalam bentuk medan listrik. Kapasitor terdiri dari dua pelat konduktor yang dipisahkan oleh bahan isolator (dielektrik). Nilai kapasitansi kapasitor diukur dalam satuan farad (F). Kapasitor memiliki sifat untuk menentang perubahan tegangan listrik.
Contoh Sederhana Rangkaian RLC
Berikut adalah contoh sederhana rangkaian RLC:
- Rangkaian RLC Seri: Pada rangkaian RLC seri, resistor, induktor, dan kapasitor dihubungkan secara berurutan dalam satu jalur. Arus yang mengalir melalui setiap komponen adalah sama.
- Rangkaian RLC Paralel: Pada rangkaian RLC paralel, resistor, induktor, dan kapasitor dihubungkan secara terpisah pada titik yang sama. Tegangan pada setiap komponen adalah sama.
Jenis-jenis Rangkaian RLC
Terdapat beberapa jenis rangkaian RLC, yaitu:
- Rangkaian RLC Seri: Rangkaian RLC seri adalah rangkaian yang memiliki resistor, induktor, dan kapasitor yang dihubungkan secara seri. Rangkaian ini memiliki satu jalur arus yang sama untuk ketiga komponen.
- Rangkaian RLC Paralel: Rangkaian RLC paralel adalah rangkaian yang memiliki resistor, induktor, dan kapasitor yang dihubungkan secara paralel. Rangkaian ini memiliki tiga jalur arus yang terpisah untuk setiap komponen.
- Rangkaian RLC Resonansi: Rangkaian RLC resonansi adalah rangkaian yang memiliki frekuensi resonansi tertentu. Pada frekuensi resonansi, impedansi rangkaian minimum dan arus maksimum. Rangkaian ini banyak digunakan dalam filter, osilator, dan amplifier.
Karakteristik Rangkaian RLC
Rangkaian RLC, yang terdiri dari resistor (R), induktor (L), dan kapasitor (C), memiliki karakteristik unik yang dipengaruhi oleh interaksi komponen-komponennya. Salah satu konsep penting dalam memahami perilaku rangkaian RLC adalah impedansi.
Impedansi dalam Rangkaian RLC
Impedansi dalam rangkaian RLC adalah ukuran total perlawanan terhadap arus bolak-balik (AC). Berbeda dengan resistansi yang hanya mempertimbangkan hambatan terhadap arus searah (DC), impedansi memperhitungkan juga pengaruh reaktansi induktif dan kapasitif yang muncul akibat perubahan arus dan tegangan AC.
Contoh soal rangkaian RLC bisa membantu kamu memahami konsep dasar rangkaian arus bolak-balik. Nah, kalau kamu lagi belajar buat ujian masuk KPU, kamu bisa coba cari contoh soal CAT KPU PDF untuk latihan. Mirip seperti soal rangkaian RLC, soal CAT KPU juga punya pola dan rumus yang perlu kamu kuasai.
Semoga latihan soal ini bisa bantu kamu sukses di ujian ya!
Rumus Impedansi Rangkaian RLC
Rumus impedansi untuk rangkaian RLC seri dan paralel berbeda, karena cara komponen-komponen tersebut tersusun dalam rangkaian. Berikut adalah tabel yang merangkum rumus impedansi untuk kedua konfigurasi tersebut:
| Konfigurasi | Rumus Impedansi |
|---|---|
| Seri | Z = √(R² + (XL – XC)²) |
| Paralel | 1/Z = √(1/R² + (1/XL – 1/XC)²) |
Faktor yang Mempengaruhi Impedansi Rangkaian RLC
Impedansi rangkaian RLC dipengaruhi oleh beberapa faktor, antara lain:
- Nilai resistansi (R): Semakin besar nilai resistansi, semakin tinggi impedansi. Ini karena resistansi merupakan hambatan langsung terhadap aliran arus.
- Nilai induktansi (L): Semakin besar nilai induktansi, semakin tinggi reaktansi induktif (XL), yang pada gilirannya meningkatkan impedansi. Reaktansi induktif merupakan perlawanan terhadap perubahan arus, yang semakin besar pada frekuensi yang lebih tinggi.
- Nilai kapasitansi (C): Semakin besar nilai kapasitansi, semakin rendah reaktansi kapasitif (XC), yang pada gilirannya menurunkan impedansi. Reaktansi kapasitif merupakan perlawanan terhadap perubahan tegangan, yang semakin kecil pada frekuensi yang lebih tinggi.
- Frekuensi arus (f): Frekuensi arus berpengaruh terhadap reaktansi induktif dan kapasitif. Semakin tinggi frekuensi, semakin tinggi XL dan semakin rendah XC. Akibatnya, impedansi rangkaian RLC juga dipengaruhi oleh frekuensi.
Analisis Rangkaian RLC
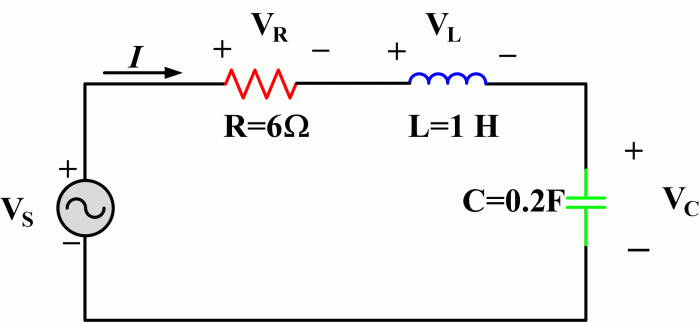
Rangkaian RLC merupakan kombinasi dari resistor (R), induktor (L), dan kapasitor (C) yang terhubung secara seri atau paralel. Analisis rangkaian RLC bertujuan untuk memahami perilaku rangkaian, seperti arus, tegangan, dan daya, serta bagaimana karakteristik rangkaian dipengaruhi oleh perubahan nilai komponen.
Langkah-langkah Analisis Rangkaian RLC, Contoh soal rangkaian rlc
Analisis rangkaian RLC melibatkan beberapa langkah yang terstruktur untuk mendapatkan pemahaman yang komprehensif tentang perilaku rangkaian. Berikut adalah flowchart langkah-langkah analisis rangkaian RLC:
- Tentukan Jenis Rangkaian: Identifikasi apakah rangkaian RLC terhubung secara seri atau paralel. Jenis rangkaian menentukan bagaimana komponen-komponen saling mempengaruhi.
- Tentukan Nilai Komponen: Tentukan nilai resistansi (R), induktansi (L), dan kapasitansi (C) dari masing-masing komponen. Nilai-nilai ini akan menentukan karakteristik rangkaian.
- Hitung Impedansi Rangkaian: Impedansi (Z) adalah resistansi total rangkaian RLC, yang menggabungkan resistansi, reaktansi induktif, dan reaktansi kapasitif. Impedansi dihitung dengan rumus:
- Hitung Arus Rangkaian: Arus (I) yang mengalir dalam rangkaian RLC dapat dihitung dengan menggunakan hukum Ohm, yaitu:
- Hitung Tegangan pada Setiap Komponen: Tegangan pada resistor (VR), induktor (VL), dan kapasitor (VC) dapat dihitung dengan menggunakan hukum Ohm dan reaktansi masing-masing komponen.
VR = IR, VL = IXL, VC = IXC
- Hitung Daya Rangkaian: Daya (P) yang diserap oleh rangkaian RLC dapat dihitung dengan rumus:
- Analisis Frekuensi Resonansi: Frekuensi resonansi (fr) adalah frekuensi di mana reaktansi induktif (XL) sama dengan reaktansi kapasitif (XC). Pada frekuensi resonansi, impedansi rangkaian minimum dan arus maksimum.
fr = 1/(2π√(LC))
- Analisis Faktor Daya: Faktor daya (PF) adalah rasio daya aktif (P) terhadap daya semu (S). Faktor daya menunjukkan seberapa efisien daya digunakan dalam rangkaian.
PF = P/S = R/Z
Z = √(R² + (XL – XC)²)
I = V/Z
P = I²R
Cara Menghitung Arus, Tegangan, dan Daya
Berikut adalah contoh perhitungan arus, tegangan, dan daya pada rangkaian RLC seri dengan nilai komponen R = 100 Ω, L = 10 mH, C = 10 μF, dan tegangan sumber V = 10 V pada frekuensi f = 50 Hz:
- Hitung Reaktansi Induktif (XL):
- Hitung Reaktansi Kapasitif (XC):
- Hitung Impedansi (Z):
- Hitung Arus (I):
- Hitung Tegangan pada Resistor (VR):
- Hitung Tegangan pada Induktor (VL):
- Hitung Tegangan pada Kapasitor (VC):
- Hitung Daya (P):
XL = 2πfL = 2π(50 Hz)(10 mH) = 3.14 Ω
XC = 1/(2πfC) = 1/(2π(50 Hz)(10 μF)) = 318.31 Ω
Z = √(R² + (XL – XC)²) = √(100² + (3.14 – 318.31)²) = 317.5 Ω
I = V/Z = 10 V / 317.5 Ω = 0.0315 A
VR = IR = (0.0315 A)(100 Ω) = 3.15 V
VL = IXL = (0.0315 A)(3.14 Ω) = 0.0988 V
VC = IXC = (0.0315 A)(318.31 Ω) = 10.05 V
P = I²R = (0.0315 A)²(100 Ω) = 0.0992 W
Pengaruh Perubahan Nilai Komponen
Perubahan nilai komponen R, L, dan C akan memengaruhi karakteristik rangkaian RLC. Berikut adalah beberapa pengaruh yang perlu diperhatikan:
- Perubahan Resistor (R):
- Meningkatkan nilai resistansi (R) akan mengurangi arus dalam rangkaian dan meningkatkan daya yang diserap oleh resistor.
- Menurunkan nilai resistansi (R) akan meningkatkan arus dalam rangkaian dan mengurangi daya yang diserap oleh resistor.
- Perubahan Induktor (L):
- Meningkatkan nilai induktansi (L) akan meningkatkan reaktansi induktif (XL) dan mengurangi arus pada frekuensi rendah. Rangkaian akan lebih reaktif terhadap frekuensi rendah.
- Menurunkan nilai induktansi (L) akan mengurangi reaktansi induktif (XL) dan meningkatkan arus pada frekuensi rendah. Rangkaian akan kurang reaktif terhadap frekuensi rendah.
- Perubahan Kapasitor (C):
- Meningkatkan nilai kapasitansi (C) akan mengurangi reaktansi kapasitif (XC) dan meningkatkan arus pada frekuensi tinggi. Rangkaian akan lebih reaktif terhadap frekuensi tinggi.
- Menurunkan nilai kapasitansi (C) akan meningkatkan reaktansi kapasitif (XC) dan mengurangi arus pada frekuensi tinggi. Rangkaian akan kurang reaktif terhadap frekuensi tinggi.
Akhir Kata
Mempelajari rangkaian RLC membuka pintu menuju pemahaman yang lebih dalam tentang bagaimana komponen elektronik bekerja bersama untuk membentuk sistem yang kompleks. Dengan contoh soal yang diberikan, diharapkan Anda dapat mengaplikasikan pengetahuan ini untuk menyelesaikan masalah nyata dan mengembangkan inovasi baru di bidang teknik elektro.





