Contoh soal fungsi relasi – Relasi dan fungsi adalah konsep dasar dalam matematika yang sering kita jumpai dalam kehidupan sehari-hari. Mulai dari menentukan hubungan antara siswa dan kelasnya, hingga menghitung biaya pengiriman berdasarkan jarak tempuh, relasi dan fungsi berperan penting dalam berbagai situasi.
Dalam artikel ini, kita akan menjelajahi contoh soal fungsi relasi, mulai dari pengertian dasar hingga aplikasi praktisnya. Dengan memahami konsep ini, Anda akan dapat menganalisis hubungan antar variabel dan memecahkan berbagai masalah yang berkaitan dengan relasi dan fungsi.
Jenis-jenis Relasi
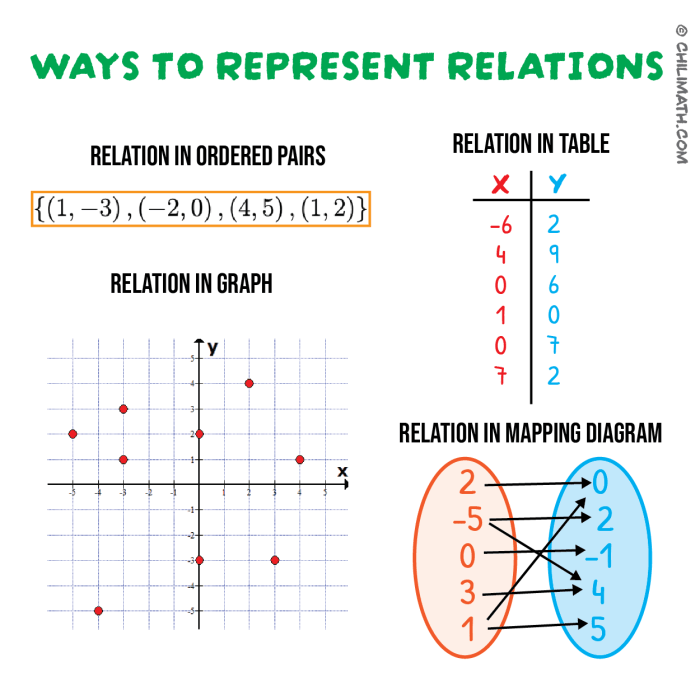
Relasi dalam matematika merupakan hubungan antara dua himpunan atau lebih. Hubungan ini dapat berupa hubungan satu-satu, banyak-satu, satu-banyak, atau banyak-banyak. Jenis relasi ini dapat dibedakan berdasarkan jumlah anggota pada himpunan domain (himpunan asal) dan kodomain (himpunan tujuan) yang memiliki pasangan.
Relasi Satu-satu
Relasi satu-satu (injektif) terjadi ketika setiap anggota pada himpunan domain memiliki pasangan yang unik dan berbeda pada himpunan kodomain. Artinya, tidak ada anggota kodomain yang dipasangkan dengan lebih dari satu anggota domain.
Contoh Soal
Misalnya, terdapat himpunan A = 1, 2, 3 dan himpunan B = a, b, c. Relasi R = (1, a), (2, b), (3, c) merupakan relasi satu-satu karena setiap anggota himpunan A dipasangkan dengan tepat satu anggota himpunan B.
Diagram Panah
Diagram panah untuk relasi satu-satu menunjukkan bahwa setiap anak panah dari himpunan A hanya menuju satu anggota himpunan B, dan tidak ada anggota B yang memiliki lebih dari satu anak panah yang menunjuk padanya.
Relasi Banyak-satu
Relasi banyak-satu (surjektif) terjadi ketika setiap anggota pada himpunan kodomain memiliki pasangan dari himpunan domain, tetapi satu anggota domain dapat dipasangkan dengan lebih dari satu anggota kodomain.
Contoh Soal
Misalnya, terdapat himpunan C = p, q, r dan himpunan D = x, y. Relasi S = (p, x), (q, x), (r, y) merupakan relasi banyak-satu karena anggota x pada himpunan D memiliki dua pasangan dari himpunan C, yaitu p dan q.
Diagram Panah
Diagram panah untuk relasi banyak-satu menunjukkan bahwa satu atau lebih anak panah dari himpunan C menuju satu anggota himpunan D, dan setiap anggota D memiliki minimal satu anak panah yang menunjuk padanya.
Relasi Satu-banyak
Relasi satu-banyak terjadi ketika setiap anggota pada himpunan domain hanya dipasangkan dengan satu anggota kodomain, tetapi satu anggota kodomain dapat dipasangkan dengan lebih dari satu anggota domain.
Contoh Soal
Misalnya, terdapat himpunan E = 1, 2 dan himpunan F = a, b, c. Relasi T = (1, a), (2, b), (2, c) merupakan relasi satu-banyak karena anggota 2 pada himpunan E dipasangkan dengan dua anggota F, yaitu b dan c.
Diagram Panah
Diagram panah untuk relasi satu-banyak menunjukkan bahwa setiap anak panah dari himpunan E hanya menuju satu anggota himpunan F, tetapi satu anggota F dapat memiliki lebih dari satu anak panah yang menunjuk padanya.
Relasi Banyak-banyak
Relasi banyak-banyak terjadi ketika beberapa anggota pada himpunan domain dipasangkan dengan beberapa anggota pada himpunan kodomain, dan sebaliknya.
Contoh Soal
Misalnya, terdapat himpunan G = 1, 2, 3 dan himpunan H = a, b, c. Relasi U = (1, a), (1, b), (2, b), (2, c), (3, c) merupakan relasi banyak-banyak karena anggota 1 pada himpunan G dipasangkan dengan dua anggota H, yaitu a dan b, dan anggota 2 pada himpunan G juga dipasangkan dengan dua anggota H, yaitu b dan c.
Diagram Panah
Diagram panah untuk relasi banyak-banyak menunjukkan bahwa beberapa anak panah dari himpunan G menuju beberapa anggota himpunan H, dan beberapa anak panah dari himpunan H menuju beberapa anggota himpunan G.
Domain, Kodomain, dan Range: Contoh Soal Fungsi Relasi
Dalam mempelajari relasi dan fungsi, kita seringkali menjumpai istilah domain, kodomain, dan range. Ketiga istilah ini merupakan konsep penting yang membantu kita memahami dan menganalisis relasi dan fungsi secara lebih mendalam. Mari kita bahas definisi dan contoh soal untuk menentukan domain, kodomain, dan range.
Contoh soal fungsi relasi memang penting untuk menguji pemahaman konsep. Soal-soal ini biasanya melibatkan penentuan domain, range, dan sifat relasi. Nah, kalau kamu sedang mencari contoh soal lain, kamu bisa cek contoh soal sejarah kelas 10 semester 1 yang juga bisa membantu kamu dalam memahami materi pelajaran.
Setelah berlatih dengan berbagai contoh soal, kamu pasti akan lebih siap menghadapi ujian fungsi relasi dan pelajaran sejarah lainnya.
Pengertian Domain, Kodomain, dan Range
Domain, kodomain, dan range merupakan bagian penting dalam memahami relasi dan fungsi. Ketiganya saling terkait dan membantu kita menentukan batasan dan hasil dari relasi atau fungsi tersebut.
- Domain: Domain adalah himpunan semua nilai input yang mungkin pada suatu relasi atau fungsi. Dengan kata lain, domain adalah himpunan semua nilai yang dapat digunakan sebagai masukan dalam relasi atau fungsi tersebut. Domain sering dilambangkan dengan huruf D.
- Kodomain: Kodomain adalah himpunan semua nilai output yang mungkin pada suatu relasi atau fungsi. Kodomain merupakan himpunan yang lebih luas dibandingkan dengan range, karena kodomain mencakup semua nilai yang mungkin dihasilkan, termasuk nilai yang tidak dihasilkan oleh relasi atau fungsi tersebut. Kodomain sering dilambangkan dengan huruf K.
- Range: Range adalah himpunan semua nilai output yang dihasilkan oleh suatu relasi atau fungsi. Dengan kata lain, range adalah himpunan semua nilai yang muncul sebagai hasil dari memasukan nilai domain ke dalam relasi atau fungsi tersebut. Range sering dilambangkan dengan huruf R.
Contoh Soal Penentuan Domain, Kodomain, dan Range
Berikut adalah contoh soal untuk menentukan domain, kodomain, dan range dari suatu relasi atau fungsi:
- Relasi: Misalkan terdapat relasi R dari himpunan A = 1, 2, 3 ke himpunan B = 4, 5, 6, yang didefinisikan sebagai: R = (1, 4), (2, 5), (3, 6).
- Domain (D) = 1, 2, 3
- Kodomain (K) = 4, 5, 6
- Range (R) = 4, 5, 6
- Fungsi: Misalkan terdapat fungsi f(x) = x^2 + 1, dengan domain x ∈ R (himpunan bilangan real).
- Domain (D) = R (himpunan bilangan real)
- Kodomain (K) = R (himpunan bilangan real)
- Range (R) = y | y ≥ 1 (himpunan bilangan real yang lebih besar atau sama dengan 1)
Tabel Domain, Kodomain, dan Range
Berikut adalah tabel yang menunjukkan domain, kodomain, dan range dari beberapa contoh relasi dan fungsi:
| Contoh | Domain (D) | Kodomain (K) | Range (R) |
|---|---|---|---|
| Relasi R = (1, 2), (2, 3), (3, 4) | 1, 2, 3 | 2, 3, 4 | 2, 3, 4 |
| Fungsi f(x) = 2x + 1 | R (himpunan bilangan real) | R (himpunan bilangan real) | R (himpunan bilangan real) |
| Fungsi g(x) = x^2 | R (himpunan bilangan real) | R (himpunan bilangan real) | y | y ≥ 0 (himpunan bilangan real yang lebih besar atau sama dengan 0) |
Fungsi Komposisi
Fungsi komposisi merupakan operasi matematika yang menggabungkan dua fungsi menjadi satu fungsi baru. Fungsi komposisi ini memungkinkan kita untuk mendefinisikan fungsi baru dengan menggunakan hasil dari fungsi lain sebagai input.
Definisi Fungsi Komposisi, Contoh soal fungsi relasi
Fungsi komposisi terjadi ketika output dari satu fungsi digunakan sebagai input untuk fungsi lain. Secara formal, jika kita memiliki dua fungsi, f(x) dan g(x), maka fungsi komposisi f o g (dibaca “f komposisi g”) didefinisikan sebagai:
(f o g)(x) = f(g(x))
Artinya, kita pertama-tama menghitung nilai g(x) dan kemudian menggunakan hasil tersebut sebagai input untuk fungsi f(x).
Contoh Soal Fungsi Komposisi
Misalkan kita memiliki dua fungsi:
- f(x) = x² + 1
- g(x) = 2x – 3
Tentukan (f o g)(x) dan (g o f)(x).
Untuk menentukan (f o g)(x), kita substitusikan g(x) ke dalam fungsi f(x):
(f o g)(x) = f(g(x)) = f(2x – 3) = (2x – 3)² + 1 = 4x² – 12x + 10
Untuk menentukan (g o f)(x), kita substitusikan f(x) ke dalam fungsi g(x):
(g o f)(x) = g(f(x)) = g(x² + 1) = 2(x² + 1) – 3 = 2x² – 1
Diagram Panah Fungsi Komposisi
Diagram panah dapat membantu kita memahami fungsi komposisi dengan lebih jelas. Misalkan kita memiliki dua fungsi f dan g yang didefinisikan sebagai berikut:
- f: A → B, dengan A = 1, 2, 3 dan B = a, b, c
- g: B → C, dengan B = a, b, c dan C = x, y, z
Fungsi komposisi f o g didefinisikan sebagai:
- f o g: A → C
Diagram panah untuk fungsi komposisi f o g akan menunjukkan bagaimana input dari A dipetakan ke output di C melalui fungsi g dan kemudian f. Misalnya, jika f(1) = a dan g(a) = x, maka (f o g)(1) = x.
Diagram panah tersebut akan menunjukkan bahwa untuk setiap input di A, terdapat jalur yang jelas menuju output di C melalui fungsi g dan kemudian f.
Soal-soal Relasi dan Fungsi
Relasi dan fungsi merupakan konsep dasar dalam matematika yang penting untuk dipahami. Relasi menjelaskan hubungan antara dua himpunan, sedangkan fungsi merupakan jenis relasi khusus yang menghubungkan setiap elemen pada himpunan pertama dengan tepat satu elemen pada himpunan kedua. Untuk menguji pemahamanmu tentang relasi dan fungsi, berikut adalah beberapa soal latihan dengan tingkat kesulitan yang bervariasi.
Soal Latihan Relasi dan Fungsi
Soal-soal berikut dirancang untuk menguji pemahamanmu tentang konsep relasi dan fungsi. Cobalah untuk menyelesaikan soal-soal ini secara mandiri sebelum melihat kunci jawaban dan pembahasannya.
| Soal | Jawaban | Pembahasan |
|---|---|---|
| Diketahui himpunan A = 1, 2, 3 dan B = a, b, c. Tentukan banyaknya relasi yang mungkin dari A ke B. | 8 | Setiap elemen di himpunan A dapat dihubungkan dengan 3 elemen di himpunan B. Karena terdapat 3 elemen di himpunan A, maka banyaknya relasi yang mungkin adalah 3 x 3 x 3 = 27. |
| Diketahui relasi R = (1, 2), (2, 3), (3, 1) pada himpunan 1, 2, 3. Tentukan apakah relasi R merupakan fungsi. | Ya | Relasi R merupakan fungsi karena setiap elemen di domain (himpunan pertama) dihubungkan dengan tepat satu elemen di kodomain (himpunan kedua). |
| Diketahui fungsi f(x) = 2x + 1. Tentukan nilai f(3). | 7 | Untuk menentukan nilai f(3), kita substitusikan x = 3 ke dalam fungsi f(x). Maka f(3) = 2(3) + 1 = 6 + 1 = 7. |
| Diketahui fungsi f(x) = x^2 + 2x – 3. Tentukan domain dan range dari fungsi f(x). | Domain: Semua bilangan real. Range: y ≥ -4. | Domain fungsi f(x) adalah semua bilangan real karena tidak ada batasan untuk nilai x yang dapat dimasukkan ke dalam fungsi. Range fungsi f(x) dapat ditentukan dengan mencari nilai minimum fungsi. Nilai minimum fungsi f(x) adalah -4 yang terjadi ketika x = -1. |
| Diketahui fungsi f(x) = 3x – 2 dan g(x) = x^2 + 1. Tentukan nilai (f o g)(2). | 11 | (f o g)(2) berarti kita harus menghitung nilai g(2) terlebih dahulu, kemudian hasil g(2) tersebut disubstitusikan ke dalam fungsi f(x). g(2) = 2^2 + 1 = 5. Selanjutnya, f(5) = 3(5) – 2 = 15 – 2 = 13. |
Terakhir
Memahami relasi dan fungsi tidak hanya penting dalam matematika, tetapi juga dalam berbagai bidang seperti ekonomi, fisika, dan teknologi. Dengan contoh soal fungsi relasi, kita dapat belajar bagaimana konsep ini digunakan untuk menganalisis dan memecahkan masalah di dunia nyata.




