Contoh soal garis singgung persekutuan dalam dan luar – Pernahkah kamu memperhatikan bagaimana dua roda sepeda dapat bersinggungan tanpa saling bertabrakan? Atau bagaimana dua lingkaran pada sebuah peta dapat memiliki titik singgung yang unik? Itulah contoh nyata dari konsep garis singgung persekutuan dalam dan luar. Dalam matematika, konsep ini mengkaji hubungan antara dua lingkaran yang memiliki titik singgung bersama. Kita akan menjelajahi berbagai aspek menarik dari garis singgung persekutuan, mulai dari definisi hingga penerapannya dalam kehidupan sehari-hari.
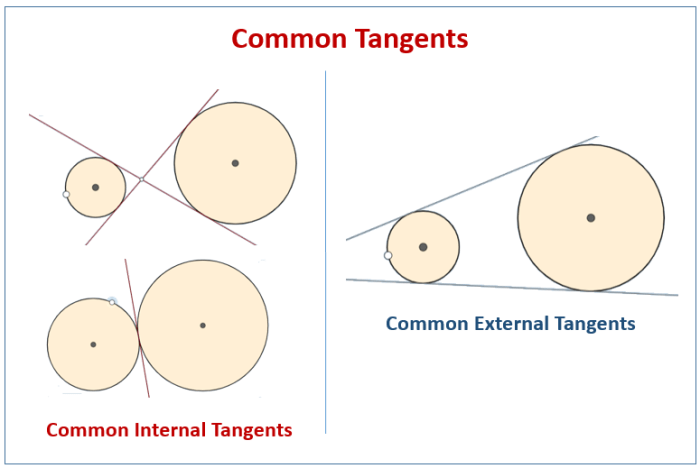
Garis singgung persekutuan adalah garis lurus yang menyinggung dua lingkaran sekaligus. Terdapat dua jenis garis singgung persekutuan, yaitu garis singgung persekutuan dalam dan garis singgung persekutuan luar. Garis singgung persekutuan dalam adalah garis yang berada di antara kedua lingkaran, sedangkan garis singgung persekutuan luar adalah garis yang berada di luar kedua lingkaran.
Pengertian Garis Singgung Persekutuan
Garis singgung persekutuan adalah garis lurus yang menyinggung dua lingkaran sekaligus. Garis singgung persekutuan ini dibedakan menjadi dua jenis, yaitu garis singgung persekutuan dalam dan garis singgung persekutuan luar. Perbedaannya terletak pada posisi garis singgung terhadap kedua lingkaran.
Contoh soal garis singgung persekutuan dalam dan luar bisa kita temukan di buku-buku pelajaran matematika. Nah, kalau kamu lagi belajar tentang investasi dan ingin menghitung kelayakan proyek, kamu bisa cek contoh soal payback period, NPV, dan IRR di sini.
Dengan mempelajari contoh-contoh soal, kamu bisa memahami konsep dan rumus yang digunakan untuk menghitung garis singgung persekutuan dalam dan luar maupun untuk menghitung kelayakan investasi.
Pengertian Garis Singgung Persekutuan Dalam dan Luar
Garis singgung persekutuan dalam adalah garis yang menyinggung kedua lingkaran pada sisi yang sama. Garis ini berada di antara kedua lingkaran. Sementara itu, garis singgung persekutuan luar adalah garis yang menyinggung kedua lingkaran pada sisi yang berbeda. Garis ini berada di luar kedua lingkaran.
Ilustrasi Garis Singgung Persekutuan Dalam dan Luar
Untuk memahami perbedaan kedua jenis garis singgung persekutuan ini, perhatikan ilustrasi berikut:
Bayangkan dua lingkaran dengan pusat A dan B. Garis singgung persekutuan dalam akan melewati titik singgung pada kedua lingkaran yang berada di antara kedua pusat lingkaran. Sementara itu, garis singgung persekutuan luar akan melewati titik singgung pada kedua lingkaran yang berada di luar kedua pusat lingkaran.
Ilustrasi ini menunjukkan bahwa garis singgung persekutuan dalam dan luar memiliki perbedaan yang signifikan dalam posisi dan letaknya terhadap kedua lingkaran.
Perbedaan Ciri-Ciri Garis Singgung Persekutuan Dalam dan Luar
Berikut tabel yang membandingkan ciri-ciri garis singgung persekutuan dalam dan luar:
| Ciri-ciri | Garis Singgung Persekutuan Dalam | Garis Singgung Persekutuan Luar |
|---|---|---|
| Posisi terhadap lingkaran | Menyinggung kedua lingkaran pada sisi yang sama | Menyinggung kedua lingkaran pada sisi yang berbeda |
| Letak terhadap pusat lingkaran | Berada di antara kedua pusat lingkaran | Berada di luar kedua pusat lingkaran |
| Jumlah garis singgung | Mempunyai dua garis singgung | Mempunyai dua garis singgung |
Rumus Garis Singgung Persekutuan
Setelah memahami konsep garis singgung persekutuan, kita akan mempelajari rumus yang digunakan untuk menghitung panjang garis singgung persekutuan dalam dan luar. Rumus ini akan membantu kita dalam menyelesaikan berbagai soal yang berkaitan dengan garis singgung persekutuan.
Rumus Garis Singgung Persekutuan Dalam
Rumus untuk menghitung panjang garis singgung persekutuan dalam (GSB) adalah:
GSB = √(d2 – (r1 – r2)2)
Keterangan:
- GSB adalah panjang garis singgung persekutuan dalam.
- d adalah jarak antara pusat kedua lingkaran.
- r1 adalah jari-jari lingkaran pertama.
- r2 adalah jari-jari lingkaran kedua.
Rumus Garis Singgung Persekutuan Luar
Rumus untuk menghitung panjang garis singgung persekutuan luar (GSL) adalah:
GSL = √(d2 – (r1 + r2)2)
Keterangan:
- GSL adalah panjang garis singgung persekutuan luar.
- d adalah jarak antara pusat kedua lingkaran.
- r1 adalah jari-jari lingkaran pertama.
- r2 adalah jari-jari lingkaran kedua.
Penerapan Garis Singgung Persekutuan dalam Kehidupan Sehari-hari: Contoh Soal Garis Singgung Persekutuan Dalam Dan Luar
Konsep garis singgung persekutuan, baik dalam maupun luar, ternyata memiliki aplikasi yang menarik dalam kehidupan sehari-hari. Meskipun mungkin tidak terlihat secara langsung, konsep ini berperan penting dalam berbagai aspek, mulai dari desain arsitektur hingga pengaturan tata letak dalam ruang.
Contoh Penerapan Garis Singgung Persekutuan dalam, Contoh soal garis singgung persekutuan dalam dan luar
Salah satu contoh penerapan garis singgung persekutuan dalam adalah dalam desain taman bermain. Bayangkan sebuah taman bermain dengan dua buah ayunan yang memiliki titik tumpu yang berbeda. Untuk memastikan kedua ayunan dapat bergerak dengan aman tanpa saling bertabrakan, jarak minimum antara kedua titik tumpu ayunan harus dipertimbangkan. Jarak minimum ini dapat dihitung menggunakan konsep garis singgung persekutuan dalam, dimana garis singgung persekutuan dalam menghubungkan kedua titik tumpu ayunan dan merupakan jarak minimum yang memungkinkan kedua ayunan bergerak bebas tanpa saling bersinggungan.
- Ilustrasi: Bayangkan dua lingkaran yang mewakili titik tumpu ayunan. Garis singgung persekutuan dalam akan menghubungkan kedua lingkaran tersebut dan akan menjadi jarak minimum yang aman agar kedua ayunan dapat bergerak bebas tanpa bertabrakan.
Contoh Penerapan Garis Singgung Persekutuan Luar
Konsep garis singgung persekutuan luar juga dapat diaplikasikan dalam berbagai situasi. Misalnya, dalam desain jembatan, garis singgung persekutuan luar dapat digunakan untuk menentukan jarak minimum antara dua pilar jembatan yang berdekatan. Jarak ini penting untuk memastikan bahwa jembatan dapat menahan beban dan tidak runtuh akibat tekanan yang berlebihan.
- Ilustrasi: Bayangkan dua lingkaran yang mewakili pilar jembatan. Garis singgung persekutuan luar akan menghubungkan kedua lingkaran tersebut dan akan menjadi jarak minimum yang aman agar jembatan dapat menahan beban tanpa runtuh.
Ringkasan Penutup
Memahami konsep garis singgung persekutuan dalam dan luar tidak hanya penting dalam pelajaran matematika, tetapi juga dalam berbagai bidang lainnya. Dari desain arsitektur hingga penempatan satelit, konsep ini berperan penting dalam menciptakan solusi yang efektif dan efisien. Dengan memahami konsep ini, kita dapat lebih memahami dunia di sekitar kita dan menemukan solusi inovatif untuk berbagai permasalahan.





