Pernahkah Anda bertanya-tanya bagaimana planet-planet di tata surya kita bergerak dengan begitu teratur? Rahasia di balik gerakan planet ini terungkap melalui Hukum Kepler, yang diusulkan oleh astronom Johannes Kepler pada abad ke-17. Hukum ini memberikan penjelasan yang akurat tentang orbit planet dan gerakannya di sekitar Matahari. Dalam artikel ini, kita akan menjelajahi contoh soal hukum Kepler untuk memahami lebih dalam tentang konsep ini.
Hukum Kepler terdiri dari tiga hukum utama yang menjelaskan bentuk orbit planet, kecepatan planet, dan hubungan antara periode orbit dan jarak planet dari Matahari. Dengan memahami ketiga hukum ini, kita dapat memahami dengan lebih baik bagaimana tata surya kita berfungsi dan bagaimana planet-planet bergerak di dalamnya.
Pengertian Hukum Kepler
Hukum Kepler tentang gerak planet merupakan serangkaian tiga hukum yang menjelaskan gerakan planet-planet dalam tata surya. Hukum ini ditemukan oleh astronom Jerman, Johannes Kepler, pada awal abad ke-17. Hukum Kepler ini memberikan pemahaman yang lebih baik tentang pergerakan planet dibandingkan dengan teori geosentris yang mendominasi pemikiran ilmiah pada masa itu.
Hukum Kepler I: Hukum Orbit Elips
Hukum Kepler I menyatakan bahwa orbit planet mengelilingi matahari berbentuk elips, dengan matahari berada di salah satu fokusnya.
- Hukum ini menjelaskan bahwa orbit planet tidak berbentuk lingkaran sempurna seperti yang diyakini sebelumnya, melainkan berbentuk elips, yang menyerupai lingkaran yang sedikit tertekan.
- Salah satu fokus elips adalah titik yang tidak berada di pusat elips, dan matahari terletak di salah satu fokus ini. Hal ini berarti bahwa jarak antara planet dan matahari tidak selalu sama, tetapi bervariasi sepanjang orbitnya.
Hukum Kepler II: Hukum Luas
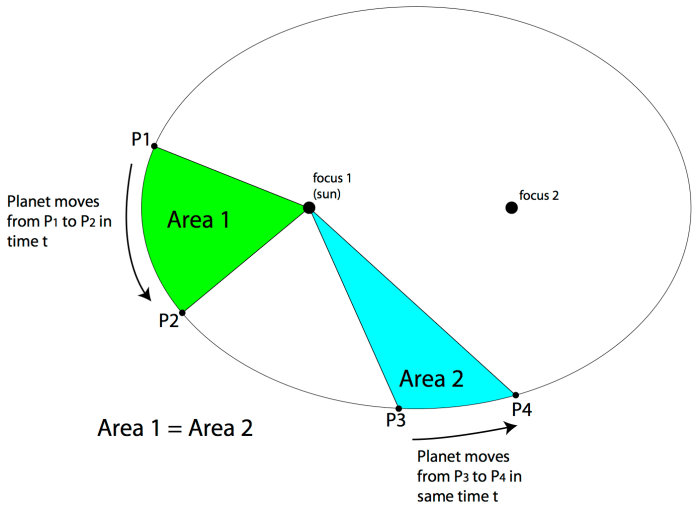
Hukum Kepler II menyatakan bahwa garis yang menghubungkan planet dengan matahari menyapu luas yang sama dalam waktu yang sama.
- Hukum ini menjelaskan bahwa planet bergerak lebih cepat ketika lebih dekat ke matahari dan lebih lambat ketika lebih jauh dari matahari.
- Misalnya, ketika planet berada di titik terdekatnya dengan matahari (disebut perihelion), kecepatannya lebih tinggi dibandingkan ketika berada di titik terjauhnya (disebut aphelion).
- Hal ini dapat diilustrasikan dengan bayangkan sebuah garis yang menghubungkan planet dengan matahari. Garis ini akan menyapu luas yang sama dalam interval waktu yang sama, meskipun kecepatan planet bervariasi.
Hukum Kepler III: Hukum Perioda
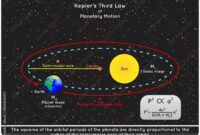
Hukum Kepler III menyatakan bahwa kuadrat periode orbit planet sebanding dengan pangkat tiga dari sumbu semi-mayor orbitnya.
- Hukum ini menjelaskan hubungan antara periode orbit planet (waktu yang dibutuhkan planet untuk menyelesaikan satu putaran mengelilingi matahari) dan ukuran orbitnya.
- Sumbu semi-mayor adalah jarak rata-rata antara planet dan matahari. Semakin besar sumbu semi-mayor, semakin lama periode orbit planet.
- Sebagai contoh, Mars memiliki periode orbit yang lebih lama daripada Bumi karena Mars memiliki sumbu semi-mayor yang lebih besar.
Perbedaan Hukum Kepler dan Hukum Gravitasi Newton
Hukum Kepler menjelaskan bagaimana planet bergerak, tetapi tidak menjelaskan mengapa planet bergerak seperti itu. Hukum gravitasi Newton, yang ditemukan sekitar 60 tahun setelah hukum Kepler, menjelaskan gaya tarik-menarik antara benda-benda bermassa, termasuk matahari dan planet.
- Hukum Kepler merupakan deskripsi empiris tentang gerakan planet, yang didasarkan pada pengamatan dan data.
- Hukum gravitasi Newton, di sisi lain, merupakan hukum fisika yang menjelaskan gaya yang menyebabkan gerakan planet.
- Hukum Kepler dapat dianggap sebagai konsekuensi dari hukum gravitasi Newton.
Hukum Kepler II
Hukum Kepler II, yang juga dikenal sebagai Hukum Luas, menjelaskan hubungan antara kecepatan planet dan jaraknya dari matahari. Hukum ini menyatakan bahwa garis yang menghubungkan planet dengan matahari menyapu luas yang sama dalam waktu yang sama. Artinya, planet bergerak lebih cepat ketika lebih dekat ke matahari dan lebih lambat ketika lebih jauh dari matahari.
Hubungan Kecepatan dan Jarak
Hubungan antara kecepatan planet dan jaraknya dari matahari berdasarkan Hukum Kepler II dapat dijelaskan sebagai berikut:
- Saat planet berada di titik terdekatnya dengan matahari (perihelion), kecepatannya akan lebih tinggi karena garis yang menghubungkan planet dengan matahari menyapu luas yang sama dalam waktu yang lebih singkat.
- Sebaliknya, saat planet berada di titik terjauhnya dari matahari (aphelion), kecepatannya akan lebih rendah karena garis yang menghubungkan planet dengan matahari menyapu luas yang sama dalam waktu yang lebih lama.
Diagram Hubungan Luas dan Waktu
Diagram berikut menunjukkan hubungan antara luas dan waktu berdasarkan Hukum Kepler II:
[Gambar diagram yang menunjukkan hubungan antara luas dan waktu berdasarkan Hukum Kepler II]
Dalam diagram ini, luas yang disapu oleh garis yang menghubungkan planet dengan matahari dalam waktu yang sama (T1, T2, dan T3) adalah sama, meskipun jarak planet dari matahari berbeda. Ini menunjukkan bahwa kecepatan planet tidak konstan, melainkan berubah seiring perubahan jaraknya dari matahari.
Contoh Soal
Sebuah planet bergerak dalam orbit elips mengelilingi matahari. Planet ini berada di perihelion dengan jarak 100 juta km dari matahari dan kecepatannya 40 km/s. Jika luas yang disapu oleh garis yang menghubungkan planet dengan matahari dalam waktu 10 hari adalah 100 juta km2, berapakah kecepatan planet ketika berada di aphelion dengan jarak 200 juta km dari matahari?
Penyelesaian:
Luas yang disapu oleh garis yang menghubungkan planet dengan matahari dalam waktu 10 hari adalah 100 juta km2. Berdasarkan Hukum Kepler II, luas yang disapu dalam waktu yang sama selalu sama.
Ketika planet berada di aphelion, luas yang disapu dalam waktu 10 hari juga 100 juta km2. Namun, jarak planet dari matahari menjadi 200 juta km. Karena luasnya sama, maka kecepatan planet di aphelion akan lebih rendah dibandingkan dengan kecepatannya di perihelion.
Untuk menghitung kecepatan planet di aphelion, kita dapat menggunakan rumus:
vaphelion = (rperihelion / raphelion) * vperihelion
Dimana:
- vaphelion adalah kecepatan planet di aphelion
- rperihelion adalah jarak planet dari matahari di perihelion
- raphelion adalah jarak planet dari matahari di aphelion
- vperihelion adalah kecepatan planet di perihelion
Dengan memasukkan nilai yang diketahui, kita mendapatkan:
vaphelion = (100 juta km / 200 juta km) * 40 km/s = 20 km/s
Jadi, kecepatan planet ketika berada di aphelion adalah 20 km/s.
Hukum Kepler III
Hukum Kepler III, juga dikenal sebagai Hukum Periode, menjelaskan hubungan antara periode orbit suatu planet dan jarak rata-rata planet tersebut dari matahari. Hukum ini menyatakan bahwa kuadrat periode orbit suatu planet sebanding dengan pangkat tiga jarak rata-rata planet tersebut dari matahari.
Hubungan Periode Orbit dan Jarak Rata-rata, Contoh soal hukum kepler
Hukum Kepler III menyatakan bahwa kuadrat periode orbit suatu planet sebanding dengan pangkat tiga jarak rata-rata planet tersebut dari matahari. Artinya, semakin jauh suatu planet dari matahari, semakin lama waktu yang dibutuhkan untuk menyelesaikan satu orbit.
Rumus matematis untuk Hukum Kepler III adalah:
T2 = k * a3
di mana:
* T adalah periode orbit (dalam tahun)
* a adalah jarak rata-rata planet dari matahari (dalam satuan astronomi, AU)
* k adalah konstanta proporsionalitas, yang sama untuk semua planet dalam tata surya
Contoh Soal
Misalnya, jika kita ingin menghitung periode orbit Mars, kita dapat menggunakan Hukum Kepler III. Jarak rata-rata Mars dari matahari adalah 1,52 AU. Dengan menggunakan rumus di atas, kita dapat menghitung periode orbit Mars sebagai berikut:
T2 = k * a3
T2 = 1 * (1,52)3
T2 = 3,51
T = √3,51 = 1,87 tahun
Jadi, periode orbit Mars adalah 1,87 tahun.
Periode Orbit dan Jarak Rata-rata Planet
Berikut adalah tabel yang menunjukkan periode orbit dan jarak rata-rata planet dari matahari untuk beberapa planet di tata surya:
| Planet | Jarak Rata-rata dari Matahari (AU) | Periode Orbit (Tahun) |
|---|---|---|
| Merkurius | 0,39 | 0,24 |
| Venus | 0,72 | 0,62 |
| Bumi | 1,00 | 1,00 |
| Mars | 1,52 | 1,88 |
| Jupiter | 5,20 | 11,86 |
| Saturnus | 9,54 | 29,46 |
| Uranus | 19,22 | 84,01 |
| Neptunus | 30,06 | 164,79 |
Seperti yang dapat kita lihat dari tabel, semakin jauh suatu planet dari matahari, semakin lama waktu yang dibutuhkan untuk menyelesaikan satu orbit.
Penerapan Hukum Kepler
Hukum Kepler, yang merumuskan gerakan planet mengelilingi matahari, bukan hanya sekadar teori abstrak. Hukum ini memiliki aplikasi praktis yang luas dalam berbagai bidang, terutama dalam memahami dan memprediksi gerakan benda langit.
Contoh soal hukum Kepler bisa jadi agak rumit, ya. Tapi, tenang aja! Kamu bisa latihan dulu dengan contoh soal Gerak Lurus Beraturan (GLB) contoh soal glb dan jawabannya untuk memahami konsep dasar pergerakan. Setelah itu, kamu akan lebih mudah memahami hukum Kepler yang berhubungan dengan pergerakan planet-planet di tata surya.
Menentukan Posisi Planet di Masa Depan
Hukum Kepler memungkinkan kita untuk menghitung posisi planet di masa depan dengan akurasi yang tinggi. Dengan mengetahui periode orbit planet, bentuk orbitnya (elips), dan posisi awal planet, kita dapat memprediksi posisi planet tersebut pada waktu tertentu di masa depan.
Sebagai contoh, dengan menggunakan Hukum Kepler, para astronom dapat memprediksi kapan planet tertentu akan berada pada posisi terdekat atau terjauh dari matahari. Informasi ini penting untuk perencanaan misi ruang angkasa, seperti menentukan waktu terbaik untuk meluncurkan wahana antariksa menuju planet tertentu.
Penerapan dalam Astronomi dan Astrofisika
Hukum Kepler memiliki aplikasi penting dalam berbagai bidang astronomi dan astrofisika, termasuk:
- Penentuan Massa Bintang: Dengan mengamati gerakan planet mengelilingi bintang, kita dapat menentukan massa bintang tersebut menggunakan Hukum Kepler.
- Pencarian Planet Ekstrasurya: Hukum Kepler digunakan untuk mendeteksi dan mempelajari planet di luar sistem tata surya kita. Metode transit, yang mengandalkan Hukum Kepler, digunakan untuk mendeteksi penurunan cahaya bintang saat planet melintas di depannya.
- Pemahaman Evolusi Bintang: Hukum Kepler membantu kita memahami bagaimana bintang berevolusi. Dengan mengamati gerakan bintang ganda, kita dapat menentukan massa dan evolusi bintang tersebut.
- Penentuan Jarak Bintang: Hukum Kepler, bersama dengan hukum gravitasi Newton, digunakan untuk menentukan jarak bintang dengan metode paralaks.
“Hukum Kepler adalah tonggak penting dalam sejarah astronomi. Hukum ini mengubah cara kita memahami alam semesta dan membuka jalan bagi pemahaman yang lebih mendalam tentang gerakan planet dan bintang.” – Sir Isaac Newton
Pengembangan Hukum Kepler
Hukum Kepler, yang menjelaskan pergerakan planet-planet dalam tata surya, merupakan hasil dari pengamatan dan analisis yang cermat selama bertahun-tahun. Johannes Kepler, seorang astronom Jerman, mengembangkan hukum-hukum ini setelah mempelajari data pengamatan yang dikumpulkan oleh Tycho Brahe, astronom Denmark yang terkenal.
Pengamatan dan Analisis Data
Kepler memulai pekerjaannya dengan menganalisis data pengamatan yang telah dikumpulkan oleh Tycho Brahe selama bertahun-tahun. Data ini sangat akurat dan terperinci, mencakup posisi Mars selama periode waktu yang lama. Kepler menyadari bahwa orbit Mars bukanlah lingkaran sempurna seperti yang diyakini oleh para astronom sebelumnya, melainkan elips.
Dengan menggunakan data ini, Kepler menemukan bahwa orbit Mars bukanlah lingkaran sempurna seperti yang diyakini oleh para astronom sebelumnya, melainkan elips. Dia juga menemukan bahwa kecepatan planet tidak konstan saat bergerak mengelilingi matahari, tetapi lebih cepat saat planet berada lebih dekat ke matahari dan lebih lambat saat berada lebih jauh.
Eksperimen Verifikasi
Hukum Kepler dapat diuji dengan menggunakan berbagai eksperimen. Salah satu eksperimen yang sederhana adalah dengan menggunakan model planetarium. Model ini dapat menunjukkan bagaimana planet-planet bergerak mengelilingi matahari dan bagaimana kecepatan mereka berubah.
- Eksperimen lain yang lebih kompleks melibatkan penggunaan teleskop untuk mengamati posisi planet-planet dan kemudian membandingkan hasil pengamatan dengan prediksi yang dibuat berdasarkan Hukum Kepler.
- Eksperimen-eksperimen ini telah secara konsisten mengonfirmasi keakuratan Hukum Kepler.
Pengaruh Penemuan Ilmiah Baru
Penemuan-penemuan ilmiah baru telah memberikan pemahaman yang lebih mendalam tentang Hukum Kepler. Misalnya, penemuan gravitasi oleh Isaac Newton menjelaskan mengapa planet-planet bergerak dalam orbit elips dan mengapa kecepatan mereka berubah.
Teori relativitas umum Einstein juga telah memberikan pemahaman yang lebih akurat tentang gravitasi, yang telah memungkinkan para ilmuwan untuk mengukur dengan lebih tepat orbit planet-planet dan untuk memprediksi pergerakan mereka dengan lebih akurat.
Keterbatasan Hukum Kepler: Contoh Soal Hukum Kepler
Hukum Kepler, yang dirumuskan oleh Johannes Kepler pada awal abad ke-17, memberikan deskripsi yang akurat tentang gerak planet dalam sistem tata surya kita. Hukum-hukum ini telah menjadi dasar pemahaman kita tentang mekanika langit dan telah memungkinkan kita untuk memprediksi posisi planet di masa depan. Namun, Hukum Kepler memiliki beberapa keterbatasan, dan tidak dapat menjelaskan semua aspek gerak planet.
Keterbatasan Hukum Kepler
Hukum Kepler hanya berlaku untuk gerak planet dalam sistem tata surya kita, dan tidak dapat menjelaskan gerak benda langit lainnya, seperti komet atau asteroid. Hukum Kepler juga mengasumsikan bahwa gaya gravitasi hanya bekerja antara matahari dan planet, dan tidak memperhitungkan pengaruh gravitasi dari planet lain. Selain itu, Hukum Kepler mengasumsikan bahwa planet bergerak dalam orbit elips yang sempurna, padahal sebenarnya orbit planet sedikit menyimpang dari bentuk elips sempurna karena pengaruh gravitasi dari planet lain.
Contoh Kasus di mana Hukum Kepler Tidak Berlaku
Contoh kasus di mana Hukum Kepler tidak berlaku adalah gerak komet. Komet memiliki orbit yang sangat eksentrik, yang berarti bahwa orbit mereka sangat memanjang dan tidak berbentuk elips sempurna. Komet juga dipengaruhi oleh gaya gravitasi dari matahari dan planet lain, sehingga gerakan mereka tidak dapat dijelaskan secara akurat oleh Hukum Kepler.
Modifikasi Hukum Kepler
Untuk mengatasi keterbatasan Hukum Kepler, para ilmuwan telah mengembangkan teori gravitasi Newton. Teori gravitasi Newton memperhitungkan pengaruh gravitasi dari semua benda langit, dan dapat menjelaskan gerak benda langit yang lebih kompleks, seperti komet dan asteroid. Teori gravitasi Newton juga memperhitungkan bahwa orbit planet tidak berbentuk elips sempurna, tetapi sedikit menyimpang dari bentuk elips sempurna karena pengaruh gravitasi dari planet lain.
Ringkasan Terakhir
Mempelajari Hukum Kepler tidak hanya memberikan pemahaman tentang gerakan planet, tetapi juga membuka jalan bagi pemahaman yang lebih dalam tentang hukum gravitasi Newton. Dengan memahami hukum-hukum ini, kita dapat menelusuri sejarah perkembangan ilmu pengetahuan dan melihat bagaimana para ilmuwan berusaha untuk mengungkap rahasia alam semesta.