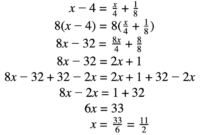Contoh soal kalkulus 1 – Kalkulus 1 merupakan cabang ilmu matematika yang mempelajari konsep limit, turunan, integral, dan deret tak hingga. Materi ini menjadi dasar untuk memahami berbagai konsep matematika tingkat lanjut, seperti kalkulus multivariabel, persamaan diferensial, dan analisis numerik.
Dalam artikel ini, kita akan membahas beberapa contoh soal Kalkulus 1 yang mencakup berbagai topik, mulai dari limit dan turunan hingga integral dan deret tak hingga. Dengan memahami konsep dan rumus yang digunakan dalam penyelesaian setiap soal, Anda dapat meningkatkan pemahaman dan kemampuan dalam menyelesaikan soal Kalkulus 1.
Konsep Dasar Kalkulus 1: Contoh Soal Kalkulus 1
Kalkulus 1 merupakan dasar dari matematika tingkat lanjut dan memiliki aplikasi luas dalam berbagai bidang, seperti fisika, teknik, ekonomi, dan ilmu komputer. Konsep-konsep utama dalam Kalkulus 1 meliputi limit, turunan, dan integral. Dalam artikel ini, kita akan membahas konsep limit yang merupakan pondasi dari kalkulus.
Konsep Limit dalam Kalkulus 1
Limit merupakan konsep yang menggambarkan perilaku suatu fungsi ketika variabel input mendekati suatu nilai tertentu. Konsep limit memungkinkan kita untuk menganalisis fungsi pada titik-titik yang tidak terdefinisi atau pada titik-titik di mana fungsi tersebut tidak kontinu. Dalam konteks limit, kita tidak peduli dengan nilai fungsi pada titik tersebut, tetapi kita tertarik pada nilai yang didekati fungsi tersebut saat variabel input mendekati titik tersebut.
Jenis-Jenis Limit
Terdapat beberapa jenis limit dalam Kalkulus 1, yang dibedakan berdasarkan perilaku fungsi saat variabel input mendekati titik tertentu. Berikut adalah tabel yang merangkum jenis-jenis limit dan contohnya:
| Jenis Limit | Definisi | Contoh |
|---|---|---|
| Limit Sisi Satu | Limit yang dihitung dari satu sisi titik tertentu, baik dari kiri atau kanan. | Limit fungsi f(x) = 1/x ketika x mendekati 0 dari kanan: lim x→0+ 1/x = ∞ |
| Limit Dua Sisi | Limit yang dihitung dari kedua sisi titik tertentu, baik dari kiri maupun kanan. | Limit fungsi f(x) = x^2 ketika x mendekati 2: lim x→2 x^2 = 4 |
| Limit Tak Hingga | Limit yang dihitung ketika variabel input mendekati tak hingga. | Limit fungsi f(x) = 1/x ketika x mendekati tak hingga: lim x→∞ 1/x = 0 |
| Limit Tak Terdefinisi | Limit yang tidak memiliki nilai tertentu, biasanya terjadi ketika fungsi memiliki bentuk tak tentu. | Limit fungsi f(x) = 1/x ketika x mendekati 0: lim x→0 1/x = tak terdefinisi |
Contoh Soal Limit dan Penyelesaiannya, Contoh soal kalkulus 1
Misalkan kita ingin mencari limit fungsi f(x) = (x^2 – 4) / (x – 2) ketika x mendekati 2.
Langkah-langkah penyelesaiannya:
- Substitusikan nilai x = 2 ke dalam fungsi f(x): (2^2 – 4) / (2 – 2) = 0/0. Ini merupakan bentuk tak tentu.
- Faktorkan fungsi f(x): (x^2 – 4) / (x – 2) = (x + 2)(x – 2) / (x – 2)
- Sederhanakan fungsi f(x) dengan menghilangkan faktor (x – 2): f(x) = x + 2
- Substitusikan kembali nilai x = 2 ke dalam fungsi f(x) yang telah disederhanakan: 2 + 2 = 4
- Jadi, limit fungsi f(x) = (x^2 – 4) / (x – 2) ketika x mendekati 2 adalah 4: lim x→2 (x^2 – 4) / (x – 2) = 4
Aplikasi Turunan Fungsi
Turunan fungsi merupakan konsep penting dalam kalkulus yang memiliki berbagai aplikasi dalam matematika, fisika, ekonomi, dan bidang lainnya. Salah satu aplikasi turunan fungsi yang penting adalah untuk menentukan titik stasioner suatu fungsi.
Titik Stasioner
Titik stasioner suatu fungsi adalah titik di mana turunan pertama fungsi tersebut sama dengan nol atau tidak terdefinisi. Pada titik stasioner, fungsi mencapai nilai maksimum, minimum, atau titik belok.
Turunan pertama fungsi f(x) sama dengan nol, atau tidak terdefinisi, pada titik stasioner.
Jenis-Jenis Titik Stasioner
Titik stasioner dapat diklasifikasikan menjadi beberapa jenis berdasarkan nilai turunan kedua fungsi pada titik tersebut.
- Titik Maksimum: Pada titik maksimum, turunan pertama fungsi sama dengan nol dan turunan kedua fungsi bernilai negatif. Titik ini menunjukkan bahwa fungsi mencapai nilai maksimum lokal di titik tersebut.
- Titik Minimum: Pada titik minimum, turunan pertama fungsi sama dengan nol dan turunan kedua fungsi bernilai positif. Titik ini menunjukkan bahwa fungsi mencapai nilai minimum lokal di titik tersebut.
- Titik Belok: Pada titik belok, turunan pertama fungsi sama dengan nol dan turunan kedua fungsi sama dengan nol atau tidak terdefinisi. Titik ini menunjukkan bahwa fungsi berubah dari cekung ke cembung atau sebaliknya.
Contoh Penerapan Turunan Fungsi
Misalkan kita ingin menentukan nilai maksimum dan minimum fungsi f(x) = x^3 – 3x^2 + 2. Untuk menentukan titik stasioner, kita perlu mencari turunan pertama fungsi tersebut.
f'(x) = 3x^2 – 6x
Kemudian, kita cari nilai x yang membuat f'(x) = 0.
3x^2 – 6x = 0
3x(x – 2) = 0
x = 0 atau x = 2
Jadi, titik stasioner fungsi f(x) adalah x = 0 dan x = 2. Untuk menentukan jenis titik stasioner, kita perlu mencari turunan kedua fungsi f(x).
f”(x) = 6x – 6
Pada x = 0, f”(0) = -6, sehingga titik x = 0 merupakan titik maksimum. Pada x = 2, f”(2) = 6, sehingga titik x = 2 merupakan titik minimum.
Aplikasi Integral Fungsi
Integral fungsi memiliki aplikasi yang luas dalam berbagai bidang, termasuk fisika, teknik, ekonomi, dan ilmu komputer. Salah satu aplikasi yang paling penting adalah menghitung luas daerah di bawah kurva.
Menghitung Luas Daerah di Bawah Kurva
Integral fungsi dapat digunakan untuk menghitung luas daerah yang dibatasi oleh kurva, sumbu x, dan garis vertikal. Luas daerah ini dihitung dengan mengintegrasikan fungsi dari batas bawah hingga batas atas integrasi.
Misalnya, untuk menghitung luas daerah di bawah kurva fungsi f(x) = x^2 dari x = 0 hingga x = 2, kita dapat menggunakan integral tentu:
Luas = ∫02 x^2 dx
Hasil integrasi akan memberikan nilai luas daerah di bawah kurva.
Contoh soal kalkulus 1 memang seringkali terlihat rumit, tapi sebenarnya banyak konsep yang bisa dipelajari dengan mudah. Salah satu contohnya adalah aplikasi dari deret geometri tak hingga, seperti pada soal cerita tentang bola yang dijatuhkan dari ketinggian tertentu. Ingin tahu bagaimana deret geometri tak hingga bisa diterapkan dalam soal cerita?
Kunjungi contoh soal cerita deret geometri tak hingga untuk mendapatkan gambaran yang lebih jelas. Setelah mempelajari soal cerita tersebut, kamu akan lebih memahami bagaimana konsep deret geometri tak hingga bisa dihubungkan dengan contoh soal kalkulus 1 yang lain.
Jenis-Jenis Integral dan Contohnya
Terdapat beberapa jenis integral yang digunakan dalam kalkulus, masing-masing dengan karakteristik dan aplikasi yang berbeda.
| Jenis Integral | Contoh |
|---|---|
| Integral Tak Tentu | ∫ x^2 dx = (1/3)x^3 + C |
| Integral Tentu | ∫02 x^2 dx = (1/3)x^3 |02 = (8/3) – 0 = 8/3 |
| Integral Ganda | ∫∫R f(x, y) dA |
| Integral Garis | ∫C f(x, y) ds |
Contoh Soal Penerapan Integral Fungsi dalam Menghitung Volume Benda Putar
Misalkan kita ingin menghitung volume benda putar yang dihasilkan dengan memutar daerah yang dibatasi oleh kurva y = x^2, sumbu x, dan garis x = 2 di sekitar sumbu x.
Untuk menghitung volume benda putar, kita dapat menggunakan metode cakram. Metode cakram menghitung volume dengan mengintegrasikan luas penampang melintang benda putar. Dalam kasus ini, penampang melintang adalah lingkaran dengan jari-jari y = x^2.
Volume benda putar dapat dihitung dengan rumus:
Volume = π∫02 (x^2)^2 dx
Hasil integrasi akan memberikan nilai volume benda putar.
Contoh Soal Kalkulus 1

Kalkulus 1 merupakan mata kuliah dasar yang mempelajari konsep-konsep penting dalam matematika, seperti limit, turunan, integral, dan deret tak hingga. Materi ini sangat penting sebagai fondasi untuk memahami konsep-konsep matematika yang lebih kompleks di tingkat lanjut. Artikel ini akan membahas beberapa contoh soal Kalkulus 1 yang mencakup berbagai topik, lengkap dengan solusi dan penjelasannya.
Limit Fungsi
Limit fungsi merupakan konsep dasar dalam kalkulus yang menggambarkan nilai yang didekati oleh fungsi ketika variabel input mendekati suatu nilai tertentu. Konsep limit sangat penting dalam memahami kontinuitas, turunan, dan integral.
- Tentukan limit fungsi f(x) = (x^2 – 4) / (x – 2) ketika x mendekati 2.
Solusi:
Untuk menyelesaikan soal ini, kita dapat menggunakan metode substitusi langsung. Namun, jika kita langsung substitusikan x = 2 ke dalam fungsi, kita akan mendapatkan bentuk tak tentu 0/0. Oleh karena itu, kita perlu menyederhanakan fungsi terlebih dahulu.
f(x) = (x^2 – 4) / (x – 2) = (x + 2)(x – 2) / (x – 2)
Karena x ≠ 2, maka kita dapat menyederhanakan fungsi menjadi:
f(x) = x + 2
Sekarang, kita dapat langsung substitusikan x = 2 ke dalam fungsi yang telah disederhanakan:
lim x→2 f(x) = lim x→2 (x + 2) = 2 + 2 = 4
Jadi, limit fungsi f(x) = (x^2 – 4) / (x – 2) ketika x mendekati 2 adalah 4.
Turunan Fungsi
Turunan fungsi merupakan konsep yang menggambarkan laju perubahan fungsi terhadap perubahan variabel input. Konsep turunan sangat penting dalam menentukan nilai maksimum dan minimum suatu fungsi, serta dalam mempelajari gerak benda.
- Tentukan turunan pertama dari fungsi f(x) = x^3 + 2x^2 – 5x + 1.
Solusi:
Untuk menyelesaikan soal ini, kita dapat menggunakan aturan turunan dasar. Aturan turunan dasar menyatakan bahwa turunan dari x^n adalah nx^(n-1).
f'(x) = 3x^2 + 4x – 5
Jadi, turunan pertama dari fungsi f(x) = x^3 + 2x^2 – 5x + 1 adalah f'(x) = 3x^2 + 4x – 5.
Integral Fungsi
Integral fungsi merupakan konsep yang menggambarkan luas daerah di bawah kurva fungsi. Konsep integral sangat penting dalam menghitung volume, luas permukaan, dan dalam mempelajari gerak benda.
- Tentukan integral tak tentu dari fungsi f(x) = 2x + 1.
Solusi:
Untuk menyelesaikan soal ini, kita dapat menggunakan aturan integral dasar. Aturan integral dasar menyatakan bahwa integral dari x^n adalah (1/(n+1))x^(n+1) + C, dengan C adalah konstanta integrasi.
∫(2x + 1) dx = x^2 + x + C
Jadi, integral tak tentu dari fungsi f(x) = 2x + 1 adalah x^2 + x + C.
Deret Tak Hingga
Deret tak hingga merupakan penjumlahan tak terhingga suku-suku dalam suatu barisan. Konsep deret tak hingga sangat penting dalam mempelajari fungsi, persamaan diferensial, dan dalam pemodelan matematika.
- Tentukan apakah deret tak hingga 1 + 1/2 + 1/4 + 1/8 + … konvergen atau divergen.
Solusi:
Deret ini merupakan deret geometri dengan rasio 1/2. Sebuah deret geometri konvergen jika dan hanya jika nilai absolut dari rasionya kurang dari 1. Dalam kasus ini, |1/2| < 1, sehingga deret ini konvergen.
Jumlah deret geometri konvergen dapat dihitung dengan rumus S = a / (1 – r), dengan a adalah suku pertama dan r adalah rasio. Dalam kasus ini, a = 1 dan r = 1/2, sehingga jumlah deretnya adalah:
S = 1 / (1 – 1/2) = 2
Jadi, deret tak hingga 1 + 1/2 + 1/4 + 1/8 + … konvergen dan jumlahnya adalah 2.
Sumber Belajar Kalkulus 1
Kalkulus 1 merupakan mata kuliah dasar di berbagai bidang ilmu pengetahuan dan teknologi. Materi yang dipelajari meliputi konsep limit, turunan, integral, dan penerapannya dalam memecahkan masalah matematika dan real-world problems. Untuk mempelajari Kalkulus 1 secara efektif, dibutuhkan sumber belajar yang tepat dan komprehensif.
Buku Teks Kalkulus 1
Buku teks Kalkulus 1 yang direkomendasikan umumnya memiliki ciri-ciri berikut:
- Materi yang disajikan secara sistematis dan mudah dipahami.
- Banyak contoh soal dan latihan yang membantu dalam memahami konsep.
- Penyajian yang menarik dan memotivasi.
Beberapa buku teks Kalkulus 1 yang direkomendasikan:
- Calculus: Early Transcendentals oleh James Stewart
- Calculus oleh Ron Larson dan Bruce Edwards
- Calculus oleh George B. Thomas dan Ross L. Finney
- Calculus: A Complete Course oleh Robert A. Adams dan Christopher Essex
Sumber Belajar Online
Selain buku teks, terdapat banyak sumber belajar online yang dapat membantu dalam mempelajari Kalkulus 1.
- Khan Academy: Platform online yang menyediakan materi belajar Kalkulus 1 secara gratis, lengkap dengan video tutorial, latihan soal, dan contoh soal.
- MIT OpenCourseware: Situs web yang menyediakan materi kuliah Kalkulus 1 dari Massachusetts Institute of Technology (MIT) secara gratis, termasuk video kuliah, catatan kuliah, dan soal latihan.
- Coursera: Platform online yang menyediakan berbagai kursus Kalkulus 1 dari berbagai universitas ternama di dunia, baik yang gratis maupun berbayar.
- edX: Platform online yang menyediakan kursus Kalkulus 1 dari berbagai universitas ternama di dunia, baik yang gratis maupun berbayar.
Manfaat Belajar Kalkulus 1 dari Berbagai Sumber
Belajar Kalkulus 1 dari berbagai sumber dapat memberikan manfaat berikut:
- Memahami konsep Kalkulus 1 secara lebih mendalam.
- Memperoleh berbagai sudut pandang dan metode penyelesaian masalah.
- Meningkatkan kemampuan berpikir kritis dan analitis.
- Memperoleh pengalaman belajar yang lebih interaktif dan menyenangkan.
Ringkasan Penutup
Melalui contoh soal Kalkulus 1 yang telah dibahas, kita dapat melihat bahwa memahami konsep dasar dan rumus yang digunakan merupakan kunci dalam menyelesaikan soal. Dengan latihan yang cukup dan strategi yang tepat, Anda dapat menaklukkan tantangan dalam mempelajari Kalkulus 1.