Contoh soal kpk dan fpb dengan pohon faktor – Pernahkah Anda kesulitan mencari Kelipatan Persekutuan Terkecil (KPK) dan Faktor Persekutuan Terbesar (FPB) dari beberapa bilangan? Tenang, Anda tidak sendirian! Banyak orang yang merasa bingung dengan konsep ini. Namun, dengan metode pohon faktor, mencari KPK dan FPB bisa jadi lebih mudah dan menyenangkan. Metode ini memungkinkan Anda untuk memecah bilangan menjadi faktor-faktor prima, sehingga Anda dapat dengan mudah menemukan KPK dan FPB-nya.
Dalam artikel ini, kita akan menjelajahi metode pohon faktor secara mendalam. Anda akan mempelajari langkah-langkahnya, melihat contoh soal, dan bahkan menemukan bagaimana konsep KPK dan FPB diterapkan dalam kehidupan sehari-hari. Siap untuk mengasah kemampuan matematika Anda? Mari kita mulai!
Penerapan KPK dan FPB dalam Kehidupan Sehari-hari
KPK dan FPB bukan hanya konsep matematika yang dipelajari di sekolah. Keduanya memiliki peran penting dalam kehidupan sehari-hari, membantu kita menyelesaikan berbagai masalah dengan lebih efisien. Dalam artikel ini, kita akan membahas beberapa contoh penerapan KPK dan FPB dalam berbagai bidang kehidupan.
Contoh Penerapan KPK
KPK (Kelipatan Persekutuan Terkecil) berguna dalam menentukan waktu kejadian yang bersamaan. Contohnya, jika dua bus berangkat dari terminal yang sama dengan jadwal keberangkatan berbeda, KPK dari waktu keberangkatan kedua bus akan menunjukkan waktu mereka berangkat bersamaan.
- Misalnya, bus A berangkat setiap 30 menit, dan bus B berangkat setiap 45 menit. KPK dari 30 dan 45 adalah 90. Artinya, kedua bus akan berangkat bersamaan setiap 90 menit.
Contoh Penerapan FPB, Contoh soal kpk dan fpb dengan pohon faktor
FPB (Faktor Persekutuan Terbesar) berguna untuk membagi suatu objek menjadi bagian yang sama besar. Contohnya, jika kita memiliki beberapa buah apel dan ingin membaginya secara merata kepada beberapa orang, FPB dari jumlah apel dan jumlah orang akan menunjukkan jumlah apel yang diterima setiap orang.
- Misalnya, kita memiliki 12 buah apel dan ingin membaginya kepada 4 orang. FPB dari 12 dan 4 adalah 4. Artinya, setiap orang akan mendapatkan 3 buah apel.
Penerapan KPK dan FPB di Berbagai Bidang
| Bidang | Contoh Kasus KPK | Contoh Kasus FPB |
|---|---|---|
| Kuliner | Menentukan waktu yang tepat untuk menguleni adonan roti agar kedua jenis roti matang bersamaan | Membagi adonan kue menjadi bagian yang sama besar untuk dibagikan kepada beberapa orang |
| Perdagangan | Menentukan waktu penjualan barang yang sama di beberapa toko agar terjadi kesamaan stok | Membagi barang dagangan menjadi paket yang sama besar untuk dijual dengan harga lebih murah |
| Konstruksi | Menentukan waktu pengerjaan proyek yang sama oleh beberapa tim pekerja agar selesai bersamaan | Membagi bahan bangunan menjadi bagian yang sama besar untuk digunakan oleh beberapa pekerja |
Variasi Metode Pencarian KPK dan FPB
Selain metode pohon faktor, terdapat beberapa metode lain yang dapat digunakan untuk mencari KPK dan FPB dari dua bilangan atau lebih. Metode-metode ini memiliki kelebihan dan kekurangan masing-masing, sehingga penting untuk memahami dan memilih metode yang paling tepat untuk menyelesaikan masalah yang dihadapi.
Metode Faktorisasi Prima
Metode faktorisasi prima melibatkan pemfaktoran setiap bilangan menjadi faktor-faktor primanya. KPK diperoleh dengan mengalikan faktor prima yang sama dan berbeda dengan pangkat tertinggi, sedangkan FPB diperoleh dengan mengalikan faktor prima yang sama dengan pangkat terendah.
Misalnya, untuk mencari KPK dan FPB dari 12 dan 18:
- Faktorisasi prima dari 12 adalah 2 x 2 x 3 (22 x 3)
- Faktorisasi prima dari 18 adalah 2 x 3 x 3 (2 x 32)
KPK dari 12 dan 18 adalah 22 x 32 = 36
Mempelajari contoh soal KPK dan FPB dengan pohon faktor bisa jadi lebih mudah dengan memahami konsep dasar matematika. Misalnya, kita bisa menghubungkan topik ini dengan contoh soal sistem persamaan dan pertidaksamaan linear kelas 10 seperti yang dibahas di situs ini.
Dengan memahami konsep dasar sistem persamaan, kita bisa lebih mudah memahami cara menyelesaikan soal KPK dan FPB dengan pohon faktor, karena keduanya melibatkan penguraian bilangan menjadi faktor-faktor prima.
FPB dari 12 dan 18 adalah 2 x 3 = 6
Metode Pembagian Bersusun
Metode pembagian bersusun melibatkan pembagian bilangan terbesar dengan bilangan terkecil secara berulang hingga diperoleh sisa 0. KPK diperoleh dengan mengalikan semua pembagi dan sisa terakhir, sedangkan FPB diperoleh dengan mengalikan semua pembagi.
Misalnya, untuk mencari KPK dan FPB dari 24 dan 36:
- Bagilah 36 dengan 24, diperoleh sisa 12.
- Bagilah 24 dengan 12, diperoleh sisa 0.
KPK dari 24 dan 36 adalah 24 x 12 = 288
FPB dari 24 dan 36 adalah 24.
Metode Kelipatan Persekutuan
Metode kelipatan persekutuan melibatkan pencarian kelipatan persekutuan dari dua bilangan atau lebih. KPK diperoleh dengan mencari kelipatan persekutuan terkecil, sedangkan FPB diperoleh dengan mencari faktor persekutuan terbesar.
Misalnya, untuk mencari KPK dan FPB dari 8 dan 12:
- Kelipatan persekutuan dari 8 adalah 8, 16, 24, 32, 40, 48, …
- Kelipatan persekutuan dari 12 adalah 12, 24, 36, 48, …
KPK dari 8 dan 12 adalah 24.
Faktor persekutuan dari 8 dan 12 adalah 1, 2, 4.
FPB dari 8 dan 12 adalah 4.
Perbandingan Metode Pencarian KPK dan FPB
| Metode | Kelebihan | Kekurangan |
|---|---|---|
| Pohon Faktor | Mudah dipahami dan diterapkan. | Kurang efisien untuk bilangan besar. |
| Faktorisasi Prima | Efisien untuk bilangan besar. | Membutuhkan kemampuan untuk memfaktorkan bilangan. |
| Pembagian Bersusun | Efisien untuk bilangan besar. | Membutuhkan kemampuan untuk melakukan pembagian bersusun. |
| Kelipatan Persekutuan | Mudah dipahami dan diterapkan. | Kurang efisien untuk bilangan besar. |
Tips dan Trik Mencari KPK dan FPB: Contoh Soal Kpk Dan Fpb Dengan Pohon Faktor
Mencari KPK dan FPB dengan metode pohon faktor memang mudah, tapi ada beberapa tips dan trik yang bisa kamu gunakan untuk mempercepat prosesnya dan menghindari kesalahan. Dengan memahami tips dan trik ini, kamu akan lebih mudah dalam menyelesaikan soal-soal yang berkaitan dengan KPK dan FPB.
Memilih Faktor Prima yang Tepat
Saat membuat pohon faktor, kamu bisa memilih faktor prima yang tepat untuk mempercepat proses pemfaktoran. Misalnya, jika kamu ingin memfaktorkan angka 24, kamu bisa langsung membaginya dengan 2, lalu 2 lagi, dan seterusnya. Namun, jika kamu memilih faktor prima yang lebih besar, seperti 3 atau 4, proses pemfaktoran akan lebih lama.
- Tips: Mulailah dengan faktor prima terkecil, yaitu 2, lalu lanjutkan dengan 3, 5, 7, dan seterusnya.
- Contoh: Misalnya, untuk mencari KPK dari 12 dan 18, kita bisa memfaktorkan kedua angka tersebut dengan faktor prima 2, 3, dan seterusnya.
Memanfaatkan Faktor Persekutuan
Setelah kamu mendapatkan faktor prima dari kedua angka, kamu bisa langsung mencari faktor persekutuannya. Faktor persekutuan adalah faktor prima yang sama yang dimiliki oleh kedua angka tersebut. Faktor persekutuan ini akan digunakan untuk mencari FPB.
- Tips: Perhatikan faktor prima yang sama pada kedua angka, lalu kalikan faktor prima tersebut.
- Contoh: Misalnya, faktor prima dari 12 adalah 2 x 2 x 3, dan faktor prima dari 18 adalah 2 x 3 x 3. Faktor persekutuan dari 12 dan 18 adalah 2 x 3 = 6. Jadi, FPB dari 12 dan 18 adalah 6.
Menggunakan Faktor Kelipatan
Setelah kamu mendapatkan faktor prima dari kedua angka, kamu bisa langsung mencari faktor kelipatannya. Faktor kelipatan adalah faktor prima yang dimiliki oleh kedua angka tersebut, tetapi tidak selalu sama. Faktor kelipatan ini akan digunakan untuk mencari KPK.
- Tips: Perhatikan faktor prima yang dimiliki oleh kedua angka, lalu kalikan semua faktor prima tersebut.
- Contoh: Misalnya, faktor prima dari 12 adalah 2 x 2 x 3, dan faktor prima dari 18 adalah 2 x 3 x 3. Faktor kelipatan dari 12 dan 18 adalah 2 x 2 x 3 x 3 = 36. Jadi, KPK dari 12 dan 18 adalah 36.
Menghindari Kesalahan
Saat mencari KPK dan FPB dengan metode pohon faktor, ada beberapa kesalahan yang sering dilakukan. Berikut adalah beberapa kesalahan yang harus dihindari:
- Kesalahan: Memilih faktor prima yang tidak tepat.
- Kesalahan: Tidak memperhatikan faktor prima yang sama dan berbeda.
- Kesalahan: Salah menghitung faktor prima.
Latihan Soal
Berikut adalah contoh soal yang bisa kamu gunakan untuk berlatih mencari KPK dan FPB dengan metode pohon faktor:
| Soal | Penyelesaian |
|---|---|
| Carilah KPK dan FPB dari 24 dan 36! | Pohon faktor 24: 2 x 2 x 2 x 3 Pohon faktor 36: 2 x 2 x 3 x 3 FPB: 2 x 2 x 3 = 12 KPK: 2 x 2 x 2 x 3 x 3 = 72 |
Penutup
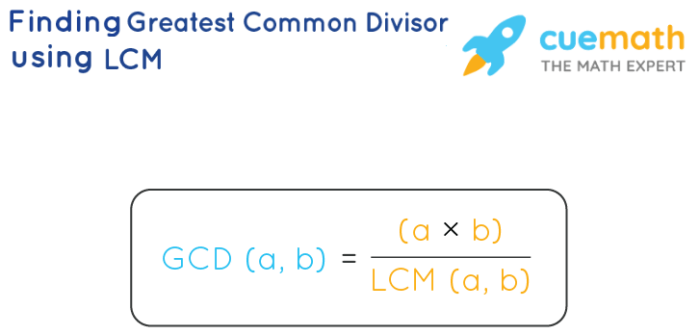
Dengan memahami metode pohon faktor, Anda tidak hanya dapat menemukan KPK dan FPB dengan mudah, tetapi juga mengembangkan pemahaman yang lebih dalam tentang konsep matematika ini. Ingat, latihan adalah kunci! Semakin banyak Anda berlatih, semakin mahir Anda dalam menyelesaikan soal-soal yang berkaitan dengan KPK dan FPB. Selamat belajar!