Contoh soal luas permukaan tabung tanpa tutup – Siapa bilang matematika itu membosankan? Yuk, kita belajar menghitung luas permukaan tabung tanpa tutup! Bayangkan sebuah kaleng tanpa tutupnya, itulah bentuk tabung tanpa tutup yang kita pelajari. Mempelajari cara menghitung luas permukaannya ternyata penting, lho! Misalnya, untuk menentukan berapa banyak cat yang dibutuhkan untuk mengecat tabung tersebut.
Tabung tanpa tutup memiliki bentuk yang unik, hanya terdiri dari alas, selimut, dan tanpa tutup. Untuk menghitung luas permukaannya, kita perlu memahami rumus dan cara mengaplikasikannya. Simak penjelasan berikut untuk memahami konsep dan contoh soal luas permukaan tabung tanpa tutup!
Kesalahan Umum dalam Menghitung Luas Permukaan Tabung Tanpa Tutup
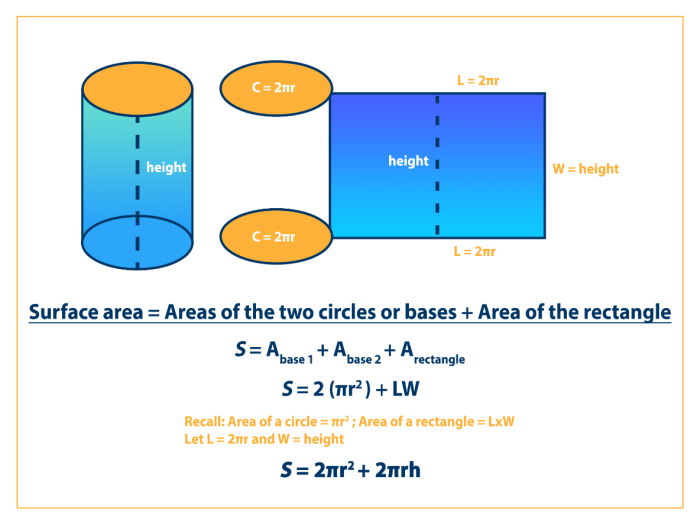
Menghitung luas permukaan tabung tanpa tutup bisa jadi mudah, namun seringkali terjadi kesalahan yang membuat hasil perhitungan menjadi tidak akurat. Kesalahan-kesalahan ini biasanya muncul karena kurangnya pemahaman tentang rumus dan cara mengaplikasikannya pada soal. Berikut adalah 3 kesalahan umum yang sering terjadi dalam menghitung luas permukaan tabung tanpa tutup.
Mencari rumus luas permukaan tabung tanpa tutup? Gampang banget! Ingat aja rumus dasarnya, lalu kurangi dengan luas lingkaran atasnya. Nah, buat yang lagi belajar tentang pajak, kamu bisa cek contoh soal PBB dan jawabannya di situs ini. Setelah memahami konsep pajak, kamu bisa kembali ke soal tabung tanpa tutup dan berlatih menghitung luas permukaannya.
Lupa Menghitung Luas Alas
Kesalahan ini sering terjadi karena fokus utama pada luas selimut tabung. Padahal, luas permukaan tabung tanpa tutup terdiri dari dua bagian, yaitu luas selimut dan luas alas. Luas alas dihitung dengan rumus πr², dimana r adalah jari-jari alas tabung.
- Penyebab: Kurangnya pemahaman tentang definisi luas permukaan tabung tanpa tutup.
- Cara Mengatasi: Pastikan untuk selalu menghitung luas alas dan luas selimut secara terpisah sebelum menjumlahkannya untuk mendapatkan luas permukaan total.
Kesalahan dalam Menghitung Luas Selimut
Luas selimut tabung dihitung dengan rumus 2πrt, dimana r adalah jari-jari alas tabung dan t adalah tinggi tabung. Kesalahan dalam menghitung luas selimut biasanya terjadi karena:
- Salah Menggunakan Rumus: Penggunaan rumus yang salah, seperti menggunakan rumus luas permukaan tabung penuh (2πrh + 2πr²) atau lupa mengalikan dengan 2.
- Kesalahan dalam Menentukan Tinggi: Penggunaan nilai tinggi tabung yang salah atau lupa menentukan nilai tinggi tabung.
Untuk mengatasi kesalahan ini, pastikan untuk memahami rumus luas selimut tabung dengan benar dan teliti dalam menentukan nilai r dan t.
Tidak Memperhatikan Satuan, Contoh soal luas permukaan tabung tanpa tutup
Kesalahan ini sering terjadi ketika nilai r, t, dan π memiliki satuan yang berbeda. Misalnya, jika r dalam cm, t dalam m, dan π menggunakan nilai 3,14, maka hasil perhitungan luas permukaan akan menjadi tidak akurat.
- Penyebab: Kurangnya ketelitian dalam memperhatikan satuan yang digunakan dalam perhitungan.
- Cara Mengatasi: Pastikan semua nilai yang digunakan dalam perhitungan memiliki satuan yang sama. Jika tidak, konversikan nilai tersebut ke dalam satuan yang sama sebelum melakukan perhitungan.
Variasi Soal Luas Permukaan Tabung Tanpa Tutup
Selain soal-soal standar, luas permukaan tabung tanpa tutup dapat disajikan dalam berbagai variasi yang menantang. Variasi ini dapat melibatkan perubahan bentuk soal, seperti penambahan informasi tambahan, penggabungan konsep lain, atau penyajian dalam konteks cerita.
Contoh Soal Variasi
Berikut adalah 2 contoh soal luas permukaan tabung tanpa tutup dengan variasi bentuk soal:
- Sebuah tabung tanpa tutup memiliki diameter alas 14 cm dan tinggi 10 cm. Tabung tersebut akan dicat seluruh permukaannya. Jika biaya pengecatan Rp5.000 per meter persegi, berapa biaya yang dibutuhkan untuk mengecat tabung tersebut?
- Sebuah wadah berbentuk tabung tanpa tutup terbuat dari seng dengan tebal 0,5 cm. Diameter alas wadah tersebut 20 cm dan tingginya 30 cm. Berapa luas seng yang dibutuhkan untuk membuat wadah tersebut, jika diabaikan adanya sambungan?
Pengaruh Variasi Bentuk Soal terhadap Penyelesaian
Variasi bentuk soal dapat mempengaruhi cara penyelesaian dengan beberapa cara:
- Penambahan informasi tambahan: Soal dapat melibatkan informasi tambahan seperti biaya, tebal bahan, atau persentase luas permukaan yang dicat. Hal ini membutuhkan analisis tambahan untuk menentukan langkah-langkah penyelesaian yang tepat.
- Penggabungan konsep lain: Soal dapat menggabungkan konsep lain seperti volume, keliling, atau luas permukaan bangun datar lainnya. Hal ini memerlukan pemahaman yang lebih luas dan kemampuan untuk menghubungkan berbagai konsep.
- Penyajian dalam konteks cerita: Soal dapat disajikan dalam bentuk cerita yang menggambarkan situasi nyata. Hal ini membantu memahami konsep secara lebih holistik dan mengaitkannya dengan kehidupan sehari-hari.
Ilustrasi Variasi Soal dan Penyelesaian
Sebagai contoh, perhatikan soal pertama tentang tabung yang akan dicat. Soal ini melibatkan informasi tambahan berupa biaya pengecatan. Untuk menyelesaikannya, kita perlu:
- Menghitung luas permukaan tabung tanpa tutup menggunakan rumus: Luas Permukaan = 2πr(r + t), di mana r adalah jari-jari alas dan t adalah tinggi tabung.
- Mengubah satuan luas permukaan dari cm2 menjadi m2 karena biaya pengecatan diberikan per meter persegi.
- Mengalikan luas permukaan dalam m2 dengan biaya pengecatan per meter persegi untuk mendapatkan total biaya pengecatan.
Ilustrasi ini menunjukkan bagaimana variasi bentuk soal dapat mempengaruhi langkah-langkah penyelesaian. Dalam kasus ini, informasi tambahan tentang biaya pengecatan mengharuskan kita untuk melakukan konversi satuan dan perhitungan tambahan.
Penutupan Akhir: Contoh Soal Luas Permukaan Tabung Tanpa Tutup
Menghitung luas permukaan tabung tanpa tutup membutuhkan ketelitian dan pemahaman yang mendalam tentang rumus dan komponennya. Dengan latihan dan contoh soal yang beragam, kita akan semakin mahir dalam menguasai konsep ini. Tak hanya dalam matematika, konsep ini juga bermanfaat dalam kehidupan sehari-hari, misalnya dalam menentukan kebutuhan material untuk membuat wadah atau menghitung biaya pengecatan.





