Contoh soal luas dan keliling bangun datar gabungan dan jawabannya – Mengerjakan soal luas dan keliling bangun datar gabungan memang menantang, tapi jangan khawatir! Dengan memahami konsep dasar dan rumus yang tepat, kamu bisa menyelesaikannya dengan mudah. Bayangkan, kamu ingin membuat taman di rumah, bagaimana cara menghitung luas dan keliling taman yang berbentuk gabungan persegi panjang dan segitiga? Nah, dalam artikel ini, kita akan belajar bersama tentang berbagai contoh soal luas dan keliling bangun datar gabungan, lengkap dengan jawabannya.
Kita akan membahas pengertian bangun datar gabungan, rumus menghitung luas dan kelilingnya, contoh soal cerita, dan berbagai tips untuk menyelesaikan soal dengan cepat dan tepat. Siap-siap untuk mengasah kemampuan matematika kamu dan menjelajahi dunia bangun datar gabungan yang menarik!
Contoh Soal Luas dan Keliling Bangun Datar Gabungan
Bangun datar gabungan merupakan gabungan dari dua atau lebih bangun datar sederhana, seperti persegi, persegi panjang, segitiga, lingkaran, dan lain sebagainya. Dalam menghitung luas dan keliling bangun datar gabungan, kita perlu memahami konsep luas dan keliling dari masing-masing bangun datar yang membentuknya.
Contoh Soal Luas Bangun Datar Gabungan Sederhana
Berikut ini contoh soal cerita tentang luas bangun datar gabungan yang sederhana:
- Sebuah taman berbentuk persegi panjang dengan panjang 10 meter dan lebar 5 meter. Di tengah taman tersebut terdapat kolam berbentuk lingkaran dengan diameter 2 meter. Berapakah luas taman yang tidak termasuk kolam?
Untuk menyelesaikan soal ini, kita perlu menghitung luas taman dan luas kolam, kemudian mengurangi luas kolam dari luas taman. Berikut langkah-langkahnya:
- Luas taman = panjang x lebar = 10 meter x 5 meter = 50 meter persegi
- Luas kolam = π x (diameter/2)² = 3,14 x (2 meter/2)² = 3,14 meter persegi
- Luas taman yang tidak termasuk kolam = Luas taman – Luas kolam = 50 meter persegi – 3,14 meter persegi = 46,86 meter persegi
Jadi, luas taman yang tidak termasuk kolam adalah 46,86 meter persegi.
Contoh soal luas dan keliling bangun datar gabungan dan jawabannya memang seru! Kita diajak untuk berpikir kreatif dalam menggabungkan berbagai bentuk geometri. Ingat, kalau kamu menemukan soal yang melibatkan sudut dan arah, bisa jadi kamu perlu mempelajari bentuk polar bilangan kompleks.
Kamu bisa menemukan contoh soal dan pembahasannya di contoh soal bentuk polar bilangan kompleks. Setelah memahami konsep bentuk polar, kamu akan lebih siap untuk menyelesaikan soal-soal luas dan keliling bangun datar gabungan dengan lebih mudah!
Contoh Soal Luas Bangun Datar Gabungan Kompleks
Berikut ini contoh soal cerita tentang luas bangun datar gabungan yang kompleks:
- Sebuah lapangan berbentuk trapesium siku-siku dengan panjang sisi sejajar 20 meter dan 10 meter, tinggi 15 meter, dan panjang sisi miring 17 meter. Di tengah lapangan terdapat taman berbentuk segitiga siku-siku dengan panjang sisi alas 5 meter dan tinggi 12 meter. Berapakah luas lapangan yang tidak termasuk taman?
Untuk menyelesaikan soal ini, kita perlu menghitung luas lapangan dan luas taman, kemudian mengurangi luas taman dari luas lapangan. Berikut langkah-langkahnya:
- Luas lapangan = ½ x (panjang sisi sejajar 1 + panjang sisi sejajar 2) x tinggi = ½ x (20 meter + 10 meter) x 15 meter = 225 meter persegi
- Luas taman = ½ x alas x tinggi = ½ x 5 meter x 12 meter = 30 meter persegi
- Luas lapangan yang tidak termasuk taman = Luas lapangan – Luas taman = 225 meter persegi – 30 meter persegi = 195 meter persegi
Jadi, luas lapangan yang tidak termasuk taman adalah 195 meter persegi.
Contoh Soal Keliling Bangun Datar Gabungan Sederhana
Berikut ini contoh soal cerita tentang keliling bangun datar gabungan yang sederhana:
- Sebuah taman berbentuk persegi panjang dengan panjang 10 meter dan lebar 5 meter. Di tengah taman tersebut terdapat kolam berbentuk lingkaran dengan diameter 2 meter. Berapakah keliling taman yang tidak termasuk kolam?
Untuk menyelesaikan soal ini, kita perlu menghitung keliling taman dan keliling kolam, kemudian mengurangi keliling kolam dari keliling taman. Berikut langkah-langkahnya:
- Keliling taman = 2 x (panjang + lebar) = 2 x (10 meter + 5 meter) = 30 meter
- Keliling kolam = π x diameter = 3,14 x 2 meter = 6,28 meter
- Keliling taman yang tidak termasuk kolam = Keliling taman – Keliling kolam = 30 meter – 6,28 meter = 23,72 meter
Jadi, keliling taman yang tidak termasuk kolam adalah 23,72 meter.
Contoh Soal Keliling Bangun Datar Gabungan Kompleks
Berikut ini contoh soal cerita tentang keliling bangun datar gabungan yang kompleks:
- Sebuah lapangan berbentuk trapesium siku-siku dengan panjang sisi sejajar 20 meter dan 10 meter, tinggi 15 meter, dan panjang sisi miring 17 meter. Di tengah lapangan terdapat taman berbentuk segitiga siku-siku dengan panjang sisi alas 5 meter dan tinggi 12 meter. Berapakah keliling lapangan yang tidak termasuk taman?
Untuk menyelesaikan soal ini, kita perlu menghitung keliling lapangan dan keliling taman, kemudian mengurangi keliling taman dari keliling lapangan. Berikut langkah-langkahnya:
- Keliling lapangan = panjang sisi sejajar 1 + panjang sisi sejajar 2 + tinggi + sisi miring = 20 meter + 10 meter + 15 meter + 17 meter = 62 meter
- Keliling taman = sisi alas + tinggi + sisi miring = 5 meter + 12 meter + 13 meter = 30 meter
- Keliling lapangan yang tidak termasuk taman = Keliling lapangan – Keliling taman = 62 meter – 30 meter = 32 meter
Jadi, keliling lapangan yang tidak termasuk taman adalah 32 meter.
Penerapan Luas dan Keliling Bangun Datar Gabungan dalam Kehidupan Sehari-hari: Contoh Soal Luas Dan Keliling Bangun Datar Gabungan Dan Jawabannya
Konsep luas dan keliling bangun datar gabungan sangat berguna dalam kehidupan sehari-hari. Kita sering kali menemukan bentuk-bentuk gabungan dalam berbagai situasi, mulai dari menghitung luas ruangan hingga menentukan panjang pagar yang dibutuhkan.
Penerapan Luas Bangun Datar Gabungan
Luas bangun datar gabungan dapat digunakan untuk menghitung luas permukaan suatu objek yang terdiri dari beberapa bentuk bangun datar. Berikut beberapa contoh penerapan luas bangun datar gabungan dalam kehidupan sehari-hari:
- Menghitung luas tanah: Jika sebuah tanah berbentuk trapesium dan persegi panjang, maka kita dapat menghitung luas total tanah dengan menjumlahkan luas trapesium dan luas persegi panjang.
- Menghitung luas ruangan: Ruangan rumah seringkali memiliki bentuk yang tidak beraturan, seperti gabungan persegi panjang dan segitiga. Untuk menghitung luas ruangan, kita dapat menghitung luas setiap bentuk bangun datar yang menyusun ruangan tersebut, kemudian menjumlahkannya.
- Menghitung luas lantai: Untuk memasang keramik atau parket pada lantai, kita perlu menghitung luas lantai terlebih dahulu. Jika lantai berbentuk persegi panjang dan terdapat bagian yang berbentuk segitiga, kita perlu menghitung luas masing-masing bentuk dan menjumlahkannya.
Penerapan Keliling Bangun Datar Gabungan
Keliling bangun datar gabungan dapat digunakan untuk menghitung panjang total sisi-sisi dari sebuah objek yang terdiri dari beberapa bentuk bangun datar. Berikut beberapa contoh penerapan keliling bangun datar gabungan dalam kehidupan sehari-hari:
- Menghitung panjang pagar: Jika kita ingin membuat pagar mengelilingi sebuah taman berbentuk persegi panjang dan setengah lingkaran, kita perlu menghitung keliling total dari gabungan bangun datar tersebut.
- Menghitung keliling lapangan: Lapangan olahraga seringkali memiliki bentuk yang tidak beraturan, seperti gabungan persegi panjang dan segitiga. Untuk menghitung keliling lapangan, kita perlu menjumlahkan panjang semua sisi yang membentuk lapangan tersebut.
- Menghitung panjang tali: Jika kita ingin mengikat sebuah benda dengan tali yang berbentuk persegi panjang dan lingkaran, kita perlu menghitung keliling total dari gabungan bangun datar tersebut.
Contoh Penerapan Luas dan Keliling Bangun Datar Gabungan, Contoh soal luas dan keliling bangun datar gabungan dan jawabannya
| No | Situasi | Bangun Datar | Rumus | Contoh Penerapan |
|---|---|---|---|---|
| 1 | Menghitung luas taman | Persegi panjang dan setengah lingkaran | Luas persegi panjang = panjang x lebar Luas setengah lingkaran = 1/2 x π x r² |
Taman berbentuk persegi panjang dengan kolam berbentuk setengah lingkaran di tengahnya. Luas taman dapat dihitung dengan menjumlahkan luas persegi panjang dan luas setengah lingkaran. |
| 2 | Menghitung keliling lapangan | Persegi panjang dan segitiga | Keliling persegi panjang = 2 x (panjang + lebar) Keliling segitiga = sisi 1 + sisi 2 + sisi 3 |
Lapangan sepak bola berbentuk persegi panjang dengan gawang berbentuk segitiga di kedua ujung lapangan. Keliling lapangan dapat dihitung dengan menjumlahkan panjang semua sisi yang membentuk lapangan tersebut. |
| 3 | Menghitung luas ruangan | Persegi panjang dan segitiga | Luas persegi panjang = panjang x lebar Luas segitiga = 1/2 x alas x tinggi |
Ruangan berbentuk persegi panjang dengan jendela berbentuk segitiga di salah satu sudutnya. Luas ruangan dapat dihitung dengan menjumlahkan luas persegi panjang dan luas segitiga. |
Soal Latihan Luas dan Keliling Bangun Datar Gabungan
Bangun datar gabungan merupakan gabungan dari beberapa bangun datar sederhana seperti persegi, persegi panjang, segitiga, dan lingkaran. Untuk menghitung luas dan keliling bangun datar gabungan, kita perlu mengidentifikasi bangun-bangun datar penyusunnya dan kemudian menghitung luas dan keliling masing-masing bangun datar penyusunnya. Setelah itu, kita dapat menjumlahkan luas atau keliling dari semua bangun datar penyusunnya untuk mendapatkan luas atau keliling bangun datar gabungan tersebut.
Soal Latihan Pilihan Ganda
Berikut adalah beberapa contoh soal latihan luas dan keliling bangun datar gabungan dalam bentuk pilihan ganda:
- Perhatikan gambar bangun datar gabungan berikut!
Bangun tersebut terdiri dari sebuah persegi panjang dan sebuah segitiga siku-siku. Panjang persegi panjang adalah 10 cm dan lebarnya 5 cm. Panjang alas segitiga adalah 5 cm dan tingginya 4 cm. Berapakah luas bangun datar gabungan tersebut?
- 50 cm2
- 60 cm2
- 70 cm2
- 80 cm2
Kunci Jawaban: (c) 70 cm2
Penyelesaian:
Luas persegi panjang = panjang x lebar = 10 cm x 5 cm = 50 cm2
Luas segitiga = 1/2 x alas x tinggi = 1/2 x 5 cm x 4 cm = 10 cm2
Luas bangun datar gabungan = luas persegi panjang + luas segitiga = 50 cm2 + 10 cm2 = 70 cm2
- Perhatikan gambar bangun datar gabungan berikut!
Bangun tersebut terdiri dari sebuah persegi dan sebuah setengah lingkaran. Panjang sisi persegi adalah 10 cm. Berapakah keliling bangun datar gabungan tersebut?
- 30 cm
- 40 cm
- 50 cm
- 60 cm
Kunci Jawaban: (b) 40 cm
Penyelesaian:
Keliling persegi = 4 x sisi = 4 x 10 cm = 40 cm
Keliling setengah lingkaran = 1/2 x 2πr = πr = 3,14 x 5 cm = 15,7 cm
Keliling bangun datar gabungan = keliling persegi + keliling setengah lingkaran = 40 cm + 15,7 cm = 55,7 cm
Jadi, keliling bangun datar gabungan tersebut adalah 55,7 cm.
Soal Latihan Essay
Berikut adalah beberapa contoh soal latihan luas dan keliling bangun datar gabungan dalam bentuk essay:
- Sebuah taman berbentuk persegi panjang dengan panjang 20 meter dan lebar 15 meter. Di tengah taman tersebut terdapat kolam berbentuk lingkaran dengan diameter 5 meter. Hitunglah luas taman yang tidak termasuk kolam!
- Sebuah papan berbentuk persegi panjang dengan panjang 12 cm dan lebar 8 cm. Di tengah papan tersebut terdapat sebuah lubang berbentuk segitiga siku-siku dengan panjang alas 6 cm dan tinggi 4 cm. Hitunglah luas papan yang tersisa setelah dipotong!
Soal Latihan Benar-Salah
Berikut adalah beberapa contoh soal latihan luas dan keliling bangun datar gabungan dalam bentuk benar-salah:
- Luas bangun datar gabungan sama dengan jumlah luas dari semua bangun datar penyusunnya. (Benar)
- Keliling bangun datar gabungan sama dengan jumlah keliling dari semua bangun datar penyusunnya. (Salah)
- Untuk menghitung luas bangun datar gabungan, kita hanya perlu mengukur panjang dan lebar bangun datar gabungan tersebut. (Salah)
- Bangun datar gabungan dapat dibentuk dari berbagai macam bangun datar sederhana. (Benar)
Soal Ujian Luas dan Keliling Bangun Datar Gabungan
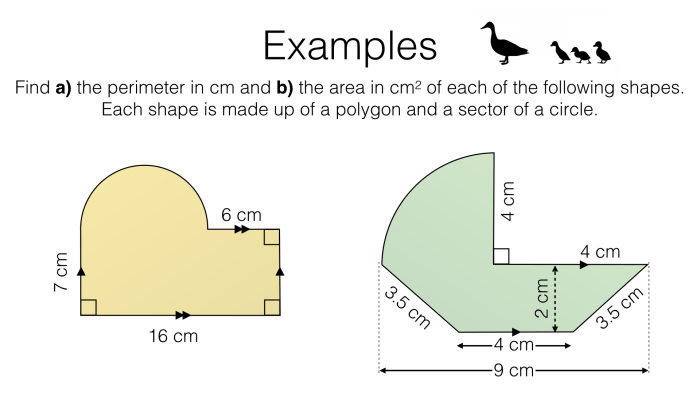
Pada tahap ini, kamu akan menemukan soal-soal yang lebih kompleks dan menantang untuk menguji pemahamanmu tentang luas dan keliling bangun datar gabungan. Soal-soal ini dirancang untuk mengasah kemampuanmu dalam mengidentifikasi bangun-bangun penyusun, menerapkan rumus yang tepat, dan menyelesaikan perhitungan dengan akurat. Mari kita lihat contoh soal-soal berikut:
Soal Pilihan Ganda
Soal pilihan ganda adalah soal yang memberikan beberapa pilihan jawaban, di mana hanya satu jawaban yang benar. Kamu perlu menganalisis soal dan memilih jawaban yang paling tepat berdasarkan pemahamanmu tentang konsep luas dan keliling bangun datar gabungan.
- Sebuah taman berbentuk gabungan persegi panjang dan setengah lingkaran seperti gambar di bawah. Jika panjang taman 20 meter dan lebarnya 14 meter, berapakah luas taman tersebut?
- 280 m2
- 392 m2
- 448 m2
- 560 m2
Jawaban: C. 448 m2
- Perhatikan gambar bangun datar berikut. Jika panjang sisi persegi 10 cm dan jari-jari lingkaran 5 cm, berapakah keliling bangun tersebut?
- 50 cm
- 60 cm
- 70 cm
- 80 cm
Jawaban: B. 60 cm
Soal Essay
Soal essay menuntutmu untuk menjelaskan jawabanmu secara detail dan sistematis. Kamu perlu menunjukkan pemahamanmu tentang konsep luas dan keliling bangun datar gabungan, serta kemampuanmu dalam menyelesaikan masalah dengan langkah-langkah yang tepat.
- Sebuah taman berbentuk gabungan persegi panjang dan segitiga siku-siku seperti gambar di bawah. Jika panjang taman 20 meter, lebarnya 14 meter, dan tinggi segitiga 8 meter, berapakah luas taman tersebut? Jelaskan langkah-langkah penyelesaiannya!
Jawaban:
- Hitung luas persegi panjang: Luas = panjang x lebar = 20 m x 14 m = 280 m2
- Hitung luas segitiga siku-siku: Luas = 1/2 x alas x tinggi = 1/2 x 14 m x 8 m = 56 m2
- Hitung luas total taman: Luas total = Luas persegi panjang + Luas segitiga = 280 m2 + 56 m2 = 336 m2
Jadi, luas taman tersebut adalah 336 m2.
- Perhatikan gambar bangun datar berikut. Jika panjang sisi persegi 10 cm dan jari-jari lingkaran 5 cm, berapakah keliling bangun tersebut? Jelaskan langkah-langkah penyelesaiannya!
Jawaban:
- Hitung keliling persegi: Keliling = 4 x sisi = 4 x 10 cm = 40 cm
- Hitung keliling lingkaran: Keliling = 2 x π x r = 2 x 3,14 x 5 cm = 31,4 cm
- Hitung keliling bangun gabungan: Keliling gabungan = Keliling persegi + Keliling lingkaran – 2 x jari-jari lingkaran = 40 cm + 31,4 cm – 2 x 5 cm = 61,4 cm
Jadi, keliling bangun tersebut adalah 61,4 cm.
Soal Benar-Salah
Soal benar-salah merupakan soal yang mengharuskan kamu untuk menentukan apakah pernyataan yang diberikan benar atau salah. Kamu perlu memahami konsep luas dan keliling bangun datar gabungan dengan baik untuk menjawab soal ini.
- Luas bangun datar gabungan dapat dihitung dengan menjumlahkan luas setiap bangun penyusunnya. (Benar)
- Keliling bangun datar gabungan dapat dihitung dengan menjumlahkan keliling setiap bangun penyusunnya. (Salah)
- Untuk menghitung luas bangun datar gabungan, perlu diketahui bentuk dan ukuran setiap bangun penyusunnya. (Benar)
- Untuk menghitung keliling bangun datar gabungan, hanya perlu diketahui panjang sisi-sisi bangun penyusunnya. (Salah)
Ringkasan Terakhir
Dengan memahami konsep dan rumus luas dan keliling bangun datar gabungan, kamu dapat menyelesaikan berbagai macam soal dengan mudah. Ingat, kunci utama adalah memahami konsep dasar dan latihan yang rutin. Yuk, teruslah berlatih dan tingkatkan kemampuanmu dalam menghitung luas dan keliling bangun datar gabungan! Siapa tahu, kamu bisa menjadi ahli dalam menyelesaikan soal-soal matematika yang menantang!