Contoh soal nilai mutlak kelas 10 kurikulum 2013 – Nilai mutlak, sebuah konsep matematika yang mungkin terdengar asing di telinga, ternyata memiliki peran penting dalam berbagai bidang, mulai dari ilmu fisika hingga ekonomi. Dalam pelajaran matematika kelas 10 kurikulum 2013, kamu akan mempelajari tentang nilai mutlak, sifat-sifatnya, dan bagaimana menyelesaikan persamaan dan pertidaksamaan yang melibatkan nilai mutlak. Mempelajari nilai mutlak tidak hanya tentang angka, tetapi juga tentang memahami bagaimana konsep ini dapat diterapkan dalam memecahkan masalah nyata.
Artikel ini akan membahas berbagai contoh soal nilai mutlak yang sesuai dengan kurikulum 2013 untuk kelas 10. Kamu akan diajak untuk memahami definisi nilai mutlak, sifat-sifatnya, dan bagaimana menyelesaikan berbagai jenis soal yang melibatkan nilai mutlak. Selain itu, artikel ini juga akan menunjukkan bagaimana konsep nilai mutlak dapat diterapkan dalam berbagai bidang lain, seperti fisika, ekonomi, dan teknik. Siap untuk menjelajahi dunia nilai mutlak? Mari kita mulai!
Grafik Fungsi Nilai Mutlak
Fungsi nilai mutlak memiliki karakteristik unik yang memengaruhi bentuk grafiknya. Grafik fungsi nilai mutlak memiliki bentuk V yang simetris terhadap sumbu Y. Untuk memahami bentuk dan sifat grafiknya, kita perlu mempelajari cara menggambarnya dengan benar.
Contoh soal nilai mutlak kelas 10 kurikulum 2013 biasanya mencakup penyelesaian persamaan dan pertidaksamaan nilai mutlak. Nah, kalau kamu udah paham konsep nilai mutlak, coba deh cek contoh soal dan jawaban permutasi untuk mengasah kemampuanmu dalam kombinatorika. Permutasi dan nilai mutlak memang berbeda, tapi keduanya sama-sama penting untuk memahami konsep matematika yang lebih kompleks.
Jadi, yuk, belajar dan berlatih agar kamu semakin mahir dalam matematika!
Cara Menggambar Grafik Fungsi Nilai Mutlak
Berikut adalah langkah-langkah menggambar grafik fungsi nilai mutlak:
- Tentukan titik potong dengan sumbu X. Titik potong dengan sumbu X didapatkan dengan mensubstitusikan y = 0 ke dalam persamaan fungsi dan menyelesaikan persamaan tersebut.
- Tentukan titik potong dengan sumbu Y. Titik potong dengan sumbu Y didapatkan dengan mensubstitusikan x = 0 ke dalam persamaan fungsi.
- Tentukan beberapa titik tambahan dengan mensubstitusikan nilai x lainnya ke dalam persamaan fungsi dan mencari nilai y yang bersesuaian.
- Plot titik-titik yang telah ditemukan pada bidang koordinat.
- Hubungkan titik-titik tersebut dengan garis lurus yang simetris terhadap sumbu Y, membentuk grafik fungsi nilai mutlak.
Contoh Soal
Sebagai contoh, kita akan menggambar grafik fungsi nilai mutlak dengan persamaan y = |x – 2| + 1.
- Tentukan titik potong dengan sumbu X. Substitusikan y = 0 ke dalam persamaan: 0 = |x – 2| + 1. Dengan menyelesaikan persamaan ini, kita dapatkan x = 1 dan x = 3. Jadi, titik potong dengan sumbu X adalah (1, 0) dan (3, 0).
- Tentukan titik potong dengan sumbu Y. Substitusikan x = 0 ke dalam persamaan: y = |0 – 2| + 1. Dengan menyelesaikan persamaan ini, kita dapatkan y = 3. Jadi, titik potong dengan sumbu Y adalah (0, 3).
- Tentukan beberapa titik tambahan. Misalnya, untuk x = -1, y = |-1 – 2| + 1 = 4. Untuk x = 2, y = |2 – 2| + 1 = 1. Untuk x = 4, y = |4 – 2| + 1 = 3. Titik-titik tambahan yang kita dapatkan adalah (-1, 4), (2, 1), dan (4, 3).
- Plot titik-titik yang telah ditemukan pada bidang koordinat.
- Hubungkan titik-titik tersebut dengan garis lurus yang simetris terhadap sumbu Y, membentuk grafik fungsi nilai mutlak y = |x – 2| + 1.
Tabel Contoh Soal dan Solusinya
| No | Persamaan Fungsi | Titik Potong Sumbu X | Titik Potong Sumbu Y | Titik Tambahan | Grafik |
|---|---|---|---|---|---|
| 1 | y = |x| | (0, 0) | (0, 0) | (-1, 1), (1, 1) | [Gambar grafik y = |x|] |
| 2 | y = |x – 1| | (1, 0) | (0, 1) | (0, 1), (2, 1) | [Gambar grafik y = |x – 1|] |
| 3 | y = |x| + 2 | (-2, 0), (2, 0) | (0, 2) | (-1, 3), (1, 3) | [Gambar grafik y = |x| + 2] |
Penerapan Nilai Mutlak dalam Bidang Lainnya
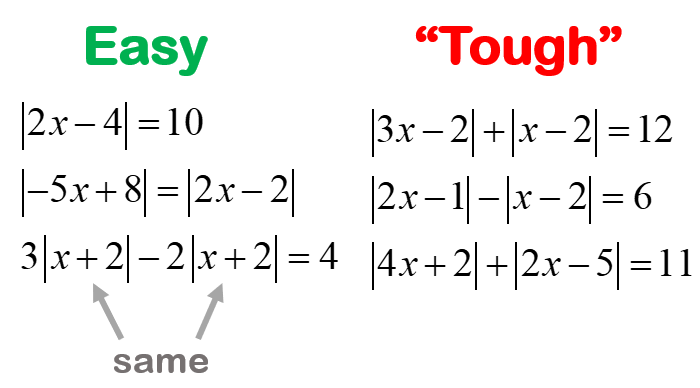
Nilai mutlak, yang didefinisikan sebagai jarak suatu bilangan dari nol, bukan hanya konsep matematika abstrak. Konsep ini memiliki aplikasi praktis dalam berbagai bidang, termasuk fisika, ekonomi, dan teknik. Penerapan nilai mutlak memungkinkan kita untuk mengukur dan menganalisis berbagai fenomena, mulai dari pergerakan objek hingga perubahan harga dan ketahanan material.
Penerapan Nilai Mutlak dalam Fisika
Dalam fisika, nilai mutlak sering digunakan untuk menghitung besarnya besaran fisika, seperti kecepatan, percepatan, dan gaya. Misalnya, kecepatan adalah besaran vektor yang memiliki arah dan besarnya. Nilai mutlak dari kecepatan adalah besarnya kecepatan, yang selalu positif dan menunjukkan seberapa cepat suatu objek bergerak.
- Contoh Soal: Sebuah mobil bergerak ke timur dengan kecepatan 20 meter per detik. Berapakah besarnya kecepatan mobil tersebut?
- Solusi: Besarnya kecepatan mobil adalah |20| = 20 meter per detik.
Penerapan Nilai Mutlak dalam Ekonomi
Dalam ekonomi, nilai mutlak dapat digunakan untuk menganalisis perubahan harga, fluktuasi pasar, dan tingkat keuntungan. Misalnya, jika harga saham suatu perusahaan turun sebesar 10%, nilai mutlak dari perubahan harga adalah 10%, yang menunjukkan besarnya penurunan harga.
- Contoh Soal: Harga saham PT. Maju Bersama pada hari Senin adalah Rp. 10.000. Pada hari Selasa, harga saham turun sebesar 5%. Berapakah besarnya perubahan harga saham tersebut?
- Solusi: Besarnya perubahan harga saham adalah |(Rp. 10.000 x 5%)| = Rp. 500.
Penerapan Nilai Mutlak dalam Teknik, Contoh soal nilai mutlak kelas 10 kurikulum 2013
Dalam teknik, nilai mutlak dapat digunakan untuk menghitung toleransi, kesalahan, dan deviasi. Misalnya, dalam manufaktur, toleransi adalah rentang nilai yang diizinkan untuk suatu dimensi atau karakteristik produk. Nilai mutlak digunakan untuk menentukan seberapa jauh nilai sebenarnya dari suatu produk dapat menyimpang dari nilai yang ditentukan.
- Contoh Soal: Sebuah baut memiliki diameter nominal 10 mm dengan toleransi ±0,5 mm. Berapakah rentang nilai yang diizinkan untuk diameter baut tersebut?
- Solusi: Rentang nilai yang diizinkan adalah 10 mm ± |0,5 mm|, yaitu 9,5 mm hingga 10,5 mm.
Soal Latihan dan Pembahasan
Setelah mempelajari materi nilai mutlak, penting untuk menguji pemahamanmu dengan latihan soal. Berikut beberapa contoh soal latihan yang dapat kamu kerjakan untuk mengasah kemampuanmu dalam menyelesaikan masalah nilai mutlak.
Contoh Soal Latihan Nilai Mutlak
Berikut adalah contoh soal latihan nilai mutlak kelas 10 kurikulum 2013 beserta pembahasannya.
| No. | Soal | Pembahasan |
|---|---|---|
| 1. | Tentukan nilai x yang memenuhi persamaan |x – 2| = 5. | Untuk menyelesaikan persamaan nilai mutlak, kita perlu memisahkan persamaan menjadi dua kasus:
Kasus 1: x – 2 ≥ 0, maka |x – 2| = x – 2 Kasus 2: x – 2 < 0, maka |x – 2| = -(x – 2) Jadi, nilai x yang memenuhi persamaan |x – 2| = 5 adalah x = 7 atau x = -3. |
| 2. | Selesaikan pertidaksamaan |2x + 1| ≤ 3. | Untuk menyelesaikan pertidaksamaan nilai mutlak, kita perlu memisahkan pertidaksamaan menjadi dua kasus:
Kasus 1: 2x + 1 ≥ 0, maka |2x + 1| = 2x + 1 Kasus 2: 2x + 1 < 0, maka |2x + 1| = -(2x + 1) Jadi, solusi pertidaksamaan |2x + 1| ≤ 3 adalah -2 ≤ x ≤ 1. |
| 3. | Tentukan nilai minimum dari fungsi f(x) = |x – 3| + 2. | Fungsi nilai mutlak selalu bernilai non-negatif. Oleh karena itu, nilai minimum dari |x – 3| adalah 0.
Maka, nilai minimum dari f(x) = |x – 3| + 2 adalah 0 + 2 = 2. Nilai minimum ini tercapai ketika x = 3. |
Soal Menantang
Berikut adalah contoh soal yang lebih menantang untuk menguji pemahamanmu lebih dalam tentang nilai mutlak:
Tentukan himpunan penyelesaian dari pertidaksamaan |x² – 4| < |x + 2|.
Soal ini menantang karena melibatkan kombinasi nilai mutlak dan persamaan kuadrat. Untuk menyelesaikannya, kamu perlu menggunakan beberapa teknik, seperti pemfaktoran, pengujian nilai, dan grafik.
Penutup: Contoh Soal Nilai Mutlak Kelas 10 Kurikulum 2013
Memahami konsep nilai mutlak dan penerapannya dalam berbagai bidang adalah langkah penting dalam memahami matematika dan dunia di sekitar kita. Dengan berlatih menyelesaikan berbagai contoh soal nilai mutlak, kamu akan semakin mahir dalam mengaplikasikan konsep ini. Jangan takut untuk bertanya dan mencari bantuan jika kamu menemui kesulitan. Ingat, belajar matematika adalah proses yang berkelanjutan, dan setiap langkah kecil yang kamu ambil akan membantumu mencapai pemahaman yang lebih dalam.






