Contoh soal persamaan trigonometri kelas 11 matematika peminatan – Menjelajahi dunia persamaan trigonometri di kelas 11 matematika peminatan bisa jadi menyenangkan! Kamu akan menemukan banyak sekali aplikasi persamaan trigonometri dalam berbagai bidang, seperti fisika, teknik, dan astronomi. Bayangkan bagaimana kamu bisa menghitung tinggi bangunan dengan menggunakan sudut elevasi, atau bahkan menghitung jarak bintang yang jauh. Dengan memahami persamaan trigonometri, kamu akan membuka pintu menuju pemahaman yang lebih dalam tentang dunia di sekitar kita.
Di sini, kita akan membahas konsep persamaan trigonometri, berbagai metode penyelesaiannya, dan aplikasi praktisnya dalam kehidupan nyata. Siapkan dirimu untuk menjelajahi contoh soal yang menantang dan menarik yang akan membantu kamu menguasai materi trigonometri ini dengan lebih baik.
Pengertian Persamaan Trigonometri
Persamaan trigonometri adalah persamaan yang melibatkan fungsi trigonometri, seperti sinus (sin), cosinus (cos), dan tangen (tan). Persamaan ini umumnya melibatkan variabel sudut yang ingin kita cari nilainya. Dalam konteks matematika kelas 11 peminatan, persamaan trigonometri digunakan untuk menyelesaikan masalah yang berkaitan dengan sudut, panjang sisi, dan hubungan antara sisi-sisi dalam segitiga.
Contoh Persamaan Trigonometri
Berikut adalah beberapa contoh persamaan trigonometri sederhana:
- sin x = 1/2
- cos 2x = -1/2
- tan x = √3
Persamaan-persamaan ini melibatkan fungsi trigonometri yang disamakan dengan suatu nilai konstanta. Tujuannya adalah untuk mencari nilai x (sudut) yang memenuhi persamaan tersebut.
Perbedaan Persamaan Trigonometri dan Identitas Trigonometri
Persamaan trigonometri dan identitas trigonometri merupakan konsep yang berbeda dalam matematika. Berikut adalah perbedaan utamanya:
- Persamaan trigonometri adalah persamaan yang hanya benar untuk nilai-nilai tertentu dari variabel sudut. Contohnya, persamaan sin x = 1/2 hanya benar untuk nilai x = 30° dan x = 150°.
- Identitas trigonometri adalah persamaan yang benar untuk semua nilai variabel sudut. Contohnya, identitas sin² x + cos² x = 1 benar untuk semua nilai x.
Persamaan trigonometri digunakan untuk mencari nilai sudut yang memenuhi persamaan, sedangkan identitas trigonometri digunakan untuk menyederhanakan ekspresi trigonometri atau membuktikan teorema.
Metode Penyelesaian Persamaan Trigonometri: Contoh Soal Persamaan Trigonometri Kelas 11 Matematika Peminatan
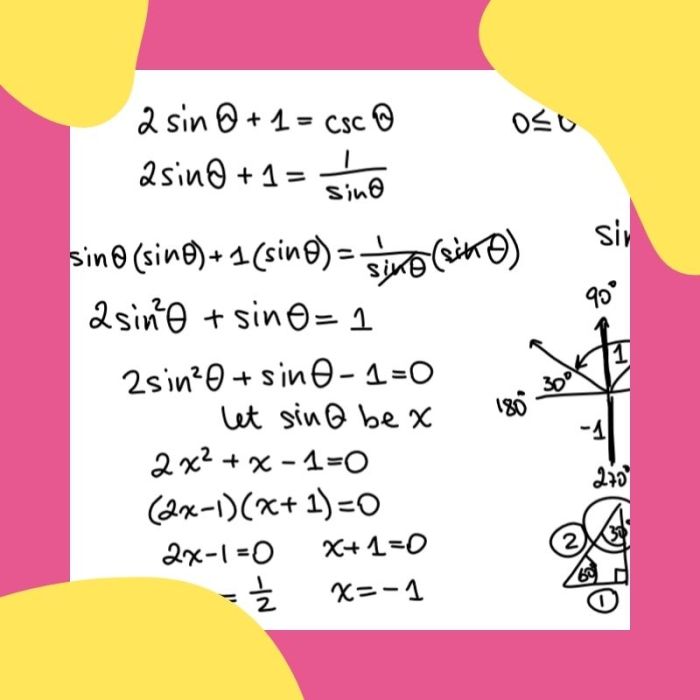
Persamaan trigonometri merupakan persamaan yang memuat fungsi trigonometri seperti sinus, cosinus, dan tangen. Menyelesaikan persamaan trigonometri berarti mencari nilai sudut yang memenuhi persamaan tersebut. Ada berbagai metode yang dapat digunakan untuk menyelesaikan persamaan trigonometri, tergantung pada bentuk persamaannya.
Metode Penyelesaian Persamaan Trigonometri
Berikut adalah beberapa metode umum yang dapat digunakan untuk menyelesaikan persamaan trigonometri:
- Metode Aljabar: Metode ini melibatkan manipulasi aljabar untuk menyederhanakan persamaan trigonometri dan mengisolasi fungsi trigonometri yang ingin kita cari. Metode ini biasanya digunakan untuk menyelesaikan persamaan trigonometri sederhana yang hanya melibatkan satu fungsi trigonometri.
- Metode Substitusi: Metode ini melibatkan substitusi variabel baru untuk mempermudah penyelesaian persamaan trigonometri. Metode ini biasanya digunakan untuk menyelesaikan persamaan trigonometri yang melibatkan fungsi trigonometri ganda, seperti sinus 2x, cosinus 2x, dan tangen 2x.
- Metode Grafik: Metode ini melibatkan plotting grafik fungsi trigonometri dan mencari titik potong grafik dengan garis horizontal yang mewakili nilai konstanta dalam persamaan. Metode ini dapat membantu dalam menemukan solusi numerik untuk persamaan trigonometri yang sulit diselesaikan secara aljabar.
Contoh Soal dan Penyelesaian
Metode Aljabar
Contoh Soal: Tentukan himpunan penyelesaian dari persamaan sin x = 1/2 untuk 0 ≤ x ≤ 2π.
Penyelesaian:
- Identifikasi sudut yang memiliki nilai sinus 1/2. Kita tahu bahwa sin 30° = 1/2 dan sin 150° = 1/2.
- Karena kita mencari solusi dalam rentang 0 ≤ x ≤ 2π, maka kita perlu mencari sudut yang setara dengan 30° dan 150° dalam rentang tersebut.
- Sudut 30° setara dengan 30° (sudut asli) dan 360° – 30° = 330°.
- Sudut 150° setara dengan 150° (sudut asli) dan 360° – 150° = 210°.
- Jadi, himpunan penyelesaian dari persamaan sin x = 1/2 untuk 0 ≤ x ≤ 2π adalah 30°, 150°, 210°, 330°.
Metode Substitusi
Contoh Soal: Tentukan himpunan penyelesaian dari persamaan cos 2x = 1/2 untuk 0 ≤ x ≤ 2π.
Penyelesaian:
- Substitusi variabel baru y = 2x. Persamaan menjadi cos y = 1/2.
- Identifikasi sudut yang memiliki nilai cosinus 1/2. Kita tahu bahwa cos 60° = 1/2 dan cos 300° = 1/2.
- Karena kita mencari solusi dalam rentang 0 ≤ x ≤ 2π, maka kita perlu mencari sudut yang setara dengan 60° dan 300° dalam rentang tersebut.
- Sudut 60° setara dengan 60° (sudut asli) dan 360° – 60° = 300°.
- Sudut 300° setara dengan 300° (sudut asli) dan 360° + 300° = 660°. Karena kita mencari solusi dalam rentang 0 ≤ x ≤ 2π, maka kita hanya perlu mempertimbangkan sudut 300°.
- Kembalikan substitusi y = 2x. Maka kita punya 2x = 60° dan 2x = 300°.
- Selesaikan untuk x. Kita dapatkan x = 30° dan x = 150°. Jadi, himpunan penyelesaian dari persamaan cos 2x = 1/2 untuk 0 ≤ x ≤ 2π adalah 30°, 150°.
Metode Grafik
Contoh Soal: Tentukan himpunan penyelesaian dari persamaan sin x = cos x untuk 0 ≤ x ≤ 2π.
Penyelesaian:
- Plot grafik fungsi y = sin x dan y = cos x dalam rentang 0 ≤ x ≤ 2π.
- Tentukan titik potong kedua grafik. Titik potong tersebut merupakan solusi dari persamaan sin x = cos x.
- Dari grafik, kita dapat melihat bahwa titik potong terjadi pada x = π/4 dan x = 5π/4.
- Jadi, himpunan penyelesaian dari persamaan sin x = cos x untuk 0 ≤ x ≤ 2π adalah π/4, 5π/4.
Persamaan Trigonometri yang Melibatkan Sudut Rangkap
Persamaan trigonometri yang melibatkan sudut rangkap, seperti sinus 2x, cosinus 2x, dan tangen 2x, dapat diselesaikan dengan menggunakan rumus sudut rangkap. Rumus sudut rangkap adalah rumus yang menyatakan hubungan antara fungsi trigonometri sudut rangkap dengan fungsi trigonometri sudut tunggal.
Berikut adalah beberapa rumus sudut rangkap yang dapat digunakan untuk menyelesaikan persamaan trigonometri:
- sin 2x = 2 sin x cos x
- cos 2x = cos² x – sin² x = 1 – 2 sin² x = 2 cos² x – 1
- tan 2x = (2 tan x) / (1 – tan² x)
Contoh Soal: Tentukan himpunan penyelesaian dari persamaan sin 2x = 1/2 untuk 0 ≤ x ≤ 2π.
Penyelesaian:
- Gunakan rumus sin 2x = 2 sin x cos x. Persamaan menjadi 2 sin x cos x = 1/2.
- Bagi kedua ruas dengan 2. Kita dapatkan sin x cos x = 1/4.
- Identifikasi sudut yang memiliki nilai sinus dan cosinus yang memenuhi persamaan sin x cos x = 1/4. Kita tahu bahwa sin 30° = 1/2 dan cos 60° = 1/2. Jadi, sin 30° cos 60° = (1/2) * (1/2) = 1/4.
- Karena kita mencari solusi dalam rentang 0 ≤ x ≤ 2π, maka kita perlu mencari sudut yang setara dengan 30° dan 60° dalam rentang tersebut.
- Sudut 30° setara dengan 30° (sudut asli) dan 360° – 30° = 330°.
- Sudut 60° setara dengan 60° (sudut asli) dan 360° – 60° = 300°.
- Jadi, himpunan penyelesaian dari persamaan sin 2x = 1/2 untuk 0 ≤ x ≤ 2π adalah 30°, 60°, 150°, 210°, 300°, 330°.
Aplikasi Persamaan Trigonometri
Persamaan trigonometri memiliki peran penting dalam berbagai bidang, tidak hanya dalam matematika, tetapi juga dalam ilmu pengetahuan dan teknologi. Kemampuan persamaan trigonometri untuk menghubungkan sudut dan sisi dalam segitiga memungkinkan kita untuk menganalisis dan memecahkan masalah yang melibatkan gerakan berulang, gelombang, dan pola periodik.
Fisika (Gelombang, Getaran)
Persamaan trigonometri digunakan secara luas dalam fisika untuk menggambarkan dan menganalisis fenomena periodik seperti gelombang dan getaran. Fungsi sinus dan cosinus, yang merupakan dasar dari persamaan trigonometri, digunakan untuk memodelkan gerakan harmonik sederhana, seperti gerakan bandul atau pegas.
- Contohnya, persamaan y = A sin(ωt + φ) menggambarkan gerakan harmonik sederhana, di mana A adalah amplitudo, ω adalah frekuensi sudut, t adalah waktu, dan φ adalah fase awal. Persamaan ini membantu kita memahami dan memprediksi gerakan benda yang bergetar.
Teknik (Konstruksi, Mekanika)
Dalam teknik, persamaan trigonometri digunakan untuk berbagai keperluan, seperti perhitungan struktur, desain mesin, dan analisis tegangan. Persamaan trigonometri membantu para insinyur untuk menghitung sudut, panjang, dan kekuatan yang diperlukan untuk membangun struktur yang stabil dan aman.
- Contohnya, dalam konstruksi, persamaan trigonometri digunakan untuk menghitung sudut kemiringan atap, panjang balok penyangga, dan gaya yang bekerja pada struktur.
Astronomi (Gerakan Planet, Bintang)
Persamaan trigonometri digunakan dalam astronomi untuk menentukan posisi planet dan bintang, menghitung jarak antar bintang, dan menganalisis gerakan benda langit. Persamaan trigonometri membantu para astronom untuk memahami dan memprediksi pergerakan benda langit, serta untuk mengukur jarak dan ukuran mereka.
- Contohnya, persamaan trigonometri digunakan untuk menghitung jarak ke bintang menggunakan metode paralaks, di mana sudut yang dibentuk oleh bintang dan Bumi saat Bumi bergerak mengelilingi Matahari diukur.
Contoh Soal, Contoh soal persamaan trigonometri kelas 11 matematika peminatan
Sebuah bangunan memiliki tinggi 20 meter. Seorang pengamat berdiri pada jarak 30 meter dari bangunan dan melihat puncak bangunan dengan sudut elevasi 30 derajat. Hitunglah tinggi pengamat.
- Diketahui: tinggi bangunan (AB) = 20 meter, jarak pengamat (BC) = 30 meter, sudut elevasi (∠ACB) = 30 derajat.
- Ditanya: tinggi pengamat (AC).
- Penyelesaian:
- Perhatikan segitiga ABC, yang merupakan segitiga siku-siku di B.
- Kita dapat menggunakan perbandingan trigonometri tangen untuk mencari panjang AC:
- tan ∠ACB = AB / BC
- tan 30° = 20 / 30
- 1/√3 = 20 / 30
- AC = 20√3 meter.
Diagram Penerapan Persamaan Trigonometri
- Berikut diagram yang menggambarkan penerapan persamaan trigonometri dalam menentukan tinggi suatu bangunan menggunakan sudut elevasi:
- Diagram menunjukkan seorang pengamat yang berdiri pada jarak tertentu dari sebuah bangunan dan melihat puncak bangunan dengan sudut elevasi tertentu.
- Sudut elevasi adalah sudut yang dibentuk oleh garis horizontal dan garis pandang pengamat ke puncak bangunan.
- Dengan menggunakan perbandingan trigonometri tangen, kita dapat menentukan tinggi bangunan dengan mengetahui jarak pengamat dan sudut elevasi.
Soal Latihan Persamaan Trigonometri

Setelah mempelajari berbagai konsep dan teknik dalam menyelesaikan persamaan trigonometri, saatnya untuk mengasah kemampuan dengan mengerjakan soal-soal latihan. Soal latihan ini akan membantu Anda memahami dan mengaplikasikan materi yang telah dipelajari dengan lebih baik.
Soal Latihan
Berikut ini adalah 5 soal latihan persamaan trigonometri dengan tingkat kesulitan yang bervariasi. Soal-soal ini dirancang dengan skenario menarik dan relevan dengan materi kelas 11 peminatan, yang akan membantu Anda dalam memahami aplikasi persamaan trigonometri dalam berbagai bidang.
-
Sebuah bandul sederhana dengan panjang tali 1 meter berayun dengan amplitudo 0,5 meter. Jika periode ayunan bandul adalah 2 detik, tentukan persamaan simpangan bandul sebagai fungsi waktu. Asumsikan bandul berada pada posisi setimbang saat t = 0.
-
Sebuah roda Ferris dengan diameter 50 meter berputar dengan kecepatan sudut konstan 0,1 radian per detik. Jika seorang penumpang berada pada titik tertinggi roda Ferris saat t = 0, tentukan persamaan ketinggian penumpang sebagai fungsi waktu.
-
Tentukan himpunan penyelesaian persamaan trigonometri berikut untuk 0 ≤ x ≤ 2π: sin 2x + cos x = 0.
-
Tentukan nilai x yang memenuhi persamaan trigonometri berikut: tan (x + 30°) = √3.
-
Sebuah pesawat terbang dengan ketinggian 1000 meter di atas permukaan laut melihat dua kapal di laut dengan sudut depresi 30° dan 45°. Jika jarak antara kedua kapal adalah 1000√3 meter, tentukan jarak antara pesawat dengan kedua kapal tersebut.
Solusi Soal Latihan
Berikut adalah solusi lengkap untuk setiap soal latihan yang telah diberikan sebelumnya.
-
Persamaan simpangan bandul sebagai fungsi waktu dapat dinyatakan sebagai:
y(t) = A sin(ωt + φ)
di mana:
- A adalah amplitudo (0,5 meter)
- ω adalah frekuensi sudut (ω = 2π/T = 2π/2 = π radian per detik)
- φ adalah fase awal (φ = 0 karena bandul berada pada posisi setimbang saat t = 0)
Sehingga persamaan simpangan bandul adalah:
y(t) = 0,5 sin(πt)
-
Persamaan ketinggian penumpang sebagai fungsi waktu dapat dinyatakan sebagai:
h(t) = R + R sin(ωt + φ)
di mana:
- R adalah jari-jari roda Ferris (R = 50/2 = 25 meter)
- ω adalah kecepatan sudut (ω = 0,1 radian per detik)
- φ adalah fase awal (φ = 0 karena penumpang berada pada titik tertinggi saat t = 0)
Sehingga persamaan ketinggian penumpang adalah:
h(t) = 25 + 25 sin(0,1t)
-
Untuk menyelesaikan persamaan sin 2x + cos x = 0, kita dapat menggunakan rumus sudut ganda:
sin 2x = 2 sin x cos x
Sehingga persamaan menjadi:
2 sin x cos x + cos x = 0
Faktorisasi persamaan tersebut:
cos x (2 sin x + 1) = 0
Maka solusi persamaan adalah:
- cos x = 0, sehingga x = π/2 atau x = 3π/2
- sin x = -1/2, sehingga x = 7π/6 atau x = 11π/6
Jadi, himpunan penyelesaian persamaan trigonometri adalah π/2, 3π/2, 7π/6, 11π/6.
-
Persamaan tan (x + 30°) = √3 memiliki solusi:
x + 30° = 60° + k180°
di mana k adalah bilangan bulat. Sehingga:
x = 30° + k180°
Jadi, nilai x yang memenuhi persamaan adalah 30° + k180°, dengan k adalah bilangan bulat.
-
Perhatikan gambar berikut:
[Gambar ilustrasi: pesawat di atas laut, dua kapal di bawah pesawat, sudut depresi 30° dan 45° ditunjukkan, jarak antar kapal 1000√3 meter]
Dari gambar, kita dapat menentukan:
- Jarak antara pesawat dan kapal pertama (A) adalah 1000/tan 30° = 1000√3 meter.
- Jarak antara pesawat dan kapal kedua (B) adalah 1000/tan 45° = 1000 meter.
Dengan menggunakan teorema Pythagoras pada segitiga ABC, kita dapat menentukan jarak antara pesawat dan kedua kapal:
AB² = AC² + BC²
Sehingga:
AB² = (1000√3)² + 1000²
AB² = 4000000
AB = 2000 meter
Jadi, jarak antara pesawat dengan kedua kapal adalah 2000 meter.
Akhir Kata

Mempelajari persamaan trigonometri membuka jalan menuju pemahaman yang lebih dalam tentang matematika dan berbagai aplikasi praktisnya dalam kehidupan nyata. Melalui contoh soal yang menarik dan metode penyelesaian yang beragam, kamu dapat mengasah kemampuan berpikir kritis dan analitis. Jangan ragu untuk terus berlatih dan mengeksplorasi dunia trigonometri yang menakjubkan ini!





