Metode matematika, seperti kunci ajaib, membuka jalan menuju pemahaman dan solusi berbagai masalah. Dari perhitungan sederhana hingga analisis rumit, metode matematika telah menjadi alat yang tak ternilai dalam berbagai bidang, mulai dari ilmu pengetahuan dan teknologi hingga ekonomi dan kehidupan sehari-hari.
Perjalanan metode matematika dimulai sejak zaman kuno, di mana para filsuf dan matematikawan pertama kali merumuskan konsep-konsep dasar yang kemudian berkembang menjadi sistematika yang kita kenal sekarang. Seiring berjalannya waktu, metode matematika terus berkembang dan diterapkan dalam berbagai bidang, memicu penemuan-penemuan baru dan kemajuan peradaban.
Sejarah Metode Matematika
Metode matematika, sebagai sistematisasi berpikir logis dan deduktif, telah menjadi landasan bagi berbagai bidang pengetahuan dan teknologi. Perjalanan panjang metode matematika ini telah membentuk dunia kita, mulai dari perhitungan sederhana hingga teori-teori kompleks yang mendasari teknologi modern.
Perkembangan Metode Matematika dari Zaman Kuno hingga Modern
Perkembangan metode matematika dimulai sejak zaman kuno, di mana manusia awal menggunakan konsep dasar seperti penjumlahan, pengurangan, dan pembagian untuk memenuhi kebutuhan sehari-hari. Peradaban Mesopotamia dan Mesir Kuno mengembangkan sistem numerik dan geometri sederhana untuk mengukur lahan, membangun bangunan, dan meramalkan peristiwa astronomi.
Zaman Yunani Kuno menandai tonggak penting dalam sejarah metode matematika. Filsuf dan matematikawan seperti Pythagoras, Euclid, dan Archimedes mengembangkan konsep geometri, teori bilangan, dan kalkulus awal. Karya-karya mereka menjadi dasar bagi perkembangan matematika modern.
Pada abad pertengahan, matematikawan Muslim seperti Al-Khawarizmi dan Ibnu Sina memberikan kontribusi signifikan dalam bidang aljabar, trigonometri, dan astronomi. Karya mereka membantu menyebarkan pengetahuan matematika ke Eropa dan memicu perkembangan ilmu pengetahuan di sana.
Masa Renaissance menandai kebangkitan kembali minat terhadap ilmu pengetahuan klasik, termasuk matematika. Tokoh seperti Leonardo da Vinci, Nicolaus Copernicus, dan Galileo Galilei menerapkan metode matematika dalam penelitian ilmiah mereka, membuka jalan bagi revolusi ilmiah.
Pada abad ke-17, Isaac Newton dan Gottfried Wilhelm Leibniz secara independen mengembangkan kalkulus, sebuah alat matematika yang revolusioner untuk mempelajari perubahan dan gerak. Kalkulus menjadi dasar bagi perkembangan fisika, teknik, dan ekonomi modern.
Pada abad ke-19 dan ke-20, matematika terus berkembang dengan munculnya berbagai bidang baru seperti teori himpunan, logika matematika, dan topologi. Perkembangan ini membuka jalan bagi penerapan metode matematika dalam berbagai bidang seperti ilmu komputer, statistik, dan ekonomi.
Tokoh Penting dalam Sejarah Metode Matematika
Perkembangan metode matematika tidak terlepas dari peran tokoh-tokoh penting yang memberikan kontribusi signifikan dalam berbagai bidang. Berikut adalah beberapa tokoh penting dan kontribusi mereka:
| Tokoh | Kontribusi |
|---|---|
| Pythagoras | Teorema Pythagoras, teori musik, dan filsafat matematika. |
| Euclid | Geometri Euclid, aksioma Euclid, dan “Elemen” yang menjadi dasar geometri selama berabad-abad. |
| Archimedes | Kalkulus awal, metode penentuan luas dan volume, dan prinsip Archimedes. |
| Al-Khawarizmi | Aljabar, sistem numerik desimal, dan buku “Al-Jabr wa al-Muqabalah” yang menjadi dasar aljabar modern. |
| Ibnu Sina | Logika, filsafat, dan matematika, termasuk kontribusi dalam teori bilangan dan geometri. |
| Leonardo da Vinci | Penerapan matematika dalam seni dan teknik, termasuk proporsi, perspektif, dan mekanika. |
| Nicolaus Copernicus | Teori heliosentris, yang mengubah pemahaman tentang tata surya dan menggunakan metode matematika dalam astronomi. |
| Galileo Galilei | Penerapan matematika dalam fisika, termasuk hukum gerak dan astronomi observasional. |
| Isaac Newton | Kalkulus, hukum gravitasi, dan hukum gerak, yang menjadi dasar mekanika klasik. |
| Gottfried Wilhelm Leibniz | Kalkulus, logika matematika, dan sistem biner, yang menjadi dasar ilmu komputer modern. |
Contoh Aplikasi Metode Matematika dalam Berbagai Bidang
Metode matematika memiliki aplikasi luas dalam berbagai bidang, mulai dari ilmu pengetahuan dan teknologi hingga ekonomi dan sosial. Berikut adalah beberapa contoh:
- Ilmu Pengetahuan: Metode matematika digunakan dalam fisika untuk memahami hukum alam, dalam kimia untuk menganalisis reaksi kimia, dan dalam biologi untuk memodelkan sistem biologis.
- Teknologi: Metode matematika digunakan dalam pengembangan komputer, perangkat lunak, dan jaringan komunikasi. Kalkulus digunakan dalam desain mesin dan struktur, sedangkan teori probabilitas digunakan dalam pengembangan algoritma kecerdasan buatan.
- Ekonomi: Metode matematika digunakan dalam analisis ekonomi, peramalan pasar, dan pengambilan keputusan investasi. Model matematika digunakan untuk memahami hubungan antara variabel ekonomi dan memprediksi tren pasar.
Jenis-Jenis Metode Matematika
Metode matematika merupakan alat yang sangat penting dalam memecahkan berbagai masalah dalam berbagai bidang, mulai dari sains dan teknologi hingga ekonomi dan keuangan. Metode ini memungkinkan kita untuk menganalisis data, membangun model, dan membuat prediksi dengan tingkat akurasi yang tinggi. Dalam artikel ini, kita akan menjelajahi berbagai jenis metode matematika berdasarkan prinsip dan penerapannya.
Metode Aljabar
Metode aljabar merupakan salah satu jenis metode matematika yang paling dasar dan banyak digunakan. Metode ini menggunakan simbol dan operasi matematika untuk merepresentasikan dan memecahkan persamaan dan sistem persamaan.
- Metode aljabar memungkinkan kita untuk menemukan nilai yang tidak diketahui dalam persamaan dengan menggunakan operasi matematika seperti penjumlahan, pengurangan, perkalian, dan pembagian.
- Contoh: Dalam persamaan linear sederhana seperti 2x + 3 = 7, kita dapat menggunakan metode aljabar untuk menemukan nilai x dengan mengurangi 3 dari kedua sisi persamaan dan kemudian membagi kedua sisi dengan 2, sehingga menghasilkan x = 2.
Metode Kalkulus, Metode matematika
Metode kalkulus adalah cabang matematika yang berfokus pada perubahan dan gerakan. Metode ini menggunakan konsep limit, turunan, dan integral untuk menganalisis fungsi dan kurva.
- Metode kalkulus sangat penting dalam memahami konsep kecepatan, percepatan, dan perubahan dalam berbagai bidang seperti fisika, teknik, dan ekonomi.
- Contoh: Dalam fisika, metode kalkulus digunakan untuk menghitung kecepatan dan percepatan benda yang bergerak, sedangkan dalam ekonomi, metode ini digunakan untuk menganalisis pertumbuhan ekonomi dan perubahan harga.
Metode Statistik
Metode statistik merupakan metode yang digunakan untuk mengumpulkan, menganalisis, dan menginterpretasikan data. Metode ini menggunakan berbagai teknik untuk mengidentifikasi pola, tren, dan hubungan dalam data.
- Metode statistik sangat berguna dalam berbagai bidang seperti ilmu sosial, kesehatan, dan bisnis untuk memahami data dan membuat keputusan yang didasarkan pada bukti.
- Contoh: Dalam ilmu sosial, metode statistik digunakan untuk menganalisis survei dan data demografi, sedangkan dalam kesehatan, metode ini digunakan untuk menganalisis data klinis dan penelitian.
Metode Numerik
Metode numerik merupakan metode yang menggunakan pendekatan numerik untuk memecahkan masalah matematika yang rumit. Metode ini menggunakan algoritma dan komputer untuk menghasilkan solusi aproksimasi yang akurat.
- Metode numerik sangat berguna dalam berbagai bidang seperti ilmu komputer, teknik, dan keuangan untuk menyelesaikan persamaan diferensial, memodelkan sistem kompleks, dan membuat simulasi.
- Contoh: Dalam ilmu komputer, metode numerik digunakan untuk mengembangkan algoritma untuk pemrosesan gambar dan pengenalan pola, sedangkan dalam teknik, metode ini digunakan untuk memodelkan perilaku struktur dan sistem mekanik.
Metode Geometri
Metode geometri merupakan metode yang mempelajari bentuk, ukuran, dan posisi objek dalam ruang. Metode ini menggunakan konsep titik, garis, bidang, dan bentuk geometri lainnya untuk memecahkan masalah.
- Metode geometri sangat penting dalam berbagai bidang seperti arsitektur, teknik, dan desain untuk membangun struktur, merencanakan proyek, dan membuat objek dengan bentuk dan ukuran yang tepat.
- Contoh: Dalam arsitektur, metode geometri digunakan untuk mendesain bangunan dan struktur, sedangkan dalam teknik, metode ini digunakan untuk mendesain mesin dan peralatan.
Metode Probabilitas dan Statistika
Metode probabilitas dan statistika merupakan metode yang mempelajari peluang dan kejadian acak. Metode ini menggunakan konsep probabilitas, distribusi probabilitas, dan uji hipotesis untuk menganalisis data dan membuat prediksi.
- Metode ini sangat penting dalam berbagai bidang seperti ilmu sosial, ekonomi, dan keuangan untuk memahami risiko dan ketidakpastian, serta membuat keputusan yang didasarkan pada data dan probabilitas.
- Contoh: Dalam ilmu sosial, metode ini digunakan untuk menganalisis data survei dan perilaku manusia, sedangkan dalam ekonomi, metode ini digunakan untuk menganalisis pasar keuangan dan risiko investasi.
Metode Optimasi
Metode optimasi merupakan metode yang mencari solusi terbaik untuk masalah yang melibatkan kendala dan tujuan. Metode ini menggunakan berbagai teknik matematika untuk menemukan solusi optimal yang memaksimalkan atau meminimalkan fungsi objektif.
- Metode optimasi sangat penting dalam berbagai bidang seperti teknik, ekonomi, dan keuangan untuk merancang sistem, membuat keputusan, dan mengalokasikan sumber daya secara optimal.
- Contoh: Dalam teknik, metode optimasi digunakan untuk merancang struktur yang kuat dan efisien, sedangkan dalam ekonomi, metode ini digunakan untuk memaksimalkan keuntungan dan meminimalkan biaya.
Perbandingan Metode Matematika
| Metode | Keunggulan | Kelemahan |
|---|---|---|
| Aljabar | Sederhana dan mudah dipahami. Dapat digunakan untuk memecahkan berbagai masalah matematika. | Tidak dapat memecahkan masalah yang kompleks atau yang melibatkan fungsi non-linear. |
| Kalkulus | Dapat digunakan untuk menganalisis fungsi dan kurva dengan tingkat akurasi yang tinggi. Sangat penting dalam memahami konsep perubahan dan gerakan. | Membutuhkan pemahaman konsep matematika yang lebih tinggi. Tidak dapat memecahkan masalah yang melibatkan data yang tidak berkelanjutan. |
| Statistika | Dapat digunakan untuk menganalisis data dan membuat keputusan yang didasarkan pada bukti. Sangat berguna dalam memahami pola, tren, dan hubungan dalam data. | Membutuhkan data yang besar dan akurat. Tidak dapat memecahkan masalah yang melibatkan hubungan sebab-akibat yang kompleks. |
| Numerik | Dapat digunakan untuk memecahkan masalah matematika yang rumit dengan pendekatan numerik. Sangat berguna dalam memodelkan sistem kompleks dan membuat simulasi. | Membutuhkan komputer dan algoritma yang kompleks. Solusi yang dihasilkan hanya aproksimasi. |
| Geometri | Dapat digunakan untuk memecahkan masalah yang melibatkan bentuk, ukuran, dan posisi objek. Sangat penting dalam membangun struktur dan membuat objek dengan bentuk dan ukuran yang tepat. | Tidak dapat memecahkan masalah yang melibatkan fungsi non-linear atau data yang tidak berkelanjutan. |
| Probabilitas dan Statistika | Dapat digunakan untuk menganalisis data dan membuat prediksi yang didasarkan pada peluang. Sangat berguna dalam memahami risiko dan ketidakpastian. | Membutuhkan data yang besar dan akurat. Tidak dapat memecahkan masalah yang melibatkan hubungan sebab-akibat yang kompleks. |
| Optimasi | Dapat digunakan untuk menemukan solusi terbaik untuk masalah yang melibatkan kendala dan tujuan. Sangat berguna dalam merancang sistem, membuat keputusan, dan mengalokasikan sumber daya secara optimal. | Membutuhkan algoritma yang kompleks dan waktu komputasi yang lama. Tidak dapat memecahkan masalah yang melibatkan fungsi objektif yang tidak kontinu. |
Aplikasi Metode Matematika dalam Berbagai Bidang
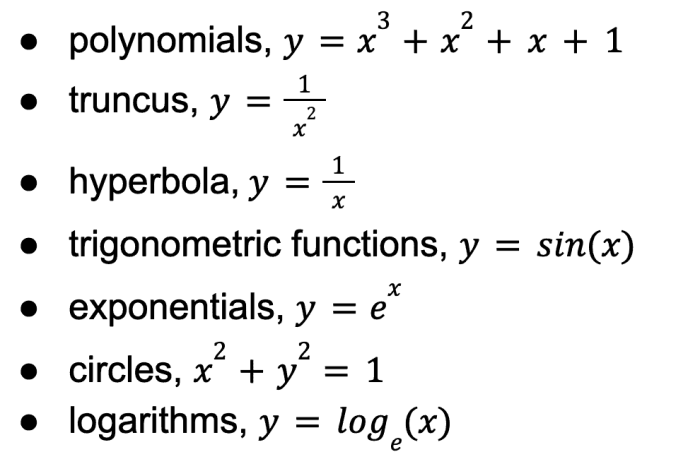
Metode matematika merupakan alat yang ampuh dalam memahami dan menyelesaikan berbagai masalah di dunia. Aplikasi metode matematika tidak terbatas pada bidang matematika murni, tetapi juga merambah ke berbagai bidang lainnya, seperti sains, teknologi, ekonomi, dan sosial. Metode matematika membantu kita dalam merumuskan masalah, menganalisis data, dan menemukan solusi yang efektif.
Aplikasi Metode Matematika dalam Sains
Metode matematika berperan penting dalam pengembangan ilmu pengetahuan, khususnya dalam bidang sains. Metode ini memungkinkan para ilmuwan untuk merumuskan teori, menguji hipotesis, dan memprediksi hasil eksperimen.
- Contohnya, dalam fisika, kalkulus digunakan untuk mempelajari gerak benda, medan gravitasi, dan energi.
- Dalam kimia, persamaan diferensial digunakan untuk memodelkan reaksi kimia dan menentukan laju reaksi.
- Dalam biologi, statistika digunakan untuk menganalisis data genetik dan mempelajari evolusi makhluk hidup.
Aplikasi Metode Matematika dalam Teknologi
Metode matematika menjadi pondasi dalam pengembangan teknologi modern. Metode ini digunakan dalam berbagai bidang teknologi, seperti pemrosesan sinyal, komputasi, dan desain.
- Contohnya, dalam bidang komputer, algoritma matematika digunakan untuk mengembangkan perangkat lunak dan sistem operasi.
- Dalam bidang telekomunikasi, teori informasi digunakan untuk mengoptimalkan transmisi data dan mengurangi noise.
- Dalam bidang robotika, metode matematika digunakan untuk merancang robot yang dapat bergerak dan berinteraksi dengan lingkungannya.
Aplikasi Metode Matematika dalam Ekonomi
Metode matematika digunakan secara luas dalam bidang ekonomi untuk menganalisis data ekonomi, merumuskan model ekonomi, dan memprediksi tren ekonomi.
- Contohnya, ekonometri digunakan untuk menguji hubungan antara variabel ekonomi dan membuat prediksi tentang pertumbuhan ekonomi.
- Teori permainan digunakan untuk menganalisis interaksi antara pelaku ekonomi dan memprediksi hasil dari persaingan pasar.
- Analisis data ekonomi menggunakan metode statistik untuk memahami pola konsumsi, investasi, dan perdagangan.
Aplikasi Metode Matematika dalam Sosial
Metode matematika juga digunakan dalam bidang sosial untuk mempelajari perilaku manusia, interaksi sosial, dan dinamika sosial.
- Contohnya, dalam sosiologi, statistika digunakan untuk menganalisis data demografi dan mempelajari perubahan sosial.
- Dalam psikologi, metode matematika digunakan untuk mempelajari perilaku manusia dan merancang eksperimen untuk menguji teori psikologi.
- Dalam ilmu politik, teori permainan digunakan untuk menganalisis interaksi antara aktor politik dan memprediksi hasil dari pemilihan umum.
“Matematika adalah bahasa yang digunakan untuk mengungkapkan hukum alam.” – Galileo Galilei
“Matematika adalah alat yang paling ampuh untuk memahami dunia di sekitar kita.” – Albert Einstein
Prinsip dan Konsep Dasar Metode Matematika
Metode matematika merupakan alat yang ampuh untuk memahami dan menyelesaikan masalah di berbagai bidang, mulai dari ilmu pengetahuan alam hingga ilmu sosial. Metode ini didasari oleh prinsip-prinsip dasar yang memungkinkan kita untuk berpikir logis dan sistematis, serta menggunakan konsep-konsep matematika yang tepat untuk mencapai solusi yang akurat. Dalam artikel ini, kita akan menjelajahi prinsip dan konsep dasar yang mendasari metode matematika.
Logika, Deduksi, dan Induksi
Metode matematika berakar pada logika, yang merupakan sistem berpikir yang didasarkan pada aturan-aturan tertentu untuk mencapai kesimpulan yang valid. Logika matematika membantu kita untuk menalar dengan benar dan membangun argumen yang kuat. Dua jenis penalaran yang penting dalam metode matematika adalah deduksi dan induksi.
- Deduksi adalah proses penalaran yang dimulai dari premis umum dan kemudian menarik kesimpulan khusus. Misalnya, jika kita tahu bahwa semua manusia adalah makhluk hidup, dan bahwa Socrates adalah manusia, maka kita dapat menyimpulkan bahwa Socrates adalah makhluk hidup. Deduksi sering digunakan dalam pembuktian matematika, di mana kita menggunakan teorema yang sudah diketahui untuk membuktikan teorema baru.
- Induksi adalah proses penalaran yang dimulai dari pengamatan khusus dan kemudian menarik kesimpulan umum. Misalnya, jika kita mengamati bahwa beberapa bilangan genap dapat dibagi dengan 2, dan kemudian kita melihat bahwa semua bilangan genap yang kita amati dapat dibagi dengan 2, maka kita dapat menyimpulkan bahwa semua bilangan genap dapat dibagi dengan 2. Induksi sering digunakan dalam ilmu pengetahuan alam, di mana kita mengumpulkan data dari eksperimen dan kemudian menarik kesimpulan umum tentang fenomena yang diamati.
Konsep Dasar dalam Metode Matematika
Metode matematika menggunakan berbagai konsep dasar yang penting untuk memahami dan menyelesaikan masalah. Beberapa konsep dasar yang penting meliputi:
- Variabel adalah simbol yang mewakili suatu nilai yang dapat berubah. Variabel digunakan untuk menyatakan besaran yang tidak diketahui dalam persamaan atau fungsi. Misalnya, dalam persamaan x + 2 = 5, x adalah variabel yang mewakili nilai yang tidak diketahui.
- Persamaan adalah pernyataan matematis yang menyatakan bahwa dua ekspresi sama. Persamaan digunakan untuk menyelesaikan masalah yang melibatkan variabel yang tidak diketahui. Misalnya, persamaan 2x + 3 = 7 dapat digunakan untuk menemukan nilai x yang memenuhi persamaan tersebut.
- Fungsi adalah hubungan matematis yang menghubungkan setiap nilai input dengan satu nilai output. Fungsi digunakan untuk memodelkan hubungan antara variabel yang berbeda. Misalnya, fungsi f(x) = x² menghubungkan setiap nilai x dengan kuadratnya.
Penerapan Prinsip dan Konsep Dasar dalam Pemecahan Masalah
Prinsip dan konsep dasar metode matematika diterapkan dalam berbagai cara untuk memecahkan masalah. Misalnya, dalam menyelesaikan masalah matematika, kita dapat menggunakan logika deduktif untuk mengidentifikasi informasi yang relevan dan menarik kesimpulan yang valid. Kita juga dapat menggunakan konsep variabel, persamaan, dan fungsi untuk memodelkan masalah dan menemukan solusi.
Misalnya, perhatikan masalah berikut: “Sebuah toko menjual apel dengan harga Rp 5.000 per kg. Jika seseorang membeli 3 kg apel, berapa total harga yang harus dibayar?”. Untuk menyelesaikan masalah ini, kita dapat menggunakan konsep variabel, persamaan, dan fungsi.
Misalkan x adalah total harga yang harus dibayar. Kita dapat memodelkan masalah ini dengan persamaan x = 5000 * 3. Dalam persamaan ini, x adalah variabel yang mewakili total harga, 5000 adalah harga per kg apel, dan 3 adalah jumlah apel yang dibeli. Dengan menyelesaikan persamaan ini, kita dapat menemukan bahwa total harga yang harus dibayar adalah Rp 15.000.
Contoh Penerapan Metode Matematika dalam Kehidupan Sehari-hari
Metode matematika bukan hanya materi pelajaran yang rumit di sekolah. Faktanya, matematika hadir dalam berbagai aspek kehidupan sehari-hari, membantu kita menyelesaikan masalah, membuat keputusan, dan memahami dunia di sekitar kita. Dari menghitung uang belanja hingga merencanakan perjalanan, matematika berperan penting dalam kehidupan kita.
Perhitungan Keuangan
Matematika sangat penting dalam mengelola keuangan pribadi dan bisnis. Contohnya, ketika kita berbelanja, kita menggunakan matematika untuk menghitung total biaya, menghitung diskon, dan membandingkan harga. Dalam berinvestasi, matematika membantu kita menghitung pengembalian investasi, risiko, dan pertumbuhan portofolio.
- Menghitung total biaya belanja dan diskon.
- Membandingkan harga dan memilih produk terbaik.
- Menghitung bunga pinjaman dan cicilan.
- Merencanakan anggaran dan pengeluaran.
- Membuat keputusan investasi yang bijak.
Pengukuran dan Geometri
Matematika, khususnya geometri, digunakan dalam berbagai aktivitas yang melibatkan pengukuran dan dimensi. Misalnya, ketika kita membangun rumah, kita menggunakan geometri untuk menghitung luas tanah, volume ruangan, dan panjang material bangunan. Dalam desain interior, kita menggunakan geometri untuk menentukan ukuran furnitur, mengatur tata letak ruangan, dan memilih dekorasi yang tepat.
- Menghitung luas tanah dan ruangan.
- Merencanakan tata letak ruangan dan desain interior.
- Membuat peta dan denah.
- Menghitung jarak dan waktu tempuh.
- Mendesain objek dan struktur.
Pengambilan Keputusan
Metode matematika membantu kita dalam pengambilan keputusan yang rasional dan logis. Contohnya, ketika kita memilih jalur tercepat untuk menuju tempat tujuan, kita menggunakan konsep jarak, waktu, dan kecepatan. Dalam memilih investasi, kita menggunakan analisis statistik dan probabilitas untuk memperkirakan risiko dan potensi keuntungan.
- Memilih jalur tercepat dan terhemat untuk bepergian.
- Menganalisis data dan membuat keputusan bisnis.
- Memprediksi tren dan peluang.
- Menilai risiko dan peluang dalam investasi.
- Mengoptimalkan sumber daya dan efisiensi.
Statistik dan Probabilitas
Statistik dan probabilitas membantu kita memahami dan menganalisis data, serta membuat prediksi. Contohnya, dalam dunia kesehatan, statistik digunakan untuk menganalisis data pasien, mengidentifikasi pola penyakit, dan mengembangkan pengobatan yang efektif. Dalam bidang bisnis, statistik digunakan untuk menganalisis data penjualan, mengidentifikasi tren pasar, dan membuat strategi pemasaran yang tepat.
- Menganalisis data dan mengidentifikasi pola.
- Membuat prediksi dan perencanaan.
- Mengembangkan strategi pemasaran dan bisnis.
- Menilai efektivitas program dan kebijakan.
- Membuat keputusan berdasarkan data dan analisis.
Teknologi dan Komputasi
Matematika merupakan dasar dari teknologi dan komputasi. Algoritma, pemrograman, dan desain komputer semua didasarkan pada prinsip-prinsip matematika. Contohnya, komputer menggunakan kalkulus untuk menghasilkan gambar 3D yang realistis, dan algoritma matematika digunakan dalam mesin pencari untuk menemukan informasi yang relevan.
- Desain dan pengembangan perangkat lunak.
- Pemrosesan data dan informasi.
- Kecerdasan buatan dan pembelajaran mesin.
- Grafik komputer dan animasi.
- Kriptografi dan keamanan data.
Akhir Kata

Metode matematika, dengan kekuatannya dalam mengungkap pola dan hubungan, membuka cakrawala baru dalam memahami dunia. Melalui aplikasi yang luas dan beragam, metode matematika menjadi bukti nyata bagaimana pemikiran logis dan analitis dapat membawa kita menuju solusi yang inovatif dan efektif.





