Matematika, sebuah ilmu yang seringkali dianggap rumit dan menakutkan, ternyata memiliki peran penting dalam kehidupan kita. Konsep matematika merupakan dasar dari berbagai ilmu pengetahuan dan teknologi yang kita gunakan sehari-hari. Dari menghitung uang belanja hingga merancang gedung pencakar langit, matematika selalu hadir di sekitar kita.
Dalam artikel ini, kita akan menjelajahi dunia konsep matematika, mulai dari pengertian dasar hingga penerapannya dalam berbagai bidang. Kita akan melihat bagaimana konsep matematika berkembang dari masa ke masa dan bagaimana perkembangan teknologi memengaruhi perkembangannya. Siap-siap untuk menemukan sisi menarik dari matematika yang mungkin belum pernah Anda ketahui sebelumnya!
Pengertian Konsep Matematika
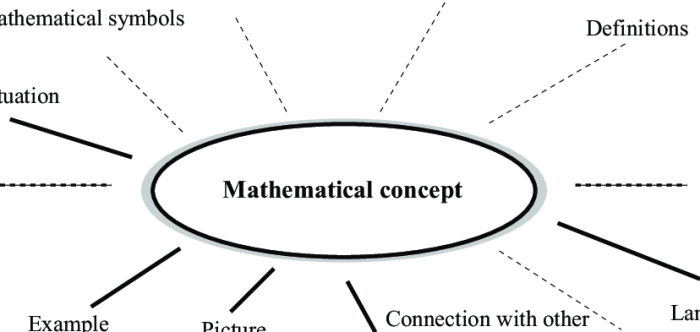
Konsep matematika merupakan dasar dari semua pembelajaran matematika. Konsep ini merupakan ide atau gagasan abstrak yang mendasari pemahaman tentang suatu objek, hubungan, atau operasi dalam matematika.
Konsep matematika dapat diibaratkan seperti batu bata yang digunakan untuk membangun sebuah bangunan. Tanpa batu bata, bangunan tidak akan berdiri kokoh. Begitu pula dengan matematika, tanpa pemahaman yang kuat tentang konsep-konsep dasar, maka pemahaman terhadap materi matematika yang lebih kompleks akan menjadi sulit.
Contoh Konsep Matematika dalam Kehidupan Sehari-hari
Konsep matematika hadir dalam berbagai aspek kehidupan kita. Berikut beberapa contohnya:
- Ketika kita berbelanja, kita menggunakan konsep bilangan untuk menghitung jumlah barang dan uang yang harus dibayarkan.
- Saat kita memasak, kita menggunakan konsep pengukuran untuk menentukan takaran bahan makanan yang tepat.
- Dalam berkendara, kita menggunakan konsep kecepatan, jarak, dan waktu untuk menentukan waktu tempuh dan mengantisipasi potensi bahaya.
Jenis-jenis Konsep Matematika
Konsep matematika dapat dikategorikan menjadi beberapa jenis, antara lain:
- Konsep Bilangan: Konsep ini meliputi pengertian tentang bilangan bulat, pecahan, desimal, dan bilangan real. Contohnya, kita menggunakan konsep bilangan bulat untuk menghitung jumlah orang dalam sebuah ruangan.
- Konsep Geometri: Konsep ini mencakup pengertian tentang bentuk, ukuran, dan posisi objek di ruang. Contohnya, kita menggunakan konsep geometri untuk menentukan luas dan keliling suatu ruangan.
- Konsep Aljabar: Konsep ini berkaitan dengan penggunaan simbol dan operasi untuk menyelesaikan persamaan dan pertidaksamaan. Contohnya, kita menggunakan konsep aljabar untuk menghitung biaya total pembelian berdasarkan harga per unit dan jumlah unit yang dibeli.
- Konsep Statistika: Konsep ini membahas tentang pengumpulan, pengolahan, dan interpretasi data. Contohnya, kita menggunakan konsep statistika untuk menganalisis hasil survei tentang kepuasan pelanggan.
- Konsep Kalkulus: Konsep ini mempelajari tentang perubahan dan pergerakan. Contohnya, kita menggunakan konsep kalkulus untuk menghitung kecepatan dan percepatan suatu objek.
Perbedaan Konsep Matematika dan Konsep Non-Matematika
Konsep matematika memiliki karakteristik yang membedakannya dari konsep non-matematika. Berikut tabel yang menampilkan perbedaannya:
| Aspek | Konsep Matematika | Konsep Non-Matematika |
|---|---|---|
| Sifat | Abstrak, universal, dan objektif | Konkret, spesifik, dan subjektif |
| Pembuktian | Dapat dibuktikan secara logis dan matematis | Bersifat interpretatif dan bergantung pada persepsi |
| Aplikasi | Dapat diterapkan dalam berbagai bidang ilmu dan teknologi | Terbatas pada bidang tertentu |
Peran Konsep Matematika

Matematika adalah bahasa universal yang mendasari banyak aspek kehidupan kita. Konsep-konsep matematika tidak hanya hadir dalam bidang-bidang ilmu pengetahuan yang eksak, tetapi juga merambah ke berbagai bidang lainnya, bahkan dalam kehidupan sehari-hari.
Peran Konsep Matematika dalam Ilmu Pengetahuan
Konsep matematika merupakan fondasi bagi berbagai disiplin ilmu pengetahuan.
- Dalam ilmu fisika, matematika digunakan untuk merumuskan hukum-hukum alam, seperti hukum gravitasi Newton dan hukum gerak Newton.
- Dalam ilmu kimia, matematika digunakan untuk menghitung reaksi kimia, menentukan konsentrasi larutan, dan menganalisis struktur molekul.
- Dalam ilmu biologi, matematika digunakan untuk memodelkan pertumbuhan populasi, menganalisis data genetik, dan mempelajari interaksi antar organisme.
- Dalam ilmu ekonomi, matematika digunakan untuk menganalisis pasar, memprediksi pertumbuhan ekonomi, dan mengelola keuangan.
Penggunaan Konsep Matematika dalam Teknologi
Konsep matematika memainkan peran penting dalam pengembangan teknologi modern.
- Dalam bidang komputer, konsep matematika seperti aljabar linier, kalkulus, dan teori probabilitas digunakan untuk mengembangkan algoritma, membangun sistem operasi, dan mendesain perangkat keras.
- Dalam bidang telekomunikasi, konsep matematika digunakan untuk mengkode dan mendekode sinyal, membangun jaringan komunikasi, dan meningkatkan kualitas sinyal.
- Dalam bidang robotika, konsep matematika digunakan untuk mengendalikan gerakan robot, memproses informasi sensor, dan menavigasi lingkungan.
Konsep Matematika dalam Kehidupan Sehari-hari
Konsep matematika tidak hanya berperan dalam ilmu pengetahuan dan teknologi, tetapi juga membantu kita dalam menyelesaikan masalah sehari-hari.
- Ketika berbelanja, kita menggunakan konsep matematika untuk menghitung total harga, menentukan diskon, dan membandingkan harga.
- Ketika memasak, kita menggunakan konsep matematika untuk mengukur bahan makanan, menentukan waktu memasak, dan menghitung kalori.
- Ketika bepergian, kita menggunakan konsep matematika untuk menghitung jarak, waktu tempuh, dan biaya perjalanan.
Peran Konsep Matematika dalam Berbagai Profesi
| Profesi | Peran Konsep Matematika |
|---|---|
| Insinyur | Menggunakan kalkulus, aljabar linier, dan geometri untuk mendesain struktur, mesin, dan sistem. |
| Akuntan | Menggunakan aritmatika, aljabar, dan statistik untuk mengelola keuangan, menganalisis data, dan membuat laporan keuangan. |
| Dokter | Menggunakan statistik dan probabilitas untuk menganalisis data medis, mendiagnosis penyakit, dan menentukan pengobatan. |
| Arsitek | Menggunakan geometri, trigonometri, dan aljabar linier untuk mendesain bangunan, merencanakan tata ruang, dan menghitung material. |
Pengembangan Konsep Matematika
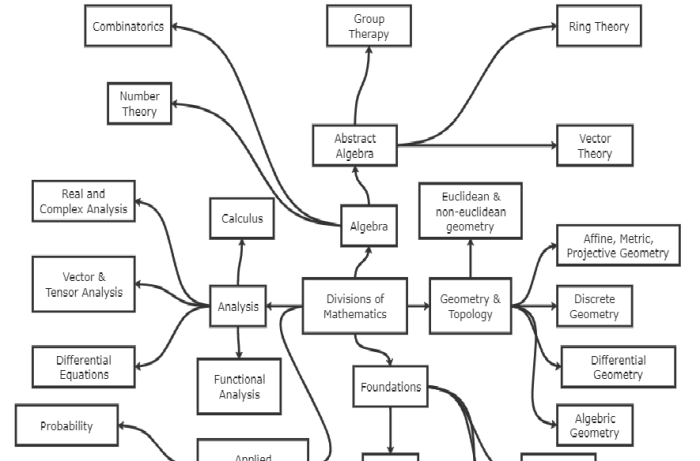
Matematika, sebagai bahasa universal yang mendasari berbagai bidang ilmu pengetahuan, telah mengalami evolusi yang panjang dan menarik. Perjalanan pengembangan konsep matematika ini diwarnai oleh kontribusi para pemikir brilian dari berbagai zaman, yang membawa kita pada pemahaman yang lebih dalam tentang dunia di sekitar kita.
Tahap-Tahap Pengembangan Konsep Matematika
Pengembangan konsep matematika dapat dibagi menjadi beberapa tahap, yang ditandai oleh penemuan dan pemikiran baru yang mendalam. Berikut adalah garis besar tahap-tahap tersebut:
- Zaman Kuno (Sebelum 500 SM): Pada periode ini, matematika berkembang secara empiris, didorong oleh kebutuhan praktis dalam perdagangan, pengukuran, dan konstruksi. Bangsa Mesopotamia dan Mesir Kuno telah mengembangkan sistem bilangan, geometri dasar, dan aljabar sederhana. Bangsa Babilonia, misalnya, mengembangkan sistem bilangan berbasis 60 yang masih digunakan dalam pengukuran waktu dan sudut hingga saat ini.
- Zaman Yunani Kuno (500 SM – 300 M): Zaman ini menandai tonggak penting dalam sejarah matematika. Para filsuf Yunani seperti Thales, Pythagoras, dan Euclid, mentransformasi matematika dari ilmu praktis menjadi ilmu deduktif. Mereka mengembangkan konsep-konsep geometri, teori bilangan, dan logika, yang membentuk dasar matematika modern.
- Zaman Pertengahan (300 M – 1400 M): Selama periode ini, matematika berkembang terutama di dunia Islam, di mana para ilmuwan seperti Al-Khawarizmi dan Ibnu Sina membuat kemajuan signifikan dalam aljabar, trigonometri, dan astronomi. Al-Khawarizmi, misalnya, dikenal sebagai “Bapak Aljabar” karena kontribusinya dalam memecahkan persamaan aljabar.
- Zaman Renaisans (1400 M – 1600 M): Renaisans menandai kebangkitan kembali minat terhadap ilmu pengetahuan klasik di Eropa. Para ilmuwan seperti Leonardo da Vinci, Nicolaus Copernicus, dan Galileo Galilei, menggunakan matematika sebagai alat untuk memahami alam semesta. Galileo, misalnya, menggunakan matematika untuk mendefinisikan hukum gerak dan menemukan hukum gravitasi.
- Zaman Pencerahan (1600 M – 1800 M): Pada periode ini, matematika berkembang pesat dengan munculnya kalkulus, teori probabilitas, dan geometri analitik. Isaac Newton dan Gottfried Wilhelm Leibniz secara independen mengembangkan kalkulus, yang merupakan alat penting dalam fisika, teknik, dan ilmu komputer.
- Zaman Modern (1800 M – Sekarang): Abad ke-19 dan ke-20 menandai munculnya berbagai cabang matematika baru, seperti geometri non-Euclidean, topologi, dan teori himpunan. Perkembangan ini dipicu oleh kebutuhan untuk memahami konsep-konsep baru dalam fisika, ekonomi, dan ilmu komputer. Perkembangan teori kuantum di abad ke-20, misalnya, membutuhkan pengembangan konsep matematika baru untuk memahami perilaku partikel subatom.
Tokoh-Tokoh Penting dalam Pengembangan Konsep Matematika
Banyak tokoh yang telah memberikan kontribusi signifikan dalam pengembangan konsep matematika. Berikut adalah beberapa di antaranya:
- Euclid (300 SM): Dikenal sebagai “Bapak Geometri”, Euclid menulis “Elemen”, sebuah buku yang menjadi dasar geometri selama berabad-abad. Dalam bukunya, Euclid mendefinisikan konsep-konsep geometri dasar seperti titik, garis, dan bidang, dan membuktikan teorema-teorema penting seperti teorema Pythagoras.
- Al-Khawarizmi (820 M): Seorang ilmuwan Persia yang dikenal sebagai “Bapak Aljabar”. Dia menulis buku “Al-Jabr wa al-Muqabala” yang membahas tentang cara menyelesaikan persamaan aljabar. Karyanya sangat berpengaruh dalam perkembangan aljabar di dunia Islam dan Eropa.
- Isaac Newton (1643-1727): Seorang ilmuwan Inggris yang dikenal karena penemuannya tentang hukum gravitasi dan kalkulus. Newton menggunakan kalkulus untuk memecahkan masalah fisika, seperti menentukan gerak planet dan gaya gravitasi.
- Gottfried Wilhelm Leibniz (1646-1716): Seorang matematikawan dan filsuf Jerman yang secara independen mengembangkan kalkulus. Leibniz juga mengembangkan notasi kalkulus yang masih digunakan hingga saat ini.
- Bernhard Riemann (1826-1866): Seorang matematikawan Jerman yang dikenal karena pengembangan geometri non-Euclidean. Geometri non-Euclidean memainkan peran penting dalam pengembangan teori relativitas umum Einstein.
- David Hilbert (1862-1943): Seorang matematikawan Jerman yang dikenal karena pekerjaannya dalam teori himpunan, aljabar, dan logika. Hilbert mengemukakan serangkaian masalah matematika yang disebut “Masalah Hilbert”, yang telah mendorong penelitian matematika selama berabad-abad.
Pengaruh Perkembangan Teknologi terhadap Pengembangan Konsep Matematika
Perkembangan teknologi telah memainkan peran penting dalam pengembangan konsep matematika. Berikut adalah beberapa contohnya:
- Kalkulator dan Komputer: Kalkulator dan komputer telah membantu matematikawan untuk menyelesaikan masalah yang rumit dan melakukan perhitungan yang kompleks dengan lebih cepat dan akurat. Perkembangan komputer juga memungkinkan para matematikawan untuk mengeksplorasi konsep-konsep matematika yang sebelumnya tidak dapat diakses.
- Internet dan Jaringan Komputer: Internet dan jaringan komputer telah memfasilitasi kolaborasi dan pertukaran informasi di antara para matematikawan di seluruh dunia. Ini telah mempercepat laju pengembangan konsep matematika dan memungkinkan para matematikawan untuk membangun di atas pekerjaan satu sama lain.
- Pemrosesan Data dan Analisis Statistik: Perkembangan teknologi pemrosesan data dan analisis statistik telah membuka peluang baru dalam matematika. Para matematikawan sekarang dapat menganalisis kumpulan data yang besar dan kompleks, yang memungkinkan mereka untuk menemukan pola dan tren yang sebelumnya tidak terlihat.
Garis Waktu Pengembangan Konsep Matematika
| Zaman | Periode | Perkembangan Penting | Tokoh Penting |
|---|---|---|---|
| Zaman Kuno | Sebelum 500 SM | Sistem bilangan, geometri dasar, aljabar sederhana | Bangsa Mesopotamia, Bangsa Mesir Kuno, Bangsa Babilonia |
| Zaman Yunani Kuno | 500 SM – 300 M | Geometri, teori bilangan, logika | Thales, Pythagoras, Euclid |
| Zaman Pertengahan | 300 M – 1400 M | Aljabar, trigonometri, astronomi | Al-Khawarizmi, Ibnu Sina |
| Zaman Renaisans | 1400 M – 1600 M | Geometri, astronomi, mekanika | Leonardo da Vinci, Nicolaus Copernicus, Galileo Galilei |
| Zaman Pencerahan | 1600 M – 1800 M | Kalkulus, teori probabilitas, geometri analitik | Isaac Newton, Gottfried Wilhelm Leibniz |
| Zaman Modern | 1800 M – Sekarang | Geometri non-Euclidean, topologi, teori himpunan, analisis data, ilmu komputer | Bernhard Riemann, David Hilbert, Alan Turing, John von Neumann |
Penerapan Konsep Matematika
Matematika merupakan ilmu yang mendasari banyak aspek kehidupan. Konsep-konsep matematika, seperti aljabar, geometri, kalkulus, dan statistika, memiliki peran penting dalam memecahkan berbagai masalah dan memahami berbagai fenomena. Penerapan konsep matematika dapat ditemukan dalam berbagai bidang, mulai dari ilmu pengetahuan, teknologi, ekonomi, hingga seni dan budaya.
Cara Menerapkan Konsep Matematika dalam Menyelesaikan Masalah
Penerapan konsep matematika dalam menyelesaikan masalah dimulai dengan memahami masalah yang ingin dipecahkan. Setelah itu, kita perlu menentukan konsep matematika yang relevan dengan masalah tersebut. Konsep matematika yang dipilih kemudian diterapkan untuk memodelkan masalah, menganalisis data, dan menemukan solusi.
- Identifikasi masalah dan definisikan variabel-variabel yang terlibat.
- Tentukan konsep matematika yang relevan untuk memodelkan masalah.
- Terapkan konsep matematika untuk menganalisis data dan menemukan solusi.
- Evaluasi solusi dan interpretasikan hasilnya dalam konteks masalah.
Penerapan Konsep Matematika dalam Bidang Ekonomi
Konsep matematika banyak diterapkan dalam bidang ekonomi untuk menganalisis data, membuat prediksi, dan mengambil keputusan. Misalnya, dalam bidang ekonomi, konsep matematika digunakan untuk:
- Analisis Permintaan dan Penawaran: Konsep fungsi dan persamaan linear digunakan untuk memodelkan hubungan antara permintaan dan penawaran suatu produk. Dengan menggunakan konsep ini, ekonom dapat memprediksi harga keseimbangan suatu produk dan menentukan faktor-faktor yang mempengaruhi permintaan dan penawaran.
- Analisis Investasi: Konsep matematika seperti kalkulus dan statistika digunakan untuk menganalisis risiko dan keuntungan investasi. Analisis ini membantu investor untuk membuat keputusan investasi yang lebih tepat dan meminimalkan risiko kerugian.
- Analisis Pertumbuhan Ekonomi: Konsep matematika digunakan untuk memodelkan pertumbuhan ekonomi suatu negara. Dengan menggunakan model matematika, ekonom dapat memprediksi pertumbuhan ekonomi di masa depan dan menganalisis faktor-faktor yang mempengaruhinya.
Penerapan Konsep Matematika dalam Arsitektur
Konsep matematika, khususnya geometri, memiliki peran penting dalam arsitektur. Arsitek menggunakan prinsip-prinsip geometri untuk mendesain bangunan yang kokoh, estetis, dan fungsional.
Contohnya, konsep geometri digunakan dalam menentukan bentuk dan ukuran bangunan, mengkalkulasi luas dan volume ruangan, serta merancang struktur bangunan yang kuat dan tahan lama.
Langkah-langkah Menggunakan Konsep Matematika untuk Membuat Model Simulasi
Model simulasi adalah representasi matematika dari sistem nyata yang digunakan untuk memprediksi perilaku sistem tersebut. Model simulasi dapat digunakan untuk berbagai tujuan, seperti:
- Menguji berbagai skenario: Model simulasi dapat digunakan untuk menguji berbagai skenario dan memprediksi dampaknya terhadap sistem.
- Menganalisis kinerja sistem: Model simulasi dapat digunakan untuk menganalisis kinerja sistem dan mengidentifikasi area yang perlu ditingkatkan.
- Merencanakan strategi: Model simulasi dapat digunakan untuk merencanakan strategi dan memprediksi hasil dari strategi tersebut.
Berikut adalah langkah-langkah umum dalam membuat model simulasi menggunakan konsep matematika:
- Definisi Masalah: Tentukan masalah yang ingin dipecahkan dengan model simulasi.
- Identifikasi Variabel: Tentukan variabel-variabel yang terlibat dalam masalah dan hubungan di antara mereka.
- Pemilihan Model Matematika: Pilih model matematika yang sesuai dengan masalah dan variabel yang terlibat.
- Pembuatan Model: Buat model matematika berdasarkan konsep matematika yang dipilih.
- Validasi Model: Validasi model dengan data nyata untuk memastikan akurasi dan relevansi model.
- Simulasi: Jalankan simulasi dengan menggunakan model matematika untuk memprediksi perilaku sistem.
- Analisis dan Interpretasi: Analisis hasil simulasi dan interpretasikan hasilnya dalam konteks masalah.
Kesimpulan: Konsep Matematika
Konsep matematika adalah pondasi yang kokoh untuk memahami dunia di sekitar kita. Dari membantu kita memecahkan masalah sehari-hari hingga mendorong inovasi di berbagai bidang, matematika terus berperan penting dalam membentuk peradaban manusia. Dengan memahami konsep matematika, kita dapat membuka pintu menuju berbagai peluang dan penemuan baru. Jadi, jangan takut untuk menjelajahi dunia matematika dan menemukan keajaibannya!





