Dot product, dalam matematika, merupakan operasi aljabar yang menggabungkan dua vektor dan menghasilkan skalar. Operasi ini memiliki banyak aplikasi dalam bidang ilmu pengetahuan dan teknologi, seperti fisika, geometri, dan ilmu komputer. Dalam artikel ini, kita akan menjelajahi contoh soal dot product untuk memahami konsep dan penerapannya.
Dot product memberikan informasi tentang bagaimana dua vektor saling berhubungan, seperti besar proyeksi satu vektor pada vektor lainnya atau besar sudut antara keduanya. Dengan memahami konsep dot product, kita dapat menganalisis berbagai fenomena dan menyelesaikan masalah-masalah kompleks dalam berbagai bidang.
Pengertian Dot Product
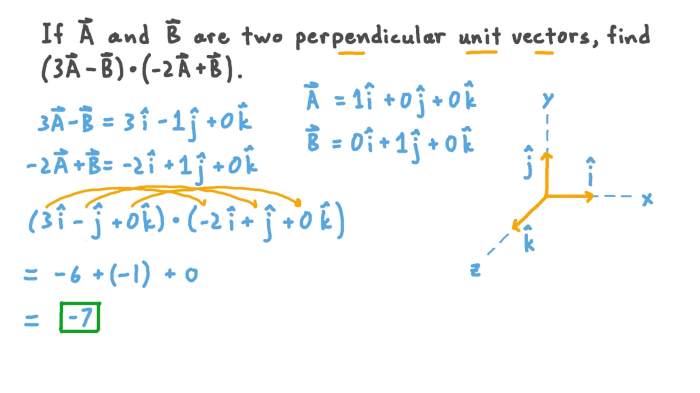
Dot product, juga dikenal sebagai perkalian skalar, merupakan operasi matematika yang menggabungkan dua vektor dan menghasilkan nilai skalar. Nilai skalar ini mewakili proyeksi satu vektor ke vektor lainnya, atau dengan kata lain, sejauh mana kedua vektor searah. Dot product digunakan dalam berbagai bidang seperti fisika, geometri, dan pemrosesan gambar.
Definisi Dot Product
Dalam matematika, dot product dari dua vektor didefinisikan sebagai hasil kali komponen-komponen yang sesuai dari kedua vektor, kemudian dijumlahkan. Secara formal, dot product dari vektor a = (a1, a2, …, an) dan b = (b1, b2, …, bn) didefinisikan sebagai:
a · b = a1b1 + a2b2 + … + anbn
Sifat-Sifat Dot Product
Dot product memiliki beberapa sifat penting yang perlu diketahui, antara lain:
- Komutatif: a · b = b · a
- Distributif: a · (b + c) = a · b + a · c
- Asosiatif dengan perkalian skalar: (ka) · b = k(a · b) = a · (kb)
- Hubungan dengan panjang vektor: a · a = ||a||2, dimana ||a|| adalah panjang vektor a.
Contoh Ilustrasi Dot Product dengan Vektor Dua Dimensi
Misalkan kita memiliki dua vektor dua dimensi: a = (3, 4) dan b = (1, 2). Dot product dari kedua vektor ini dapat dihitung sebagai berikut:
a · b = (3)(1) + (4)(2) = 3 + 8 = 11
Hasil dot product ini adalah nilai skalar 11. Nilai ini menunjukkan proyeksi vektor a ke vektor b, atau sebaliknya, proyeksi vektor b ke vektor a. Semakin besar nilai dot product, semakin searah kedua vektor.
Rumus Dot Product
Dot product, atau produk skalar, adalah operasi matematika yang menghasilkan skalar (nilai tunggal) dari dua vektor. Hasil dot product ini memberikan informasi tentang bagaimana dua vektor tersebut saling berhubungan. Dot product memiliki aplikasi yang luas dalam berbagai bidang seperti fisika, matematika, dan ilmu komputer.
Rumus Umum Dot Product
Rumus umum dot product dua vektor, a dan b, adalah:
a · b = ||a|| ||b|| cos θ
di mana:
- a · b adalah dot product dari vektor a dan b.
- ||a|| dan ||b|| adalah besar (magnitudo) vektor a dan b.
- θ adalah sudut antara vektor a dan b.
Menghitung Dot Product Menggunakan Komponen Vektor
Dot product juga dapat dihitung dengan menggunakan komponen vektor. Jika vektor a = (a1, a2, a3) dan vektor b = (b1, b2, b3), maka dot product mereka dapat dihitung sebagai:
a · b = a1b1 + a2b2 + a3b3
Contoh Perhitungan Dot Product
Misalkan kita memiliki dua vektor, a = (2, 3, 1) dan b = (1, -2, 4). Untuk menghitung dot product dari kedua vektor ini, kita dapat menggunakan rumus komponen vektor:
a · b = (2)(1) + (3)(-2) + (1)(4) = 2 – 6 + 4 = 0
Hasil dot product adalah 0, yang menunjukkan bahwa kedua vektor tersebut saling tegak lurus (sudut antara mereka adalah 90 derajat).
Penerapan Dot Product
Dot product, selain memberikan informasi tentang proyeksi satu vektor pada vektor lainnya, juga memiliki aplikasi luas dalam berbagai bidang ilmu pengetahuan dan teknologi. Penggunaan dot product memungkinkan kita untuk memahami dan menyelesaikan masalah yang berkaitan dengan geometri, fisika, dan bidang lainnya.
Menentukan Sudut Antara Dua Vektor
Salah satu aplikasi penting dot product adalah untuk menentukan sudut antara dua vektor. Rumus dot product yang melibatkan sudut antara dua vektor memungkinkan kita untuk menghitung sudut tersebut secara akurat.
Rumus dot product yang melibatkan sudut:
a ⋅ b = |a| |b| cos θ
Dimana:
- a ⋅ b adalah dot product dari vektor a dan b.
- |a| adalah panjang vektor a.
- |b| adalah panjang vektor b.
- θ adalah sudut antara vektor a dan b.
Dengan menggunakan rumus ini, kita dapat menentukan sudut antara dua vektor dengan menghitung dot product mereka dan membagi hasilnya dengan perkalian panjang kedua vektor tersebut. Kemudian, kita dapat menggunakan fungsi cosinus invers untuk mendapatkan sudut tersebut.
Aplikasi Dot Product dalam Fisika
Dot product memiliki aplikasi yang luas dalam fisika, terutama dalam konsep kerja. Kerja yang dilakukan oleh gaya pada suatu objek didefinisikan sebagai dot product dari gaya dan perpindahan objek tersebut.
Rumus kerja:
W = F ⋅ d
Dimana:
- W adalah kerja yang dilakukan.
- F adalah gaya yang bekerja pada objek.
- d adalah perpindahan objek.
Jika gaya dan perpindahan sejajar, kerja yang dilakukan adalah maksimum. Jika gaya dan perpindahan tegak lurus, kerja yang dilakukan adalah nol. Hal ini menunjukkan bagaimana dot product membantu kita memahami hubungan antara gaya, perpindahan, dan kerja.
Aplikasi Dot Product dalam Berbagai Bidang
| Bidang | Aplikasi Dot Product |
|---|---|
| Fisika | Menghitung kerja, energi potensial, dan fluks energi. |
| Matematika | Menentukan proyeksi vektor, menghitung jarak titik ke bidang, dan mengidentifikasi vektor ortogonal. |
| Komputer Grafis | Menghitung pencahayaan, menghitung normal permukaan, dan menentukan sudut antara objek. |
| Kecerdasan Buatan | Menghitung kesamaan antara dua vektor, seperti dalam algoritma machine learning. |
| Teknik | Menganalisis tegangan dan deformasi dalam struktur, menghitung aliran fluida, dan merancang sistem kontrol. |
Contoh Soal Dot Product
Dot product adalah operasi matematika yang menghasilkan skalar dari dua vektor. Operasi ini sangat berguna dalam berbagai bidang, seperti fisika, geometri, dan ilmu komputer. Dalam konteks ini, kita akan membahas beberapa contoh soal dot product dengan tingkat kesulitan yang berbeda.
Contoh Soal Dot Product
Berikut ini adalah tiga contoh soal dot product dengan tingkat kesulitan yang berbeda, beserta penyelesaian dan jawabannya.
| Soal | Penyelesaian | Jawaban |
|---|---|---|
| Hitunglah dot product dari vektor a = (2, 3) dan b = (4, 1). |
Dot product dari dua vektor a = (a1, a2) dan b = (b1, b2) didefinisikan sebagai:
Dengan demikian, dot product dari vektor a = (2, 3) dan b = (4, 1) adalah:
|
11 |
| Tentukan sudut antara vektor u = (1, 2, 3) dan v = (4, 5, 6). |
Sudut antara dua vektor u dan v dapat dihitung menggunakan rumus:
Dimana:
Pertama, hitung dot product dari u dan v:
Kemudian, hitung panjang vektor u dan v:
Substitusikan nilai-nilai tersebut ke dalam rumus:
Oleh karena itu, sudut antara u dan v adalah:
|
16.26° |
| Tentukan proyeksi ortogonal vektor a = (1, 2, 3) pada vektor b = (4, 5, 6). |
Proyeksi ortogonal vektor a pada vektor b adalah vektor yang sejajar dengan b dan memiliki panjang yang sama dengan panjang proyeksi a pada b. Proyeksi ini dapat dihitung dengan rumus:
Pertama, hitung dot product dari a dan b:
Kemudian, hitung panjang vektor b:
Substitusikan nilai-nilai tersebut ke dalam rumus:
|
(128/77, 160/77, 192/77) |
Contoh Soal Dot Product dengan Vektor
Dot product adalah operasi matematika yang menghasilkan skalar dari dua vektor. Hasil dot product menunjukkan hubungan antara kedua vektor, seperti seberapa sejajar atau tegak lurus keduanya. Pada contoh ini, kita akan membahas dot product pada vektor dua dimensi.
Contoh Soal Dot Product dengan Vektor Dua Dimensi
Misalkan kita memiliki dua vektor dua dimensi, yaitu:
- Vektor A = (2, 3)
- Vektor B = (4, 1)
Tentukan hasil dot product dari kedua vektor tersebut.
Langkah-Langkah Penyelesaian
Untuk menyelesaikan dot product, kita dapat menggunakan rumus berikut:
A · B = (a1 * b1) + (a2 * b2)
di mana:
- A = (a1, a2)
- B = (b1, b2)
Dengan menggunakan rumus tersebut, kita dapat menghitung dot product dari vektor A dan B:
A · B = (2 * 4) + (3 * 1) = 8 + 3 = 11
Jadi, hasil dot product dari vektor A dan B adalah 11.
Ilustrasi Gambar, Contoh soal dot product
Ilustrasi gambar di bawah ini menunjukkan vektor A dan B serta hasil dot product-nya.
Gambar tersebut menampilkan dua vektor A dan B dalam koordinat kartesius. Vektor A memiliki titik awal di (0, 0) dan titik akhir di (2, 3). Vektor B memiliki titik awal di (0, 0) dan titik akhir di (4, 1). Garis putus-putus menunjukkan proyeksi vektor A ke arah vektor B. Panjang proyeksi tersebut menunjukkan hasil dot product dari kedua vektor.
Contoh Soal Dot Product dengan Matriks
Dot product, atau perkalian titik, adalah operasi matematika yang menggabungkan dua vektor dan menghasilkan skalar. Dalam konteks matriks, dot product dapat diterapkan pada baris dan kolom matriks, menghasilkan matriks baru. Operasi ini memiliki berbagai aplikasi dalam matematika, fisika, dan ilmu komputer.
Contoh Soal Dot Product dengan Matriks
Misalnya, kita ingin mencari dot product dari dua matriks berikut:
Matriks A:
| 1 | 2 |
| 3 | 4 |
Matriks B:
| 5 | 6 |
| 7 | 8 |
Cara Menghitung Dot Product Matriks
Untuk menghitung dot product matriks, kita perlu mengalikan setiap elemen dari baris pertama matriks A dengan elemen yang sesuai pada kolom pertama matriks B, kemudian menjumlahkan hasil perkalian tersebut. Proses ini diulang untuk setiap kombinasi baris matriks A dan kolom matriks B.
Berikut adalah langkah-langkah untuk menghitung dot product dari matriks A dan B:
- Elemen pertama dari matriks hasil adalah dot product dari baris pertama matriks A dan kolom pertama matriks B: (1 * 5) + (2 * 7) = 19.
- Elemen kedua dari matriks hasil adalah dot product dari baris pertama matriks A dan kolom kedua matriks B: (1 * 6) + (2 * 8) = 22.
- Elemen ketiga dari matriks hasil adalah dot product dari baris kedua matriks A dan kolom pertama matriks B: (3 * 5) + (4 * 7) = 43.
- Elemen keempat dari matriks hasil adalah dot product dari baris kedua matriks A dan kolom kedua matriks B: (3 * 6) + (4 * 8) = 50.
Jadi, dot product dari matriks A dan B adalah:
| 19 | 22 |
| 43 | 50 |
Soal Dot Product dengan Vektor dan Skalar
Dalam matematika, dot product merupakan operasi aljabar yang menghasilkan skalar dari dua vektor. Operasi ini sering digunakan dalam berbagai bidang, seperti fisika, geometri, dan ilmu komputer. Salah satu contoh penggunaan dot product adalah untuk menghitung proyeksi vektor pada vektor lainnya. Dot product juga dapat digunakan untuk menentukan sudut antara dua vektor.
Contoh Soal Dot Product dengan Vektor dan Skalar
Berikut ini adalah contoh soal dot product dengan vektor dan skalar:
- Diketahui vektor a = (2, 3, 1) dan skalar k = 5. Hitunglah dot product dari a dan k.
Cara Menghitung Dot Product Vektor dan Skalar
Untuk menghitung dot product dari vektor a dan skalar k, kita dapat menggunakan rumus berikut:
a ⋅ k = ka
Rumus ini menunjukkan bahwa dot product dari vektor a dan skalar k sama dengan perkalian skalar k dengan vektor a. Dengan kata lain, kita hanya perlu mengalikan setiap komponen vektor a dengan skalar k.
Ilustrasi Gambar, Contoh soal dot product
Untuk menggambarkan vektor, skalar, dan hasil dot product, perhatikan ilustrasi gambar berikut:
Gambar tersebut menunjukkan vektor a = (2, 3, 1) dan skalar k = 5. Hasil dot product dari a dan k adalah ka = (10, 15, 5). Vektor ka memiliki arah yang sama dengan vektor a, tetapi magnitudonya lima kali lebih besar.
Soal Dot Product dengan Aplikasi Fisika
Dot product merupakan operasi matematika yang sangat berguna dalam fisika, khususnya dalam menghitung kerja yang dilakukan oleh suatu gaya, menghitung fluks suatu medan, dan menghitung komponen suatu vektor pada arah tertentu.
Contoh Soal Dot Product dalam Fisika
Berikut adalah contoh soal dot product yang berhubungan dengan konsep fisika:
Sebuah kotak dengan massa 10 kg didorong dengan gaya 20 N pada sudut 30 derajat terhadap arah horizontal. Berapakah besar kerja yang dilakukan oleh gaya tersebut untuk memindahkan kotak sejauh 5 meter?
Cara Menyelesaikan Soal Dot Product
Untuk menyelesaikan soal ini, kita perlu menggunakan konsep dot product. Kerja yang dilakukan oleh suatu gaya dapat dihitung dengan rumus:
W = F . d
di mana:
- W adalah kerja yang dilakukan
- F adalah gaya yang bekerja
- d adalah perpindahan
Dalam soal ini, gaya F = 20 N dan perpindahan d = 5 meter. Namun, gaya tersebut tidak bekerja searah dengan perpindahan. Oleh karena itu, kita perlu menghitung komponen gaya yang searah dengan perpindahan, yaitu:
Fx = F cos θ = 20 N cos 30° = 17.32 N
Dengan demikian, kerja yang dilakukan oleh gaya tersebut adalah:
W = Fx . d = 17.32 N . 5 m = 86.6 J
Ilustrasi Gambar, Contoh soal dot product
Gambar di bawah ini menunjukkan ilustrasi dari soal di atas:
Gambar tersebut menunjukkan sebuah kotak yang didorong dengan gaya F pada sudut 30 derajat terhadap arah horizontal. Komponen gaya yang searah dengan perpindahan adalah Fx, yang merupakan proyeksi F pada arah horizontal.
Soal Dot Product dengan Aplikasi Geometri
Dot product adalah operasi matematika yang menghasilkan skalar dari dua vektor. Hasil dot product dapat diinterpretasikan sebagai ukuran seberapa “mirip” dua vektor. Konsep ini memiliki aplikasi luas dalam geometri, khususnya dalam menghitung panjang proyeksi satu vektor ke vektor lainnya, serta menghitung sudut antara dua vektor.
Contoh Soal Dot Product dengan Aplikasi Geometri
Perhatikan segitiga ABC dengan titik A(1, 2), B(3, 4), dan C(5, 1). Tentukan panjang proyeksi vektor AB ke vektor AC.
Penjelasan Penyelesaian Soal
Untuk menyelesaikan soal ini, kita dapat menggunakan konsep dot product. Berikut langkah-langkahnya:
- Tentukan vektor AB dan AC:
- AB = B – A = (3, 4) – (1, 2) = (2, 2)
- AC = C – A = (5, 1) – (1, 2) = (4, -1)
- Hitung dot product dari AB dan AC:
- AB · AC = (2, 2) · (4, -1) = (2)(4) + (2)(-1) = 6
- Hitung panjang vektor AC:
- ||AC|| = √(4² + (-1)²) = √17
- Hitung panjang proyeksi AB ke AC:
- Proyeksi AB ke AC = (AB · AC) / ||AC|| = 6 / √17
Ilustrasi Gambar, Contoh soal dot product
Ilustrasi gambar di bawah ini menunjukkan segitiga ABC, vektor AB dan AC, serta proyeksi AB ke AC. Garis putus-putus menunjukkan proyeksi vektor AB ke AC.
Gambar: Ilustrasi segitiga ABC dengan vektor AB, AC, dan proyeksi AB ke AC.
Contoh soal dot product bisa membantu kita memahami konsep perkalian vektor. Misalnya, menghitung proyeksi vektor A ke vektor B. Nah, kalau kita ingin belajar tentang konsep lain, seperti bagaimana membangun website, bisa banget cek contoh soal pemrograman web di https://newcomerscuerna.org/contoh-soal-pemrograman-web/.
Setelah memahami dasar-dasar pemrograman web, kita bisa kembali ke contoh soal dot product untuk mempelajari konsep vektor secara lebih mendalam.
Dari gambar, terlihat bahwa panjang proyeksi AB ke AC adalah jarak dari titik A ke kaki tegak lurus yang ditarik dari titik B ke garis AC. Panjang ini dapat dihitung menggunakan dot product, seperti yang ditunjukkan dalam langkah-langkah di atas.
Soal Dot Product dengan Aplikasi Lainnya
Dot product, atau perkalian skalar, memiliki aplikasi yang luas melampaui fisika dan geometri. Salah satu contohnya adalah dalam bidang komputer grafik, di mana dot product digunakan untuk menghitung pencahayaan dan bayangan.
Pencahayaan dan Bayangan dalam Komputer Grafik
Dalam komputer grafik, dot product digunakan untuk menentukan intensitas cahaya yang mengenai suatu permukaan. Hal ini penting untuk menciptakan efek realistis dalam rendering 3D.
Intensitas cahaya yang mengenai permukaan dipengaruhi oleh:
- Arah cahaya: Arah dari mana cahaya datang.
- Arah normal permukaan: Arah yang tegak lurus terhadap permukaan.
Dot product antara vektor arah cahaya dan vektor arah normal permukaan akan memberikan nilai skalar yang menunjukkan seberapa banyak cahaya mengenai permukaan.
Jika kedua vektor sejajar, maka dot product akan bernilai maksimum, menunjukkan bahwa cahaya mengenai permukaan secara langsung. Sebaliknya, jika kedua vektor tegak lurus, maka dot product akan bernilai nol, menunjukkan bahwa cahaya tidak mengenai permukaan sama sekali.
Contoh Soal
Misalkan sebuah objek dengan permukaan yang memiliki arah normal n = (0, 1, 0) disinari oleh cahaya dengan arah l = (1, 1, 1). Hitunglah intensitas cahaya yang mengenai permukaan tersebut.
Penyelesaian:
n · l = (0, 1, 0) · (1, 1, 1) = (0 * 1) + (1 * 1) + (0 * 1) = 1.
Hasil dot product adalah 1, menunjukkan bahwa cahaya mengenai permukaan secara langsung.
Penutupan Akhir
Contoh soal dot product yang telah kita bahas menunjukkan bagaimana konsep ini diterapkan dalam berbagai bidang, mulai dari fisika hingga geometri. Dengan memahami cara menghitung dan menginterpretasikan hasil dot product, kita dapat membuka pintu untuk pemahaman yang lebih mendalam tentang konsep vektor dan aplikasinya dalam dunia nyata.




