Contoh soal grafik fungsi eksponen dan jawabannya – Pernahkah Anda bertanya-tanya bagaimana bentuk kurva yang menggambarkan pertumbuhan populasi, peluruhan radioaktif, atau bahkan bunga majemuk? Jawabannya terletak pada fungsi eksponen, sebuah fungsi matematika yang mampu menggambarkan perubahan yang cepat dan dramatis. Dalam artikel ini, kita akan menjelajahi dunia grafik fungsi eksponen, mulai dari definisi hingga penerapannya dalam kehidupan sehari-hari.
Kita akan mempelajari cara menggambar grafik fungsi eksponen, menganalisis sifat-sifatnya, dan menyelesaikan berbagai soal yang berkaitan dengan kurva eksponensial. Dengan memahami konsep ini, Anda akan dapat memahami fenomena alam dan sosial yang terjadi di sekitar kita dengan lebih baik.
Pengertian Fungsi Eksponen
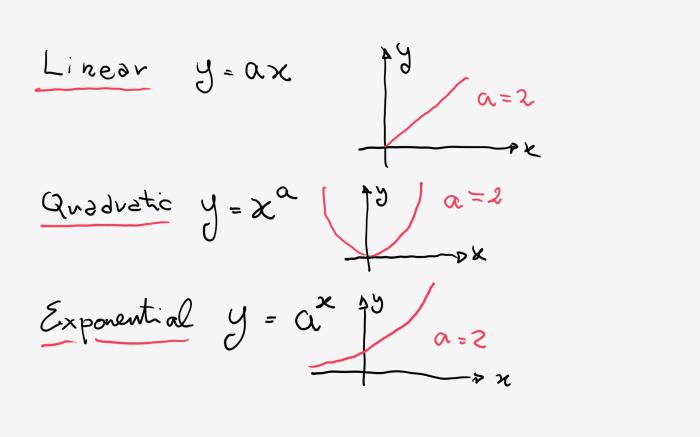
Fungsi eksponen adalah salah satu jenis fungsi matematika yang memiliki bentuk umum y = ax, dengan a adalah bilangan real positif dan x adalah variabel bebas. Dalam fungsi eksponen, variabel x berada di pangkat, sedangkan basisnya adalah bilangan tetap.
Contoh Fungsi Eksponen
Contoh fungsi eksponen sederhana adalah y = 2x. Dalam fungsi ini, basisnya adalah 2 dan variabel x berada di pangkat. Jika kita substitusikan nilai x dengan beberapa bilangan, kita akan mendapatkan nilai y yang berbeda. Misalnya, jika x = 0, maka y = 20 = 1. Jika x = 1, maka y = 21 = 2. Jika x = 2, maka y = 22 = 4. Dan seterusnya.
Karakteristik Fungsi Eksponen
Fungsi eksponen memiliki beberapa karakteristik yang membedakannya dari fungsi lain, seperti fungsi linear dan kuadrat. Berikut adalah beberapa karakteristik fungsi eksponen:
- Grafik fungsi eksponen selalu melengkung, tidak seperti fungsi linear yang berbentuk garis lurus atau fungsi kuadrat yang berbentuk parabola.
- Fungsi eksponen dapat meningkat dengan cepat jika basisnya lebih besar dari 1. Semakin besar basisnya, semakin cepat fungsi tersebut meningkat.
- Fungsi eksponen dapat menurun dengan cepat jika basisnya berada di antara 0 dan 1. Semakin kecil basisnya, semakin cepat fungsi tersebut menurun.
- Fungsi eksponen tidak pernah memotong sumbu x, kecuali jika basisnya adalah 1.
- Fungsi eksponen memiliki asimtot horizontal, yaitu garis yang didekati grafik fungsi saat x mendekati tak terhingga atau negatif tak terhingga.
Perbandingan Fungsi Eksponen dengan Fungsi Linear dan Kuadrat
Berikut tabel yang membandingkan fungsi eksponen dengan fungsi linear dan kuadrat, meliputi persamaan, grafik, dan sifat-sifatnya:
| Fungsi | Persamaan | Grafik | Sifat |
|---|---|---|---|
| Linear | y = mx + c | Garis lurus | Memiliki kemiringan konstan, dapat memotong sumbu x dan y |
| Kuadrat | y = ax2 + bx + c | Parabola | Memiliki titik puncak, dapat memotong sumbu x dan y, simetris terhadap sumbu vertikal |
| Eksponen | y = ax | Melengkung | Meningkat atau menurun dengan cepat, tidak pernah memotong sumbu x (kecuali basisnya 1), memiliki asimtot horizontal |
Pengaruh Karakteristik pada Grafik
Karakteristik fungsi eksponen, seperti basis dan asimtot horizontal, memiliki pengaruh yang signifikan pada bentuk grafiknya.
- Basis: Basis fungsi eksponen menentukan kecepatan pertumbuhan atau penurunan fungsi. Basis yang lebih besar dari 1 akan menghasilkan grafik yang meningkat dengan cepat, sedangkan basis yang berada di antara 0 dan 1 akan menghasilkan grafik yang menurun dengan cepat.
- Asimtot horizontal: Asimtot horizontal menunjukkan nilai yang didekati grafik fungsi saat x mendekati tak terhingga atau negatif tak terhingga. Asimtot horizontal dapat membantu dalam menentukan perilaku fungsi pada nilai x yang sangat besar atau sangat kecil.
Grafik Fungsi Eksponen
Fungsi eksponen memiliki bentuk umum y = ax, di mana a adalah bilangan real positif dan x adalah variabel bebas. Grafik fungsi eksponen memiliki ciri khas yang unik, yaitu bentuknya yang melengkung dan selalu berada di atas sumbu x jika a > 1, atau di bawah sumbu x jika 0 < a < 1. Untuk memahami lebih lanjut tentang grafik fungsi eksponen, mari kita bahas beberapa aspek penting.
Cara Menggambar Grafik Fungsi Eksponen
Menggambar grafik fungsi eksponen dapat dilakukan dengan beberapa langkah mudah. Berikut adalah panduannya:
- Tentukan nilai a dan b: Nilai a menentukan arah lengkung grafik, sedangkan nilai b menentukan titik potong grafik dengan sumbu y.
- Buat tabel nilai: Pilih beberapa nilai x dan hitung nilai y yang bersesuaian dengan fungsi y = ax + b.
- Plot titik-titik pada koordinat kartesius: Titik-titik yang diperoleh dari tabel nilai diplot pada koordinat kartesius.
- Hubungkan titik-titik tersebut dengan kurva halus: Hubungkan titik-titik yang telah diplot dengan kurva halus untuk mendapatkan grafik fungsi eksponen.
Contoh Grafik Fungsi Eksponen
Berikut adalah beberapa contoh grafik fungsi eksponen dengan nilai a dan b yang berbeda:
Grafik Fungsi Eksponen dengan a Positif dan b Positif
Misalnya, kita ingin menggambar grafik fungsi y = 2x + 1. Nilai a adalah 2 (positif) dan nilai b adalah 1 (positif). Kita dapat membuat tabel nilai seperti berikut:
| x | y = 2x + 1 |
|---|---|
| -2 | 1.25 |
| -1 | 1.5 |
| 0 | 2 |
| 1 | 3 |
| 2 | 5 |
Setelah memperoleh titik-titik tersebut, kita dapat memplotnya pada koordinat kartesius dan menghubungkannya dengan kurva halus. Grafik fungsi y = 2x + 1 akan berbentuk kurva yang naik ke atas dan memotong sumbu y di titik (0, 2).
Grafik Fungsi Eksponen dengan a Positif dan b Negatif
Misalnya, kita ingin menggambar grafik fungsi y = 3x – 2. Nilai a adalah 3 (positif) dan nilai b adalah -2 (negatif). Kita dapat membuat tabel nilai seperti berikut:
| x | y = 3x – 2 |
|---|---|
| -2 | -1.89 |
| -1 | -1 |
| 0 | -1 |
| 1 | 1 |
| 2 | 7 |
Setelah memperoleh titik-titik tersebut, kita dapat memplotnya pada koordinat kartesius dan menghubungkannya dengan kurva halus. Grafik fungsi y = 3x – 2 akan berbentuk kurva yang naik ke atas dan memotong sumbu y di titik (0, -1).
Grafik Fungsi Eksponen dengan a Negatif dan b Positif
Misalnya, kita ingin menggambar grafik fungsi y = (-1/2)x + 3. Nilai a adalah -1/2 (negatif) dan nilai b adalah 3 (positif). Kita dapat membuat tabel nilai seperti berikut:
| x | y = (-1/2)x + 3 |
|---|---|
| -2 | 7 |
| -1 | 5 |
| 0 | 4 |
| 1 | 3.5 |
| 2 | 3.25 |
Setelah memperoleh titik-titik tersebut, kita dapat memplotnya pada koordinat kartesius dan menghubungkannya dengan kurva halus. Grafik fungsi y = (-1/2)x + 3 akan berbentuk kurva yang turun ke bawah dan memotong sumbu y di titik (0, 4).
Grafik Fungsi Eksponen dengan a Negatif dan b Negatif
Misalnya, kita ingin menggambar grafik fungsi y = (-1/3)x – 1. Nilai a adalah -1/3 (negatif) dan nilai b adalah -1 (negatif). Kita dapat membuat tabel nilai seperti berikut:
| x | y = (-1/3)x – 1 |
|---|---|
| -2 | -10 |
| -1 | -4 |
| 0 | -2 |
| 1 | -1.67 |
| 2 | -1.11 |
Setelah memperoleh titik-titik tersebut, kita dapat memplotnya pada koordinat kartesius dan menghubungkannya dengan kurva halus. Grafik fungsi y = (-1/3)x – 1 akan berbentuk kurva yang turun ke bawah dan memotong sumbu y di titik (0, -2).
Pengaruh Nilai a dan b terhadap Bentuk Grafik Fungsi Eksponen
Nilai a dan b memiliki pengaruh yang signifikan terhadap bentuk grafik fungsi eksponen:
- Nilai a:
- Jika a > 1, grafik fungsi eksponen akan berbentuk kurva yang naik ke atas dengan cepat.
- Jika 0 < a < 1, grafik fungsi eksponen akan berbentuk kurva yang turun ke bawah dengan cepat.
- Jika a = 1, grafik fungsi eksponen akan berbentuk garis lurus horizontal.
- Nilai b:
- Nilai b menentukan titik potong grafik dengan sumbu y.
- Jika b > 0, grafik fungsi eksponen akan bergeser ke atas.
- Jika b < 0, grafik fungsi eksponen akan bergeser ke bawah.
Sifat-sifat Fungsi Eksponen
Fungsi eksponen memiliki sifat-sifat unik yang membedakannya dari fungsi-fungsi lainnya. Sifat-sifat ini memungkinkan kita untuk memahami dan menganalisis grafik fungsi eksponen dengan lebih baik. Sifat-sifat utama yang akan kita bahas meliputi monoton, asimtot, dan titik potong dengan sumbu.
Monoton
Fungsi eksponen memiliki sifat monoton, yang berarti bahwa fungsi tersebut selalu naik atau selalu turun pada seluruh domainnya. Monotonisitas fungsi eksponen ditentukan oleh nilai basisnya (a) dan eksponennya (x).
- Jika a > 1, maka fungsi eksponen selalu naik (monoton naik).
- Jika 0 < a < 1, maka fungsi eksponen selalu turun (monoton turun).
Asimtot
Asimtot adalah garis yang didekati oleh grafik fungsi ketika x mendekati tak hingga atau minus tak hingga. Fungsi eksponen memiliki asimtot horizontal, yaitu garis horizontal yang didekati oleh grafik fungsi ketika x mendekati tak hingga atau minus tak hingga.
- Jika a > 1, maka asimtot horizontalnya adalah garis y = 0 (sumbu x).
- Jika 0 < a < 1, maka asimtot horizontalnya adalah garis y = 0 (sumbu x).
Titik Potong dengan Sumbu
Titik potong dengan sumbu adalah titik di mana grafik fungsi memotong sumbu x atau sumbu y.
- Titik potong dengan sumbu y: Untuk mencari titik potong dengan sumbu y, kita dapat mensubstitusikan x = 0 ke dalam persamaan fungsi eksponen. Nilai y yang diperoleh adalah titik potong dengan sumbu y.
- Titik potong dengan sumbu x: Untuk mencari titik potong dengan sumbu x, kita dapat mensubstitusikan y = 0 ke dalam persamaan fungsi eksponen. Nilai x yang diperoleh adalah titik potong dengan sumbu x.
Tabel Sifat-Sifat Fungsi Eksponen
| Sifat | Keterangan | Contoh |
|---|---|---|
| Monoton | Fungsi selalu naik atau turun pada seluruh domainnya. | y = 2x (monoton naik) dan y = (1/2)x (monoton turun) |
| Asimtot | Garis yang didekati oleh grafik fungsi ketika x mendekati tak hingga atau minus tak hingga. | y = 2x dan y = (1/2)x memiliki asimtot horizontal y = 0 |
| Titik Potong dengan Sumbu | Titik di mana grafik fungsi memotong sumbu x atau sumbu y. | y = 2x memotong sumbu y di titik (0, 1) dan tidak memotong sumbu x. |
Analisis Grafik Fungsi Eksponen
Sifat-sifat fungsi eksponen dapat digunakan untuk menganalisis grafik fungsi eksponen dengan lebih mudah. Dengan memahami sifat-sifat tersebut, kita dapat menentukan:
- Arah grafik (naik atau turun)
- Asimtot horizontal
- Titik potong dengan sumbu
Informasi ini membantu kita untuk menggambar grafik fungsi eksponen dengan lebih akurat dan memahami perilaku fungsi tersebut.
Soal-soal Grafik Fungsi Eksponen
Setelah mempelajari tentang fungsi eksponen, selanjutnya kita akan membahas beberapa contoh soal yang berhubungan dengan grafik fungsi eksponen. Soal-soal ini akan membantu kamu untuk memahami konsep dan penerapan fungsi eksponen dalam konteks grafis.
Menentukan Persamaan Fungsi Eksponen dari Grafik
Salah satu contoh soal yang sering muncul adalah menentukan persamaan fungsi eksponen dari grafik yang diberikan. Untuk menyelesaikan soal ini, kamu perlu memahami beberapa hal penting. Pertama, bentuk umum fungsi eksponen adalah y = a(b)^x, di mana a dan b adalah konstanta. Kedua, kamu perlu menentukan nilai a dan b dengan menggunakan titik-titik yang terdapat pada grafik. Ketiga, perhatikan bahwa grafik fungsi eksponen selalu melalui titik (0, a).
Menentukan Titik Potong Grafik Fungsi Eksponen dengan Sumbu x dan Sumbu y
Soal lain yang sering dijumpai adalah menentukan titik potong grafik fungsi eksponen dengan sumbu x dan sumbu y. Titik potong dengan sumbu x adalah titik di mana y = 0, sedangkan titik potong dengan sumbu y adalah titik di mana x = 0.
- Untuk menentukan titik potong dengan sumbu x, kamu dapat mensubstitusikan y = 0 ke dalam persamaan fungsi eksponen dan menyelesaikan persamaan tersebut untuk mendapatkan nilai x.
- Untuk menentukan titik potong dengan sumbu y, kamu dapat mensubstitusikan x = 0 ke dalam persamaan fungsi eksponen dan menyelesaikan persamaan tersebut untuk mendapatkan nilai y.
Menentukan Asimtot Horizontal dan Vertikal dari Grafik Fungsi Eksponen
Asimtot adalah garis yang didekati oleh grafik fungsi saat x mendekati tak hingga atau minus tak hingga. Asimtot horizontal dan vertikal dapat membantu kita memahami perilaku grafik fungsi eksponen pada nilai x yang sangat besar atau sangat kecil.
- Asimtot horizontal adalah garis horizontal yang didekati oleh grafik fungsi saat x mendekati tak hingga atau minus tak hingga. Untuk menentukan asimtot horizontal, perhatikan nilai b dalam persamaan fungsi eksponen y = a(b)^x. Jika |b| 1, maka asimtot horizontalnya tidak ada.
- Asimtot vertikal adalah garis vertikal yang didekati oleh grafik fungsi saat x mendekati suatu nilai tertentu. Untuk menentukan asimtot vertikal, perhatikan nilai a dalam persamaan fungsi eksponen y = a(b)^x. Jika a = 0, maka asimtot vertikalnya adalah garis x = 0. Jika a ≠ 0, maka asimtot vertikalnya tidak ada.
Penerapan Fungsi Eksponen
Fungsi eksponen memiliki peran penting dalam berbagai bidang kehidupan, baik di dunia sains, ekonomi, maupun teknologi. Penerapannya dalam berbagai fenomena alam dan sistem manusia membantu kita memahami dan memprediksi perilaku berbagai proses yang terjadi di sekitar kita.
Pertumbuhan Penduduk
Fungsi eksponen dapat digunakan untuk memodelkan pertumbuhan penduduk. Pertumbuhan penduduk biasanya tidak linear, tetapi cenderung meningkat secara eksponensial. Hal ini terjadi karena semakin banyak penduduk, semakin banyak pula kelahiran yang terjadi.
Rumus pertumbuhan penduduk: P(t) = P0ert
Dimana:
* P(t) adalah populasi pada waktu t
* P0 adalah populasi awal
* r adalah laju pertumbuhan penduduk
* t adalah waktu
Sebagai contoh, jika populasi awal suatu negara adalah 10 juta jiwa dan laju pertumbuhannya adalah 2% per tahun, maka populasi setelah 10 tahun dapat dihitung menggunakan rumus tersebut.
Peluruhan Radioaktif, Contoh soal grafik fungsi eksponen dan jawabannya
Peluruhan radioaktif adalah proses di mana inti atom tidak stabil melepaskan energi dan partikel untuk menjadi lebih stabil. Proses ini mengikuti model eksponensial, di mana jumlah bahan radioaktif yang tersisa berkurang secara eksponensial seiring waktu.
Rumus peluruhan radioaktif: N(t) = N0e-λt
Dimana:
* N(t) adalah jumlah bahan radioaktif pada waktu t
* N0 adalah jumlah bahan radioaktif awal
* λ adalah konstanta peluruhan
* t adalah waktu
Sebagai contoh, jika sebuah sampel radioaktif memiliki setengah umur 10 tahun, maka setelah 10 tahun jumlah bahan radioaktif akan berkurang menjadi setengahnya. Setelah 20 tahun, jumlahnya akan berkurang menjadi seperempatnya, dan seterusnya.
Bunga Majemuk
Bunga majemuk adalah bunga yang dihitung atas pokok pinjaman dan bunga yang telah terkumpul sebelumnya. Model pertumbuhan bunga majemuk mengikuti fungsi eksponensial. Semakin lama waktu, semakin besar pula jumlah bunga yang terkumpul.
Rumus bunga majemuk: A = P(1 + r/n)nt
Dimana:
* A adalah jumlah total setelah t tahun
* P adalah pokok pinjaman
* r adalah suku bunga tahunan
* n adalah jumlah kali bunga dihitung dalam setahun
* t adalah waktu dalam tahun
Sebagai contoh, jika Anda menabung Rp10.000.000 dengan suku bunga 5% per tahun, dan bunga dihitung setiap bulan, maka setelah 5 tahun, jumlah tabungan Anda akan menjadi sekitar Rp12.833.595.
Tabel Rangkuman
Berikut tabel yang merangkum contoh-contoh penerapan fungsi eksponen dan persamaan yang digunakan:
| Penerapan | Persamaan |
|---|---|
| Pertumbuhan Penduduk | P(t) = P0ert |
| Peluruhan Radioaktif | N(t) = N0e-λt |
| Bunga Majemuk | A = P(1 + r/n)nt |
Pembahasan Soal Grafik Fungsi Eksponen: Contoh Soal Grafik Fungsi Eksponen Dan Jawabannya
Grafik fungsi eksponen adalah representasi visual dari hubungan antara input dan output dalam fungsi eksponen. Memahami cara menggambar dan menganalisis grafik fungsi eksponen sangat penting untuk memahami perilaku fungsi eksponen, yang memiliki banyak aplikasi dalam berbagai bidang seperti pertumbuhan populasi, peluruhan radioaktif, dan pertumbuhan investasi.
Contoh Soal Grafik Fungsi Eksponen dan Jawabannya
Berikut adalah contoh soal grafik fungsi eksponen dan langkah-langkah penyelesaiannya:
Soal: Gambarlah grafik fungsi eksponen y = 2x dan tentukan domain dan range-nya.
Penyelesaian:
- Buat tabel nilai. Pilih beberapa nilai x dan hitung nilai y yang sesuai dengan fungsi y = 2x.
- Plot titik-titik pada grafik. Gunakan tabel nilai untuk memplot titik-titik pada grafik. Misalnya, titik (-2, 1/4), (-1, 1/2), (0, 1), (1, 2), dan (2, 4).
- Hubungkan titik-titik dengan kurva mulus. Hubungkan titik-titik yang telah diplot dengan kurva mulus. Kurva ini akan menunjukkan grafik fungsi y = 2x.
- Tentukan domain dan range. Domain fungsi eksponen y = 2x adalah semua bilangan real, karena x dapat mengambil nilai apa pun. Range fungsi ini adalah semua bilangan real positif, karena y selalu positif untuk setiap nilai x.
| x | y = 2x |
|---|---|
| -2 | 2-2 = 1/4 |
| -1 | 2-1 = 1/2 |
| 0 | 20 = 1 |
| 1 | 21 = 2 |
| 2 | 22 = 4 |
Konsep dan Prinsip yang Digunakan
Konsep dan prinsip yang digunakan dalam menyelesaikan soal-soal grafik fungsi eksponen meliputi:
- Definisi fungsi eksponen: Fungsi eksponen adalah fungsi yang memiliki bentuk y = ax, di mana a adalah basis dan x adalah eksponen.
- Sifat-sifat eksponen: Sifat-sifat eksponen digunakan untuk menghitung nilai fungsi eksponen untuk berbagai nilai x.
- Grafik fungsi eksponen: Grafik fungsi eksponen adalah kurva yang menunjukkan hubungan antara input (x) dan output (y) dalam fungsi eksponen.
- Domain dan range: Domain adalah himpunan semua nilai x yang memungkinkan dalam fungsi, sedangkan range adalah himpunan semua nilai y yang dihasilkan oleh fungsi.
Kesulitan yang Mungkin Dihadapi Siswa
Siswa mungkin menghadapi kesulitan dalam memahami konsep dan menyelesaikan soal-soal grafik fungsi eksponen, terutama dalam:
- Memahami sifat-sifat eksponen: Siswa mungkin kesulitan memahami dan menerapkan sifat-sifat eksponen, seperti am * an = am+n dan am / an = am-n.
- Menggambar grafik fungsi eksponen: Siswa mungkin kesulitan menentukan titik-titik yang tepat untuk diplot pada grafik dan menghubungkan titik-titik tersebut dengan kurva yang benar.
- Menganalisis grafik fungsi eksponen: Siswa mungkin kesulitan menentukan domain dan range fungsi eksponen dari grafiknya.
Strategi Menyelesaikan Soal Grafik Fungsi Eksponen
Menjelajahi dunia fungsi eksponen bisa jadi menyenangkan, tapi tentu saja ada tantangannya. Grafik fungsi eksponen bisa terlihat rumit, tapi tenang, ada beberapa strategi jitu yang bisa kamu gunakan untuk menguasainya. Dengan memahami dasar-dasarnya dan menerapkan langkah-langkah sistematis, kamu bisa memecahkan soal-soal grafik fungsi eksponen dengan cepat dan tepat.
Memahami Konsep Dasar
Sebelum kita terjun ke strategi, penting untuk memahami konsep dasar fungsi eksponen. Fungsi eksponen memiliki bentuk umum y = a^x, dimana a adalah basis eksponen (a > 0 dan a ≠ 1) dan x adalah eksponen. Grafik fungsi eksponen memiliki ciri khas yang unik, yaitu selalu meningkat atau menurun secara eksponensial.
- Jika a > 1, grafik fungsi akan meningkat secara eksponensial, artinya semakin besar nilai x, semakin besar nilai y.
- Jika 0 < a < 1, grafik fungsi akan menurun secara eksponensial, artinya semakin besar nilai x, semakin kecil nilai y.
Strategi Menyelesaikan Soal Grafik Fungsi Eksponen
Nah, sekarang kita masuk ke strategi jitu untuk menyelesaikan soal-soal grafik fungsi eksponen. Berikut beberapa langkah yang bisa kamu ikuti:
- Identifikasi bentuk fungsi eksponen: Tentukan bentuk umum fungsi eksponen yang diberikan, yaitu y = a^x. Pastikan kamu tahu nilai a (basis eksponen) dan x (eksponen).
- Tentukan titik potong dengan sumbu y: Titik potong dengan sumbu y adalah titik di mana x = 0. Substitusikan x = 0 ke dalam persamaan fungsi eksponen untuk mendapatkan nilai y. Titik potong ini akan menjadi titik awal grafik.
- Tentukan titik potong dengan sumbu x: Titik potong dengan sumbu x adalah titik di mana y = 0. Substitusikan y = 0 ke dalam persamaan fungsi eksponen dan selesaikan persamaan untuk mendapatkan nilai x. Titik potong ini akan membantu kamu menentukan arah grafik.
- Tentukan perilaku grafik: Perhatikan nilai a (basis eksponen). Jika a > 1, grafik akan meningkat secara eksponensial. Jika 0 < a < 1, grafik akan menurun secara eksponensial.
- Buat tabel nilai: Buat tabel nilai dengan beberapa nilai x dan hitung nilai y yang sesuai. Ini akan membantu kamu mendapatkan beberapa titik yang bisa kamu plot pada grafik.
- Plot titik-titik pada grafik: Plot titik-titik yang telah kamu dapatkan pada tabel nilai di atas kertas grafik.
- Hubungkan titik-titik dengan garis halus: Hubungkan titik-titik yang telah kamu plot dengan garis halus untuk mendapatkan grafik fungsi eksponen.
Contoh Soal dan Solusi
Mari kita lihat contoh soal dan solusinya untuk memperjelas strategi ini.
Soal: Gambarlah grafik fungsi eksponen y = 2^x.
Solusi:
- Identifikasi bentuk fungsi eksponen: Fungsi eksponen yang diberikan adalah y = 2^x, di mana a = 2 (basis eksponen) dan x adalah eksponen.
- Tentukan titik potong dengan sumbu y: Substitusikan x = 0 ke dalam persamaan fungsi eksponen: y = 2^0 = 1. Titik potong dengan sumbu y adalah (0, 1).
- Tentukan titik potong dengan sumbu x: Substitusikan y = 0 ke dalam persamaan fungsi eksponen: 0 = 2^x. Tidak ada nilai x yang memenuhi persamaan ini, sehingga grafik tidak memotong sumbu x.
- Tentukan perilaku grafik: Karena a = 2 > 1, grafik akan meningkat secara eksponensial.
- Buat tabel nilai:
- Plot titik-titik pada grafik: Plot titik-titik ( -2, 1/4), (-1, 1/2), (0, 1), (1, 2), dan (2, 4) pada kertas grafik.
- Hubungkan titik-titik dengan garis halus: Hubungkan titik-titik yang telah kamu plot dengan garis halus untuk mendapatkan grafik fungsi eksponen y = 2^x. Grafik akan meningkat secara eksponensial dan tidak akan memotong sumbu x.
| x | y = 2^x |
|---|---|
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
Dengan mengikuti langkah-langkah ini, kamu bisa menyelesaikan soal-soal grafik fungsi eksponen dengan mudah dan tepat.
Latihan Soal Grafik Fungsi Eksponen
Setelah memahami konsep dasar fungsi eksponen dan cara menggambar grafiknya, sekarang saatnya untuk mengasah kemampuanmu dengan latihan soal. Berikut ini beberapa contoh soal grafik fungsi eksponen dengan berbagai tingkat kesulitan, lengkap dengan kunci jawaban dan pembahasannya.
Soal Latihan
Untuk mempermudah pemahaman, soal-soal latihan dibagi menjadi beberapa tingkatan kesulitan, yaitu:
- Tingkat Mudah: Soal-soal ini dirancang untuk menguji pemahaman dasar tentang fungsi eksponen dan grafiknya.
- Tingkat Sedang: Soal-soal ini menguji kemampuanmu dalam mengaplikasikan konsep fungsi eksponen dan menggambar grafiknya.
- Tingkat Sulit: Soal-soal ini menguji kemampuanmu dalam menyelesaikan masalah yang kompleks dan melibatkan analisis yang lebih mendalam.
Contoh Soal Tingkat Mudah
Berikut adalah contoh soal tingkat mudah:
- Gambarlah grafik fungsi eksponen y = 2x.
- Tentukan persamaan fungsi eksponen yang grafiknya melalui titik (0, 1) dan (1, 2).
Kunci Jawaban dan Pembahasan
Soal 1
Untuk menggambar grafik fungsi y = 2x, kita dapat membuat tabel nilai:
| x | y = 2x |
|---|---|
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
Kemudian, plot titik-titik tersebut pada bidang kartesius dan hubungkan titik-titik tersebut dengan kurva mulus. Grafik fungsi y = 2x akan berbentuk kurva yang selalu naik dan tidak pernah memotong sumbu x.
Soal 2
Persamaan fungsi eksponen umum adalah y = ax. Karena grafik fungsi melalui titik (0, 1), maka nilai a = 1. Karena grafik fungsi juga melalui titik (1, 2), maka:
2 = 11
Jadi, persamaan fungsi eksponen yang grafiknya melalui titik (0, 1) dan (1, 2) adalah y = 2x.
Contoh Soal Tingkat Sedang
Berikut adalah contoh soal tingkat sedang:
- Tentukan persamaan fungsi eksponen yang grafiknya melalui titik (1, 3) dan (2, 9).
- Tentukan persamaan asimtot horizontal dari fungsi eksponen y = 3x + 2.
Kunci Jawaban dan Pembahasan
Soal 1
Persamaan fungsi eksponen umum adalah y = ax. Karena grafik fungsi melalui titik (1, 3), maka:
3 = a1
Sehingga, a = 3. Karena grafik fungsi juga melalui titik (2, 9), maka:
9 = 32
Jadi, persamaan fungsi eksponen yang grafiknya melalui titik (1, 3) dan (2, 9) adalah y = 3x.
Soal 2
Asimtot horizontal dari fungsi eksponen y = ax + c adalah y = c. Jadi, asimtot horizontal dari fungsi eksponen y = 3x + 2 adalah y = 2.
Contoh Soal Tingkat Sulit
Berikut adalah contoh soal tingkat sulit:
- Tentukan persamaan fungsi eksponen yang grafiknya melalui titik (0, 2) dan (1, 6) serta memotong sumbu y di titik (0, 2).
- Tentukan domain dan range dari fungsi eksponen y = 2-x + 1.
Kunci Jawaban dan Pembahasan
Soal 1
Persamaan fungsi eksponen umum adalah y = ax + c. Karena grafik fungsi memotong sumbu y di titik (0, 2), maka c = 2. Karena grafik fungsi juga melalui titik (1, 6), maka:
6 = a1 + 2
Sehingga, a = 4. Jadi, persamaan fungsi eksponen yang grafiknya melalui titik (0, 2) dan (1, 6) serta memotong sumbu y di titik (0, 2) adalah y = 4x + 2.
Soal 2
Domain dari fungsi eksponen y = 2-x + 1 adalah semua bilangan real, yaitu (-∞, ∞). Range dari fungsi eksponen y = 2-x + 1 adalah (1, ∞), karena nilai 2-x selalu positif dan nilai minimumnya adalah 0, sehingga nilai minimum dari fungsi tersebut adalah 1.
Mencari contoh soal grafik fungsi eksponen dan jawabannya? Nah, selain itu, kamu juga bisa mempelajari tentang contoh soal ogive yang membahas tentang penyajian data statistik dalam bentuk kurva. Keduanya merupakan topik penting dalam matematika yang perlu dipahami. Meskipun berbeda, pemahaman tentang kedua topik ini akan membantu kamu dalam menyelesaikan berbagai permasalahan terkait fungsi dan data.
Jadi, yuk, pelajari contoh soal grafik fungsi eksponen dan jawabannya, serta contoh soal ogive, agar kamu lebih siap menghadapi tantangan matematika!
Tips dan Saran
Berikut adalah beberapa tips dan saran untuk siswa yang mengalami kesulitan dalam mengerjakan soal-soal latihan grafik fungsi eksponen:
- Pahami konsep dasar fungsi eksponen dan grafiknya.
- Latih menggambar grafik fungsi eksponen dengan berbagai nilai a dan c.
- Pelajari sifat-sifat fungsi eksponen, seperti asimtot horizontal dan domain.
- Jangan takut untuk bertanya kepada guru atau teman jika mengalami kesulitan.
- Latih mengerjakan soal-soal latihan secara rutin untuk meningkatkan kemampuanmu.
Contoh Soal Grafik Fungsi Eksponen dan Jawabannya
Fungsi eksponen merupakan fungsi yang melibatkan variabel berpangkat. Grafik fungsi eksponen memiliki bentuk yang khas, yaitu berbentuk kurva yang naik atau turun dengan cepat. Untuk memahami fungsi eksponen lebih lanjut, mari kita pelajari beberapa contoh soal dan jawabannya.
Contoh Soal dan Jawaban Grafik Fungsi Eksponen
Berikut ini adalah tabel yang berisi contoh soal grafik fungsi eksponen dan jawabannya, disertai dengan pembahasan yang lengkap:
| No. | Persamaan Fungsi | Grafik | Langkah Penyelesaian |
|---|---|---|---|
| 1 | y = 2x |
Grafik fungsi y = 2x berbentuk kurva yang naik dengan cepat, melintasi sumbu y di titik (0, 1) dan tidak pernah memotong sumbu x. |
|
| 2 | y = (1/2)x |
Grafik fungsi y = (1/2)x berbentuk kurva yang turun dengan cepat, melintasi sumbu y di titik (0, 1) dan tidak pernah memotong sumbu x. |
|
| 3 | y = 3x – 1 |
Grafik fungsi y = 3x – 1 berbentuk kurva yang naik dengan cepat, melintasi sumbu y di titik (0, 1/3) dan tidak pernah memotong sumbu x. |
|
Soal Grafik Fungsi Eksponen dengan Variasi
Selain soal-soal standar, soal grafik fungsi eksponen dapat disajikan dengan variasi yang lebih menarik dan menantang. Variasi ini dapat berupa soal cerita, soal gambar, atau kombinasi keduanya. Kemampuan untuk memahami dan menyelesaikan soal-soal dengan variasi tersebut akan membantu kita dalam mengasah kemampuan berpikir kritis dan memecahkan masalah.
Soal Cerita
Soal cerita melibatkan situasi nyata yang dimodelkan dengan fungsi eksponen. Kita perlu memahami konteks cerita dan menerjemahkannya ke dalam persamaan matematika.
- Misalnya, sebuah bakteri berkembang biak dengan kecepatan yang eksponensial. Jika jumlah bakteri awal adalah 100 dan jumlahnya berlipat ganda setiap 2 jam, berapa banyak bakteri setelah 8 jam?
- Kita dapat memodelkan pertumbuhan bakteri dengan fungsi eksponen: y = 100 * 2^(t/2), dengan y adalah jumlah bakteri dan t adalah waktu dalam jam. Untuk mencari jumlah bakteri setelah 8 jam, kita substitusikan t = 8 ke dalam persamaan dan mendapatkan y = 100 * 2^(8/2) = 1600 bakteri.
Soal Gambar
Soal gambar melibatkan interpretasi grafik fungsi eksponen. Kita perlu menganalisis bentuk grafik dan menentukan persamaan fungsi yang sesuai.
- Misalnya, diberikan grafik fungsi eksponen dengan titik potong sumbu y di (0, 2) dan melalui titik (1, 4). Tentukan persamaan fungsi tersebut.
- Kita tahu bahwa persamaan umum fungsi eksponen adalah y = a * b^x. Dari titik potong sumbu y, kita dapat menentukan a = 2. Dari titik (1, 4), kita dapat menentukan b = 2. Jadi, persamaan fungsi tersebut adalah y = 2 * 2^x.
Soal Kombinasi
Soal kombinasi menggabungkan elemen soal cerita dan soal gambar. Kita perlu memahami konteks cerita, menganalisis grafik, dan menentukan persamaan fungsi yang sesuai.
- Misalnya, diberikan grafik pertumbuhan populasi suatu hewan dengan waktu. Grafik menunjukkan bahwa populasi hewan tersebut meningkat secara eksponensial. Pertanyaan: tentukan persamaan fungsi yang memodelkan pertumbuhan populasi hewan tersebut dan prediksi populasi hewan tersebut pada tahun ke-10.
- Kita dapat menentukan persamaan fungsi berdasarkan titik-titik pada grafik dan menentukan persamaan fungsi yang sesuai. Selanjutnya, kita dapat menggunakan persamaan tersebut untuk memprediksi populasi hewan tersebut pada tahun ke-10.
Ringkasan Terakhir
Melalui contoh soal dan pembahasan yang lengkap, artikel ini telah membawa Anda untuk memahami karakteristik dan perilaku grafik fungsi eksponen. Dengan pengetahuan ini, Anda dapat menganalisis berbagai fenomena yang diwakili oleh fungsi eksponen, seperti pertumbuhan penduduk, peluruhan radioaktif, dan bunga majemuk. Semoga artikel ini bermanfaat dan membuka wawasan baru tentang dunia matematika yang menakjubkan.





