Contoh soal grafik trigonometri – Pernahkah Anda melihat gelombang laut yang berirama naik turun? Atau mungkin getaran senar gitar yang menghasilkan melodi indah? Di balik keindahan tersebut, terdapat konsep matematika yang menakjubkan: grafik trigonometri. Grafik trigonometri adalah visualisasi dari fungsi trigonometri seperti sinus, cosinus, dan tangen, yang menggambarkan pola periodik dan siklus dalam berbagai fenomena alam dan kehidupan sehari-hari.
Dalam artikel ini, kita akan menjelajahi dunia grafik trigonometri, mulai dari pengertian dasar hingga penerapannya dalam berbagai bidang. Anda akan menemukan contoh soal dan pembahasan yang akan membantu Anda memahami konsep ini dengan lebih baik. Siap untuk menyelami dunia gelombang matematika?
Pengertian Grafik Trigonometri
Grafik trigonometri adalah representasi visual dari fungsi trigonometri, seperti sinus (sin), cosinus (cos), dan tangen (tan). Grafik ini menunjukkan hubungan antara sudut dan nilai fungsi trigonometri pada lingkaran satuan.
Fungsi Trigonometri Dasar dan Grafiknya
Berikut adalah beberapa fungsi trigonometri dasar beserta grafiknya:
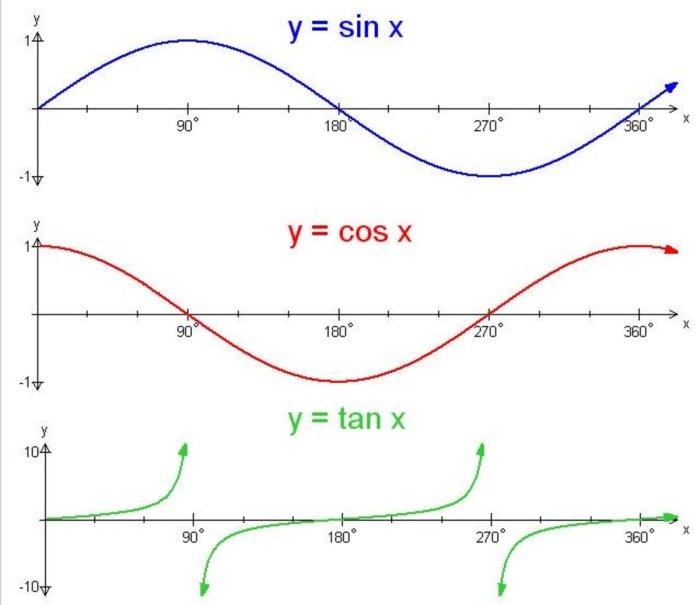
- Sinus (sin): Grafik sinus berbentuk gelombang yang berulang dengan amplitudo 1 dan periode 2π. Grafik ini dimulai dari titik (0, 0) dan mencapai puncak pada (π/2, 1), lalu kembali ke titik (π, 0), mencapai titik terendah pada (3π/2, -1), dan kembali ke titik (2π, 0).
- Cosinus (cos): Grafik cosinus juga berbentuk gelombang yang berulang dengan amplitudo 1 dan periode 2π. Namun, grafik ini dimulai dari titik (0, 1), mencapai titik terendah pada (π, -1), dan kembali ke titik (2π, 1).
- Tangen (tan): Grafik tangen memiliki bentuk yang berbeda dari sinus dan cosinus. Grafik ini memiliki asimtot vertikal pada x = (π/2) + kπ, di mana k adalah bilangan bulat. Grafik ini juga berulang dengan periode π.
Hubungan antara Nilai Fungsi Trigonometri dengan Titik-titik pada Lingkaran Satuan
Nilai fungsi trigonometri dapat dihubungkan dengan titik-titik pada lingkaran satuan. Lingkaran satuan adalah lingkaran dengan jari-jari 1 yang berpusat di titik (0, 0) pada bidang koordinat. Setiap titik pada lingkaran satuan dapat diwakili oleh koordinat (x, y), di mana x adalah nilai cosinus dan y adalah nilai sinus dari sudut yang dibentuk oleh garis yang menghubungkan titik tersebut dengan titik pusat lingkaran satuan.
Misalnya, titik (1/2, √3/2) pada lingkaran satuan mewakili sudut 60°. Nilai cosinus dari sudut 60° adalah 1/2, sedangkan nilai sinusnya adalah √3/2.
Grafik Fungsi Sinus dan Cosinus: Contoh Soal Grafik Trigonometri
Fungsi sinus dan cosinus adalah dua fungsi trigonometri yang sangat penting dalam matematika. Fungsi-fungsi ini memiliki banyak aplikasi dalam berbagai bidang, seperti fisika, teknik, dan ilmu komputer. Grafik fungsi sinus dan cosinus memberikan representasi visual dari perilaku fungsi tersebut, yang membantu kita memahami sifat-sifatnya dengan lebih baik.
Ciri-ciri Grafik Fungsi Sinus dan Cosinus
Grafik fungsi sinus dan cosinus memiliki beberapa ciri khas yang membedakannya dari fungsi trigonometri lainnya. Berikut adalah beberapa ciri-ciri tersebut:
- Periodik: Grafik fungsi sinus dan cosinus berulang secara periodik. Artinya, bentuk grafiknya akan sama untuk setiap interval tertentu. Periode fungsi sinus dan cosinus adalah 360° atau 2π radian.
- Amplitudo: Amplitudo grafik fungsi sinus dan cosinus adalah jarak maksimum dari garis tengah ke titik tertinggi atau terendah pada grafik. Amplitudo fungsi sinus dan cosinus adalah 1.
- Garis Tengah: Garis tengah grafik fungsi sinus dan cosinus adalah garis horizontal yang membagi grafik menjadi dua bagian yang simetris. Garis tengah fungsi sinus dan cosinus adalah sumbu x.
- Puncak dan Lembah: Titik tertinggi pada grafik fungsi sinus dan cosinus disebut puncak, sedangkan titik terendah disebut lembah. Puncak dan lembah fungsi sinus dan cosinus terletak pada nilai 1 dan -1.
- Titik Potong Sumbu: Grafik fungsi sinus dan cosinus memotong sumbu x pada titik-titik tertentu. Titik potong sumbu x fungsi sinus dan cosinus terletak pada kelipatan 180° atau π radian.
Tabel Nilai Sinus dan Cosinus
Berikut adalah tabel yang menunjukkan hubungan antara sudut, nilai sinus, dan nilai cosinus untuk beberapa sudut istimewa:
| Sudut (°) | Sudut (radian) | Sinus | Cosinus |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | π/6 | 1/2 | √3/2 |
| 45° | π/4 | √2/2 | √2/2 |
| 60° | π/3 | √3/2 | 1/2 |
| 90° | π/2 | 1 | 0 |
| 180° | π | 0 | -1 |
| 270° | 3π/2 | -1 | 0 |
| 360° | 2π | 0 | 1 |
Grafik Fungsi Sinus dan Cosinus pada Rentang 0° hingga 360°
Berikut adalah gambaran grafik fungsi sinus dan cosinus pada rentang 0° hingga 360°:
Grafik Fungsi Sinus:
Grafik fungsi sinus dimulai dari titik (0, 0), kemudian naik ke puncak pada sudut 90°, turun kembali ke titik (180°, 0), turun lebih lanjut ke lembah pada sudut 270°, dan akhirnya kembali ke titik (360°, 0). Grafik ini berulang secara periodik dengan periode 360°.
Grafik Fungsi Cosinus:
Grafik fungsi cosinus dimulai dari titik (0, 1), kemudian turun ke titik (90°, 0), turun lebih lanjut ke lembah pada sudut 180°, naik kembali ke titik (270°, 0), dan akhirnya kembali ke titik (360°, 1). Grafik ini juga berulang secara periodik dengan periode 360°.
Grafik Fungsi Tangent
Fungsi tangent merupakan salah satu fungsi trigonometri yang memiliki ciri khas dan sifat unik dalam grafiknya. Grafik fungsi tangent memiliki bentuk yang berbeda dengan grafik fungsi sinus dan cosinus, dan memiliki beberapa ciri khas yang perlu dipahami.
Ciri-ciri Grafik Fungsi Tangent
Berikut beberapa ciri khas yang membedakan grafik fungsi tangent dengan fungsi trigonometri lainnya:
- Grafik fungsi tangent memiliki bentuk yang mirip dengan garis lurus, tetapi dengan bentuk lengkungan yang tajam.
- Grafik fungsi tangent memiliki asimtot vertikal, yaitu garis vertikal yang didekati oleh grafik fungsi tangent tetapi tidak pernah disentuh.
- Grafik fungsi tangent memiliki periode π, artinya bentuk grafik tersebut akan berulang setiap π radian atau 180 derajat.
- Grafik fungsi tangent memiliki titik potong dengan sumbu y di titik (0, 0), dan tidak memiliki titik potong dengan sumbu x.
Hubungan Sudut dan Nilai Tangent
Untuk memahami bentuk grafik fungsi tangent, penting untuk mengetahui hubungan antara sudut dan nilai tangent untuk beberapa sudut istimewa. Berikut tabel yang menunjukkan hubungan tersebut:
| Sudut (°) | Sudut (radian) | Nilai Tangent |
|---|---|---|
| 0° | 0 | 0 |
| 30° | π/6 | √3/3 |
| 45° | π/4 | 1 |
| 60° | π/3 | √3 |
| 90° | π/2 | Tidak terdefinisi |
| 120° | 2π/3 | -√3 |
| 135° | 3π/4 | -1 |
| 150° | 5π/6 | -√3/3 |
| 180° | π | 0 |
| 210° | 7π/6 | √3/3 |
| 225° | 5π/4 | 1 |
| 240° | 4π/3 | √3 |
| 270° | 3π/2 | Tidak terdefinisi |
| 300° | 5π/3 | -√3 |
| 315° | 7π/4 | -1 |
| 330° | 11π/6 | -√3/3 |
| 360° | 2π | 0 |
Grafik Fungsi Tangent pada Rentang 0° hingga 360°
Grafik fungsi tangent pada rentang 0° hingga 360° dapat digambarkan dengan menggunakan tabel hubungan sudut dan nilai tangent di atas. Grafik ini akan menunjukkan bentuk lengkungan yang tajam dan asimtot vertikal yang terjadi pada sudut 90° dan 270°. Grafik tersebut juga akan menunjukkan bahwa fungsi tangent memiliki periode π, artinya bentuk grafik tersebut akan berulang setiap 180 derajat.
Transformasi Grafik Trigonometri
Transformasi grafik fungsi trigonometri adalah proses mengubah bentuk, posisi, atau orientasi grafik fungsi trigonometri dasar. Transformasi ini dilakukan dengan mengubah amplitudo, periode, pergeseran horizontal, dan pergeseran vertikal. Memahami transformasi ini memungkinkan kita untuk menganalisis dan memahami sifat fungsi trigonometri dengan lebih baik, serta memprediksi dan menggambar grafiknya dengan lebih mudah.
Pengaruh Perubahan Amplitudo, Periode, dan Pergeseran
Perubahan amplitudo, periode, dan pergeseran memengaruhi grafik fungsi trigonometri dengan cara berikut:
- Amplitudo: Amplitudo adalah jarak dari garis tengah grafik ke titik tertinggi atau terendah. Mengubah amplitudo akan memengaruhi ketinggian grafik. Jika amplitudo diperbesar, grafik akan lebih tinggi, dan jika amplitudo diperkecil, grafik akan lebih rendah.
- Periode: Periode adalah jarak horizontal yang dibutuhkan grafik untuk menyelesaikan satu siklus lengkap. Mengubah periode akan memengaruhi lebar grafik. Jika periode diperkecil, grafik akan lebih sempit, dan jika periode diperbesar, grafik akan lebih lebar.
- Pergeseran Horizontal: Pergeseran horizontal adalah pergeseran grafik ke kanan atau kiri. Pergeseran ini terjadi ketika kita menambahkan atau mengurangi suatu konstanta dari variabel sudut dalam fungsi trigonometri. Jika konstanta positif, grafik akan bergeser ke kiri, dan jika konstanta negatif, grafik akan bergeser ke kanan.
- Pergeseran Vertikal: Pergeseran vertikal adalah pergeseran grafik ke atas atau ke bawah. Pergeseran ini terjadi ketika kita menambahkan atau mengurangi suatu konstanta dari fungsi trigonometri. Jika konstanta positif, grafik akan bergeser ke atas, dan jika konstanta negatif, grafik akan bergeser ke bawah.
Contoh Fungsi Trigonometri dan Transformasinya
Berikut adalah contoh fungsi trigonometri dan transformasinya beserta grafiknya:
| Fungsi Asli | Transformasi | Persamaan Baru | Grafik |
|---|---|---|---|
| y = sin(x) | Amplitudo diperbesar menjadi 2 | y = 2sin(x) | [Ilustrasi: Grafik y = sin(x) dan y = 2sin(x) dengan amplitudo y = 2sin(x) dua kali lebih tinggi dari y = sin(x)] |
| y = sin(x) | Periode diperkecil menjadi π | y = sin(2x) | [Ilustrasi: Grafik y = sin(x) dan y = sin(2x) dengan periode y = sin(2x) setengah dari y = sin(x)] |
| y = sin(x) | Pergeseran horizontal ke kanan π/2 | y = sin(x – π/2) | [Ilustrasi: Grafik y = sin(x) dan y = sin(x – π/2) dengan y = sin(x – π/2) bergeser ke kanan π/2] |
| y = sin(x) | Pergeseran vertikal ke atas 1 | y = sin(x) + 1 | [Ilustrasi: Grafik y = sin(x) dan y = sin(x) + 1 dengan y = sin(x) + 1 bergeser ke atas 1] |
Menentukan Persamaan Grafik Fungsi Trigonometri yang Telah Mengalami Transformasi
Untuk menentukan persamaan grafik fungsi trigonometri yang telah mengalami transformasi, kita perlu memperhatikan perubahan yang terjadi pada grafik. Berikut adalah langkah-langkah yang dapat kita gunakan:
- Tentukan jenis fungsi trigonometri: Apakah grafik merupakan grafik sinus, kosinus, tangen, atau fungsi trigonometri lainnya?
- Tentukan amplitudo: Amplitudo adalah jarak dari garis tengah grafik ke titik tertinggi atau terendah.
- Tentukan periode: Periode adalah jarak horizontal yang dibutuhkan grafik untuk menyelesaikan satu siklus lengkap.
- Tentukan pergeseran horizontal: Pergeseran horizontal adalah pergeseran grafik ke kanan atau kiri.
- Tentukan pergeseran vertikal: Pergeseran vertikal adalah pergeseran grafik ke atas atau ke bawah.
- Tulis persamaan fungsi trigonometri: Setelah menentukan semua informasi di atas, kita dapat menulis persamaan fungsi trigonometri yang telah mengalami transformasi.
Contohnya, jika grafik fungsi trigonometri memiliki amplitudo 3, periode 2π, pergeseran horizontal π/2 ke kanan, dan pergeseran vertikal 1 ke atas, maka persamaannya adalah:
y = 3sin(x – π/2) + 1
Penerapan Grafik Trigonometri
Grafik trigonometri bukan hanya sekadar gambar matematika yang rumit. Grafik ini memiliki aplikasi luas di berbagai bidang kehidupan, dari yang sederhana hingga yang kompleks. Melalui grafik trigonometri, kita dapat memodelkan dan memahami fenomena periodik, seperti siklus pasang surut, gelombang suara, dan arus listrik. Grafik ini juga berperan penting dalam berbagai disiplin ilmu, teknologi, dan seni.
Penerapan dalam Kehidupan Sehari-hari
Grafik trigonometri dapat ditemukan dalam berbagai aspek kehidupan sehari-hari, meskipun kita mungkin tidak menyadarinya. Berikut beberapa contohnya:
- Siklus Pasang Surut: Pasang surut air laut merupakan contoh fenomena periodik yang dapat dimodelkan dengan fungsi trigonometri. Grafik sinus atau kosinus dapat digunakan untuk memprediksi waktu dan ketinggian pasang surut di suatu lokasi tertentu.
- Gelombang Suara: Suara yang kita dengar merupakan gelombang yang merambat melalui udara. Grafik trigonometri, khususnya grafik sinus, dapat digunakan untuk menggambarkan bentuk gelombang suara, yang menentukan frekuensi dan amplitudo suara.
- Arus Listrik: Arus listrik bolak-balik (AC) yang mengalir di rumah kita juga merupakan contoh fenomena periodik. Grafik sinus dapat digunakan untuk menggambarkan bentuk gelombang arus listrik, yang menentukan frekuensi dan tegangan arus.
Penerapan dalam Ilmu Pengetahuan
Grafik trigonometri merupakan alat penting dalam berbagai bidang ilmu pengetahuan, seperti fisika, kimia, dan biologi.
- Fisika: Grafik trigonometri digunakan untuk menganalisis gerak harmonik sederhana, seperti ayunan bandul, serta gelombang cahaya dan suara. Grafik ini juga berperan dalam mempelajari fenomena elektromagnetik dan mekanika fluida.
- Kimia: Grafik trigonometri digunakan untuk memodelkan reaksi kimia periodik, seperti osilasi kimia, dan untuk menganalisis spektrum cahaya yang dipancarkan oleh atom dan molekul.
- Biologi: Grafik trigonometri digunakan untuk memodelkan siklus hidup organisme, seperti siklus reproduksi dan pertumbuhan, serta untuk menganalisis data biologis yang bersifat periodik, seperti denyut jantung dan aktivitas otak.
Penerapan dalam Teknologi
Grafik trigonometri memainkan peran penting dalam berbagai teknologi modern, seperti telekomunikasi, navigasi, dan pemrosesan sinyal.
Contoh soal grafik trigonometri bisa membantu kamu memahami bagaimana fungsi trigonometri ditampilkan secara visual. Misalnya, soal tentang menentukan amplitudo, periode, dan pergeseran fase dari suatu grafik sinus. Nah, kalau kamu mau belajar tentang perhitungan pajak, kamu bisa cek contoh soal PPh Badan dan koreksi fiskal beserta jawabannya di sini.
Setelah memahami konsep PPh Badan, kamu bisa kembali ke contoh soal grafik trigonometri untuk memperdalam pemahamanmu tentang fungsi trigonometri.
- Telekomunikasi: Grafik trigonometri digunakan dalam sistem komunikasi nirkabel, seperti telepon seluler dan jaringan Wi-Fi, untuk memodelkan dan menganalisis gelombang radio. Grafik ini juga digunakan dalam sistem GPS untuk menentukan lokasi dan navigasi.
- Navigasi: Grafik trigonometri digunakan dalam sistem navigasi berbasis satelit, seperti GPS, untuk menentukan lokasi dan arah. Grafik ini juga digunakan dalam sistem autopilot pesawat terbang dan kapal laut.
- Pemrosesan Sinyal: Grafik trigonometri digunakan dalam pemrosesan sinyal audio dan video, seperti kompresi data, pengenalan suara, dan pengolahan citra. Grafik ini membantu dalam memisahkan sinyal yang diinginkan dari noise dan meningkatkan kualitas sinyal.
Penerapan dalam Seni
Grafik trigonometri tidak hanya terbatas pada ilmu pengetahuan dan teknologi, tetapi juga memiliki aplikasi dalam seni. Grafik ini dapat digunakan untuk menciptakan bentuk dan pola yang menarik.
- Arsitektur: Grafik trigonometri dapat digunakan untuk mendesain struktur bangunan yang stabil dan menarik. Contohnya, penggunaan kurva sinus dan kosinus dalam arsitektur modern menciptakan efek visual yang unik.
- Musik: Grafik trigonometri dapat digunakan untuk menganalisis nada dan harmoni dalam musik. Grafik ini membantu dalam memahami frekuensi dan amplitudo suara yang berbeda dalam komposisi musik.
- Seni Rupa: Grafik trigonometri dapat digunakan untuk menciptakan karya seni yang unik. Contohnya, penggunaan fungsi trigonometri dalam software desain grafis dapat menghasilkan pola dan bentuk yang rumit dan menarik.
Tabel Penerapan Grafik Trigonometri
| Bidang | Penerapan | Contoh |
|---|---|---|
| Kehidupan Sehari-hari | Siklus Pasang Surut, Gelombang Suara, Arus Listrik | Prediksi pasang surut, analisis bentuk gelombang suara, pengukuran arus listrik |
| Ilmu Pengetahuan | Gerak Harmonik Sederhana, Reaksi Kimia Periodik, Analisis Data Biologis | Analisis gerakan bandul, pemodelan osilasi kimia, analisis denyut jantung |
| Teknologi | Telekomunikasi, Navigasi, Pemrosesan Sinyal | Sistem komunikasi nirkabel, sistem GPS, pengolahan audio dan video |
| Seni | Arsitektur, Musik, Seni Rupa | Desain bangunan, analisis harmoni musik, pembuatan pola seni |
Soal-Soal Grafik Trigonometri
Grafik fungsi trigonometri merupakan representasi visual dari perilaku fungsi sinus, cosinus, dan tangen. Grafik ini membantu kita memahami hubungan antara sudut dan nilai fungsi trigonometri, serta bagaimana perubahan sudut mempengaruhi nilai fungsi tersebut. Untuk memahami konsep grafik fungsi trigonometri, kita dapat mengerjakan beberapa contoh soal. Soal-soal ini akan menguji kemampuan kita dalam menentukan nilai fungsi trigonometri dari grafik, menentukan persamaan grafik fungsi trigonometri, dan menentukan transformasi grafik fungsi trigonometri.
Menentukan Nilai Fungsi Trigonometri dari Grafik
Contoh soal ini akan membantu kita memahami bagaimana membaca nilai fungsi trigonometri dari grafik. Kita akan diberikan grafik fungsi trigonometri dan diminta untuk menentukan nilai fungsi pada sudut tertentu.
- Misalnya, diberikan grafik fungsi sinus dengan amplitudo 2 dan periode 360 derajat. Tentukan nilai fungsi sinus pada sudut 90 derajat dan 270 derajat.
- Grafik fungsi cosinus memiliki amplitudo 1 dan periode 180 derajat. Tentukan nilai fungsi cosinus pada sudut 45 derajat dan 135 derajat.
Menentukan Persamaan Grafik Fungsi Trigonometri
Contoh soal ini akan menguji kemampuan kita dalam menuliskan persamaan fungsi trigonometri dari grafik yang diberikan. Kita akan diberikan grafik fungsi trigonometri dan diminta untuk menentukan persamaan yang mewakili grafik tersebut.
- Misalnya, diberikan grafik fungsi sinus dengan amplitudo 3, periode 180 derajat, dan titik potong sumbu y di (0, 2). Tentukan persamaan fungsi sinus yang sesuai dengan grafik tersebut.
- Grafik fungsi cosinus memiliki amplitudo 2, periode 360 derajat, dan titik potong sumbu y di (0, 1). Tentukan persamaan fungsi cosinus yang sesuai dengan grafik tersebut.
Menentukan Transformasi Grafik Fungsi Trigonometri
Contoh soal ini akan menguji kemampuan kita dalam menentukan transformasi yang terjadi pada grafik fungsi trigonometri. Kita akan diberikan grafik fungsi trigonometri dan diminta untuk menentukan transformasi yang telah diterapkan pada fungsi dasar.
- Misalnya, diberikan grafik fungsi sinus dasar dan grafik fungsi sinus yang telah ditransformasikan. Tentukan transformasi yang telah diterapkan pada fungsi sinus dasar, seperti pergeseran horizontal, vertikal, atau perubahan amplitudo dan periode.
- Grafik fungsi cosinus dasar dan grafik fungsi cosinus yang telah ditransformasikan diberikan. Tentukan transformasi yang telah diterapkan pada fungsi cosinus dasar, seperti refleksi, pergeseran horizontal, vertikal, atau perubahan amplitudo dan periode.
Penyelesaian Soal Grafik Trigonometri
Grafik fungsi trigonometri merupakan representasi visual dari perilaku fungsi trigonometri seperti sinus, cosinus, dan tangen. Mempelajari grafik ini penting karena memungkinkan kita untuk memahami dengan lebih baik sifat-sifat fungsi trigonometri, seperti periode, amplitudo, dan pergeseran fase. Grafik fungsi trigonometri juga dapat digunakan untuk menyelesaikan berbagai macam soal, seperti menentukan nilai fungsi trigonometri, menentukan persamaan grafik, dan menentukan transformasi grafik.
Menentukan Nilai Fungsi Trigonometri dari Grafik
Untuk menentukan nilai fungsi trigonometri dari grafik, kita perlu memahami hubungan antara titik-titik pada grafik dan nilai fungsi trigonometri yang bersesuaian. Berikut adalah langkah-langkah yang dapat digunakan:
- Tentukan periode grafik. Periode adalah jarak horizontal yang dibutuhkan grafik untuk menyelesaikan satu siklus lengkap.
- Tentukan amplitudo grafik. Amplitudo adalah jarak vertikal dari garis tengah grafik ke titik puncak atau lembah.
- Tentukan pergeseran fase grafik. Pergeseran fase adalah jarak horizontal yang grafik digeser dari posisi asalnya.
- Gunakan informasi di atas untuk menentukan persamaan fungsi trigonometri yang sesuai dengan grafik.
- Substitusikan nilai x yang diberikan ke dalam persamaan fungsi trigonometri untuk mendapatkan nilai fungsi trigonometri yang sesuai.
Menentukan Persamaan Grafik Fungsi Trigonometri
Untuk menentukan persamaan grafik fungsi trigonometri, kita perlu memahami hubungan antara sifat-sifat grafik dan parameter fungsi trigonometri. Berikut adalah langkah-langkah yang dapat digunakan:
- Tentukan periode grafik. Periode adalah jarak horizontal yang dibutuhkan grafik untuk menyelesaikan satu siklus lengkap.
- Tentukan amplitudo grafik. Amplitudo adalah jarak vertikal dari garis tengah grafik ke titik puncak atau lembah.
- Tentukan pergeseran fase grafik. Pergeseran fase adalah jarak horizontal yang grafik digeser dari posisi asalnya.
- Tentukan jenis fungsi trigonometri yang sesuai dengan grafik (sinus, cosinus, atau tangen).
- Gunakan informasi di atas untuk menyusun persamaan fungsi trigonometri yang sesuai dengan grafik.
Menentukan Transformasi Grafik Fungsi Trigonometri
Transformasi grafik fungsi trigonometri meliputi perubahan pada bentuk, posisi, atau ukuran grafik. Transformasi ini dapat dilakukan dengan mengubah parameter fungsi trigonometri, seperti amplitudo, periode, pergeseran fase, dan pergeseran vertikal. Berikut adalah langkah-langkah yang dapat digunakan untuk menentukan transformasi grafik fungsi trigonometri:
- Tentukan jenis transformasi yang dilakukan pada grafik (misalnya, pergeseran horizontal, pergeseran vertikal, pencerminan, atau peregangan).
- Tentukan parameter fungsi trigonometri yang perlu diubah untuk menghasilkan transformasi yang diinginkan.
- Gunakan informasi di atas untuk menyusun persamaan fungsi trigonometri yang sesuai dengan grafik yang telah ditransformasikan.
Tips dan Trik Mengerjakan Soal Grafik Trigonometri
Grafik trigonometri merupakan representasi visual dari fungsi trigonometri seperti sinus, cosinus, dan tangen. Memahami konsep grafik trigonometri sangat penting untuk menyelesaikan berbagai soal, baik dalam matematika maupun bidang lainnya seperti fisika dan teknik. Artikel ini akan memberikan beberapa tips dan trik untuk membantu kamu dalam memahami konsep grafik trigonometri dan menyelesaikan soal-soal yang berkaitan dengannya.
Memahami Konsep Dasar Grafik Trigonometri
Untuk memahami konsep grafik trigonometri, ada beberapa hal penting yang perlu kamu perhatikan:
- Periode: Periode merupakan jarak horizontal yang dibutuhkan fungsi trigonometri untuk menyelesaikan satu siklus lengkap. Misalnya, periode fungsi sinus dan cosinus adalah 2π, sedangkan periode fungsi tangen adalah π.
- Amplitudo: Amplitudo adalah jarak vertikal dari garis tengah grafik ke titik puncak atau titik lembah. Amplitudo fungsi sinus dan cosinus adalah 1, sedangkan amplitudo fungsi tangen tidak terbatas.
- Garis Tengah: Garis tengah adalah garis horizontal yang membagi grafik menjadi dua bagian yang sama. Garis tengah fungsi sinus dan cosinus adalah y = 0, sedangkan garis tengah fungsi tangen tidak ada.
- Pergeseran Fase: Pergeseran fase adalah pergeseran horizontal grafik ke kanan atau kiri. Pergeseran fase dapat ditentukan dengan melihat nilai konstanta dalam fungsi trigonometri. Misalnya, fungsi y = sin(x + π/2) mengalami pergeseran fase π/2 ke kiri.
Tips dan Trik Menyelesaikan Soal Grafik Trigonometri
Berikut beberapa tips dan trik yang dapat membantu kamu dalam menyelesaikan soal grafik trigonometri dengan cepat dan tepat:
- Kenali Fungsi Trigonometri Dasar: Pastikan kamu sudah memahami bentuk grafik fungsi sinus, cosinus, dan tangen. Hal ini akan membantu kamu dalam menganalisis dan menyelesaikan soal dengan lebih mudah.
- Gunakan Tabel Nilai: Membuat tabel nilai dapat membantu kamu dalam menggambar grafik fungsi trigonometri. Tabel nilai berisi pasangan nilai x dan y yang memenuhi persamaan fungsi trigonometri.
- Perhatikan Periode dan Amplitudo: Periode dan amplitudo merupakan informasi penting yang dapat membantu kamu dalam mengidentifikasi fungsi trigonometri dan menggambar grafiknya dengan tepat.
- Manfaatkan Pergeseran Fase: Pergeseran fase dapat membantu kamu dalam menentukan titik-titik penting pada grafik, seperti titik potong dengan sumbu x dan sumbu y.
- Latih Soal-Soal: Melatih soal-soal secara rutin akan membantu kamu dalam memahami konsep dan meningkatkan kemampuan dalam menyelesaikan soal grafik trigonometri.
Contoh Soal dan Pembahasan
Berikut adalah contoh soal dan pembahasannya untuk mengilustrasikan tips dan trik yang telah dijelaskan:
Contoh Soal 1:
Gambarlah grafik fungsi y = 2sin(x + π/4) untuk 0 ≤ x ≤ 2π.
Pembahasan:
Dari persamaan fungsi, kita dapat melihat bahwa:
- Amplitudo = 2
- Periode = 2π
- Pergeseran fase = π/4 ke kiri
Untuk menggambar grafik, kita dapat membuat tabel nilai dengan beberapa titik x:
| x | y = 2sin(x + π/4) |
|---|---|
| 0 | 2sin(π/4) = √2 |
| π/4 | 2sin(π/2) = 2 |
| π/2 | 2sin(3π/4) = √2 |
| 3π/4 | 2sin(π) = 0 |
| π | 2sin(5π/4) = -√2 |
| 5π/4 | 2sin(3π/2) = -2 |
| 3π/2 | 2sin(7π/4) = -√2 |
| 7π/4 | 2sin(2π) = 0 |
| 2π | 2sin(9π/4) = √2 |
Dengan menggunakan tabel nilai, kita dapat menggambar grafik fungsi y = 2sin(x + π/4) sebagai berikut:
[Gambar grafik fungsi y = 2sin(x + π/4)]
Dari grafik tersebut, kita dapat melihat bahwa fungsi memiliki amplitudo 2, periode 2π, dan mengalami pergeseran fase π/4 ke kiri.
Latihan Soal Grafik Trigonometri
Untuk memahami konsep grafik trigonometri dengan lebih baik, mari kita berlatih dengan beberapa soal. Soal-soal berikut dirancang untuk menguji pemahamanmu tentang fungsi trigonometri, periodisitas, amplitudo, dan fase. Selamat mencoba!
Soal Latihan 1
Gambarlah grafik fungsi y = sin(x) untuk 0 ≤ x ≤ 2π.
Untuk menyelesaikan soal ini, kita perlu mengingat sifat dasar fungsi sinus. Fungsi sinus memiliki periodisitas 2π, artinya grafiknya akan berulang setiap 2π satuan. Amplitudo fungsi sinus adalah 1, artinya nilai maksimum dan minimumnya adalah 1 dan -1. Kita juga perlu mengingat beberapa titik penting pada grafik fungsi sinus, seperti (0, 0), (π/2, 1), (π, 0), (3π/2, -1), dan (2π, 0).
Dengan menggunakan informasi di atas, kita dapat menggambar grafik fungsi y = sin(x) seperti berikut:
Gambarlah sumbu x dan y.
Tandai titik-titik penting pada sumbu x: 0, π/2, π, 3π/2, dan 2π.
Tandai titik-titik penting pada sumbu y: 1 dan -1.
Hubungkan titik-titik tersebut dengan garis lengkung yang halus.
Soal Latihan 2
Gambarlah grafik fungsi y = 2 cos(x) untuk -π ≤ x ≤ π.
Soal ini serupa dengan soal sebelumnya, hanya saja fungsi yang digunakan adalah cosinus dan amplitudonya adalah 2. Fungsi cosinus juga memiliki periodisitas 2π. Untuk menggambar grafiknya, kita perlu mengingat titik-titik penting pada grafik fungsi cosinus, seperti (0, 1), (π/2, 0), (π, -1), (3π/2, 0), dan (2π, 1).
Dengan menggunakan informasi di atas, kita dapat menggambar grafik fungsi y = 2 cos(x) seperti berikut:
Gambarlah sumbu x dan y.
Tandai titik-titik penting pada sumbu x: -π, -π/2, 0, π/2, dan π.
Tandai titik-titik penting pada sumbu y: 2 dan -2.
Hubungkan titik-titik tersebut dengan garis lengkung yang halus.
Soal Latihan 3, Contoh soal grafik trigonometri
Gambarlah grafik fungsi y = sin(2x) untuk 0 ≤ x ≤ π.
Soal ini melibatkan perubahan pada periode fungsi sinus. Faktor 2 di dalam fungsi sinus menyebabkan periodenya menjadi π, bukan 2π. Artinya, grafik akan berulang setiap π satuan. Amplitudo fungsi tetap 1. Titik-titik penting pada grafik fungsi y = sin(2x) adalah (0, 0), (π/4, 1), (π/2, 0), (3π/4, -1), dan (π, 0).
Dengan menggunakan informasi di atas, kita dapat menggambar grafik fungsi y = sin(2x) seperti berikut:
Gambarlah sumbu x dan y.
Tandai titik-titik penting pada sumbu x: 0, π/4, π/2, 3π/4, dan π.
Tandai titik-titik penting pada sumbu y: 1 dan -1.
Hubungkan titik-titik tersebut dengan garis lengkung yang halus.
Soal Latihan 4
Gambarlah grafik fungsi y = cos(x – π/2) untuk 0 ≤ x ≤ 2π.
Soal ini melibatkan perubahan pada fase fungsi cosinus. Faktor -π/2 di dalam fungsi cosinus menyebabkan grafiknya bergeser ke kanan sebesar π/2 satuan. Periode dan amplitudo fungsi tetap sama, yaitu 2π dan 1. Titik-titik penting pada grafik fungsi y = cos(x – π/2) adalah (π/2, 1), (π, 0), (3π/2, -1), (2π, 0), dan (5π/2, 1).
Dengan menggunakan informasi di atas, kita dapat menggambar grafik fungsi y = cos(x – π/2) seperti berikut:
Gambarlah sumbu x dan y.
Tandai titik-titik penting pada sumbu x: 0, π/2, π, 3π/2, 2π, dan 5π/2.
Tandai titik-titik penting pada sumbu y: 1 dan -1.
Hubungkan titik-titik tersebut dengan garis lengkung yang halus.
Soal Latihan 5
Gambarlah grafik fungsi y = 3 sin(x + π/4) untuk -π/4 ≤ x ≤ 7π/4.
Soal ini melibatkan perubahan pada amplitudo, fase, dan periode fungsi sinus. Amplitudo fungsi adalah 3, fase fungsi adalah π/4, dan periodenya adalah 2π. Titik-titik penting pada grafik fungsi y = 3 sin(x + π/4) adalah (-π/4, 0), (0, 3√2/2), (π/4, 3), (π/2, 3√2/2), (π, 0), (5π/4, -3√2/2), (3π/2, -3), (7π/4, -3√2/2).
Dengan menggunakan informasi di atas, kita dapat menggambar grafik fungsi y = 3 sin(x + π/4) seperti berikut:
Gambarlah sumbu x dan y.
Tandai titik-titik penting pada sumbu x: -π/4, 0, π/4, π/2, π, 5π/4, 3π/2, dan 7π/4.
Tandai titik-titik penting pada sumbu y: 3 dan -3.
Hubungkan titik-titik tersebut dengan garis lengkung yang halus.
Referensi dan Sumber Belajar
Memahami grafik trigonometri memerlukan eksplorasi lebih dalam, dan sumber belajar yang tepat akan membantu Anda menguasainya. Artikel ini akan memberikan panduan lengkap mengenai referensi dan sumber belajar yang dapat Anda akses untuk mempelajari grafik trigonometri secara lebih mendalam.
Buku Teks
Buku teks matematika tingkat menengah atas atau perguruan tinggi biasanya memuat bab khusus tentang trigonometri, termasuk grafik trigonometri. Berikut beberapa buku teks yang dapat Anda pertimbangkan:
- Matematika untuk SMA Kelas 10 oleh Erlangga
- Trigonometri oleh Anton dan Bivens
- Calculus oleh Thomas dan Finney
Website
Internet menawarkan berbagai sumber belajar online yang dapat membantu Anda memahami grafik trigonometri. Berikut beberapa website yang dapat Anda kunjungi:
- Khan Academy: Situs web ini menyediakan video tutorial, latihan, dan penjelasan yang mudah dipahami tentang trigonometri, termasuk grafik trigonometri.
- MathPlanet: Situs web ini menyediakan materi pembelajaran tentang trigonometri, termasuk grafik trigonometri, dengan penjelasan yang detail dan contoh soal yang beragam.
- Wolfram Alpha: Situs web ini menawarkan kalkulator online yang dapat digunakan untuk menggambar grafik fungsi trigonometri dan mendapatkan informasi lebih lanjut tentang fungsi tersebut.
Video Tutorial
Video tutorial dapat menjadi cara yang efektif untuk mempelajari grafik trigonometri. Berikut beberapa saluran YouTube yang menyediakan video tutorial tentang grafik trigonometri:
- Khan Academy: Saluran YouTube ini menyediakan video tutorial yang komprehensif tentang trigonometri, termasuk grafik trigonometri, dengan penjelasan yang mudah dipahami.
- 3Blue1Brown: Saluran YouTube ini menawarkan video tutorial yang kreatif dan inovatif tentang matematika, termasuk trigonometri, dengan visualisasi yang menarik.
- The Organic Chemistry Tutor: Saluran YouTube ini menyediakan video tutorial tentang berbagai topik matematika, termasuk trigonometri, dengan penjelasan yang jelas dan ringkas.
Sumber Belajar Lainnya
Selain buku teks, website, dan video tutorial, Anda dapat menggunakan sumber belajar lain untuk mempelajari grafik trigonometri. Berikut beberapa rekomendasi:
- Aplikasi mobile: Aplikasi mobile seperti GeoGebra dan Desmos dapat membantu Anda menggambar grafik fungsi trigonometri secara interaktif dan mempelajari sifat-sifatnya.
- Forum diskusi online: Bergabung dengan forum diskusi online tentang matematika dapat membantu Anda mendapatkan bantuan dari para ahli dan berdiskusi dengan siswa lain tentang topik yang sedang Anda pelajari.
- Kursus online: Kursus online seperti Coursera dan edX menawarkan kursus tentang trigonometri yang dapat membantu Anda mempelajari grafik trigonometri secara sistematis.
Kesimpulan
Memahami grafik trigonometri tidak hanya membuka pintu untuk menyelesaikan soal matematika, tetapi juga untuk memahami dan menganalisis berbagai fenomena alam dan teknologi yang melibatkan pola periodik. Dengan pengetahuan ini, Anda dapat melihat dunia dengan sudut pandang yang lebih luas dan menemukan keindahan matematika dalam berbagai aspek kehidupan.





