Contoh soal ketidakpastian pengukuran berulang – Dalam dunia ilmu pengetahuan, pengukuran merupakan hal yang fundamental. Namun, tak jarang hasil pengukuran yang kita peroleh tidak selalu akurat. Ketidakpastian pengukuran berulang muncul karena berbagai faktor, seperti kesalahan alat ukur, kesalahan pengamat, dan variasi kondisi lingkungan. Ketidakpastian ini memengaruhi keakuratan hasil pengukuran dan perlu dipahami agar kita bisa menafsirkan data dengan tepat.
Contoh soal ketidakpastian pengukuran berulang membantu kita memahami bagaimana cara menghitung dan menafsirkan ketidakpastian dalam pengukuran. Dengan memahami konsep ini, kita dapat menilai keakuratan hasil pengukuran dan meningkatkan kepercayaan terhadap data yang kita peroleh.
Pengertian Ketidakpastian Pengukuran Berulang
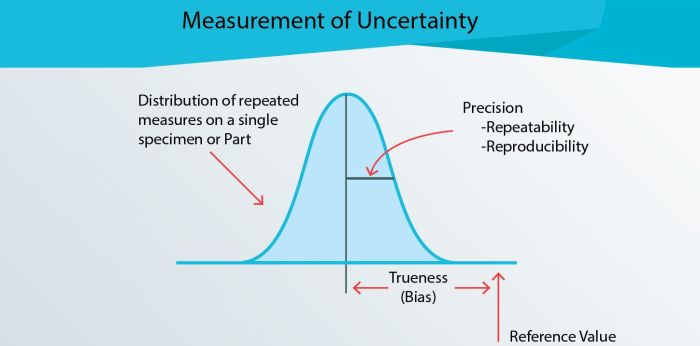
Dalam dunia fisika, pengukuran merupakan kegiatan penting untuk mendapatkan data kuantitatif yang menggambarkan suatu fenomena. Namun, tidak semua pengukuran dapat dilakukan dengan sempurna dan menghasilkan nilai yang sama persis setiap kali dilakukan. Ketidakpastian pengukuran berulang muncul karena berbagai faktor, seperti keterbatasan alat ukur, pengaruh lingkungan, dan bahkan kesalahan manusia.
Ketidakpastian Pengukuran Berulang dalam Konteks Fisika
Ketidakpastian pengukuran berulang merujuk pada variasi atau penyimpangan nilai yang diperoleh dari pengukuran yang sama yang dilakukan berulang kali dalam kondisi yang sama atau hampir sama. Ketidakpastian ini menunjukkan bahwa hasil pengukuran tidak selalu tepat dan pasti, tetapi memiliki rentang nilai yang mungkin.
Contoh Kasus Ketidakpastian Pengukuran Berulang
Bayangkan Anda ingin mengukur panjang meja menggunakan penggaris. Jika Anda mengukur meja beberapa kali, Anda mungkin mendapatkan hasil yang sedikit berbeda setiap kali. Hal ini bisa disebabkan oleh berbagai faktor, seperti:
- Posisi mata Anda saat membaca skala penggaris tidak selalu sama.
- Penggaris mungkin sedikit bengkok atau tidak lurus sempurna.
- Permukaan meja mungkin tidak rata.
Ketidakpastian pengukuran berulang dalam kasus ini menunjukkan bahwa panjang meja tidak memiliki nilai pasti, tetapi memiliki rentang nilai yang mungkin.
Dampak Ketidakpastian Pengukuran Berulang terhadap Keakuratan
Ketidakpastian pengukuran berulang memiliki dampak yang signifikan terhadap keakuratan hasil pengukuran. Semakin besar ketidakpastian, semakin rendah keakuratan hasil pengukuran. Misalnya, jika Anda mengukur panjang meja beberapa kali dan mendapatkan hasil yang sangat bervariasi, maka Anda tidak dapat yakin dengan keakuratan hasil pengukuran tersebut.
Untuk meningkatkan keakuratan hasil pengukuran, penting untuk meminimalkan ketidakpastian pengukuran berulang. Hal ini dapat dilakukan dengan:
- Menggunakan alat ukur yang lebih presisi.
- Mengontrol kondisi lingkungan yang dapat memengaruhi pengukuran.
- Melakukan pengukuran berulang kali dan menghitung nilai rata-rata.
Sumber Ketidakpastian Pengukuran Berulang
Dalam melakukan pengukuran berulang, kita seringkali mendapati bahwa hasil pengukuran tidak selalu sama persis. Hal ini menunjukkan bahwa terdapat ketidakpastian dalam proses pengukuran. Ketidakpastian ini bisa berasal dari berbagai sumber, baik dari alat ukur yang kita gunakan, kesalahan pengamat, maupun variasi kondisi lingkungan.
Kesalahan Alat Ukur
Kesalahan alat ukur merupakan salah satu sumber utama ketidakpastian dalam pengukuran berulang. Setiap alat ukur memiliki batas kemampuan dalam menunjukkan nilai yang akurat. Hal ini disebabkan oleh beberapa faktor, seperti:
- Keakuratan Alat Ukur: Setiap alat ukur memiliki batas keakuratan yang ditentukan oleh produsen. Misalnya, sebuah mistar ukur dengan skala 1 mm memiliki keakuratan 1 mm. Artinya, nilai yang ditunjukkan oleh mistar ukur tersebut dapat bervariasi hingga 1 mm dari nilai sebenarnya.
- Kalibrasi Alat Ukur: Alat ukur perlu dikalibrasi secara berkala untuk memastikan keakuratannya. Jika alat ukur tidak dikalibrasi, maka nilai yang ditunjukkannya akan menyimpang dari nilai sebenarnya. Misalnya, sebuah termometer yang tidak dikalibrasi dapat menunjukkan suhu yang lebih tinggi atau lebih rendah dari suhu sebenarnya.
- Kondisi Fisik Alat Ukur: Kondisi fisik alat ukur juga dapat memengaruhi keakuratannya. Misalnya, sebuah neraca pegas yang rusak dapat menunjukkan berat yang lebih tinggi atau lebih rendah dari berat sebenarnya.
Kesalahan Pengamat
Kesalahan pengamat juga merupakan sumber ketidakpastian yang signifikan dalam pengukuran berulang. Hal ini disebabkan oleh beberapa faktor, seperti:
- Kesalahan Membaca Skala: Pengamat dapat melakukan kesalahan dalam membaca skala alat ukur, seperti membaca skala terlalu tinggi atau terlalu rendah. Hal ini dapat terjadi karena kurangnya ketelitian atau kurangnya pengalaman dalam membaca skala alat ukur.
- Kesalahan Menentukan Titik Nol: Pengamat dapat melakukan kesalahan dalam menentukan titik nol pada alat ukur, seperti menentukan titik nol terlalu tinggi atau terlalu rendah. Hal ini dapat terjadi karena kurangnya ketelitian atau kurangnya pengalaman dalam menggunakan alat ukur.
- Kesalahan dalam Menjalankan Prosedur: Pengamat dapat melakukan kesalahan dalam menjalankan prosedur pengukuran, seperti mengukur dengan sudut yang salah atau mengukur dengan tekanan yang tidak konsisten. Hal ini dapat terjadi karena kurangnya pemahaman terhadap prosedur pengukuran atau kurangnya latihan dalam menjalankan prosedur tersebut.
Variasi Kondisi Lingkungan
Variasi kondisi lingkungan juga dapat memengaruhi hasil pengukuran berulang. Hal ini disebabkan oleh beberapa faktor, seperti:
- Suhu: Suhu dapat memengaruhi ukuran benda. Misalnya, sebuah batang logam akan memuai saat dipanaskan dan menyusut saat didinginkan. Hal ini dapat memengaruhi hasil pengukuran panjang batang logam.
- Tekanan: Tekanan juga dapat memengaruhi ukuran benda. Misalnya, sebuah balon akan mengembang saat tekanan udara di sekitarnya meningkat dan menyusut saat tekanan udara di sekitarnya menurun. Hal ini dapat memengaruhi hasil pengukuran volume balon.
- Kelembaban: Kelembaban dapat memengaruhi ukuran benda, terutama benda yang terbuat dari bahan higroskopis, seperti kayu dan kertas. Misalnya, sebuah papan kayu akan memuai saat kelembaban udara meningkat dan menyusut saat kelembaban udara menurun. Hal ini dapat memengaruhi hasil pengukuran panjang papan kayu.
Cara Menentukan Ketidakpastian Pengukuran Berulang: Contoh Soal Ketidakpastian Pengukuran Berulang
Ketika kita melakukan pengukuran berulang, hasil yang kita peroleh tidak selalu sama persis. Ini karena terdapat ketidakpastian dalam proses pengukuran, seperti kesalahan pembacaan alat ukur, variasi kondisi lingkungan, atau fluktuasi instrumen. Ketidakpastian pengukuran berulang dapat dihitung dengan menggunakan metode statistik, yang membantu kita untuk memahami seberapa akurat hasil pengukuran kita.
Metode Statistik untuk Menentukan Ketidakpastian Pengukuran Berulang
Metode statistik yang umum digunakan untuk menentukan ketidakpastian pengukuran berulang adalah deviasi standar dan kesalahan absolut.
- Deviasi Standar merupakan ukuran penyebaran data sekitar nilai rata-rata. Deviasi standar yang lebih kecil menunjukkan bahwa data lebih terkonsentrasi di sekitar nilai rata-rata, sedangkan deviasi standar yang lebih besar menunjukkan bahwa data lebih tersebar.
- Kesalahan Absolut adalah perbedaan antara nilai pengukuran dan nilai sebenarnya. Kesalahan absolut dapat positif atau negatif, tergantung pada apakah nilai pengukuran lebih besar atau lebih kecil dari nilai sebenarnya.
Contoh Perhitungan Ketidakpastian Pengukuran Berulang
Misalnya, kita ingin mengukur panjang suatu benda dengan menggunakan penggaris. Kita melakukan pengukuran berulang sebanyak 10 kali, dan memperoleh data berikut:
| Pengukuran ke- | Panjang (cm) |
|---|---|
| 1 | 10.1 |
| 2 | 10.2 |
| 3 | 10.0 |
| 4 | 10.3 |
| 5 | 10.1 |
| 6 | 10.2 |
| 7 | 10.1 |
| 8 | 10.0 |
| 9 | 10.2 |
| 10 | 10.1 |
Nilai rata-rata dari pengukuran ini adalah 10.12 cm. Deviasi standar dari data ini adalah 0.09 cm. Kesalahan absolut dari setiap pengukuran dapat dihitung dengan mengurangi nilai rata-rata dari setiap nilai pengukuran. Misalnya, kesalahan absolut dari pengukuran pertama adalah 10.1 – 10.12 = -0.02 cm.
Perbedaan Ketidakpastian Absolut dan Ketidakpastian Relatif
Ketidakpastian absolut dan ketidakpastian relatif merupakan dua cara untuk menyatakan ketidakpastian dalam pengukuran. Ketidakpastian absolut menunjukkan seberapa besar nilai pengukuran dapat berbeda dari nilai sebenarnya, sedangkan ketidakpastian relatif menunjukkan seberapa besar ketidakpastian absolut dibandingkan dengan nilai pengukuran.
- Ketidakpastian Absolut dinyatakan dalam satuan yang sama dengan nilai pengukuran. Misalnya, jika nilai pengukuran adalah 10 cm, maka ketidakpastian absolut dapat dinyatakan dalam cm.
- Ketidakpastian Relatif dinyatakan sebagai persentase atau pecahan dari nilai pengukuran. Misalnya, jika nilai pengukuran adalah 10 cm dan ketidakpastian absolut adalah 0.1 cm, maka ketidakpastian relatif adalah 0.1/10 = 0.01 atau 1%.
Contoh Penerapan Ketidakpastian Absolut dan Relatif
Misalnya, kita ingin mengukur massa suatu benda dengan menggunakan timbangan. Kita memperoleh hasil pengukuran 100 gram dengan ketidakpastian absolut 0.5 gram. Ketidakpastian relatif dari pengukuran ini adalah 0.5/100 = 0.005 atau 0.5%. Ini berarti bahwa massa benda sebenarnya dapat berada di antara 99.5 gram dan 100.5 gram.
Ketidakpastian absolut dan relatif berguna untuk mengevaluasi akurasi pengukuran dan untuk membandingkan hasil pengukuran dari berbagai sumber. Ketidakpastian absolut menunjukkan seberapa besar nilai pengukuran dapat berbeda dari nilai sebenarnya, sedangkan ketidakpastian relatif menunjukkan seberapa besar ketidakpastian absolut dibandingkan dengan nilai pengukuran.
Menampilkan Hasil Pengukuran Berulang
Setelah melakukan pengukuran berulang, penting untuk menampilkan hasil pengukuran tersebut secara tepat dan mudah dipahami. Menampilkan hasil pengukuran berulang dengan menyertakan ketidakpastiannya akan memberikan gambaran yang lebih lengkap tentang nilai yang diukur, termasuk tingkat ketelitian dan ketepatannya.
Menampilkan Hasil Pengukuran Berulang
Hasil pengukuran berulang dapat ditampilkan dalam berbagai bentuk, salah satunya adalah dengan menggunakan tabel. Tabel dapat membantu untuk menyajikan data secara terstruktur dan mudah dibaca. Berikut adalah contoh tabel yang menampilkan hasil pengukuran berulang beserta ketidakpastian absolut dan relatifnya:
| Pengukuran ke- | Nilai Pengukuran (cm) | Ketidakpastian Absolut (cm) | Ketidakpastian Relatif (%) |
|---|---|---|---|
| 1 | 10.2 | 0.1 | 0.98 |
| 2 | 10.1 | 0.1 | 0.99 |
| 3 | 10.3 | 0.1 | 0.97 |
| 4 | 10.2 | 0.1 | 0.98 |
| 5 | 10.0 | 0.1 | 1.00 |
Interpretasi Hasil Pengukuran Berulang
Interpretasi hasil pengukuran berulang yang ditampilkan dalam tabel dapat dilakukan dengan memperhatikan beberapa aspek, seperti:
- Nilai Rata-rata: Nilai rata-rata dari pengukuran berulang dapat memberikan estimasi terbaik dari nilai yang diukur. Dalam contoh tabel di atas, nilai rata-rata dari pengukuran panjang adalah 10.16 cm.
- Ketidakpastian Absolut: Ketidakpastian absolut menunjukkan batas atas dari kesalahan pengukuran. Dalam contoh tabel di atas, ketidakpastian absolut adalah 0.1 cm. Ini berarti bahwa nilai sebenarnya dari panjang yang diukur berada di antara 10.06 cm dan 10.26 cm.
- Ketidakpastian Relatif: Ketidakpastian relatif menunjukkan persentase kesalahan pengukuran terhadap nilai rata-rata. Dalam contoh tabel di atas, ketidakpastian relatif adalah 0.98%. Ini berarti bahwa kesalahan pengukuran kurang dari 1% dari nilai rata-rata.
- Penyebaran Data: Penyebaran data dalam tabel dapat menunjukkan tingkat ketelitian dan ketepatan pengukuran. Jika data tersebar secara merata di sekitar nilai rata-rata, maka pengukuran dapat dianggap teliti dan tepat. Sebaliknya, jika data tersebar secara tidak merata, maka pengukuran dapat dianggap tidak teliti atau tidak tepat.
Contoh Soal Ketidakpastian Pengukuran Berulang
Ketidakpastian pengukuran merupakan konsep penting dalam ilmu pengetahuan dan teknik. Ketika melakukan pengukuran berulang, nilai yang diperoleh tidak akan selalu sama persis. Hal ini disebabkan oleh berbagai faktor seperti kesalahan alat ukur, kesalahan manusia, dan faktor lingkungan. Ketidakpastian pengukuran berulang menunjukkan seberapa akurat hasil pengukuran kita. Untuk memahami konsep ini, mari kita bahas contoh soal berikut.
Contoh Soal
Seorang siswa ingin mengukur panjang sebuah benda dengan menggunakan jangka sorong. Ia melakukan pengukuran berulang sebanyak lima kali dan memperoleh data sebagai berikut:
| No. Pengukuran | Panjang (cm) |
|—|—|
| 1 | 5,25 |
| 2 | 5,23 |
| 3 | 5,26 |
| 4 | 5,24 |
| 5 | 5,27 |
Tentukanlah ketidakpastian absolut dan relatif dari pengukuran panjang benda tersebut!
Langkah-langkah Penyelesaian
Berikut langkah-langkah untuk menentukan ketidakpastian absolut dan relatif dari pengukuran panjang benda:
1. Menghitung Nilai Rata-rata
Nilai rata-rata (x̄) dari data pengukuran dapat dihitung dengan menjumlahkan semua nilai pengukuran dan membaginya dengan jumlah pengukuran.
x̄ = (5,25 + 5,23 + 5,26 + 5,24 + 5,27) / 5 = 5,25 cm
2. Menghitung Deviasi Standar
Deviasi standar (s) menunjukkan sebaran data pengukuran terhadap nilai rata-rata. Deviasi standar dapat dihitung dengan rumus berikut:
s = √[∑(xi – x̄)2 / (n – 1)]
di mana:
* xi adalah nilai pengukuran ke-i
* x̄ adalah nilai rata-rata
* n adalah jumlah pengukuran
Dengan menggunakan rumus tersebut, deviasi standar dari data pengukuran adalah:
s = √[(0,002 + (-0,02)2 + (0,01)2 + (-0,01)2 + (0,02)2) / (5 – 1)] = 0,014 cm
3. Menentukan Ketidakpastian Absolut
Ketidakpastian absolut (Δx) adalah setengah dari deviasi standar.
Δx = s / 2 = 0,014 cm / 2 = 0,007 cm
4. Menentukan Ketidakpastian Relatif
Ketidakpastian relatif (δx) menunjukkan seberapa besar ketidakpastian absolut dibandingkan dengan nilai rata-rata.
δx = Δx / x̄ = 0,007 cm / 5,25 cm = 0,0013
Ketidakpastian relatif biasanya dinyatakan dalam bentuk persentase.
δx = 0,0013 x 100% = 0,13%
Hasil Perhitungan
Berikut tabel yang menunjukkan hasil perhitungan ketidakpastian pengukuran panjang benda:
| Jenis Ketidakpastian | Nilai |
|—|—|
| Ketidakpastian Absolut (Δx) | 0,007 cm |
| Ketidakpastian Relatif (δx) | 0,13% |
Kesimpulan
Berdasarkan perhitungan di atas, panjang benda tersebut adalah 5,25 ± 0,007 cm atau 5,25 cm dengan ketidakpastian 0,13%. Hal ini menunjukkan bahwa hasil pengukuran memiliki tingkat keakuratan yang cukup tinggi, dengan ketidakpastian relatif hanya 0,13%.
Penerapan Ketidakpastian Pengukuran Berulang dalam Penelitian
Ketidakpastian pengukuran berulang merupakan konsep penting dalam penelitian ilmiah, terutama dalam bidang-bidang seperti fisika, kimia, dan biologi. Konsep ini membantu kita memahami seberapa akurat hasil pengukuran kita dan seberapa yakin kita terhadap kesimpulan yang diambil berdasarkan data tersebut. Dalam penelitian, pengukuran berulang dilakukan untuk mengurangi pengaruh kesalahan acak dan meningkatkan keandalan data. Ketidakpastian pengukuran berulang menjadi alat penting untuk mengukur ketepatan data dan mengomunikasikan hasil penelitian secara transparan dan akurat.
Bagaimana Konsep Ketidakpastian Pengukuran Berulang Diterapkan dalam Penelitian Ilmiah?
Dalam penelitian ilmiah, konsep ketidakpastian pengukuran berulang diterapkan dengan menghitung deviasi standar dari serangkaian pengukuran berulang. Deviasi standar menunjukkan sebaran data dari nilai rata-rata. Semakin kecil deviasi standar, semakin akurat hasil pengukuran dan semakin yakin kita terhadap kesimpulan yang diambil.
Contohnya, dalam percobaan untuk menentukan massa suatu benda, peneliti mungkin melakukan beberapa pengukuran menggunakan neraca. Hasil pengukuran mungkin sedikit berbeda setiap kali. Untuk mendapatkan nilai massa yang paling akurat, peneliti menghitung rata-rata dari semua pengukuran dan menghitung deviasi standar. Deviasi standar menunjukkan ketidakpastian dalam pengukuran massa. Ketidakpastian ini kemudian digunakan untuk menentukan rentang nilai massa yang mungkin, yang mencakup nilai massa yang sebenarnya dengan tingkat kepercayaan tertentu.
Contoh Kasus Penelitian
Misalnya, dalam penelitian tentang efek pupuk terhadap pertumbuhan tanaman, peneliti mungkin mengukur tinggi tanaman setiap minggu selama beberapa bulan. Peneliti akan mengukur tinggi beberapa tanaman dalam kelompok kontrol (tanpa pupuk) dan beberapa tanaman dalam kelompok perlakuan (dengan pupuk). Untuk setiap kelompok, peneliti akan mendapatkan serangkaian data tinggi tanaman. Dengan menggunakan konsep ketidakpastian pengukuran berulang, peneliti dapat menentukan seberapa akurat pengukuran tinggi tanaman dan seberapa yakin mereka bahwa ada perbedaan signifikan antara pertumbuhan tanaman di kelompok kontrol dan kelompok perlakuan.
Dalam analisis data, peneliti akan mempertimbangkan ketidakpastian pengukuran berulang dengan melakukan uji statistik. Uji statistik membantu peneliti menentukan apakah perbedaan antara kelompok kontrol dan kelompok perlakuan signifikan secara statistik, yaitu apakah perbedaan tersebut tidak hanya karena kesalahan acak dalam pengukuran. Jika perbedaan signifikan secara statistik, peneliti dapat menyimpulkan bahwa pupuk memang memiliki efek yang signifikan terhadap pertumbuhan tanaman.
Dampak Ketidakpastian Pengukuran Berulang terhadap Kesimpulan Penelitian
Ketidakpastian pengukuran berulang sangat penting dalam penelitian karena memengaruhi kesimpulan yang dapat diambil dari data. Jika ketidakpastian pengukuran tinggi, kesimpulan penelitian mungkin tidak akurat atau tidak pasti. Sebaliknya, jika ketidakpastian pengukuran rendah, kesimpulan penelitian lebih akurat dan lebih dapat diandalkan.
Misalnya, jika peneliti menemukan bahwa tinggi tanaman di kelompok perlakuan lebih tinggi daripada tinggi tanaman di kelompok kontrol, tetapi ketidakpastian pengukuran tinggi, peneliti mungkin tidak dapat menyimpulkan bahwa pupuk memang memiliki efek yang signifikan terhadap pertumbuhan tanaman. Hal ini karena perbedaan tinggi tanaman mungkin hanya karena kesalahan acak dalam pengukuran. Namun, jika ketidakpastian pengukuran rendah, peneliti dapat lebih yakin bahwa perbedaan tinggi tanaman memang signifikan dan bahwa pupuk memiliki efek yang nyata terhadap pertumbuhan tanaman.
Menilai Keakuratan Pengukuran Berulang
Dalam dunia ilmiah, pengukuran merupakan hal yang fundamental. Pengukuran berulang dilakukan untuk mendapatkan hasil yang lebih akurat dan mengurangi dampak kesalahan acak. Namun, setiap pengukuran pasti memiliki ketidakpastian. Ketidakpastian ini menunjukkan rentang nilai yang mungkin untuk hasil pengukuran yang sebenarnya. Menilai keakuratan hasil pengukuran berulang berarti memahami bagaimana ketidakpastian mempengaruhi hasil akhir dan tingkat kepercayaan terhadap hasil tersebut.
Menilai Keakuratan dengan Memperhatikan Ketidakpastian
Untuk menilai keakuratan hasil pengukuran berulang, kita perlu mempertimbangkan ketidakpastiannya. Semakin kecil ketidakpastian, semakin akurat hasil pengukuran. Ketidakpastian dapat dinyatakan sebagai deviasi standar atau rentang nilai. Deviasi standar menunjukkan sebaran data di sekitar nilai rata-rata. Rentang nilai menunjukkan batas atas dan bawah yang mungkin untuk hasil pengukuran.
Contoh Perbandingan Keakuratan
Bayangkan kita melakukan pengukuran panjang meja dengan dua metode berbeda. Metode pertama menghasilkan nilai rata-rata 1,5 meter dengan deviasi standar 0,05 meter. Metode kedua menghasilkan nilai rata-rata 1,5 meter dengan deviasi standar 0,1 meter. Meskipun kedua metode menghasilkan nilai rata-rata yang sama, metode pertama lebih akurat karena deviasi standarnya lebih kecil. Ini menunjukkan bahwa pengukuran metode pertama lebih terkonsentrasi di sekitar nilai rata-rata, sehingga hasil pengukuran lebih dapat dipercaya.
Pengaruh Ketidakpastian terhadap Kepercayaan
Ketidakpastian pengukuran berulang memengaruhi kepercayaan terhadap hasil pengukuran. Semakin besar ketidakpastian, semakin rendah kepercayaan kita terhadap hasil tersebut. Ini karena semakin besar ketidakpastian, semakin lebar rentang nilai yang mungkin untuk hasil pengukuran yang sebenarnya. Dengan demikian, kita tidak dapat yakin bahwa hasil pengukuran yang kita peroleh benar-benar mewakili nilai yang sebenarnya.
Meningkatkan Keakuratan Pengukuran Berulang
Dalam dunia sains dan teknik, pengukuran berulang sangat penting untuk memperoleh hasil yang akurat dan dapat diandalkan. Namun, ketidakpastian dalam pengukuran berulang adalah hal yang umum terjadi. Oleh karena itu, penting untuk memahami cara-cara yang dapat dilakukan untuk meningkatkan keakuratan hasil pengukuran berulang.
Cara Meningkatkan Keakuratan Pengukuran Berulang
Ada beberapa cara untuk meningkatkan keakuratan hasil pengukuran berulang, yaitu dengan menggunakan alat ukur yang lebih presisi dan mengurangi variasi kondisi lingkungan.
- Gunakan alat ukur yang lebih presisi. Semakin presisi alat ukur yang digunakan, semakin kecil ketidakpastian yang dihasilkan. Misalnya, jika Anda mengukur panjang suatu benda, menggunakan jangka sorong akan memberikan hasil yang lebih akurat daripada menggunakan penggaris biasa.
- Kurangi variasi kondisi lingkungan. Variasi kondisi lingkungan, seperti suhu, kelembaban, dan tekanan udara, dapat mempengaruhi hasil pengukuran. Untuk meminimalkan pengaruh ini, usahakan untuk melakukan pengukuran dalam kondisi lingkungan yang terkontrol. Misalnya, jika Anda mengukur volume suatu cairan, lakukan pengukuran dalam ruangan yang ber-AC untuk menghindari perubahan suhu yang signifikan.
- Lakukan pengukuran berulang. Semakin banyak pengukuran yang dilakukan, semakin akurat hasil rata-ratanya. Hal ini dikarenakan kesalahan acak yang terjadi dalam setiap pengukuran cenderung saling meniadakan.
Contoh Praktik Terbaik dalam Melakukan Pengukuran Berulang
Berikut adalah beberapa contoh praktik terbaik dalam melakukan pengukuran berulang untuk meminimalkan ketidakpastian:
- Kalibrasi alat ukur secara berkala. Kalibrasi alat ukur secara berkala akan memastikan bahwa alat ukur tersebut masih akurat.
- Gunakan metode pengukuran yang tepat. Pilih metode pengukuran yang paling tepat untuk objek yang akan diukur. Misalnya, jika Anda mengukur diameter suatu benda bulat, gunakan jangka sorong, bukan penggaris.
- Catat semua data pengukuran. Catat semua data pengukuran, termasuk nilai pengukuran, tanggal, waktu, dan kondisi lingkungan. Hal ini akan membantu Anda untuk menganalisis hasil pengukuran dan mengidentifikasi sumber ketidakpastian.
Memilih Alat Ukur yang Tepat
Memilih alat ukur yang tepat sangat penting untuk mendapatkan hasil pengukuran yang akurat. Pertimbangan berikut dapat membantu Anda dalam memilih alat ukur yang tepat:
- Akurasi yang dibutuhkan. Tentukan tingkat akurasi yang dibutuhkan untuk pengukuran Anda. Jika Anda membutuhkan akurasi yang tinggi, Anda perlu memilih alat ukur yang memiliki presisi tinggi.
- Rentang pengukuran. Pilih alat ukur yang memiliki rentang pengukuran yang sesuai dengan objek yang akan diukur.
- Kemudahan penggunaan. Pilih alat ukur yang mudah digunakan dan dipahami.
- Biaya. Pertimbangkan biaya alat ukur.
Perbedaan Ketidakpastian Pengukuran Berulang dan Ketidakpastian Sistematis
Dalam dunia pengukuran, kita tidak pernah bisa mendapatkan hasil yang sempurna. Selalu ada ketidakpastian yang melekat pada setiap pengukuran. Ketidakpastian ini bisa disebabkan oleh berbagai faktor, seperti kesalahan manusia, keterbatasan alat ukur, atau faktor lingkungan. Ketidakpastian pengukuran dibedakan menjadi dua jenis: ketidakpastian pengukuran berulang dan ketidakpastian sistematis.
Contoh soal ketidakpastian pengukuran berulang seringkali melibatkan perhitungan rata-rata dan standar deviasi. Misalnya, jika kita mengukur panjang meja berkali-kali, hasilnya mungkin sedikit berbeda setiap kali. Untuk menganalisis data tersebut, kita perlu menghitung rata-rata dan standar deviasi untuk menentukan tingkat ketidakpastian pengukuran.
Nah, kalau bicara soal analisis data, kamu pasti familiar dengan rasio aktivitas, kan? Rasio aktivitas seperti rasio lancar dan rasio perputaran persediaan juga penting untuk mengukur efisiensi perusahaan. Untuk mempelajari lebih lanjut tentang rasio aktivitas, kamu bisa cek contoh soal rasio aktivitas ini.
Singkatnya, baik ketidakpastian pengukuran berulang maupun rasio aktivitas sama-sama penting untuk memahami data dan membuat keputusan yang tepat.
Perbedaan Ketidakpastian Pengukuran Berulang dan Ketidakpastian Sistematis
Ketidakpastian pengukuran berulang muncul akibat variasi acak dalam pengukuran berulang. Artinya, meskipun kita melakukan pengukuran dengan alat yang sama dan dalam kondisi yang sama, kita akan mendapatkan hasil yang sedikit berbeda setiap kali. Hal ini disebabkan oleh faktor-faktor acak yang tidak dapat dikontrol, seperti fluktuasi kecil dalam pembacaan alat ukur, gerakan tangan pengukur, atau variasi kecil dalam kondisi lingkungan. Sementara itu, ketidakpastian sistematis muncul akibat kesalahan sistematik yang konsisten dalam setiap pengukuran. Kesalahan sistematis ini biasanya disebabkan oleh faktor-faktor yang bersifat sistematik, seperti kalibrasi alat ukur yang salah, kesalahan dalam metode pengukuran, atau efek lingkungan yang konsisten.
Contoh Kasus
Misalnya, kita ingin mengukur panjang sebuah benda dengan menggunakan penggaris. Kita melakukan pengukuran berulang kali dan mendapatkan hasil yang sedikit berbeda setiap kali. Perbedaan ini menunjukkan adanya ketidakpastian pengukuran berulang. Namun, jika penggaris yang kita gunakan ternyata tidak terkalibrasi dengan benar, maka semua pengukuran yang kita lakukan akan memiliki kesalahan sistematis yang sama. Hal ini akan menyebabkan semua hasil pengukuran kita menjadi salah, meskipun kita melakukan pengukuran berulang kali.
Pengaruh terhadap Keakuratan Hasil Pengukuran
Ketidakpastian pengukuran berulang dan ketidakpastian sistematis memiliki pengaruh yang berbeda terhadap keakuratan hasil pengukuran. Ketidakpastian pengukuran berulang dapat dikurangi dengan melakukan pengukuran berulang kali dan kemudian menghitung rata-rata hasil pengukuran. Semakin banyak pengukuran yang dilakukan, semakin akurat hasil rata-ratanya. Ketidakpastian sistematis, di sisi lain, tidak dapat dikurangi dengan melakukan pengukuran berulang kali. Untuk mengurangi ketidakpastian sistematis, kita perlu memperbaiki kesalahan sistematik yang menyebabkannya. Misalnya, jika penggaris kita tidak terkalibrasi dengan benar, kita perlu mengkalibrasi ulang penggaris tersebut. Dengan memahami perbedaan antara ketidakpastian pengukuran berulang dan ketidakpastian sistematis, kita dapat melakukan pengukuran yang lebih akurat dan meminimalkan kesalahan dalam hasil pengukuran.
Aplikasi Ketidakpastian Pengukuran Berulang dalam Bidang Lainnya
Konsep ketidakpastian pengukuran berulang tidak hanya penting dalam bidang sains, tetapi juga memiliki aplikasi yang luas di berbagai disiplin ilmu lain, seperti teknik, kimia, dan biologi. Pemahaman tentang ketidakpastian dalam pengukuran berulang membantu para profesional di bidang-bidang ini untuk mendapatkan hasil yang lebih akurat, meminimalkan kesalahan, dan membuat keputusan yang lebih tepat.
Aplikasi Ketidakpastian Pengukuran Berulang dalam Teknik
Dalam bidang teknik, ketidakpastian pengukuran berulang digunakan dalam berbagai aplikasi, seperti:
- Perancangan dan konstruksi: Ketidakpastian dalam pengukuran dimensi dan kekuatan material dapat memengaruhi kekuatan dan stabilitas struktur. Pertimbangan ketidakpastian ini penting untuk memastikan struktur yang aman dan tahan lama.
- Kontrol kualitas: Dalam proses produksi, ketidakpastian pengukuran digunakan untuk menentukan toleransi produk dan memastikan bahwa produk akhir memenuhi standar yang telah ditetapkan.
- Kalibrasi instrumen: Instrumen pengukuran harus dikalibrasi secara berkala untuk memastikan keakuratannya. Ketidakpastian pengukuran berulang digunakan untuk menentukan tingkat keakuratan instrumen dan menentukan interval kalibrasi yang tepat.
Aplikasi Ketidakpastian Pengukuran Berulang dalam Kimia, Contoh soal ketidakpastian pengukuran berulang
Dalam kimia, ketidakpastian pengukuran berulang sangat penting untuk:
- Analisis kuantitatif: Ketidakpastian dalam pengukuran konsentrasi zat dapat memengaruhi hasil analisis kimia. Dengan mempertimbangkan ketidakpastian, para ahli kimia dapat menentukan tingkat kepercayaan pada hasil analisis mereka.
- Penelitian dan pengembangan: Ketidakpastian pengukuran berulang digunakan untuk menilai keandalan data eksperimen dan menentukan tingkat signifikansi hasil penelitian.
- Sintesis dan karakterisasi bahan: Ketidakpastian dalam pengukuran sifat fisik dan kimia bahan dapat memengaruhi kualitas dan kinerja bahan tersebut. Pertimbangan ketidakpastian ini penting untuk memastikan konsistensi dan reliabilitas dalam sintesis dan karakterisasi bahan.
Aplikasi Ketidakpastian Pengukuran Berulang dalam Biologi
Dalam biologi, ketidakpastian pengukuran berulang digunakan untuk:
- Penelitian medis: Ketidakpastian dalam pengukuran variabel biologis, seperti tekanan darah atau kadar gula darah, dapat memengaruhi hasil penelitian medis. Pertimbangan ketidakpastian ini penting untuk menentukan tingkat signifikansi hasil penelitian dan untuk membuat kesimpulan yang valid.
- Diagnosa penyakit: Ketidakpastian dalam pengukuran parameter biologis, seperti kadar protein atau enzim, dapat memengaruhi diagnosis penyakit. Pertimbangan ketidakpastian ini penting untuk memastikan akurasi diagnosis dan untuk menghindari diagnosis yang salah.
- Pemantauan lingkungan: Ketidakpastian dalam pengukuran variabel lingkungan, seperti tingkat polusi udara atau air, dapat memengaruhi penilaian dampak lingkungan. Pertimbangan ketidakpastian ini penting untuk membuat keputusan yang tepat terkait dengan pengelolaan lingkungan.
Contoh Kasus Ketidakpastian Pengukuran Berulang dalam Bidang Lain
Berikut adalah beberapa contoh kasus di bidang lain yang melibatkan perhitungan ketidakpastian pengukuran berulang:
- Pengukuran ketinggian gunung: Dalam pengukuran ketinggian gunung, ketidakpastian dalam pengukuran ketinggian titik-titik referensi dan dalam penggunaan alat ukur dapat memengaruhi hasil akhir. Dengan mempertimbangkan ketidakpastian ini, para ahli dapat menentukan rentang ketinggian yang mungkin untuk gunung tersebut.
- Pengukuran kadar gula darah: Dalam pengukuran kadar gula darah, ketidakpastian dalam pengukuran sampel darah dan dalam penggunaan alat ukur dapat memengaruhi hasil akhir. Dengan mempertimbangkan ketidakpastian ini, para profesional kesehatan dapat menentukan rentang kadar gula darah yang normal dan mendeteksi potensi masalah kesehatan.
- Pengukuran tingkat polusi udara: Dalam pengukuran tingkat polusi udara, ketidakpastian dalam pengukuran konsentrasi polutan dan dalam penggunaan alat ukur dapat memengaruhi hasil akhir. Dengan mempertimbangkan ketidakpastian ini, para ahli lingkungan dapat menentukan tingkat polusi udara yang aman dan membuat keputusan yang tepat terkait dengan pengelolaan lingkungan.
Pengaruh Ketidakpastian Pengukuran Berulang pada Hasil dan Interpretasi
Ketidakpastian pengukuran berulang dapat memengaruhi hasil dan interpretasi dalam berbagai bidang dengan cara berikut:
- Akurasi hasil: Ketidakpastian dalam pengukuran dapat menyebabkan kesalahan dalam hasil akhir. Semakin besar ketidakpastian, semakin rendah akurasi hasil.
- Tingkat kepercayaan: Ketidakpastian dalam pengukuran memengaruhi tingkat kepercayaan pada hasil. Semakin kecil ketidakpastian, semakin tinggi tingkat kepercayaan pada hasil.
- Kesimpulan dan interpretasi: Ketidakpastian dalam pengukuran dapat memengaruhi kesimpulan dan interpretasi yang dibuat berdasarkan hasil. Pertimbangan ketidakpastian ini penting untuk menghindari kesimpulan yang salah dan untuk membuat interpretasi yang valid.
Ulasan Penutup
Memahami konsep ketidakpastian pengukuran berulang merupakan langkah penting dalam meningkatkan kualitas penelitian dan analisis data. Dengan memahami sumber-sumber ketidakpastian dan cara menghitungnya, kita dapat memperoleh hasil pengukuran yang lebih akurat dan menafsirkannya dengan lebih tepat. Hal ini penting dalam berbagai bidang, seperti fisika, kimia, biologi, dan teknik, untuk mencapai hasil penelitian yang valid dan dapat diandalkan.





