Menilai kemampuan siswa dalam matematika, khususnya melalui soal essay, bisa menjadi tantangan tersendiri bagi guru. Bagaimana memastikan penilaian objektif dan adil, sekaligus memberikan umpan balik yang bermanfaat bagi siswa? Jawabannya ada di dalam rubrik penilaian. Contoh Rubrik Penilaian Soal Essay Matematika menjadi alat yang praktis untuk membantu guru dalam proses penilaian yang lebih sistematis dan terstruktur.
Rubrik penilaian memberikan kerangka kerja yang jelas untuk menilai setiap aspek penting dalam jawaban essay matematika. Dari pemahaman konsep hingga kemampuan berpikir kritis, setiap komponen dinilai dengan standar yang terdefinisi, sehingga penilaian menjadi lebih adil dan transparan. Mari kita bahas lebih lanjut tentang contoh rubrik penilaian soal essay matematika dan manfaatnya dalam meningkatkan kualitas pembelajaran matematika.
Pengertian Rubrik Penilaian Soal Essay Matematika
Rubrik penilaian soal essay matematika adalah alat yang digunakan untuk menilai jawaban siswa secara objektif dan sistematis. Rubrik ini berisi kriteria penilaian yang jelas dan terstruktur, sehingga memudahkan guru dalam memberikan skor dan memberikan umpan balik yang lebih efektif kepada siswa.
Contoh Rubrik Penilaian Soal Essay Matematika
Berikut ini adalah contoh rubrik penilaian soal essay matematika yang sederhana:
| Kriteria | Skor | Keterangan |
|---|---|---|
| Ketepatan Jawaban | 4 | Jawaban benar dan tepat, menunjukkan pemahaman konsep yang mendalam. |
| 3 | Jawaban benar, tetapi terdapat sedikit kesalahan dalam perhitungan atau penyelesaian. | |
| 2 | Jawaban sebagian benar, menunjukkan pemahaman konsep yang kurang. | |
| 1 | Jawaban salah atau tidak relevan dengan pertanyaan. | |
| 0 | Tidak menjawab. | |
| Kelengkapan Jawaban | 2 | Jawaban lengkap dan terstruktur, menunjukkan langkah-langkah penyelesaian yang jelas. |
| 1 | Jawaban kurang lengkap, tetapi langkah-langkah penyelesaian masih terlihat. | |
| 0 | Jawaban tidak lengkap atau tidak terstruktur. | |
| Kejelasan Penjelasan | 2 | Penjelasan yang jelas dan mudah dipahami, menggunakan bahasa yang tepat dan logis. |
| 1 | Penjelasan kurang jelas, tetapi masih dapat dipahami. | |
| 0 | Penjelasan tidak jelas atau tidak logis. |
Manfaat Menggunakan Rubrik Penilaian Soal Essay Matematika
Ada beberapa manfaat yang bisa didapatkan dengan menggunakan rubrik penilaian soal essay matematika, yaitu:
- Meningkatkan Objektivitas Penilaian: Rubrik penilaian memberikan standar penilaian yang jelas dan terstruktur, sehingga mengurangi bias dalam penilaian dan meningkatkan objektivitasnya.
- Memudahkan Proses Penilaian: Rubrik penilaian membantu guru dalam memberikan skor secara cepat dan efisien, karena kriteria penilaian sudah terdefinisi dengan baik.
- Memberikan Umpan Balik yang Lebih Efektif: Rubrik penilaian membantu guru dalam memberikan umpan balik yang lebih spesifik dan terarah kepada siswa, karena kriteria penilaian yang jelas membantu guru dalam mengidentifikasi kekuatan dan kelemahan siswa.
- Meningkatkan Kualitas Pembelajaran: Rubrik penilaian dapat digunakan sebagai alat untuk meningkatkan kualitas pembelajaran, karena siswa dapat mengetahui kriteria penilaian yang diharapkan dari mereka.
Komponen Rubrik Penilaian Soal Essay Matematika: Contoh Rubrik Penilaian Soal Essay Matematika
Rubrik penilaian merupakan alat bantu yang sangat berguna dalam menilai jawaban essay matematika. Rubrik ini tidak hanya membantu guru dalam menilai jawaban siswa secara objektif dan adil, tetapi juga membantu siswa memahami kriteria yang digunakan dalam penilaian dan bagaimana mereka dapat meningkatkan kualitas jawaban mereka. Rubrik yang baik harus mencakup komponen-komponen utama yang mencerminkan aspek penting dalam jawaban essay matematika.
Komponen Utama Rubrik Penilaian Soal Essay Matematika
Komponen utama dalam rubrik penilaian soal essay matematika terdiri dari beberapa aspek penting yang mencerminkan kualitas jawaban siswa. Berikut adalah komponen-komponen utama tersebut:
- Pemahaman Konsep: Komponen ini menilai seberapa baik siswa memahami konsep matematika yang diujikan dalam soal. Ini meliputi kemampuan siswa untuk menjelaskan konsep dengan benar, menggunakan istilah matematika yang tepat, dan menghubungkan konsep dengan contoh-contoh yang relevan.
- Proses Penyelesaian: Komponen ini menilai bagaimana siswa menyelesaikan masalah matematika. Ini meliputi kemampuan siswa untuk menunjukkan langkah-langkah penyelesaian yang logis, menggunakan rumus dan teorema yang tepat, dan menunjukkan semua perhitungan yang diperlukan.
- Keakuratan: Komponen ini menilai keakuratan jawaban siswa. Ini meliputi kemampuan siswa untuk mendapatkan hasil yang benar, menunjukkan semua langkah perhitungan dengan benar, dan menghindari kesalahan konseptual atau perhitungan.
- Komunikasi Matematika: Komponen ini menilai bagaimana siswa mengkomunikasikan jawaban mereka secara jelas dan ringkas. Ini meliputi kemampuan siswa untuk menulis jawaban dengan bahasa matematika yang benar, menggunakan notasi matematika yang tepat, dan menyajikan jawaban secara terstruktur dan mudah dipahami.
Contoh Tabel Rubrik Penilaian Soal Essay Matematika
Berikut adalah contoh tabel rubrik penilaian soal essay matematika yang merinci komponen-komponen utama dan deskripsi singkatnya:
| Komponen | Sangat Baik (4) | Baik (3) | Cukup (2) | Kurang (1) |
|---|---|---|---|---|
| Pemahaman Konsep | Menunjukkan pemahaman yang mendalam tentang konsep matematika yang diujikan, mampu menjelaskan konsep dengan tepat dan memberikan contoh-contoh yang relevan. | Menunjukkan pemahaman yang cukup baik tentang konsep matematika yang diujikan, mampu menjelaskan konsep dengan cukup tepat, namun contoh-contoh yang diberikan kurang relevan. | Menunjukkan pemahaman yang terbatas tentang konsep matematika yang diujikan, penjelasan konsep kurang tepat dan contoh-contoh yang diberikan tidak relevan. | Tidak menunjukkan pemahaman tentang konsep matematika yang diujikan, penjelasan konsep tidak tepat dan contoh-contoh yang diberikan tidak relevan. |
| Proses Penyelesaian | Menunjukkan langkah-langkah penyelesaian yang logis, menggunakan rumus dan teorema yang tepat, dan menunjukkan semua perhitungan yang diperlukan dengan jelas dan terstruktur. | Menunjukkan langkah-langkah penyelesaian yang cukup logis, menggunakan rumus dan teorema yang tepat, namun beberapa perhitungan tidak ditunjukkan dengan jelas atau terstruktur. | Menunjukkan langkah-langkah penyelesaian yang kurang logis, menggunakan rumus dan teorema yang kurang tepat, dan beberapa perhitungan tidak ditunjukkan dengan jelas atau terstruktur. | Tidak menunjukkan langkah-langkah penyelesaian yang logis, menggunakan rumus dan teorema yang tidak tepat, dan perhitungan tidak ditunjukkan dengan jelas atau terstruktur. |
| Keakuratan | Menunjukkan hasil yang benar, semua langkah perhitungan ditunjukkan dengan benar, dan bebas dari kesalahan konseptual atau perhitungan. | Menunjukkan hasil yang benar, namun beberapa langkah perhitungan tidak ditunjukkan dengan benar, atau terdapat kesalahan konseptual atau perhitungan minor. | Menunjukkan hasil yang kurang tepat, beberapa langkah perhitungan tidak ditunjukkan dengan benar, atau terdapat kesalahan konseptual atau perhitungan yang signifikan. | Menunjukkan hasil yang salah, langkah-langkah perhitungan tidak ditunjukkan dengan benar, atau terdapat kesalahan konseptual atau perhitungan yang sangat signifikan. |
| Komunikasi Matematika | Menulis jawaban dengan bahasa matematika yang benar, menggunakan notasi matematika yang tepat, dan menyajikan jawaban secara terstruktur dan mudah dipahami. | Menulis jawaban dengan bahasa matematika yang cukup benar, menggunakan notasi matematika yang cukup tepat, dan menyajikan jawaban dengan struktur yang cukup baik. | Menulis jawaban dengan bahasa matematika yang kurang tepat, menggunakan notasi matematika yang kurang tepat, dan menyajikan jawaban dengan struktur yang kurang baik. | Menulis jawaban dengan bahasa matematika yang tidak tepat, menggunakan notasi matematika yang tidak tepat, dan menyajikan jawaban dengan struktur yang tidak baik. |
Manfaat Komponen Rubrik dalam Menilai Kualitas Jawaban Essay Matematika
Setiap komponen dalam rubrik penilaian memiliki peran penting dalam menilai kualitas jawaban essay matematika. Berikut adalah penjelasan singkat tentang bagaimana setiap komponen rubrik dapat membantu menilai kualitas jawaban essay matematika:
- Pemahaman Konsep: Komponen ini membantu menilai seberapa dalam pemahaman siswa tentang konsep matematika yang diujikan. Dengan memahami konsep dengan baik, siswa dapat menerapkannya dengan tepat dalam menyelesaikan masalah.
- Proses Penyelesaian: Komponen ini membantu menilai kemampuan siswa dalam mengaplikasikan konsep matematika yang dipahami untuk menyelesaikan masalah. Proses penyelesaian yang logis dan terstruktur menunjukkan bahwa siswa memiliki kemampuan berpikir kritis dan analitis dalam menyelesaikan masalah matematika.
- Keakuratan: Komponen ini membantu menilai kemampuan siswa dalam melakukan perhitungan matematika dengan benar. Keakuratan dalam perhitungan sangat penting untuk mendapatkan hasil yang benar dan valid.
- Komunikasi Matematika: Komponen ini membantu menilai kemampuan siswa dalam mengkomunikasikan jawaban mereka dengan jelas dan ringkas. Kemampuan berkomunikasi matematika yang baik menunjukkan bahwa siswa dapat menyampaikan ide dan hasil perhitungan mereka dengan tepat dan mudah dipahami oleh orang lain.
Tingkat Penilaian dalam Rubrik
Rubrik penilaian adalah alat yang sangat berguna untuk menilai tugas-tugas yang bersifat subjektif, seperti esai matematika. Rubrik ini memberikan kriteria penilaian yang jelas dan terstruktur, sehingga memudahkan guru dalam memberikan nilai yang adil dan objektif. Salah satu elemen penting dalam rubrik adalah tingkatan penilaian. Tingkatan penilaian ini membantu guru dalam membedakan kualitas jawaban siswa dengan lebih spesifik.
Tingkatan Penilaian dalam Rubrik
Tingkatan penilaian dalam rubrik biasanya terdiri dari beberapa level, seperti “Sangat Baik”, “Baik”, “Cukup”, dan “Kurang”. Setiap level mewakili rentang kemampuan dan kualitas jawaban siswa yang berbeda. Tingkatan penilaian ini berfungsi sebagai panduan untuk guru dalam memberikan nilai, dan juga membantu siswa dalam memahami apa yang diharapkan dari mereka dalam tugas tersebut.
Contoh Deskripsi Tingkatan Penilaian
- Sangat Baik: Jawaban siswa menunjukkan pemahaman yang mendalam tentang konsep yang diujikan. Jawabannya lengkap, akurat, dan didukung dengan contoh yang relevan. Penyelesaian masalah ditunjukkan dengan langkah-langkah yang jelas dan logis. Penulisan jawaban juga menunjukkan kemampuan siswa dalam mengorganisir ide dengan baik dan menggunakan bahasa yang tepat.
- Baik: Jawaban siswa menunjukkan pemahaman yang baik tentang konsep yang diujikan. Jawabannya lengkap dan akurat, tetapi mungkin kurang rinci atau contoh yang diberikan kurang relevan. Penyelesaian masalah ditunjukkan dengan langkah-langkah yang jelas, tetapi mungkin kurang logis. Penulisan jawaban menunjukkan kemampuan siswa dalam mengorganisir ide dengan baik, tetapi mungkin masih ada beberapa kekurangan dalam penggunaan bahasa.
- Cukup: Jawaban siswa menunjukkan pemahaman yang terbatas tentang konsep yang diujikan. Jawabannya mungkin tidak lengkap atau akurat. Penyelesaian masalah mungkin kurang jelas atau logis. Penulisan jawaban menunjukkan kemampuan siswa dalam mengorganisir ide, tetapi masih banyak kekurangan dalam penggunaan bahasa.
- Kurang: Jawaban siswa menunjukkan pemahaman yang sangat terbatas tentang konsep yang diujikan. Jawabannya tidak lengkap dan tidak akurat. Penyelesaian masalah tidak jelas dan tidak logis. Penulisan jawaban menunjukkan kekurangan dalam kemampuan siswa dalam mengorganisir ide dan menggunakan bahasa yang tepat.
Menentukan Skor untuk Setiap Tingkatan Penilaian
Setelah menentukan tingkatan penilaian, langkah selanjutnya adalah menentukan skor untuk setiap tingkatan. Skor ini dapat berupa angka, huruf, atau simbol lainnya. Penentuan skor harus mempertimbangkan bobot setiap kriteria penilaian dalam rubrik. Misalnya, jika kriteria “kejelasan jawaban” memiliki bobot yang lebih tinggi dibandingkan dengan kriteria “ketepatan jawaban”, maka skor untuk tingkatan penilaian yang tinggi pada kriteria “kejelasan jawaban” akan lebih tinggi dibandingkan dengan skor untuk tingkatan penilaian yang tinggi pada kriteria “ketepatan jawaban”.
Sebagai contoh, dalam rubrik penilaian untuk esai matematika, skor untuk tingkatan penilaian “Sangat Baik” pada kriteria “kejelasan jawaban” mungkin diberikan nilai 5, sedangkan skor untuk tingkatan penilaian “Sangat Baik” pada kriteria “ketepatan jawaban” mungkin diberikan nilai 4. Penentuan skor ini harus dilakukan secara konsisten dan adil untuk semua siswa.
Contoh Rubrik Penilaian Soal Essay Matematika Berdasarkan Tingkat Kesulitan
Rubrik penilaian soal essay matematika adalah alat yang sangat membantu guru dalam menilai kemampuan siswa dalam memecahkan masalah matematika. Rubrik ini memberikan kriteria yang jelas dan terstruktur untuk menilai setiap aspek jawaban siswa, sehingga penilaian menjadi lebih objektif dan adil. Dalam rubrik penilaian, tingkat kesulitan soal menjadi faktor penting yang perlu dipertimbangkan. Soal essay matematika dapat dikategorikan menjadi tiga tingkat kesulitan, yaitu mudah, sedang, dan sulit.
Tingkat kesulitan soal mempengaruhi rumusan soal, langkah penyelesaian, dan kriteria penilaian yang digunakan. Berikut ini contoh rubrik penilaian soal essay matematika berdasarkan tingkat kesulitan:
Soal Essay Matematika Tingkat Kesulitan Mudah
Soal essay matematika tingkat kesulitan mudah biasanya menguji pemahaman konsep dasar dan kemampuan siswa dalam menerapkan konsep tersebut pada soal sederhana. Soal ini biasanya terdiri dari satu langkah penyelesaian dan tidak memerlukan langkah-langkah kompleks.
| Kriteria | Skor | Keterangan |
|---|---|---|
| Ketepatan Jawaban | 4 | Jawaban benar dan lengkap, menunjukkan pemahaman konsep yang kuat. |
| 3 | Jawaban benar tetapi tidak lengkap, atau terdapat sedikit kesalahan dalam perhitungan. | |
| 2 | Jawaban sebagian benar, menunjukkan pemahaman konsep yang kurang. | |
| 1 | Jawaban salah, menunjukkan ketidakpahaman konsep. | |
| 0 | Tidak menjawab. | |
| Penyelesaian | 4 | Langkah-langkah penyelesaian benar dan lengkap, menunjukkan pemahaman konsep yang kuat. |
| 3 | Langkah-langkah penyelesaian benar tetapi tidak lengkap, atau terdapat sedikit kesalahan dalam perhitungan. | |
| 2 | Langkah-langkah penyelesaian sebagian benar, menunjukkan pemahaman konsep yang kurang. | |
| 1 | Langkah-langkah penyelesaian salah, menunjukkan ketidakpahaman konsep. | |
| 0 | Tidak menjawab. | |
| Kejelasan Penjelasan | 4 | Penjelasan jawaban jelas, logis, dan mudah dipahami. |
| 3 | Penjelasan jawaban kurang jelas, tetapi masih dapat dipahami. | |
| 2 | Penjelasan jawaban tidak jelas dan sulit dipahami. | |
| 1 | Tidak ada penjelasan. | |
| 0 | Tidak menjawab. |
Soal Essay Matematika Tingkat Kesulitan Sedang
Soal essay matematika tingkat kesulitan sedang menguji kemampuan siswa dalam menggabungkan beberapa konsep dan menerapkannya pada soal yang lebih kompleks. Soal ini biasanya terdiri dari beberapa langkah penyelesaian yang memerlukan pemahaman konsep yang lebih mendalam.
| Kriteria | Skor | Keterangan |
|---|---|---|
| Ketepatan Jawaban | 4 | Jawaban benar dan lengkap, menunjukkan pemahaman konsep yang kuat. |
| 3 | Jawaban benar tetapi tidak lengkap, atau terdapat sedikit kesalahan dalam perhitungan. | |
| 2 | Jawaban sebagian benar, menunjukkan pemahaman konsep yang kurang. | |
| 1 | Jawaban salah, menunjukkan ketidakpahaman konsep. | |
| 0 | Tidak menjawab. | |
| Penyelesaian | 4 | Langkah-langkah penyelesaian benar dan lengkap, menunjukkan pemahaman konsep yang kuat. |
| 3 | Langkah-langkah penyelesaian benar tetapi tidak lengkap, atau terdapat sedikit kesalahan dalam perhitungan. | |
| 2 | Langkah-langkah penyelesaian sebagian benar, menunjukkan pemahaman konsep yang kurang. | |
| 1 | Langkah-langkah penyelesaian salah, menunjukkan ketidakpahaman konsep. | |
| 0 | Tidak menjawab. | |
| Kejelasan Penjelasan | 4 | Penjelasan jawaban jelas, logis, dan mudah dipahami. |
| 3 | Penjelasan jawaban kurang jelas, tetapi masih dapat dipahami. | |
| 2 | Penjelasan jawaban tidak jelas dan sulit dipahami. | |
| 1 | Tidak ada penjelasan. | |
| 0 | Tidak menjawab. |
Soal Essay Matematika Tingkat Kesulitan Sulit
Soal essay matematika tingkat kesulitan sulit menguji kemampuan siswa dalam mengintegrasikan berbagai konsep dan menerapkannya pada soal yang kompleks dan menantang. Soal ini biasanya memerlukan analisis yang mendalam, strategi penyelesaian yang kreatif, dan pemahaman konsep yang komprehensif.
| Kriteria | Skor | Keterangan |
|---|---|---|
| Ketepatan Jawaban | 4 | Jawaban benar dan lengkap, menunjukkan pemahaman konsep yang kuat dan kemampuan analisis yang baik. |
| 3 | Jawaban benar tetapi tidak lengkap, atau terdapat sedikit kesalahan dalam perhitungan, menunjukkan pemahaman konsep yang kurang. | |
| 2 | Jawaban sebagian benar, menunjukkan pemahaman konsep yang kurang dan kemampuan analisis yang lemah. | |
| 1 | Jawaban salah, menunjukkan ketidakpahaman konsep dan ketidakmampuan dalam menganalisis soal. | |
| 0 | Tidak menjawab. | |
| Penyelesaian | 4 | Langkah-langkah penyelesaian benar dan lengkap, menunjukkan pemahaman konsep yang kuat dan kemampuan analisis yang baik. |
| 3 | Langkah-langkah penyelesaian benar tetapi tidak lengkap, atau terdapat sedikit kesalahan dalam perhitungan, menunjukkan pemahaman konsep yang kurang. | |
| 2 | Langkah-langkah penyelesaian sebagian benar, menunjukkan pemahaman konsep yang kurang dan kemampuan analisis yang lemah. | |
| 1 | Langkah-langkah penyelesaian salah, menunjukkan ketidakpahaman konsep dan ketidakmampuan dalam menganalisis soal. | |
| 0 | Tidak menjawab. | |
| Kejelasan Penjelasan | 4 | Penjelasan jawaban jelas, logis, dan mudah dipahami, menunjukkan kemampuan komunikasi matematika yang baik. |
| 3 | Penjelasan jawaban kurang jelas, tetapi masih dapat dipahami, menunjukkan kemampuan komunikasi matematika yang kurang. | |
| 2 | Penjelasan jawaban tidak jelas dan sulit dipahami, menunjukkan kemampuan komunikasi matematika yang lemah. | |
| 1 | Tidak ada penjelasan, menunjukkan ketidakmampuan dalam mengkomunikasikan jawaban. | |
| 0 | Tidak menjawab. |
Contoh Rubrik Penilaian Soal Essay Matematika Berdasarkan Topik
Rubrik penilaian merupakan panduan yang sangat penting dalam menilai soal essay matematika. Dengan rubrik, penilaian akan lebih objektif, adil, dan konsisten. Rubrik juga membantu siswa memahami kriteria yang digunakan dalam penilaian sehingga mereka dapat belajar lebih efektif. Berikut ini adalah contoh rubrik penilaian untuk soal essay matematika berdasarkan topik.
Aljabar
Rubrik penilaian untuk soal essay matematika tentang aljabar biasanya mencakup aspek-aspek seperti pemahaman konsep, kemampuan menyelesaikan persamaan dan pertidaksamaan, kemampuan mengaplikasikan konsep aljabar dalam masalah kontekstual, dan kemampuan menyajikan solusi dengan jelas dan benar.
| Kriteria | Skor | Keterangan |
|---|---|---|
| Pemahaman Konsep | 4 | Siswa menunjukkan pemahaman yang mendalam tentang konsep aljabar yang diuji dan dapat menjelaskan konsep tersebut dengan benar. |
| Pemahaman Konsep | 3 | Siswa menunjukkan pemahaman yang baik tentang konsep aljabar yang diuji, tetapi mungkin terdapat sedikit kesalahan dalam penjelasan. |
| Pemahaman Konsep | 2 | Siswa menunjukkan pemahaman yang terbatas tentang konsep aljabar yang diuji. |
| Pemahaman Konsep | 1 | Siswa tidak menunjukkan pemahaman tentang konsep aljabar yang diuji. |
| Kemampuan Menyelesaikan Persamaan dan Pertidaksamaan | 4 | Siswa dapat menyelesaikan persamaan dan pertidaksamaan dengan benar dan menunjukkan langkah-langkah penyelesaian yang jelas dan logis. |
| Kemampuan Menyelesaikan Persamaan dan Pertidaksamaan | 3 | Siswa dapat menyelesaikan persamaan dan pertidaksamaan dengan benar, tetapi mungkin terdapat sedikit kesalahan dalam langkah-langkah penyelesaian. |
| Kemampuan Menyelesaikan Persamaan dan Pertidaksamaan | 2 | Siswa mengalami kesulitan dalam menyelesaikan persamaan dan pertidaksamaan. |
| Kemampuan Menyelesaikan Persamaan dan Pertidaksamaan | 1 | Siswa tidak dapat menyelesaikan persamaan dan pertidaksamaan. |
| Kemampuan Mengaplikasikan Konsep Aljabar dalam Masalah Kontekstual | 4 | Siswa dapat menerapkan konsep aljabar dalam masalah kontekstual dengan tepat dan menunjukkan pemahaman yang mendalam tentang masalah tersebut. |
| Kemampuan Mengaplikasikan Konsep Aljabar dalam Masalah Kontekstual | 3 | Siswa dapat menerapkan konsep aljabar dalam masalah kontekstual dengan cukup tepat, tetapi mungkin terdapat sedikit kesalahan dalam penerapannya. |
| Kemampuan Mengaplikasikan Konsep Aljabar dalam Masalah Kontekstual | 2 | Siswa mengalami kesulitan dalam menerapkan konsep aljabar dalam masalah kontekstual. |
| Kemampuan Mengaplikasikan Konsep Aljabar dalam Masalah Kontekstual | 1 | Siswa tidak dapat menerapkan konsep aljabar dalam masalah kontekstual. |
| Kemampuan Menyajikan Solusi dengan Jelas dan Benar | 4 | Siswa menyajikan solusi dengan jelas, terstruktur, dan mudah dipahami. Solusi juga benar dan lengkap. |
| Kemampuan Menyajikan Solusi dengan Jelas dan Benar | 3 | Siswa menyajikan solusi dengan cukup jelas, tetapi mungkin terdapat sedikit kesalahan dalam penyajian. |
| Kemampuan Menyajikan Solusi dengan Jelas dan Benar | 2 | Siswa mengalami kesulitan dalam menyajikan solusi dengan jelas dan benar. |
| Kemampuan Menyajikan Solusi dengan Jelas dan Benar | 1 | Siswa tidak dapat menyajikan solusi dengan jelas dan benar. |
Geometri
Rubrik penilaian untuk soal essay matematika tentang geometri biasanya mencakup aspek-aspek seperti pemahaman konsep, kemampuan mengidentifikasi dan menganalisis bangun ruang dan datar, kemampuan menyelesaikan masalah geometri dengan menggunakan rumus dan teorema, dan kemampuan menyajikan solusi dengan jelas dan benar.
| Kriteria | Skor | Keterangan |
|---|---|---|
| Pemahaman Konsep | 4 | Siswa menunjukkan pemahaman yang mendalam tentang konsep geometri yang diuji dan dapat menjelaskan konsep tersebut dengan benar. |
| Pemahaman Konsep | 3 | Siswa menunjukkan pemahaman yang baik tentang konsep geometri yang diuji, tetapi mungkin terdapat sedikit kesalahan dalam penjelasan. |
| Pemahaman Konsep | 2 | Siswa menunjukkan pemahaman yang terbatas tentang konsep geometri yang diuji. |
| Pemahaman Konsep | 1 | Siswa tidak menunjukkan pemahaman tentang konsep geometri yang diuji. |
| Kemampuan Mengidentifikasi dan Menganalisis Bangun Ruang dan Datar | 4 | Siswa dapat mengidentifikasi dan menganalisis bangun ruang dan datar dengan benar dan menunjukkan pemahaman yang mendalam tentang sifat-sifat bangun tersebut. |
| Kemampuan Mengidentifikasi dan Menganalisis Bangun Ruang dan Datar | 3 | Siswa dapat mengidentifikasi dan menganalisis bangun ruang dan datar dengan cukup tepat, tetapi mungkin terdapat sedikit kesalahan dalam identifikasi atau analisis. |
| Kemampuan Mengidentifikasi dan Menganalisis Bangun Ruang dan Datar | 2 | Siswa mengalami kesulitan dalam mengidentifikasi dan menganalisis bangun ruang dan datar. |
| Kemampuan Mengidentifikasi dan Menganalisis Bangun Ruang dan Datar | 1 | Siswa tidak dapat mengidentifikasi dan menganalisis bangun ruang dan datar. |
| Kemampuan Menyelesaikan Masalah Geometri dengan Menggunakan Rumus dan Teorema | 4 | Siswa dapat menyelesaikan masalah geometri dengan benar dan menunjukkan langkah-langkah penyelesaian yang jelas dan logis. Siswa juga dapat memilih dan menerapkan rumus dan teorema yang tepat. |
| Kemampuan Menyelesaikan Masalah Geometri dengan Menggunakan Rumus dan Teorema | 3 | Siswa dapat menyelesaikan masalah geometri dengan benar, tetapi mungkin terdapat sedikit kesalahan dalam langkah-langkah penyelesaian atau pemilihan rumus dan teorema. |
| Kemampuan Menyelesaikan Masalah Geometri dengan Menggunakan Rumus dan Teorema | 2 | Siswa mengalami kesulitan dalam menyelesaikan masalah geometri. |
| Kemampuan Menyelesaikan Masalah Geometri dengan Menggunakan Rumus dan Teorema | 1 | Siswa tidak dapat menyelesaikan masalah geometri. |
| Kemampuan Menyajikan Solusi dengan Jelas dan Benar | 4 | Siswa menyajikan solusi dengan jelas, terstruktur, dan mudah dipahami. Solusi juga benar dan lengkap. |
| Kemampuan Menyajikan Solusi dengan Jelas dan Benar | 3 | Siswa menyajikan solusi dengan cukup jelas, tetapi mungkin terdapat sedikit kesalahan dalam penyajian. |
| Kemampuan Menyajikan Solusi dengan Jelas dan Benar | 2 | Siswa mengalami kesulitan dalam menyajikan solusi dengan jelas dan benar. |
| Kemampuan Menyajikan Solusi dengan Jelas dan Benar | 1 | Siswa tidak dapat menyajikan solusi dengan jelas dan benar. |
Statistika
Rubrik penilaian untuk soal essay matematika tentang statistika biasanya mencakup aspek-aspek seperti pemahaman konsep, kemampuan mengumpulkan, mengolah, dan menganalisis data, kemampuan menginterpretasikan hasil analisis data, dan kemampuan menyajikan hasil analisis data dengan jelas dan benar.
Contoh rubrik penilaian soal essay matematika bisa jadi agak rumit, ya. Soalnya, kita perlu menilai lebih dari sekadar jawaban yang benar. Misalnya, kalau soal essaynya tentang pertumbuhan penduduk geometrik, kita bisa lihat bagaimana siswa menganalisis dan menghitungnya. Nah, untuk menemukan contoh soal pertumbuhan penduduk geometrik yang menarik, bisa dicek di situs ini.
Setelah itu, kamu bisa buat rubrik penilaian yang menilai kemampuan siswa dalam memahami konsep, menghitung, dan juga mengomunikasikan jawabannya dengan jelas.
| Kriteria | Skor | Keterangan |
|---|---|---|
| Pemahaman Konsep | 4 | Siswa menunjukkan pemahaman yang mendalam tentang konsep statistika yang diuji dan dapat menjelaskan konsep tersebut dengan benar. |
| Pemahaman Konsep | 3 | Siswa menunjukkan pemahaman yang baik tentang konsep statistika yang diuji, tetapi mungkin terdapat sedikit kesalahan dalam penjelasan. |
| Pemahaman Konsep | 2 | Siswa menunjukkan pemahaman yang terbatas tentang konsep statistika yang diuji. |
| Pemahaman Konsep | 1 | Siswa tidak menunjukkan pemahaman tentang konsep statistika yang diuji. |
| Kemampuan Mengumpulkan, Mengolah, dan Menganalisis Data | 4 | Siswa dapat mengumpulkan, mengolah, dan menganalisis data dengan benar dan menunjukkan pemahaman yang mendalam tentang metode statistika yang digunakan. |
| Kemampuan Mengumpulkan, Mengolah, dan Menganalisis Data | 3 | Siswa dapat mengumpulkan, mengolah, dan menganalisis data dengan cukup tepat, tetapi mungkin terdapat sedikit kesalahan dalam proses pengumpulan, pengolahan, atau analisis. |
| Kemampuan Mengumpulkan, Mengolah, dan Menganalisis Data | 2 | Siswa mengalami kesulitan dalam mengumpulkan, mengolah, dan menganalisis data. |
| Kemampuan Mengumpulkan, Mengolah, dan Menganalisis Data | 1 | Siswa tidak dapat mengumpulkan, mengolah, dan menganalisis data. |
| Kemampuan Menginterpretasikan Hasil Analisis Data | 4 | Siswa dapat menginterpretasikan hasil analisis data dengan benar dan menunjukkan pemahaman yang mendalam tentang makna hasil tersebut. |
| Kemampuan Menginterpretasikan Hasil Analisis Data | 3 | Siswa dapat menginterpretasikan hasil analisis data dengan cukup tepat, tetapi mungkin terdapat sedikit kesalahan dalam interpretasi. |
| Kemampuan Menginterpretasikan Hasil Analisis Data | 2 | Siswa mengalami kesulitan dalam menginterpretasikan hasil analisis data. |
| Kemampuan Menginterpretasikan Hasil Analisis Data | 1 | Siswa tidak dapat menginterpretasikan hasil analisis data. |
| Kemampuan Menyajikan Hasil Analisis Data dengan Jelas dan Benar | 4 | Siswa menyajikan hasil analisis data dengan jelas, terstruktur, dan mudah dipahami. Penyajian juga benar dan lengkap. |
| Kemampuan Menyajikan Hasil Analisis Data dengan Jelas dan Benar | 3 | Siswa menyajikan hasil analisis data dengan cukup jelas, tetapi mungkin terdapat sedikit kesalahan dalam penyajian. |
| Kemampuan Menyajikan Hasil Analisis Data dengan Jelas dan Benar | 2 | Siswa mengalami kesulitan dalam menyajikan hasil analisis data dengan jelas dan benar. |
| Kemampuan Menyajikan Hasil Analisis Data dengan Jelas dan Benar | 1 | Siswa tidak dapat menyajikan hasil analisis data dengan jelas dan benar. |
Tips Menyusun Rubrik Penilaian Soal Essay Matematika
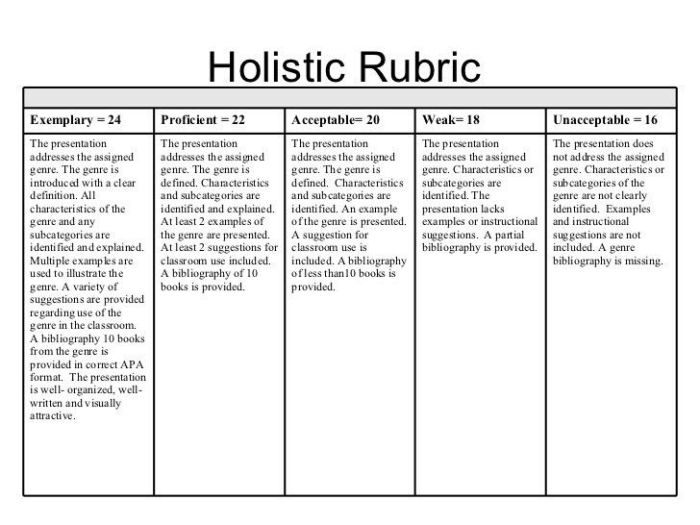
Rubrik penilaian soal essay matematika merupakan alat yang penting untuk menilai kemampuan siswa dalam memecahkan masalah dan mengomunikasikan pemikiran matematis mereka. Rubrik yang baik akan membantu guru untuk menilai secara adil dan objektif, serta memberikan umpan balik yang konstruktif kepada siswa.
Menentukan Kriteria Penilaian
Langkah pertama dalam menyusun rubrik penilaian soal essay matematika adalah menentukan kriteria penilaian yang ingin dinilai. Kriteria ini harus relevan dengan tujuan pembelajaran dan tingkat kesulitan soal. Berikut beberapa contoh kriteria yang dapat digunakan:
- Kemampuan memahami konsep matematika
- Kemampuan menyelesaikan masalah matematika
- Kemampuan mengomunikasikan pemikiran matematis dengan jelas dan logis
- Kemampuan menggunakan bahasa matematika yang benar
- Kemampuan menyajikan jawaban dengan rapi dan teratur
Menentukan Tingkat Penilaian
Setelah menentukan kriteria penilaian, langkah selanjutnya adalah menentukan tingkat penilaian untuk setiap kriteria. Tingkat penilaian ini dapat berupa skala numerik, seperti 1-4 atau 1-5, atau skala deskriptif, seperti “Sangat Baik”, “Baik”, “Cukup”, dan “Kurang”.
Tingkat penilaian harus mencerminkan tingkat kemampuan siswa dalam memenuhi kriteria. Misalnya, tingkat penilaian “Sangat Baik” diberikan kepada siswa yang mampu memenuhi semua kriteria dengan sangat baik, sedangkan tingkat penilaian “Kurang” diberikan kepada siswa yang tidak memenuhi sebagian besar kriteria.
Membuat Contoh Rubrik
Berikut contoh rubrik penilaian untuk soal essay matematika yang membahas tentang persamaan linear:
| Kriteria | Sangat Baik | Baik | Cukup | Kurang |
|---|---|---|---|---|
| Memahami konsep persamaan linear | Siswa dapat menjelaskan konsep persamaan linear dengan benar dan memberikan contoh yang tepat. | Siswa dapat menjelaskan konsep persamaan linear dengan benar, tetapi contoh yang diberikan kurang tepat. | Siswa dapat menjelaskan konsep persamaan linear dengan kurang tepat. | Siswa tidak dapat menjelaskan konsep persamaan linear. |
| Menyelesaikan masalah persamaan linear | Siswa dapat menyelesaikan masalah persamaan linear dengan benar dan menunjukkan langkah-langkah penyelesaian yang tepat. | Siswa dapat menyelesaikan masalah persamaan linear dengan benar, tetapi langkah-langkah penyelesaian yang ditunjukkan kurang tepat. | Siswa dapat menyelesaikan masalah persamaan linear dengan kurang tepat. | Siswa tidak dapat menyelesaikan masalah persamaan linear. |
| Mengomunikasikan pemikiran matematis dengan jelas dan logis | Siswa dapat mengomunikasikan pemikiran matematis dengan jelas dan logis, serta menggunakan bahasa matematika yang benar. | Siswa dapat mengomunikasikan pemikiran matematis dengan jelas dan logis, tetapi penggunaan bahasa matematika kurang tepat. | Siswa dapat mengomunikasikan pemikiran matematis dengan kurang jelas dan logis. | Siswa tidak dapat mengomunikasikan pemikiran matematis dengan jelas dan logis. |
| Menyajikan jawaban dengan rapi dan teratur | Siswa menyajikan jawaban dengan rapi dan teratur, serta menggunakan notasi matematika yang benar. | Siswa menyajikan jawaban dengan rapi dan teratur, tetapi penggunaan notasi matematika kurang tepat. | Siswa menyajikan jawaban dengan kurang rapi dan teratur. | Siswa menyajikan jawaban dengan tidak rapi dan tidak teratur. |
Menyesuaikan Rubrik dengan Tujuan Pembelajaran dan Tingkat Kesulitan Soal
Rubrik penilaian harus disesuaikan dengan tujuan pembelajaran dan tingkat kesulitan soal. Jika tujuan pembelajaran adalah untuk menguji kemampuan siswa dalam menyelesaikan masalah matematika yang kompleks, maka rubrik harus lebih fokus pada kriteria yang mengukur kemampuan tersebut. Sebaliknya, jika tujuan pembelajaran adalah untuk menguji kemampuan siswa dalam memahami konsep matematika dasar, maka rubrik harus lebih fokus pada kriteria yang mengukur kemampuan tersebut.
Tingkat kesulitan soal juga harus dipertimbangkan dalam menyusun rubrik penilaian. Jika soal essay matematika sangat sulit, maka tingkat penilaian harus lebih rendah. Sebaliknya, jika soal essay matematika mudah, maka tingkat penilaian harus lebih tinggi.
Tips Menyusun Rubrik Penilaian Soal Essay Matematika
Berikut beberapa tips untuk menyusun rubrik penilaian soal essay matematika yang efektif:
- Tentukan kriteria penilaian yang jelas dan spesifik.
- Buat tingkat penilaian yang mudah dipahami dan diinterpretasikan.
- Berikan contoh jawaban untuk setiap tingkat penilaian.
- Uji coba rubrik penilaian dengan soal essay matematika yang serupa.
- Revisi rubrik penilaian berdasarkan hasil uji coba.
Kelebihan dan Kekurangan Rubrik Penilaian Soal Essay Matematika
Rubrik penilaian merupakan alat yang efektif untuk menilai hasil belajar siswa dalam bentuk essay matematika. Rubrik ini memberikan panduan yang jelas dan terstruktur dalam menentukan skor dan menilai kualitas jawaban siswa. Namun, seperti halnya alat penilaian lainnya, rubrik juga memiliki kelebihan dan kekurangan.
Kelebihan Rubrik Penilaian Soal Essay Matematika
Penggunaan rubrik penilaian soal essay matematika memiliki beberapa kelebihan, antara lain:
- Meningkatkan Objektivitas Penilaian: Rubrik membantu mengurangi bias subjektivitas dalam penilaian. Dengan kriteria penilaian yang jelas dan terstruktur, guru dapat menilai jawaban siswa secara objektif, mengurangi pengaruh faktor personal dalam penilaian.
- Meningkatkan Konsistensi Penilaian: Rubrik membantu guru dalam menilai jawaban siswa secara konsisten, baik untuk satu kelas maupun antar kelas. Dengan menggunakan kriteria yang sama, guru dapat memberikan nilai yang adil dan objektif kepada semua siswa.
- Memberikan Umpan Balik yang Lebih Bermakna: Rubrik membantu guru dalam memberikan umpan balik yang lebih bermakna kepada siswa. Dengan melihat kriteria penilaian yang tercantum dalam rubrik, siswa dapat memahami apa yang mereka lakukan dengan baik dan apa yang perlu diperbaiki.
- Meningkatkan Keterlibatan Siswa: Rubrik dapat membantu meningkatkan keterlibatan siswa dalam proses belajar. Dengan mengetahui kriteria penilaian, siswa dapat lebih fokus pada aspek-aspek penting yang perlu dipenuhi dalam menjawab soal essay.
Kekurangan Rubrik Penilaian Soal Essay Matematika
Meskipun memiliki banyak kelebihan, rubrik penilaian soal essay matematika juga memiliki beberapa kekurangan, yaitu:
- Membutuhkan Waktu dan Usaha Ekstra: Membuat rubrik yang baik dan efektif membutuhkan waktu dan usaha ekstra dari guru. Guru harus merumuskan kriteria penilaian yang jelas, terstruktur, dan relevan dengan tujuan pembelajaran.
- Sulit Menilai Aspek Kreativitas dan Keaslian: Rubrik seringkali berfokus pada aspek-aspek teknis dan procedural dalam menjawab soal essay, sehingga sulit untuk menilai aspek kreativitas dan keaslian dalam jawaban siswa.
- Kurang Fleksibel dalam Menilai Jawaban yang Unik: Rubrik yang terlalu rigid dapat menghambat guru dalam menilai jawaban siswa yang unik dan tidak terduga. Rubrik yang terlalu ketat dapat mengabaikan aspek-aspek penting yang tidak tercantum dalam kriteria penilaian.
Mengatasi Kekurangan Rubrik Penilaian Soal Essay Matematika
- Rubrik yang Fleksibel: Guru dapat membuat rubrik yang lebih fleksibel dengan menyertakan kriteria penilaian yang terbuka dan tidak terlalu rigid. Guru dapat memberikan ruang bagi siswa untuk menunjukkan kreativitas dan keaslian dalam menjawab soal essay.
- Penilaian Tambahan: Guru dapat menggunakan metode penilaian tambahan untuk menilai aspek-aspek yang tidak tercakup dalam rubrik, seperti kreativitas, keaslian, dan kemampuan berpikir kritis. Contohnya, guru dapat memberikan pertanyaan tambahan yang menuntut siswa untuk menunjukkan pemahaman konsep secara lebih mendalam.
- Diskusi dan Refleksi: Guru dapat melakukan diskusi dan refleksi bersama siswa setelah penilaian dilakukan. Diskusi ini dapat membantu siswa memahami kriteria penilaian dan bagaimana mereka dapat meningkatkan kualitas jawaban mereka di masa depan.
Penerapan Rubrik Penilaian Soal Essay Matematika dalam Praktik
Rubrik penilaian adalah alat yang sangat berguna untuk menilai soal essay matematika. Rubrik memberikan panduan yang jelas dan objektif dalam menilai jawaban siswa, sehingga penilaian menjadi lebih adil dan konsisten. Selain itu, rubrik juga dapat membantu siswa memahami kriteria yang diharapkan dalam menjawab soal essay.
Cara Menerapkan Rubrik Penilaian Soal Essay Matematika dalam Praktik
Penerapan rubrik penilaian soal essay matematika dalam praktik dapat dilakukan dengan beberapa langkah berikut:
- Buat rubrik penilaian yang jelas dan detail. Rubrik harus mencakup semua aspek yang ingin dinilai dalam jawaban essay, seperti pemahaman konsep, proses penyelesaian, keakuratan, dan penyajian.
- Berikan rubrik kepada siswa sebelum mereka mengerjakan soal essay. Hal ini akan membantu siswa memahami apa yang diharapkan dari mereka dan bagaimana jawaban mereka akan dinilai.
- Gunakan rubrik sebagai panduan dalam menilai jawaban essay. Bacalah setiap jawaban essay dengan cermat dan gunakan rubrik untuk menilai setiap aspek jawaban.
- Berikan umpan balik kepada siswa berdasarkan rubrik. Jelaskan kepada siswa apa yang mereka lakukan dengan baik dan apa yang perlu mereka tingkatkan. Gunakan rubrik sebagai dasar untuk memberikan umpan balik yang spesifik dan konstruktif.
Contoh Cara Menggunakan Rubrik untuk Menilai Jawaban Essay Matematika
Berikut ini adalah contoh rubrik penilaian untuk soal essay matematika yang membahas tentang persamaan linear:
| Kriteria | Skor 4 | Skor 3 | Skor 2 | Skor 1 |
|---|---|---|---|---|
| Pemahaman Konsep | Siswa menunjukkan pemahaman yang mendalam tentang konsep persamaan linear dan mampu menerapkannya dengan tepat dalam menyelesaikan masalah. | Siswa menunjukkan pemahaman yang cukup tentang konsep persamaan linear, namun masih terdapat beberapa kesalahan dalam penerapannya. | Siswa menunjukkan pemahaman yang terbatas tentang konsep persamaan linear, dan terdapat banyak kesalahan dalam penerapannya. | Siswa tidak menunjukkan pemahaman tentang konsep persamaan linear. |
| Proses Penyelesaian | Siswa menunjukkan langkah-langkah penyelesaian yang benar dan terstruktur dengan baik. | Siswa menunjukkan langkah-langkah penyelesaian yang sebagian besar benar, namun terdapat beberapa kesalahan atau kurang terstruktur. | Siswa menunjukkan langkah-langkah penyelesaian yang sebagian besar salah atau tidak terstruktur. | Siswa tidak menunjukkan langkah-langkah penyelesaian. |
| Keakuratan | Semua jawaban benar dan akurat. | Sebagian besar jawaban benar dan akurat, namun terdapat beberapa kesalahan. | Sebagian besar jawaban salah atau tidak akurat. | Semua jawaban salah atau tidak akurat. |
| Penyajian | Jawaban disajikan dengan jelas, ringkas, dan mudah dipahami. | Jawaban disajikan dengan cukup jelas, namun kurang ringkas atau mudah dipahami. | Jawaban disajikan dengan tidak jelas dan sulit dipahami. | Jawaban tidak disajikan dengan baik. |
Contoh soal essay: “Tentukan solusi dari persamaan linear 2x + 3 = 7.” Berdasarkan rubrik di atas, jawaban siswa dapat dinilai dengan menggunakan tabel rubrik sebagai panduan. Misalnya, jika siswa menunjukkan langkah-langkah penyelesaian yang benar dan akurat, namun kurang terstruktur dalam penyajiannya, maka skor yang diberikan adalah 3 untuk kriteria “Proses Penyelesaian” dan 2 untuk kriteria “Penyajian”.
Contoh Cara Memberikan Umpan Balik kepada Siswa Berdasarkan Rubrik Penilaian, Contoh rubrik penilaian soal essay matematika
Umpan balik yang diberikan kepada siswa harus spesifik, konstruktif, dan berdasarkan pada rubrik penilaian. Misalnya, jika siswa mendapatkan skor 2 untuk kriteria “Pemahaman Konsep”, maka umpan balik yang diberikan dapat berupa:
“Kamu menunjukkan pemahaman yang terbatas tentang konsep persamaan linear. Kamu masih kesulitan dalam menerapkan konsep ini untuk menyelesaikan masalah. Silahkan pelajari kembali materi tentang persamaan linear dan berlatihlah dengan mengerjakan soal-soal latihan.”
Dengan memberikan umpan balik yang spesifik dan konstruktif, siswa dapat memahami apa yang perlu mereka tingkatkan dan bagaimana mereka dapat meningkatkan pemahaman mereka tentang konsep matematika.
Kesimpulan dan Saran
Pembahasan tentang rubrik penilaian soal essay matematika telah menjelaskan bagaimana rubrik dapat membantu guru dalam menilai hasil belajar siswa secara objektif, adil, dan konsisten. Rubrik juga dapat membantu siswa memahami kriteria penilaian dan meningkatkan kualitas penulisan jawaban essay mereka.
Poin-Poin Penting
Rubrik penilaian soal essay matematika memiliki beberapa poin penting yang perlu diingat:
- Rubrik harus jelas, ringkas, dan mudah dipahami oleh guru dan siswa.
- Rubrik harus mencakup semua aspek penting yang ingin dinilai dalam soal essay.
- Rubrik harus menggunakan bahasa yang mudah dipahami dan menghindari istilah teknis yang tidak familiar.
- Rubrik harus fleksibel dan dapat disesuaikan dengan kebutuhan pembelajaran.
Saran untuk Meningkatkan Kualitas Rubrik
Untuk meningkatkan kualitas rubrik penilaian soal essay matematika, beberapa saran dapat diterapkan:
- Berkolaborasi dengan guru lain untuk mengembangkan rubrik yang komprehensif dan efektif.
- Melakukan uji coba rubrik dengan siswa dan mendapatkan umpan balik untuk perbaikan.
- Memperbarui rubrik secara berkala agar tetap relevan dengan kurikulum dan kebutuhan pembelajaran.
- Menggunakan teknologi untuk membantu dalam proses penilaian dan analisis data.
Pentingnya Menggunakan Rubrik Penilaian
Penggunaan rubrik penilaian dalam proses pembelajaran matematika memiliki beberapa manfaat penting:
- Meningkatkan objektivitas dan konsistensi penilaian.
- Membantu siswa memahami kriteria penilaian dan meningkatkan kualitas jawaban essay.
- Memudahkan guru dalam memberikan umpan balik yang spesifik dan konstruktif.
- Meningkatkan transparansi dan akuntabilitas dalam proses penilaian.
Simpulan Akhir
Dengan menggunakan contoh rubrik penilaian soal essay matematika, guru dapat meningkatkan kualitas penilaian dan memberikan umpan balik yang lebih efektif kepada siswa. Rubrik bukan hanya alat untuk menilai, tetapi juga untuk membimbing siswa dalam memahami konsep matematika dengan lebih baik. Melalui rubrik yang terstruktur, proses pembelajaran matematika menjadi lebih bermakna dan membantu siswa mencapai potensi optimalnya.





