Contoh soal bangun ruang sisi datar – Pernahkah kamu membayangkan bagaimana menghitung luas permukaan kotak kado atau volume bak mandi? Nah, di situlah konsep bangun ruang sisi datar berperan! Bangun ruang sisi datar merupakan objek tiga dimensi yang dibatasi oleh sisi-sisi datar, seperti kubus, balok, prisma, dan limas. Mempelajari bangun ruang sisi datar tidak hanya melatih kemampuan berpikir spasial, tetapi juga bermanfaat dalam berbagai bidang kehidupan, mulai dari arsitektur hingga teknologi.
Dalam artikel ini, kita akan menjelajahi berbagai jenis bangun ruang sisi datar, rumus-rumus pentingnya, serta contoh soal yang menantang. Siap-siap untuk mengasah kemampuanmu dalam memecahkan masalah geometri dan mengaplikasikannya dalam kehidupan nyata!
Pengertian Bangun Ruang Sisi Datar
Bangun ruang sisi datar merupakan bangun tiga dimensi yang dibatasi oleh beberapa sisi datar. Bangun ruang ini memiliki volume dan luas permukaan. Bayangkan sebuah kotak, lemari, atau bahkan sebuah rumah. Semuanya adalah contoh dari bangun ruang sisi datar. Nah, di artikel ini kita akan membahas lebih dalam tentang bangun ruang sisi datar, mulai dari pengertian hingga contohnya dalam kehidupan sehari-hari.
Pengertian Bangun Ruang Sisi Datar
Bangun ruang sisi datar adalah bangun tiga dimensi yang dibatasi oleh sisi-sisi yang berbentuk bidang datar. Sisi-sisi ini saling berpotongan membentuk rusuk dan titik sudut. Bangun ruang sisi datar memiliki volume dan luas permukaan. Volume merupakan ukuran ruang yang ditempati oleh bangun ruang, sedangkan luas permukaan merupakan jumlah luas semua sisi yang membatasi bangun ruang.
Contoh Bangun Ruang Sisi Datar dalam Kehidupan Sehari-hari
Banyak sekali contoh bangun ruang sisi datar yang kita jumpai dalam kehidupan sehari-hari. Berikut beberapa contohnya:
- Kubus: Kotak mainan, dadu, rubik.
- Balok: Lemari, buku, meja.
- Prisma: Tabung pasta gigi, pensil, atap rumah.
- Limas: Piramida, tenda, atap rumah dengan bentuk segitiga.
Perbedaan Bangun Ruang Sisi Datar dengan Bangun Datar
Berikut tabel yang membandingkan ciri-ciri bangun ruang sisi datar dengan bangun datar:
| Ciri | Bangun Ruang Sisi Datar | Bangun Datar |
|---|---|---|
| Dimensi | Tiga dimensi (panjang, lebar, tinggi) | Dua dimensi (panjang, lebar) |
| Sisi | Memiliki sisi-sisi yang berbentuk bidang datar | Memiliki sisi-sisi yang berbentuk garis lurus |
| Rusuk | Memiliki rusuk yang merupakan garis potong antar sisi | Memiliki sisi yang merupakan garis lurus |
| Titik Sudut | Memiliki titik sudut yang merupakan titik potong antar rusuk | Memiliki titik sudut yang merupakan titik potong antar sisi |
| Volume | Memiliki volume | Tidak memiliki volume |
| Luas Permukaan | Memiliki luas permukaan | Memiliki luas |
Jenis-jenis Bangun Ruang Sisi Datar: Contoh Soal Bangun Ruang Sisi Datar
Bangun ruang sisi datar adalah bangun ruang yang dibatasi oleh sisi-sisi yang berbentuk bidang datar. Bangun ruang ini memiliki volume dan luas permukaan. Ada beberapa jenis bangun ruang sisi datar yang umum dipelajari, yaitu kubus, balok, prisma, limas, dan tabung. Setiap jenis bangun ruang sisi datar memiliki ciri khas dan rumus perhitungan yang berbeda. Mari kita bahas satu per satu!
Kubus
Kubus adalah bangun ruang sisi datar yang memiliki enam sisi berbentuk persegi yang sama besar dan sejajar. Semua rusuk kubus memiliki panjang yang sama. Kubus juga memiliki 12 rusuk dan 8 titik sudut.
- Contoh Soal: Sebuah kubus memiliki panjang rusuk 5 cm. Hitunglah volume dan luas permukaan kubus tersebut!
- Ilustrasi: Bayangkan sebuah kotak mainan yang memiliki semua sisinya berbentuk persegi dan memiliki ukuran yang sama. Itulah contoh dari kubus. Setiap sisi kotak tersebut adalah sisi kubus, dan setiap sudut kotak adalah titik sudut kubus.
Balok
Balok adalah bangun ruang sisi datar yang memiliki enam sisi berbentuk persegi panjang. Balok memiliki tiga pasang sisi yang sejajar dan sama besar. Balok memiliki 12 rusuk dan 8 titik sudut.
- Contoh Soal: Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 8 cm. Hitunglah volume dan luas permukaan balok tersebut!
- Ilustrasi: Bayangkan sebuah kotak sepatu. Kotak sepatu memiliki enam sisi berbentuk persegi panjang, dan setiap sisi memiliki ukuran yang berbeda. Itulah contoh dari balok. Setiap sisi kotak sepatu adalah sisi balok, dan setiap sudut kotak sepatu adalah titik sudut balok.
Prisma
Prisma adalah bangun ruang sisi datar yang memiliki dua sisi sejajar dan kongruen yang disebut alas dan tutup, serta sisi-sisi tegak yang berbentuk persegi panjang. Prisma dibedakan berdasarkan bentuk alasnya, seperti prisma segitiga, prisma persegi, prisma segilima, dan seterusnya.
- Contoh Soal: Sebuah prisma segitiga memiliki alas berbentuk segitiga sama sisi dengan panjang sisi 6 cm. Tinggi prisma adalah 10 cm. Hitunglah volume dan luas permukaan prisma tersebut!
- Ilustrasi: Bayangkan sebuah potongan keju yang berbentuk segitiga. Jika Anda menumpuk beberapa potongan keju segitiga tersebut, Anda akan mendapatkan sebuah prisma segitiga. Setiap potongan keju adalah alas dan tutup prisma, dan setiap sisi keju yang tegak adalah sisi tegak prisma.
Limas
Limas adalah bangun ruang sisi datar yang memiliki alas berbentuk poligon dan sisi-sisi tegak berbentuk segitiga yang bertemu pada satu titik yang disebut puncak. Limas dibedakan berdasarkan bentuk alasnya, seperti limas segitiga, limas persegi, limas segilima, dan seterusnya.
- Contoh Soal: Sebuah limas persegi memiliki alas berbentuk persegi dengan panjang sisi 8 cm. Tinggi limas adalah 12 cm. Hitunglah volume dan luas permukaan limas tersebut!
- Ilustrasi: Bayangkan sebuah piramida. Piramida memiliki alas berbentuk persegi dan sisi-sisi tegak berbentuk segitiga yang bertemu pada satu titik di puncak. Itulah contoh dari limas persegi. Setiap sisi segitiga adalah sisi tegak limas, dan alas piramida adalah alas limas.
Tabung
Tabung adalah bangun ruang sisi datar yang memiliki dua sisi sejajar dan kongruen yang disebut alas dan tutup, serta sisi lengkung yang disebut selimut tabung. Alas dan tutup tabung berbentuk lingkaran.
- Contoh Soal: Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 15 cm. Hitunglah volume dan luas permukaan tabung tersebut!
- Ilustrasi: Bayangkan sebuah kaleng susu. Kaleng susu memiliki dua sisi berbentuk lingkaran yang sejajar dan satu sisi lengkung yang mengelilingi kedua lingkaran tersebut. Itulah contoh dari tabung. Kedua lingkaran adalah alas dan tutup tabung, dan sisi lengkung adalah selimut tabung.
Rumus dan Sifat Bangun Ruang Sisi Datar
Bangun ruang sisi datar adalah bangun ruang yang seluruh permukaannya dibatasi oleh bidang datar. Bangun ruang sisi datar memiliki berbagai bentuk dan sifat yang unik, dan masing-masing memiliki rumus khusus untuk menghitung luas permukaan dan volumenya. Mari kita bahas lebih detail mengenai rumus dan sifat dari beberapa bangun ruang sisi datar yang umum.
Kubus
Kubus adalah bangun ruang sisi datar yang memiliki enam sisi berbentuk persegi yang sama besar dan kongruen. Semua rusuknya memiliki panjang yang sama, dan semua sudutnya merupakan sudut siku-siku. Berikut adalah rumus dan sifat kubus:
- Rumus Luas Permukaan: 6s2, di mana s adalah panjang rusuk kubus.
- Rumus Volume: s3, di mana s adalah panjang rusuk kubus.
- Sifat-sifat Kubus:
- Memiliki 6 sisi berbentuk persegi yang sama besar dan kongruen.
- Memiliki 12 rusuk yang sama panjang.
- Memiliki 8 titik sudut yang sama besar.
- Semua sudutnya adalah sudut siku-siku.
- Diagonal sisi kubus memiliki panjang s√2.
- Diagonal ruang kubus memiliki panjang s√3.
Balok
Balok adalah bangun ruang sisi datar yang memiliki enam sisi berbentuk persegi panjang. Balok memiliki tiga pasang sisi yang berhadapan dan kongruen. Berikut adalah rumus dan sifat balok:
- Rumus Luas Permukaan: 2(pl + pt + lt), di mana p adalah panjang, l adalah lebar, dan t adalah tinggi balok.
- Rumus Volume: p x l x t, di mana p adalah panjang, l adalah lebar, dan t adalah tinggi balok.
- Sifat-sifat Balok:
- Memiliki 6 sisi berbentuk persegi panjang.
- Memiliki 12 rusuk yang tidak semuanya sama panjang.
- Memiliki 8 titik sudut yang sama besar.
- Semua sudutnya adalah sudut siku-siku.
- Diagonal sisi balok memiliki panjang √(p2 + l2).
- Diagonal ruang balok memiliki panjang √(p2 + l2 + t2).
Prisma Segitiga
Prisma segitiga adalah bangun ruang sisi datar yang memiliki dua sisi berbentuk segitiga yang kongruen dan sejajar, dan tiga sisi berbentuk persegi panjang. Berikut adalah rumus dan sifat prisma segitiga:
- Rumus Luas Permukaan: 2 x Luas Alas + Luas Sisi Tegak, di mana Luas Alas adalah luas segitiga dan Luas Sisi Tegak adalah luas persegi panjang.
- Rumus Volume: Luas Alas x Tinggi, di mana Luas Alas adalah luas segitiga dan Tinggi adalah jarak antara dua sisi segitiga yang sejajar.
- Sifat-sifat Prisma Segitiga:
- Memiliki 5 sisi, yaitu 2 sisi berbentuk segitiga dan 3 sisi berbentuk persegi panjang.
- Memiliki 9 rusuk.
- Memiliki 6 titik sudut.
- Sisi-sisi yang berhadapan sejajar dan kongruen.
Limas Segi Empat
Limas segi empat adalah bangun ruang sisi datar yang memiliki alas berbentuk segi empat dan empat sisi berbentuk segitiga yang bertemu pada satu titik puncak. Berikut adalah rumus dan sifat limas segi empat:
- Rumus Luas Permukaan: Luas Alas + Luas Sisi Tegak, di mana Luas Alas adalah luas segi empat dan Luas Sisi Tegak adalah jumlah luas keempat segitiga.
- Rumus Volume: 1/3 x Luas Alas x Tinggi, di mana Luas Alas adalah luas segi empat dan Tinggi adalah jarak dari puncak limas ke bidang alas.
- Sifat-sifat Limas Segi Empat:
- Memiliki 5 sisi, yaitu 1 sisi berbentuk segi empat dan 4 sisi berbentuk segitiga.
- Memiliki 8 rusuk.
- Memiliki 5 titik sudut.
- Semua sisi tegak bertemu pada satu titik puncak.
Kerucut
Kerucut adalah bangun ruang sisi datar yang memiliki alas berbentuk lingkaran dan sisi tegak berbentuk lengkung yang bertemu pada satu titik puncak. Berikut adalah rumus dan sifat kerucut:
- Rumus Luas Permukaan: πr2 + πrs, di mana r adalah jari-jari lingkaran alas dan s adalah garis pelukis kerucut.
- Rumus Volume: 1/3πr2t, di mana r adalah jari-jari lingkaran alas dan t adalah tinggi kerucut.
- Sifat-sifat Kerucut:
- Memiliki 2 sisi, yaitu 1 sisi berbentuk lingkaran dan 1 sisi berbentuk lengkung.
- Memiliki 1 rusuk.
- Memiliki 1 titik sudut.
- Semua titik pada sisi lengkung bertemu pada satu titik puncak.
Tabung
Tabung adalah bangun ruang sisi datar yang memiliki dua sisi berbentuk lingkaran yang kongruen dan sejajar, dan satu sisi berbentuk lengkung yang menghubungkan kedua lingkaran tersebut. Berikut adalah rumus dan sifat tabung:
- Rumus Luas Permukaan: 2πr2 + 2πrt, di mana r adalah jari-jari lingkaran alas dan t adalah tinggi tabung.
- Rumus Volume: πr2t, di mana r adalah jari-jari lingkaran alas dan t adalah tinggi tabung.
- Sifat-sifat Tabung:
- Memiliki 3 sisi, yaitu 2 sisi berbentuk lingkaran dan 1 sisi berbentuk lengkung.
- Memiliki 2 rusuk.
- Memiliki 0 titik sudut.
- Sisi-sisi yang berhadapan sejajar dan kongruen.
Bola, Contoh soal bangun ruang sisi datar
Bola adalah bangun ruang sisi datar yang memiliki permukaan yang melengkung dan semua titik pada permukaannya berjarak sama dari titik pusatnya. Berikut adalah rumus dan sifat bola:
- Rumus Luas Permukaan: 4πr2, di mana r adalah jari-jari bola.
- Rumus Volume: 4/3πr3, di mana r adalah jari-jari bola.
- Sifat-sifat Bola:
- Memiliki 1 sisi berbentuk lengkung.
- Memiliki 0 rusuk.
- Memiliki 0 titik sudut.
- Semua titik pada permukaan bola berjarak sama dari titik pusatnya.
Tabel Rumus dan Sifat Bangun Ruang Sisi Datar
| Bangun Ruang | Rumus Luas Permukaan | Rumus Volume | Sifat-sifat |
|---|---|---|---|
| Kubus | 6s2 | s3 | – Memiliki 6 sisi berbentuk persegi yang sama besar dan kongruen. – Memiliki 12 rusuk yang sama panjang. – Memiliki 8 titik sudut yang sama besar. – Semua sudutnya adalah sudut siku-siku. – Diagonal sisi kubus memiliki panjang s√2. – Diagonal ruang kubus memiliki panjang s√3. |
| Balok | 2(pl + pt + lt) | p x l x t | – Memiliki 6 sisi berbentuk persegi panjang. – Memiliki 12 rusuk yang tidak semuanya sama panjang. – Memiliki 8 titik sudut yang sama besar. – Semua sudutnya adalah sudut siku-siku. – Diagonal sisi balok memiliki panjang √(p2 + l2). – Diagonal ruang balok memiliki panjang √(p2 + l2 + t2). |
| Prisma Segitiga | 2 x Luas Alas + Luas Sisi Tegak | Luas Alas x Tinggi | – Memiliki 5 sisi, yaitu 2 sisi berbentuk segitiga dan 3 sisi berbentuk persegi panjang. – Memiliki 9 rusuk. – Memiliki 6 titik sudut. – Sisi-sisi yang berhadapan sejajar dan kongruen. |
| Limas Segi Empat | Luas Alas + Luas Sisi Tegak | 1/3 x Luas Alas x Tinggi | – Memiliki 5 sisi, yaitu 1 sisi berbentuk segi empat dan 4 sisi berbentuk segitiga. – Memiliki 8 rusuk. – Memiliki 5 titik sudut. – Semua sisi tegak bertemu pada satu titik puncak. |
| Kerucut | πr2 + πrs | 1/3πr2t | – Memiliki 2 sisi, yaitu 1 sisi berbentuk lingkaran dan 1 sisi berbentuk lengkung. – Memiliki 1 rusuk. – Memiliki 1 titik sudut. – Semua titik pada sisi lengkung bertemu pada satu titik puncak. |
| Tabung | 2πr2 + 2πrt | πr2t | – Memiliki 3 sisi, yaitu 2 sisi berbentuk lingkaran dan 1 sisi berbentuk lengkung. – Memiliki 2 rusuk. – Memiliki 0 titik sudut. – Sisi-sisi yang berhadapan sejajar dan kongruen. |
| Bola | 4πr2 | 4/3πr3 | – Memiliki 1 sisi berbentuk lengkung. – Memiliki 0 rusuk. – Memiliki 0 titik sudut. – Semua titik pada permukaan bola berjarak sama dari titik pusatnya. |
Soal-soal Latihan Bangun Ruang Sisi Datar
Setelah mempelajari berbagai macam bangun ruang sisi datar, sekarang saatnya untuk menguji pemahamanmu dengan mengerjakan soal-soal latihan. Soal-soal ini akan mengasah kemampuanmu dalam menghitung luas permukaan dan volume bangun ruang sisi datar. Mari kita mulai!
Luas Permukaan Bangun Ruang Sisi Datar
Luas permukaan bangun ruang sisi datar adalah jumlah luas semua sisi bangun ruang tersebut. Untuk menghitung luas permukaan, kita perlu mengetahui rumus luas masing-masing sisi dan kemudian menjumlahkannya. Berikut adalah contoh soal latihan untuk menghitung luas permukaan bangun ruang sisi datar:
- Hitung luas permukaan kubus dengan panjang rusuk 5 cm.
- Sebuah balok memiliki panjang 8 cm, lebar 6 cm, dan tinggi 4 cm. Hitung luas permukaan balok tersebut.
- Hitung luas permukaan prisma segitiga dengan alas segitiga siku-siku yang memiliki panjang sisi alas 6 cm, tinggi 8 cm, dan sisi miring 10 cm. Tinggi prisma adalah 12 cm.
- Sebuah limas segitiga memiliki alas segitiga sama sisi dengan panjang sisi 10 cm. Tinggi limas adalah 12 cm. Hitung luas permukaan limas tersebut.
- Hitung luas permukaan kerucut dengan jari-jari alas 7 cm dan tinggi 24 cm.
Volume Bangun Ruang Sisi Datar
Volume bangun ruang sisi datar adalah ukuran ruang yang ditempati oleh bangun ruang tersebut. Untuk menghitung volume, kita perlu mengetahui rumus volume masing-masing bangun ruang. Berikut adalah contoh soal latihan untuk menghitung volume bangun ruang sisi datar:
- Hitung volume kubus dengan panjang rusuk 7 cm.
- Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 3 cm. Hitung volume balok tersebut.
- Hitung volume prisma segitiga dengan alas segitiga siku-siku yang memiliki panjang sisi alas 4 cm, tinggi 3 cm, dan sisi miring 5 cm. Tinggi prisma adalah 10 cm.
- Sebuah limas segitiga memiliki alas segitiga sama sisi dengan panjang sisi 6 cm. Tinggi limas adalah 8 cm. Hitung volume limas tersebut.
- Hitung volume kerucut dengan jari-jari alas 5 cm dan tinggi 12 cm.
Soal Cerita Bangun Ruang Sisi Datar
Soal cerita merupakan soal yang disajikan dalam bentuk cerita dan melibatkan konsep bangun ruang sisi datar. Soal cerita ini melatih kemampuan kita dalam memahami dan menerapkan konsep bangun ruang sisi datar dalam kehidupan sehari-hari. Berikut adalah contoh soal cerita yang melibatkan konsep bangun ruang sisi datar:
- Sebuah kotak kado berbentuk kubus dengan panjang rusuk 15 cm akan dibungkus dengan kertas kado. Berapa luas kertas kado yang dibutuhkan untuk membungkus kotak kado tersebut?
- Sebuah bak mandi berbentuk balok dengan panjang 1,5 meter, lebar 1 meter, dan tinggi 0,8 meter akan diisi air hingga penuh. Berapa liter air yang dibutuhkan untuk mengisi bak mandi tersebut?
- Sebuah tenda berbentuk limas segitiga dengan alas segitiga sama sisi dengan panjang sisi 3 meter dan tinggi tenda 2 meter. Berapa volume udara di dalam tenda tersebut?
Penerapan Bangun Ruang Sisi Datar dalam Kehidupan Sehari-hari
Bangun ruang sisi datar merupakan salah satu materi geometri yang dipelajari di sekolah. Materi ini mungkin tampak abstrak, namun sebenarnya memiliki banyak sekali penerapan dalam kehidupan sehari-hari. Bangun ruang sisi datar dapat kita temui di berbagai bidang, seperti arsitektur, industri, dan seni. Pembahasan ini akan mengulas beberapa contoh penerapan bangun ruang sisi datar dalam kehidupan sehari-hari, manfaat mempelajari materi ini, serta bagaimana materi ini dapat membantu kita dalam memecahkan masalah di dunia nyata.
Penerapan dalam Arsitektur
Arsitektur merupakan salah satu bidang yang paling banyak menggunakan konsep bangun ruang sisi datar. Bangunan-bangunan yang kita lihat di sekitar kita, mulai dari rumah, gedung perkantoran, hingga bangunan monumental, merupakan contoh nyata penerapan bangun ruang sisi datar.
- Rumah: Rumah merupakan contoh sederhana dari penerapan bangun ruang sisi datar. Bentuk rumah yang paling umum adalah bentuk kubus atau balok, yang terdiri dari sisi-sisi persegi panjang atau persegi. Rumah dengan bentuk limas juga dapat ditemukan, seperti rumah adat di beberapa daerah.
- Gedung Perkantoran: Gedung perkantoran biasanya memiliki bentuk yang lebih kompleks, namun tetap mengandalkan konsep bangun ruang sisi datar. Gedung-gedung ini seringkali menggunakan bentuk kubus, balok, prisma, dan limas untuk menciptakan ruang yang fungsional dan estetis.
- Bangunan Monumental: Bangunan monumental seperti museum, stadion, atau monumen, seringkali memiliki bentuk yang unik dan menarik. Bentuk-bentuk ini biasanya menggabungkan berbagai macam bangun ruang sisi datar untuk menciptakan efek visual yang dramatis.
Penerapan dalam Industri
Konsep bangun ruang sisi datar juga banyak diterapkan dalam industri. Bentuk-bentuk bangun ruang sisi datar digunakan dalam desain berbagai macam produk, mulai dari peralatan rumah tangga hingga mesin-mesin industri.
- Peralatan Rumah Tangga: Peralatan rumah tangga seperti kulkas, televisi, dan mesin cuci, seringkali menggunakan bentuk kubus, balok, atau silinder untuk memudahkan proses produksi dan penyimpanan.
- Mesin-mesin Industri: Mesin-mesin industri seperti mesin bubut, mesin frais, dan mesin bor, menggunakan berbagai macam bangun ruang sisi datar dalam desainnya. Bentuk-bentuk ini dipilih untuk menghasilkan produk yang presisi dan efisien.
- Kemasan Produk: Kemasan produk juga merupakan contoh penerapan bangun ruang sisi datar. Bentuk kemasan yang dipilih harus melindungi produk, mudah diangkut, dan menarik bagi konsumen.
Penerapan dalam Seni
Konsep bangun ruang sisi datar juga banyak digunakan dalam seni. Para seniman memanfaatkan bentuk-bentuk bangun ruang sisi datar untuk menciptakan karya seni yang indah dan menarik.
- Patung: Patung merupakan salah satu bentuk seni yang banyak menggunakan konsep bangun ruang sisi datar. Para pematung menggunakan bentuk-bentuk bangun ruang sisi datar untuk menciptakan bentuk patung yang realistis atau abstrak.
- Instalasi Seni: Instalasi seni seringkali menggunakan berbagai macam bangun ruang sisi datar untuk menciptakan efek visual yang menarik dan interaktif.
- Arsitektur Lanskap: Arsitektur lanskap juga memanfaatkan konsep bangun ruang sisi datar untuk menciptakan taman yang indah dan fungsional.
Manfaat Mempelajari Bangun Ruang Sisi Datar
Mempelajari bangun ruang sisi datar tidak hanya bermanfaat untuk memahami konsep geometri, tetapi juga memiliki manfaat praktis dalam kehidupan sehari-hari. Berikut adalah beberapa manfaat mempelajari bangun ruang sisi datar:
- Meningkatkan Kemampuan Spasial: Mempelajari bangun ruang sisi datar dapat meningkatkan kemampuan spasial, yaitu kemampuan untuk memahami dan memanipulasi bentuk dan ruang.
- Membantu dalam Memecahkan Masalah: Konsep bangun ruang sisi datar dapat digunakan untuk memecahkan masalah di berbagai bidang, seperti arsitektur, teknik, dan desain.
- Meningkatkan Kreativitas: Mempelajari bangun ruang sisi datar dapat meningkatkan kreativitas, karena kita dapat mengeksplorasi berbagai macam bentuk dan ruang.
Menghitung Luas Permukaan Bangun Ruang Sisi Datar
Luas permukaan bangun ruang sisi datar merupakan total luas dari semua sisi bangun ruang tersebut. Menghitung luas permukaan bangun ruang sisi datar sangat berguna dalam berbagai bidang, seperti arsitektur, desain, dan manufaktur.
Berikut adalah langkah-langkah umum untuk menghitung luas permukaan bangun ruang sisi datar:
Menghitung Luas Permukaan Kubus
Kubus adalah bangun ruang sisi datar yang memiliki enam sisi yang berbentuk persegi dan sama besar. Untuk menghitung luas permukaan kubus, kita dapat menggunakan rumus berikut:
Luas permukaan kubus = 6 x sisi x sisi
Berikut adalah contoh soal menghitung luas permukaan kubus:
- Sebuah kubus memiliki panjang sisi 5 cm. Hitunglah luas permukaan kubus tersebut!
Penyelesaian:
- Diketahui: sisi = 5 cm
- Ditanya: Luas permukaan kubus?
- Jawab: Luas permukaan kubus = 6 x sisi x sisi = 6 x 5 cm x 5 cm = 150 cm2
Jadi, luas permukaan kubus tersebut adalah 150 cm2.
Menghitung Luas Permukaan Balok
Balok adalah bangun ruang sisi datar yang memiliki enam sisi yang berbentuk persegi panjang. Untuk menghitung luas permukaan balok, kita dapat menggunakan rumus berikut:
Luas permukaan balok = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
Berikut adalah contoh soal menghitung luas permukaan balok:
- Sebuah balok memiliki panjang 8 cm, lebar 5 cm, dan tinggi 3 cm. Hitunglah luas permukaan balok tersebut!
Penyelesaian:
- Diketahui: panjang = 8 cm, lebar = 5 cm, tinggi = 3 cm
- Ditanya: Luas permukaan balok?
- Jawab: Luas permukaan balok = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi) = 2 x (8 cm x 5 cm + 8 cm x 3 cm + 5 cm x 3 cm) = 2 x (40 cm2 + 24 cm2 + 15 cm2) = 2 x 79 cm2 = 158 cm2
Jadi, luas permukaan balok tersebut adalah 158 cm2.
Contoh soal bangun ruang sisi datar, seperti menghitung volume kubus atau luas permukaan prisma, seringkali melibatkan perhitungan sederhana. Namun, menghitung volume limas atau luas permukaan kerucut bisa lebih kompleks. Untuk menyelesaikan soal-soal tersebut, terkadang kita membutuhkan pemahaman tentang konsep persamaan dan pertidaksamaan nilai mutlak linear satu variabel, yang bisa ditemukan di contoh soal persamaan dan pertidaksamaan nilai mutlak linear satu variabel.
Dengan menguasai materi ini, kita bisa lebih mudah dalam menyelesaikan soal-soal bangun ruang sisi datar yang lebih menantang.
Menghitung Luas Permukaan Prisma Segitiga
Prisma segitiga adalah bangun ruang sisi datar yang memiliki dua sisi berbentuk segitiga dan tiga sisi berbentuk persegi panjang. Untuk menghitung luas permukaan prisma segitiga, kita dapat menggunakan rumus berikut:
Luas permukaan prisma segitiga = 2 x luas alas + keliling alas x tinggi prisma
Berikut adalah contoh soal menghitung luas permukaan prisma segitiga:
- Sebuah prisma segitiga memiliki alas berbentuk segitiga siku-siku dengan panjang sisi alas 6 cm, sisi tinggi 8 cm, dan sisi miring 10 cm. Tinggi prisma tersebut adalah 12 cm. Hitunglah luas permukaan prisma segitiga tersebut!
Penyelesaian:
- Diketahui: alas segitiga = 6 cm, tinggi segitiga = 8 cm, sisi miring segitiga = 10 cm, tinggi prisma = 12 cm
- Ditanya: Luas permukaan prisma segitiga?
- Jawab: Luas alas segitiga = 1/2 x alas x tinggi = 1/2 x 6 cm x 8 cm = 24 cm2
- Keliling alas segitiga = alas + tinggi + sisi miring = 6 cm + 8 cm + 10 cm = 24 cm
- Luas permukaan prisma segitiga = 2 x luas alas + keliling alas x tinggi prisma = 2 x 24 cm2 + 24 cm x 12 cm = 48 cm2 + 288 cm2 = 336 cm2
Jadi, luas permukaan prisma segitiga tersebut adalah 336 cm2.
Menghitung Volume Bangun Ruang Sisi Datar
Volume bangun ruang sisi datar adalah ukuran ruang yang ditempati oleh bangun ruang tersebut. Untuk menghitung volume bangun ruang sisi datar, kita perlu mengetahui bentuk dan ukuran bangun ruang tersebut. Ada beberapa rumus yang dapat digunakan untuk menghitung volume bangun ruang sisi datar, tergantung pada bentuk bangun ruang tersebut. Rumus volume bangun ruang sisi datar ini berguna untuk menghitung berbagai hal, seperti kapasitas wadah, volume air dalam kolam renang, atau volume udara dalam ruangan.
Menghitung Volume Kubus
Kubus adalah bangun ruang sisi datar yang memiliki enam sisi yang berbentuk persegi dan semua sisinya sama panjang. Untuk menghitung volume kubus, kita dapat menggunakan rumus:
Volume kubus = sisi x sisi x sisi
Contoh soal:
- Sebuah kubus memiliki panjang sisi 5 cm. Berapakah volume kubus tersebut?
Penyelesaian:
- Diketahui: sisi = 5 cm
- Ditanya: volume kubus?
- Jawab: Volume kubus = sisi x sisi x sisi = 5 cm x 5 cm x 5 cm = 125 cm3
Jadi, volume kubus tersebut adalah 125 cm3.
Menghitung Volume Balok
Balok adalah bangun ruang sisi datar yang memiliki enam sisi yang berbentuk persegi panjang. Untuk menghitung volume balok, kita dapat menggunakan rumus:
Volume balok = panjang x lebar x tinggi
Contoh soal:
- Sebuah balok memiliki panjang 10 cm, lebar 5 cm, dan tinggi 3 cm. Berapakah volume balok tersebut?
Penyelesaian:
- Diketahui: panjang = 10 cm, lebar = 5 cm, tinggi = 3 cm
- Ditanya: volume balok?
- Jawab: Volume balok = panjang x lebar x tinggi = 10 cm x 5 cm x 3 cm = 150 cm3
Jadi, volume balok tersebut adalah 150 cm3.
Menghitung Volume Prisma Segitiga
Prisma segitiga adalah bangun ruang sisi datar yang memiliki dua sisi berbentuk segitiga dan tiga sisi berbentuk persegi panjang. Untuk menghitung volume prisma segitiga, kita dapat menggunakan rumus:
Volume prisma segitiga = luas alas x tinggi
Contoh soal:
- Sebuah prisma segitiga memiliki alas berbentuk segitiga siku-siku dengan panjang sisi alas 6 cm, tinggi alas 8 cm, dan tinggi prisma 10 cm. Berapakah volume prisma segitiga tersebut?
Penyelesaian:
- Diketahui: sisi alas = 6 cm, tinggi alas = 8 cm, tinggi prisma = 10 cm
- Ditanya: volume prisma segitiga?
- Jawab: Luas alas = 1/2 x alas x tinggi = 1/2 x 6 cm x 8 cm = 24 cm2
- Volume prisma segitiga = luas alas x tinggi = 24 cm2 x 10 cm = 240 cm3
Jadi, volume prisma segitiga tersebut adalah 240 cm3.
Soal-soal HOTS Bangun Ruang Sisi Datar
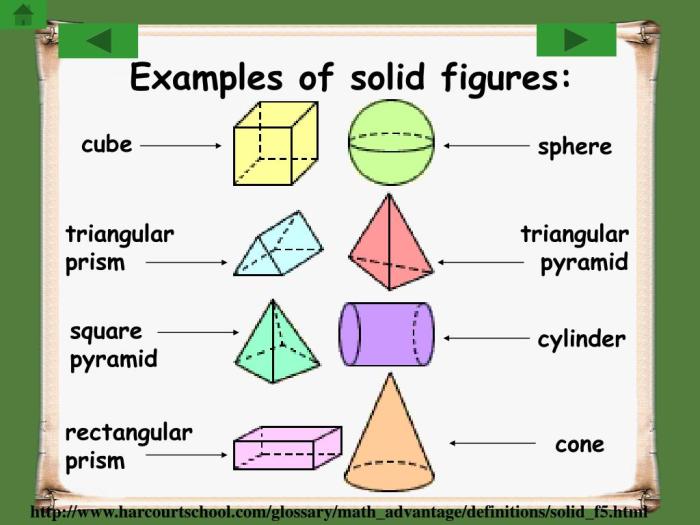
Soal HOTS (Higher Order Thinking Skills) dalam bangun ruang sisi datar dirancang untuk menguji kemampuan berpikir tingkat tinggi, seperti analisis, evaluasi, dan pemecahan masalah. Soal-soal ini menuntut siswa untuk memahami konsep dasar, menerapkannya dalam situasi yang lebih kompleks, dan menghubungkan konsep-konsep tersebut dengan kehidupan nyata.
Soal-soal HOTS
Berikut adalah contoh soal HOTS tentang bangun ruang sisi datar:
- Sebuah balok memiliki panjang, lebar, dan tinggi masing-masing 12 cm, 8 cm, dan 6 cm. Jika balok tersebut dipotong menjadi kubus-kubus kecil dengan panjang rusuk 2 cm, berapa banyak kubus kecil yang dapat dihasilkan?
- Sebuah limas segiempat beraturan memiliki alas persegi dengan panjang sisi 10 cm dan tinggi limas 12 cm. Titik A terletak di tengah salah satu sisi alas limas. Hitung jarak titik A ke puncak limas!
- Sebuah kerucut memiliki jari-jari alas 7 cm dan tinggi 24 cm. Jika kerucut tersebut dipotong menjadi dua bagian yang sama besar oleh bidang yang sejajar dengan alas dan jaraknya 8 cm dari alas, tentukan perbandingan volume kedua bagian kerucut tersebut!
Langkah-langkah Menyelesaikan Soal HOTS
Untuk menyelesaikan soal HOTS tentang bangun ruang sisi datar, ada beberapa langkah yang perlu diperhatikan:
- Memahami Konsep Dasar: Pastikan kamu memahami konsep-konsep dasar bangun ruang sisi datar seperti rumus luas permukaan, volume, dan sifat-sifat bangun ruang.
- Menganalisis Soal: Bacalah soal dengan cermat dan identifikasi informasi yang diberikan dan apa yang ditanyakan.
- Membuat Gambar: Jika memungkinkan, buatlah gambar bangun ruang yang sesuai dengan soal untuk membantu visualisasi.
- Menentukan Strategi Pemecahan: Pilih strategi yang tepat untuk menyelesaikan soal, seperti menggunakan rumus, teorema, atau metode lain yang relevan.
- Melakukan Perhitungan: Hitunglah dengan teliti dan pastikan langkah-langkah perhitungan benar.
- Menuliskan Jawaban: Tuliskan jawaban dengan lengkap dan jelas, serta sertakan satuan yang sesuai.
Contoh Jawaban dan Pembahasan
Berikut contoh jawaban dan pembahasan untuk soal HOTS nomor 1:
- Memahami Konsep Dasar: Untuk menentukan banyak kubus kecil yang dapat dihasilkan, kita perlu membagi volume balok dengan volume kubus kecil.
- Menganalisis Soal: Diketahui panjang, lebar, dan tinggi balok, serta panjang rusuk kubus kecil. Kita diminta untuk menentukan banyak kubus kecil yang dapat dihasilkan.
- Membuat Gambar: Gambar balok dan kubus kecil yang dipotong dari balok tersebut.
- Menentukan Strategi Pemecahan: Kita akan menggunakan rumus volume balok dan volume kubus untuk menentukan banyak kubus kecil yang dapat dihasilkan.
- Melakukan Perhitungan:
- Volume balok = panjang x lebar x tinggi = 12 cm x 8 cm x 6 cm = 576 cm3
- Volume kubus kecil = rusuk x rusuk x rusuk = 2 cm x 2 cm x 2 cm = 8 cm3
- Banyak kubus kecil = Volume balok / Volume kubus kecil = 576 cm3 / 8 cm3 = 72
- Menuliskan Jawaban: Jadi, banyak kubus kecil yang dapat dihasilkan adalah 72 buah.
Aplikasi Bangun Ruang Sisi Datar dalam Teknologi
Konsep bangun ruang sisi datar tidak hanya terbatas pada pembelajaran matematika, tetapi juga memiliki aplikasi yang luas dalam dunia teknologi. Bangun ruang sisi datar menjadi dasar dalam desain dan pengembangan berbagai teknologi, mulai dari bangunan hingga pesawat terbang.
Desain Bangunan
Bangun ruang sisi datar merupakan fondasi dalam desain bangunan. Arsitek memanfaatkan konsep ini untuk merencanakan struktur bangunan yang kokoh dan efisien.
- Kubus: Bangunan dengan bentuk kubus, seperti rumah bertingkat, memberikan stabilitas struktural dan memaksimalkan ruang.
- Balok: Bangunan dengan bentuk balok, seperti gedung perkantoran, memungkinkan fleksibilitas dalam desain dan penataan ruang.
- Prisma: Bentuk prisma, seperti bangunan dengan atap miring, memberikan ketahanan terhadap angin dan hujan.
- Limas: Bangunan dengan bentuk limas, seperti menara, memberikan kesan monumental dan stabilitas struktural yang tinggi.
Robot
Bangun ruang sisi datar juga berperan penting dalam desain robot. Konsep ini membantu merancang robot yang efisien, mudah bergerak, dan memiliki fungsi spesifik.
- Kubus: Robot dengan bentuk kubus, seperti robot industri, memiliki stabilitas dan kekuatan untuk mengangkat beban berat.
- Balok: Robot dengan bentuk balok, seperti robot pengantar, memiliki ruang yang efisien untuk membawa barang.
- Prisma: Robot dengan bentuk prisma, seperti robot penyelamat, memiliki kemampuan manuver yang baik untuk melewati medan yang sulit.
- Limas: Robot dengan bentuk limas, seperti robot eksplorasi, memiliki stabilitas yang tinggi untuk bergerak di medan yang tidak rata.
Pesawat Terbang
Konsep bangun ruang sisi datar juga diterapkan dalam desain pesawat terbang. Bentuk pesawat terbang yang aerodinamis mengurangi hambatan udara dan meningkatkan efisiensi terbang.
- Kubus: Bentuk kubus tidak efisien untuk pesawat terbang karena menghasilkan hambatan udara yang besar.
- Balok: Bentuk balok juga tidak efisien untuk pesawat terbang karena menghasilkan hambatan udara yang besar.
- Prisma: Bentuk prisma digunakan dalam desain sayap pesawat terbang, memungkinkan aliran udara yang optimal.
- Limas: Bentuk limas digunakan dalam desain hidung pesawat terbang, mengurangi hambatan udara dan meningkatkan stabilitas.
Membuat Model Bangun Ruang Sisi Datar
Membuat model bangun ruang sisi datar dapat membantu dalam memahami konsep-konsep geometri ruang dengan lebih baik. Dengan membuat model sendiri, kita dapat mengamati langsung bentuk, sisi, rusuk, dan titik sudut dari bangun ruang tersebut. Selain itu, kita juga dapat lebih mudah memahami hubungan antara bangun ruang dengan bangun datar yang menjadi sisi-sisinya.
Membuat Model Bangun Ruang Sisi Datar
Berikut langkah-langkah membuat model bangun ruang sisi datar sederhana dari bahan-bahan yang mudah didapat:
- Siapkan bahan-bahan yang diperlukan. Bahan yang dibutuhkan untuk membuat model bangun ruang sisi datar sederhana antara lain:
- Kertas karton
- Gunting
- Lem atau selotip
- Penggaris
- Pensil
- Buat pola bangun datar yang akan menjadi sisi bangun ruang. Misalnya, untuk membuat model kubus, kita perlu membuat 6 pola persegi yang sama besar. Pola ini dapat dibuat dengan menggambar langsung pada kertas karton atau dengan menggunakan pola yang telah dicetak.
- Potong pola bangun datar yang telah dibuat dengan gunting.
- Rekatkan pola bangun datar yang telah dipotong dengan lem atau selotip. Pastikan sisi-sisi yang direkatkan berimpit dengan benar.
- Model bangun ruang sisi datar siap dibuat.
Contoh Model Bangun Ruang Sisi Datar
Sebagai contoh, kita akan membuat model kubus.
- Gambarlah 6 persegi yang sama besar pada kertas karton.
- Potong keenam persegi tersebut dengan gunting.
- Rekatkan keempat persegi tersebut dengan lem atau selotip membentuk sisi-sisi kubus.
- Rekatkan dua persegi sisanya pada sisi kubus yang telah terbentuk, sehingga membentuk tutup dan alas kubus.
Manfaat Membuat Model Bangun Ruang Sisi Datar
Membuat model bangun ruang sisi datar memiliki beberapa manfaat, antara lain:
- Membantu memahami konsep bangun ruang sisi datar dengan lebih baik.
- Meningkatkan kemampuan visualisasi dan pemahaman spasial.
- Membuat pembelajaran geometri ruang lebih menyenangkan dan interaktif.
- Meningkatkan kreativitas dan kemampuan memecahkan masalah.
Ringkasan Penutup
Dengan memahami konsep bangun ruang sisi datar, kita dapat menyelesaikan berbagai masalah geometri yang berkaitan dengan volume, luas permukaan, dan sifat-sifat bangun ruang. Tak hanya itu, pemahaman ini juga dapat diterapkan dalam berbagai bidang kehidupan, mulai dari mendesain rumah hingga membangun infrastruktur. Jadi, mari kita terus asah kemampuan kita dalam memahami dan mengaplikasikan konsep bangun ruang sisi datar!





