Contoh soal vektor matematika – Vektor, dalam matematika, bukan hanya sekadar angka biasa. Vektor memiliki arah dan besar, seperti panah yang menunjukkan arah dan panjangnya. Bayangkan sebuah mobil yang bergerak ke utara dengan kecepatan 60 km/jam. Vektor menggambarkan pergerakan ini, menunjukkan arah (utara) dan besar (60 km/jam). Dalam kehidupan sehari-hari, kita sering menjumpai vektor, seperti arah dan kecepatan angin, gaya yang bekerja pada benda, atau perpindahan suatu objek.
Artikel ini akan membahas berbagai konsep vektor dan penerapannya dalam matematika, disertai contoh soal yang menarik untuk memperjelas pemahaman. Mari kita bahas lebih lanjut tentang operasi vektor, panjang vektor, sudut antara dua vektor, dan banyak lagi.
Pengertian Vektor
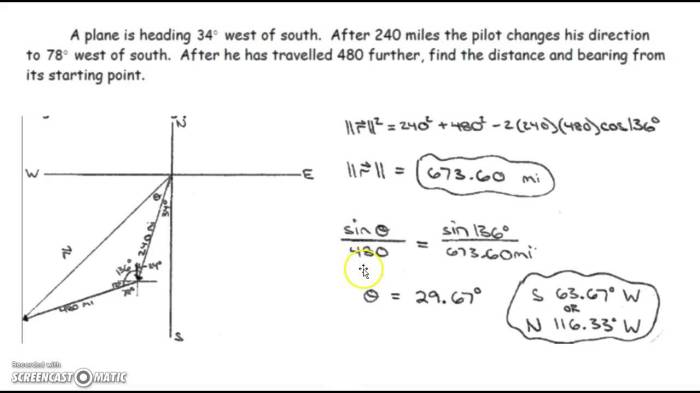
Vektor merupakan suatu besaran yang memiliki nilai dan arah. Dalam matematika, vektor dilambangkan dengan panah yang menunjukkan arah dan panjang panah menunjukkan besarnya nilai vektor. Vektor digunakan untuk merepresentasikan berbagai konsep dalam fisika, teknik, dan ilmu komputer, seperti kecepatan, percepatan, gaya, dan perpindahan.
Contoh Vektor dalam Kehidupan Sehari-hari
Vektor dapat dijumpai di berbagai aspek kehidupan sehari-hari, seperti:
- Perpindahan: Saat seseorang berjalan dari satu titik ke titik lainnya, perpindahannya dapat direpresentasikan sebagai vektor. Arah vektor menunjukkan arah pergerakan, dan panjang vektor menunjukkan jarak yang ditempuh.
- Kecepatan: Kecepatan mobil yang melaju di jalan raya dapat direpresentasikan sebagai vektor. Arah vektor menunjukkan arah mobil bergerak, dan panjang vektor menunjukkan kecepatan mobil.
- Gaya: Ketika seseorang mendorong meja, gaya yang diberikan pada meja dapat direpresentasikan sebagai vektor. Arah vektor menunjukkan arah dorongan, dan panjang vektor menunjukkan besarnya gaya.
Perbedaan Vektor dan Skalar
Vektor dan skalar merupakan konsep yang berbeda dalam matematika. Berikut adalah tabel yang membandingkan keduanya:
| Karakteristik | Vektor | Skalar |
|---|---|---|
| Nilai | Memiliki nilai dan arah | Hanya memiliki nilai |
| Representasi | Panah | Angka |
| Contoh | Kecepatan, percepatan, gaya | Massa, suhu, waktu |
Operasi Vektor
Vektor merupakan besaran yang memiliki nilai dan arah. Dalam matematika, operasi vektor adalah manipulasi vektor untuk menghasilkan vektor baru. Operasi vektor dasar yang akan kita bahas adalah penjumlahan, pengurangan, dan perkalian dengan skalar.
Penjumlahan Vektor
Penjumlahan vektor dilakukan dengan menambahkan komponen-komponen yang bersesuaian dari kedua vektor. Secara geometri, penjumlahan vektor dapat diilustrasikan dengan aturan jajargenjang atau aturan segitiga.
- Aturan Jajargenjang: Dua vektor ditempatkan pada titik awal yang sama, kemudian membentuk jajargenjang dengan vektor tersebut sebagai sisi-sisinya. Vektor hasil penjumlahan adalah diagonal jajargenjang yang berasal dari titik awal.
- Aturan Segitiga: Vektor pertama digambar, kemudian vektor kedua digambar dengan titik awal vektor kedua dihubungkan dengan titik ujung vektor pertama. Vektor hasil penjumlahan adalah vektor yang menghubungkan titik awal vektor pertama dengan titik ujung vektor kedua.
Contoh: Diketahui vektor u = (2, 3) dan v = (1, -1). Penjumlahan vektor u + v adalah:
u + v = (2, 3) + (1, -1) = (2 + 1, 3 – 1) = (3, 2)
Secara geometri, penjumlahan vektor dapat diilustrasikan sebagai berikut: [Gambar ilustrasi penjumlahan vektor dengan aturan jajargenjang dan aturan segitiga].
Pengurangan Vektor
Pengurangan vektor dilakukan dengan mengurangi komponen-komponen yang bersesuaian dari kedua vektor. Secara geometri, pengurangan vektor dapat diilustrasikan dengan menggambar vektor negatif dari vektor yang dikurangi, kemudian melakukan penjumlahan vektor seperti biasa.
Contoh: Diketahui vektor u = (2, 3) dan v = (1, -1). Pengurangan vektor u – v adalah:
u – v = (2, 3) – (1, -1) = (2 – 1, 3 + 1) = (1, 4)
Secara geometri, pengurangan vektor dapat diilustrasikan sebagai berikut: [Gambar ilustrasi pengurangan vektor dengan menggambar vektor negatif dan melakukan penjumlahan].
Perkalian Vektor dengan Skalar
Perkalian vektor dengan skalar adalah operasi yang mengalikan setiap komponen vektor dengan skalar tersebut. Secara geometri, perkalian vektor dengan skalar akan mengubah panjang vektor. Jika skalar positif, panjang vektor akan bertambah. Jika skalar negatif, panjang vektor akan berkurang. Jika skalar sama dengan 1, panjang vektor akan tetap sama.
Contoh: Diketahui vektor u = (2, 3) dan skalar k = 2. Perkalian vektor u dengan skalar k adalah:
ku = 2(2, 3) = (2 * 2, 2 * 3) = (4, 6)
Secara geometri, perkalian vektor dengan skalar dapat diilustrasikan sebagai berikut: [Gambar ilustrasi perkalian vektor dengan skalar, menunjukkan perubahan panjang vektor].
Panjang Vektor
Panjang vektor adalah besaran skalar yang menyatakan jarak dari titik pangkal vektor ke titik ujung vektor. Panjang vektor dapat dihitung dengan menggunakan rumus Pythagoras.
Rumus Menghitung Panjang Vektor
Panjang vektor a = (a1, a2, a3) dapat dihitung dengan rumus berikut:
||a|| = √(a12 + a22 + a32)
Contoh Soal Menghitung Panjang Vektor, Contoh soal vektor matematika
Misalkan terdapat vektor a = (3, 4, 0). Panjang vektor a dapat dihitung sebagai berikut:
||a|| = √(32 + 42 + 02) = √(9 + 16 + 0) = √25 = 5
Jadi, panjang vektor a adalah 5.
Hubungan Panjang Vektor dengan Jarak Dua Titik
Panjang vektor dapat diinterpretasikan sebagai jarak antara titik pangkal dan titik ujung vektor. Misalkan titik A dan titik B memiliki koordinat (x1, y1, z1) dan (x2, y2, z2) masing-masing. Vektor AB yang menghubungkan titik A dan titik B dapat ditulis sebagai:
AB = (x2 – x1, y2 – y1, z2 – z1)
Panjang vektor AB sama dengan jarak antara titik A dan titik B, yang dapat dihitung dengan rumus:
||AB|| = √((x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2)
Berikut adalah tabel yang menunjukkan hubungan antara panjang vektor dengan jarak dua titik:
| Panjang Vektor | Jarak Dua Titik |
|---|---|
| ||a|| | Jarak antara titik pangkal dan titik ujung vektor a |
| ||AB|| | Jarak antara titik A dan titik B |
Vektor Satuan
Dalam dunia vektor, vektor satuan adalah konsep penting yang digunakan untuk mewakili arah suatu vektor. Vektor satuan memiliki panjang 1 dan digunakan untuk menunjukkan arah suatu vektor tanpa mempertimbangkan besarnya. Pemahaman tentang vektor satuan sangat penting dalam berbagai bidang matematika, seperti geometri, fisika, dan ilmu komputer.
Pengertian Vektor Satuan
Vektor satuan adalah vektor yang memiliki panjang 1. Vektor satuan sering dilambangkan dengan topi (^) di atas simbol vektor. Misalnya, vektor satuan dari vektor v ditulis sebagai v̂.
Mencari Vektor Satuan
Untuk mencari vektor satuan dari suatu vektor, kita dapat menggunakan rumus berikut:
v̂ = v / |v|
Dimana:
- v̂ adalah vektor satuan dari vektor v
- v adalah vektor yang ingin dicari vektor satuannya
- |v| adalah besarnya vektor v
Contoh:
Misalkan kita memiliki vektor v = (3, 4). Untuk mencari vektor satuan dari v, kita perlu menghitung besarnya vektor v terlebih dahulu.
Contoh soal vektor matematika bisa membantu kamu memahami konsep dasar seperti penjumlahan, pengurangan, dan perkalian vektor. Begitu juga dengan contoh soal ekonomi manajerial, yang bisa kamu temukan di situs ini , yang akan membantumu memahami konsep-konsep penting seperti biaya, keuntungan, dan permintaan.
Sama seperti contoh soal vektor matematika, contoh soal ekonomi manajerial juga akan menguji kemampuanmu dalam memecahkan masalah dan menerapkan teori yang kamu pelajari.
|v| = √(3² + 4²) = √(9 + 16) = √25 = 5
Kemudian, kita dapat mencari vektor satuannya:
v̂ = v / |v| = (3, 4) / 5 = (3/5, 4/5)
Jadi, vektor satuan dari vektor v = (3, 4) adalah v̂ = (3/5, 4/5).
Kegunaan Vektor Satuan
Vektor satuan memiliki berbagai kegunaan dalam matematika, antara lain:
- Menyatakan arah suatu vektor: Vektor satuan digunakan untuk menunjukkan arah suatu vektor tanpa mempertimbangkan besarnya. Ini berguna dalam berbagai aplikasi, seperti dalam fisika untuk menggambarkan arah gaya atau kecepatan.
- Memproyeksikan vektor ke sumbu: Vektor satuan dapat digunakan untuk memproyeksikan vektor ke sumbu tertentu. Ini berguna dalam geometri analitik untuk menentukan koordinat titik dalam ruang.
- Membuat basis vektor: Vektor satuan dapat digunakan untuk membuat basis vektor, yang merupakan himpunan vektor linear independen yang dapat digunakan untuk menyatakan semua vektor dalam ruang vektor tertentu. Ini sangat penting dalam aljabar linear.
- Membuat persamaan garis: Vektor satuan dapat digunakan untuk membuat persamaan garis yang melewati titik tertentu dan memiliki arah tertentu. Ini berguna dalam geometri analitik untuk menentukan persamaan garis.
Sudut Antara Dua Vektor
Sudut antara dua vektor adalah besaran yang menunjukkan seberapa besar perbedaan arah antara kedua vektor tersebut. Sudut ini sangat penting dalam berbagai aplikasi matematika, fisika, dan teknik, terutama dalam memahami hubungan antara dua vektor.
Rumus Menghitung Sudut Antara Dua Vektor
Rumus untuk menghitung sudut antara dua vektor, u dan v, adalah:
cos θ = (u ⋅ v) / (||u|| ||v||)
Dimana:
- θ adalah sudut antara vektor u dan v.
- u ⋅ v adalah hasil kali dot (dot product) antara vektor u dan v.
- ||u|| adalah panjang (magnitude) vektor u.
- ||v|| adalah panjang (magnitude) vektor v.
Rumus ini didasarkan pada konsep hasil kali dot, yang menghubungkan sudut antara dua vektor dengan panjangnya.
Contoh Soal Menghitung Sudut Antara Dua Vektor
Misalkan kita memiliki dua vektor, u = (2, 3) dan v = (4, 1). Untuk menghitung sudut antara kedua vektor ini, kita dapat menggunakan rumus di atas:
- Hitung hasil kali dot (dot product) antara u dan v:
u ⋅ v = (2)(4) + (3)(1) = 11 - Hitung panjang (magnitude) vektor u:
||u|| = √(2² + 3²) = √13 - Hitung panjang (magnitude) vektor v:
||v|| = √(4² + 1²) = √17 - Substitusikan nilai-nilai yang diperoleh ke dalam rumus:
cos θ = 11 / (√13 √17) ≈ 0.79 - Hitung sudut θ dengan menggunakan fungsi arccosine (cos⁻¹):
θ ≈ cos⁻¹(0.79) ≈ 37.9°
Jadi, sudut antara vektor u = (2, 3) dan v = (4, 1) adalah sekitar 37.9°.
Hubungan Sudut Antara Dua Vektor dengan Proyeksi Vektor
Sudut antara dua vektor erat kaitannya dengan konsep proyeksi vektor. Proyeksi vektor u pada vektor v adalah vektor yang merupakan bayangan u pada arah v. Panjang proyeksi ini dihitung dengan rumus:
||projvu|| = ||u|| cos θ
Dimana θ adalah sudut antara u dan v. Rumus ini menunjukkan bahwa panjang proyeksi u pada v bergantung pada panjang u dan cosinus sudut antara kedua vektor.
Semakin kecil sudut antara u dan v, semakin besar panjang proyeksi u pada v. Sebaliknya, semakin besar sudut antara u dan v, semakin kecil panjang proyeksi u pada v.
Proyeksi Vektor
Proyeksi vektor merupakan konsep penting dalam aljabar linear yang memungkinkan kita untuk menguraikan suatu vektor ke dalam komponen yang sejajar dan tegak lurus terhadap vektor lainnya. Dalam konteks geometri, proyeksi vektor dapat dibayangkan sebagai “bayangan” dari suatu vektor pada vektor lainnya.
Pengertian Proyeksi Vektor
Proyeksi vektor u pada vektor v adalah vektor yang sejajar dengan v dan memiliki panjang yang sama dengan panjang proyeksi ortogonal u pada v. Secara matematis, proyeksi vektor u pada v dinotasikan sebagai projv u.
Contoh Soal Mencari Proyeksi Vektor
Misalkan kita memiliki vektor u = (3, 4) dan v = (1, 2). Untuk mencari proyeksi vektor u pada v, kita dapat menggunakan rumus berikut:
projv u = ((u · v) / ||v||2) v
Dimana:
- u · v adalah hasil perkalian dot antara vektor u dan v.
- ||v||2 adalah kuadrat dari panjang vektor v.
Langkah-langkahnya adalah:
- Hitung perkalian dot antara u dan v: u · v = (3)(1) + (4)(2) = 11
- Hitung kuadrat panjang vektor v: ||v||2 = (1)2 + (2)2 = 5
- Substitusikan nilai yang diperoleh ke dalam rumus: projv u = (11/5) (1, 2) = (11/5, 22/5)
Jadi, proyeksi vektor u pada v adalah (11/5, 22/5).
Kegunaan Proyeksi Vektor dalam Matematika
Proyeksi vektor memiliki berbagai kegunaan dalam matematika, antara lain:
- Menentukan jarak terdekat antara titik dan garis: Proyeksi vektor dapat digunakan untuk mencari titik pada garis yang paling dekat dengan titik tertentu di luar garis.
- Mencari komponen vektor yang sejajar dan tegak lurus terhadap vektor lainnya: Proyeksi vektor memungkinkan kita untuk menguraikan vektor menjadi dua komponen yang saling tegak lurus.
- Memecahkan masalah geometri dan fisika: Proyeksi vektor digunakan dalam berbagai aplikasi, seperti menghitung gaya yang bekerja pada benda, menghitung kecepatan relatif, dan menentukan posisi benda dalam ruang.
Vektor Ortogonal
Dalam dunia vektor, konsep ortogonalitas memainkan peran penting dalam memahami hubungan antar vektor. Dua vektor dikatakan ortogonal jika membentuk sudut 90 derajat satu sama lain. Konsep ini memiliki aplikasi luas dalam berbagai bidang, seperti geometri, fisika, dan ilmu komputer.
Pengertian Vektor Ortogonal
Vektor ortogonal adalah dua vektor yang saling tegak lurus. Dengan kata lain, sudut antara kedua vektor tersebut adalah 90 derajat. Hal ini dapat divisualisasikan sebagai dua garis yang saling berpotongan pada titik sudut siku-siku.
Menentukan Apakah Dua Vektor Ortogonal
Untuk menentukan apakah dua vektor ortogonal, kita dapat menggunakan konsep perkalian dot. Perkalian dot dari dua vektor menghasilkan skalar yang merupakan hasil kali dari panjang kedua vektor dan kosinus sudut antara keduanya.
Jika perkalian dot dari dua vektor sama dengan nol, maka kedua vektor tersebut ortogonal.
- Misalkan vektor a = (a1, a2, a3) dan vektor b = (b1, b2, b3).
- Perkalian dot dari a dan b didefinisikan sebagai: a · b = a1b1 + a2b2 + a3b3.
- Jika a · b = 0, maka vektor a dan b ortogonal.
Hubungan Vektor Ortogonal dengan Perkalian Dot
Perkalian dot merupakan alat yang ampuh untuk menentukan ortogonalitas antara dua vektor. Hal ini dikarenakan hubungan langsung antara perkalian dot dan sudut antara kedua vektor.
a · b = ||a|| ||b|| cos θ
Dimana θ adalah sudut antara vektor a dan b. Jika θ = 90 derajat, maka cos θ = 0, sehingga a · b = 0. Ini menunjukkan bahwa jika perkalian dot dari dua vektor sama dengan nol, maka kedua vektor tersebut ortogonal.
Perkalian Dot
Perkalian dot adalah operasi yang menggabungkan dua vektor dan menghasilkan skalar, yaitu sebuah angka. Operasi ini memiliki banyak aplikasi dalam berbagai bidang matematika dan fisika. Perkalian dot memberikan informasi tentang hubungan sudut antara dua vektor.
Rumus Perkalian Dot
Rumus perkalian dot antara dua vektor a = (a1, a2, …, an) dan b = (b1, b2, …, bn) adalah:
a · b = a1b1 + a2b2 + … + anbn
Perhatikan bahwa perkalian dot adalah operasi komutatif, artinya a · b = b · a.
Contoh Soal Perkalian Dot
Misalkan kita memiliki dua vektor a = (2, 3, 1) dan b = (1, -1, 2). Perkalian dot antara a dan b adalah:
a · b = (2)(1) + (3)(-1) + (1)(2) = 1
Kegunaan Perkalian Dot dalam Matematika
Perkalian dot memiliki beberapa kegunaan penting dalam matematika, di antaranya:
- Menentukan sudut antara dua vektor: Perkalian dot dapat digunakan untuk menghitung kosinus sudut antara dua vektor. Rumusnya adalah:
- Menentukan proyeksi vektor: Perkalian dot dapat digunakan untuk menghitung proyeksi vektor a pada vektor b. Rumusnya adalah:
- Menentukan apakah dua vektor ortogonal: Dua vektor dikatakan ortogonal jika perkalian dot mereka sama dengan nol.
cos θ = (a · b) / (||a|| ||b||)
projb a = ((a · b) / (||b||2)) b
Perkalian Cross
Perkalian cross, atau perkalian vektor, adalah operasi matematika yang menghasilkan vektor baru yang tegak lurus terhadap kedua vektor yang dikalikan. Operasi ini memiliki aplikasi penting dalam berbagai bidang seperti fisika, geometri, dan pemrograman komputer.
Rumus Perkalian Cross
Perkalian cross antara dua vektor, a dan b, didefinisikan sebagai berikut:
a x b = ||a|| ||b|| sin θ n
Dimana:
- ||a|| dan ||b|| adalah besarnya vektor a dan b, masing-masing.
- θ adalah sudut antara vektor a dan b.
- n adalah vektor satuan yang tegak lurus terhadap bidang yang dibentuk oleh a dan b, arahnya ditentukan oleh aturan tangan kanan.
Contoh Soal Perkalian Cross
Misalkan kita memiliki dua vektor:
- a = (1, 2, 3)
- b = (4, 5, 6)
Untuk menghitung perkalian cross antara a dan b, kita dapat menggunakan rumus determinan:
a x b =
| i j k |
| 1 2 3 |
| 4 5 6 |
Dengan menghitung determinan, kita memperoleh:
a x b = (-3, 6, -3)
Kegunaan Perkalian Cross
Perkalian cross memiliki banyak kegunaan dalam matematika dan bidang terkait, di antaranya:
- Menentukan vektor normal terhadap bidang: Perkalian cross dua vektor pada bidang menghasilkan vektor normal terhadap bidang tersebut.
- Menghitung momen torsi: Dalam fisika, momen torsi yang dihasilkan oleh gaya pada suatu titik dapat dihitung dengan menggunakan perkalian cross antara vektor gaya dan vektor posisi titik tersebut.
- Menghitung luas paralelogram: Luas paralelogram yang dibentuk oleh dua vektor sama dengan besarnya perkalian cross kedua vektor tersebut.
- Menghitung volume paralelepiped: Volume paralelepiped yang dibentuk oleh tiga vektor sama dengan besarnya perkalian titik vektor ketiga dengan perkalian cross dua vektor pertama.
Penerapan Vektor dalam Geometri
Vektor merupakan alat yang sangat berguna dalam geometri, terutama dalam geometri analitik. Vektor memungkinkan kita untuk merepresentasikan titik, garis, dan bidang dengan cara yang mudah dan efisien. Dengan menggunakan vektor, kita dapat melakukan berbagai operasi geometri seperti mencari jarak, sudut, dan persamaan garis dan bidang.
Menentukan Persamaan Garis Menggunakan Vektor
Persamaan garis dapat ditentukan dengan menggunakan vektor. Kita dapat menggunakan dua vektor untuk menentukan garis, yaitu vektor arah dan vektor posisi. Vektor arah menunjukkan arah garis, sedangkan vektor posisi menunjukkan titik yang dilalui garis.
- Vektor arah garis adalah vektor yang sejajar dengan garis tersebut.
- Vektor posisi adalah vektor yang menghubungkan titik asal ke titik yang dilalui garis.
Persamaan garis dapat ditulis dalam bentuk vektor sebagai berikut:
r = a + tb
Dimana:
- r adalah vektor posisi titik yang berada di garis.
- a adalah vektor posisi titik yang dilalui garis.
- b adalah vektor arah garis.
- t adalah parameter skalar.
Persamaan garis juga dapat ditulis dalam bentuk parametrik dengan memisahkan komponen-komponen vektor r, a, dan b:
x = ax + tbx
y = ay + tby
z = az + tbz
Dimana:
- x, y, dan z adalah koordinat titik yang berada di garis.
- ax, ay, dan az adalah koordinat titik yang dilalui garis.
- bx, by, dan bz adalah komponen vektor arah garis.
Contoh Soal Menentukan Persamaan Garis Menggunakan Vektor
Misalkan kita ingin menentukan persamaan garis yang melalui titik A(1, 2, 3) dan sejajar dengan vektor b = (2, 1, -1). Vektor posisi titik A adalah a = (1, 2, 3). Dengan menggunakan persamaan vektor garis, kita dapat menentukan persamaan garis sebagai berikut:
r = (1, 2, 3) + t(2, 1, -1)
Atau dalam bentuk parametrik:
x = 1 + 2t
y = 2 + t
z = 3 – t
Menentukan Persamaan Bidang Menggunakan Vektor
Persamaan bidang dapat ditentukan dengan menggunakan vektor normal dan vektor posisi. Vektor normal adalah vektor yang tegak lurus terhadap bidang, sedangkan vektor posisi menunjukkan titik yang dilalui bidang.
- Vektor normal bidang adalah vektor yang tegak lurus terhadap bidang tersebut.
- Vektor posisi adalah vektor yang menghubungkan titik asal ke titik yang dilalui bidang.
Persamaan bidang dapat ditulis dalam bentuk vektor sebagai berikut:
n · (r – a) = 0
Dimana:
- n adalah vektor normal bidang.
- r adalah vektor posisi titik yang berada di bidang.
- a adalah vektor posisi titik yang dilalui bidang.
Persamaan bidang juga dapat ditulis dalam bentuk skalar dengan memisahkan komponen-komponen vektor n, r, dan a:
nx(x – ax) + ny(y – ay) + nz(z – az) = 0
Dimana:
- nx, ny, dan nz adalah komponen vektor normal bidang.
- x, y, dan z adalah koordinat titik yang berada di bidang.
- ax, ay, dan az adalah koordinat titik yang dilalui bidang.
Contoh Soal Menentukan Persamaan Bidang Menggunakan Vektor
Misalkan kita ingin menentukan persamaan bidang yang melalui titik A(1, 2, 3) dan tegak lurus dengan vektor n = (2, 1, -1). Vektor posisi titik A adalah a = (1, 2, 3). Dengan menggunakan persamaan vektor bidang, kita dapat menentukan persamaan bidang sebagai berikut:
(2, 1, -1) · (r – (1, 2, 3)) = 0
Atau dalam bentuk skalar:
2(x – 1) + (y – 2) – (z – 3) = 0
Kegunaan Vektor dalam Geometri Analitik
Vektor memiliki banyak kegunaan dalam geometri analitik, di antaranya:
- Menentukan jarak antara dua titik.
- Menentukan sudut antara dua vektor.
- Menentukan persamaan garis dan bidang.
- Menentukan persamaan lingkaran dan elips.
- Menentukan volume dan luas permukaan bangun ruang.
Dengan menggunakan vektor, kita dapat menyelesaikan berbagai masalah geometri dengan lebih mudah dan efisien. Vektor juga membantu kita dalam memahami konsep geometri secara lebih mendalam.
Ringkasan Akhir: Contoh Soal Vektor Matematika
Vektor merupakan konsep penting dalam matematika yang memiliki aplikasi luas dalam berbagai bidang, seperti fisika, teknik, dan ilmu komputer. Dengan memahami konsep vektor, kita dapat menyelesaikan masalah-masalah yang melibatkan arah dan besar, serta mengaplikasikannya dalam berbagai bidang ilmu pengetahuan dan teknologi.





