Contoh soal invers matriks ordo 2×2 dan jawabannya – Pernahkah Anda merasa kesulitan dalam memahami konsep invers matriks? Terutama dalam matriks ordo 2×2? Tenang, artikel ini akan membantu Anda memahami konsep tersebut dengan mudah melalui contoh soal dan jawaban yang lengkap. Invers matriks adalah konsep penting dalam aljabar linear, dan memahaminya dapat membantu Anda menyelesaikan berbagai permasalahan matematika, terutama dalam sistem persamaan linear.
Artikel ini akan membahas secara rinci tentang cara menentukan invers matriks ordo 2×2, lengkap dengan rumus dan langkah-langkahnya. Selain itu, Anda juga akan menemukan contoh soal dan jawaban yang beragam, mulai dari matriks dengan determinan nol hingga matriks dengan determinan tidak nol. Siap untuk mempelajari tentang invers matriks? Mari kita mulai!
Pengertian Invers Matriks Ordo 2×2
Invers matriks adalah konsep penting dalam aljabar linear. Invers matriks merupakan matriks yang ketika dikalikan dengan matriks aslinya menghasilkan matriks identitas. Matriks identitas adalah matriks persegi dengan elemen diagonal utama bernilai 1 dan elemen lainnya bernilai 0. Invers matriks dilambangkan dengan simbol “-1” di atas matriks.
Invers matriks ordo 2×2, yaitu matriks yang memiliki dua baris dan dua kolom, memiliki definisi dan cara penentuan yang spesifik. Matriks ordo 2×2 yang memiliki invers disebut matriks nonsingular.
Contoh Matriks Ordo 2×2 dan Inversnya
Misalnya, kita memiliki matriks A dengan:
A =
2 1 3 4
Invers dari matriks A, yaitu A-1, dapat dihitung dengan rumus berikut:
A-1 = 1/(ad-bc)
d -b -c a
dengan a, b, c, dan d adalah elemen-elemen matriks A:
A =
a b c d
Dalam contoh matriks A, a=2, b=1, c=3, dan d=4. Maka invers dari matriks A adalah:
A-1 = 1/((2*4)-(1*3))
4 -1 -3 2
A-1 = 1/5
4 -1 -3 2
A-1 =
4/5 -1/5 -3/5 2/5
Syarat Matriks Ordo 2×2 Memiliki Invers
Tidak semua matriks ordo 2×2 memiliki invers. Syarat sebuah matriks ordo 2×2 memiliki invers adalah determinan matriks tersebut tidak sama dengan nol. Determinan matriks adalah nilai skalar yang terkait dengan matriks persegi. Determinan matriks A yang memiliki elemen a, b, c, dan d dihitung dengan rumus:
det(A) = ad – bc
Jika determinan matriks A sama dengan nol, maka matriks A tidak memiliki invers. Dalam hal ini, matriks A disebut sebagai matriks singular.
Rumus Menentukan Invers Matriks Ordo 2×2
Dalam aljabar linear, invers matriks merupakan konsep penting yang memungkinkan kita untuk menyelesaikan sistem persamaan linear dan melakukan berbagai operasi matriks lainnya. Invers matriks ordo 2×2, khususnya, memiliki aplikasi yang luas dalam berbagai bidang, seperti ilmu komputer, fisika, dan ekonomi.
Rumus Umum Invers Matriks Ordo 2×2
Untuk menentukan invers matriks ordo 2×2, kita dapat menggunakan rumus umum berikut:
Jika A =
[ a b ]
[ c d ]
, maka invers A, dinotasikan sebagai A-1, adalah:A-1 =
[ d -b ]
[ -c a ]
/ (ad – bc)dengan (ad – bc) ≠ 0
Rumus ini menunjukkan bahwa invers matriks A dapat diperoleh dengan menukar elemen diagonal utama (a dan d), mengubah tanda elemen diagonal sekunder (b dan c), dan membagi seluruh matriks dengan determinan matriks A, yaitu (ad – bc).
Langkah-langkah Menentukan Invers Matriks Ordo 2×2
Berikut langkah-langkah yang dapat digunakan untuk menentukan invers matriks ordo 2×2:
- Tentukan determinan matriks A, yaitu (ad – bc).
- Jika determinan matriks A tidak sama dengan nol (ad – bc ≠ 0), maka matriks A memiliki invers. Jika determinan matriks A sama dengan nol (ad – bc = 0), maka matriks A tidak memiliki invers.
- Tukar elemen diagonal utama (a dan d) dan ubah tanda elemen diagonal sekunder (b dan c).
- Bagi setiap elemen matriks yang dihasilkan dengan determinan matriks A, (ad – bc).
- Hasilnya adalah invers matriks A, A-1.
Contoh Perhitungan Invers Matriks Ordo 2×2
Misalkan kita memiliki matriks A:
A =
[ 2 1 ]
[ 4 3 ]
Untuk menentukan invers matriks A, kita dapat mengikuti langkah-langkah di atas:
- Tentukan determinan matriks A: (2 * 3) – (1 * 4) = 2.
- Determinan matriks A tidak sama dengan nol, maka matriks A memiliki invers.
- Tukar elemen diagonal utama dan ubah tanda elemen diagonal sekunder:
[ 3 -1 ]
[ -4 2 ] - Bagi setiap elemen matriks yang dihasilkan dengan determinan matriks A, 2:
[ 3/2 -1/2 ]
[ -2 1 ] - Hasilnya adalah invers matriks A:
A-1 =
[ 3/2 -1/2 ]
[ -2 1 ]
Dengan demikian, invers matriks A adalah:
A-1 =
[ 3/2 -1/2 ]
[ -2 1 ]
Nggak cuma soal invers matriks ordo 2×2 dan jawabannya yang bikin kepala pusing, soal willdan be going tojuga bisa jadi tantangan tersendiri, ya. Tapi tenang, kamu bisa kok belajar bareng-bareng di contoh soal will dan be going to ini. Nah, kalau udah paham soal willdan be going to, balik lagi deh ke soal invers matriks ordo 2×2.
Yakin deh, pasti bisa dipecahkan dengan mudah!
Contoh Soal Invers Matriks Ordo 2×2 dan Jawabannya
Pada materi aljabar linear, invers matriks merupakan konsep penting yang berkaitan dengan operasi kebalikan dari perkalian matriks. Dalam invers matriks, kita mencari matriks lain yang jika dikalikan dengan matriks asalnya akan menghasilkan matriks identitas. Untuk matriks ordo 2×2, proses mencari inversnya melibatkan beberapa langkah sederhana yang melibatkan determinan dan beberapa operasi dasar.
Pada artikel ini, kita akan membahas beberapa contoh soal invers matriks ordo 2×2 beserta jawabannya. Contoh-contoh ini akan membantu Anda memahami cara mencari invers matriks ordo 2×2 dan bagaimana mengaplikasikan konsep tersebut dalam berbagai situasi.
Contoh Soal Invers Matriks Ordo 2×2 dan Jawabannya
Berikut adalah tabel yang berisi 5 contoh soal invers matriks ordo 2×2 dan jawabannya. Tabel ini mencakup berbagai jenis matriks, termasuk matriks dengan determinan 0.
| No | Matriks | Determinan | Invers Matriks |
|---|---|---|---|
| 1 | 2143 | (2×3)-(1×4)=2 | 123-1-42=32-12-21 |
| 2 | 1234 | (1×4)-(2×3)=-2 | -124-2-31=-2132-12 |
| 3 | 53106 | (5×6)-(3×10)=0 | Tidak memiliki invers |
| 4 | 7231 | (7×1)-(2×3)=1 | 111-2-37=1-2-37 |
| 5 | 0123 | (0×3)-(1×2)=-2 | -123-1-20=-321210 |
Penerapan Invers Matriks Ordo 2×2: Contoh Soal Invers Matriks Ordo 2×2 Dan Jawabannya
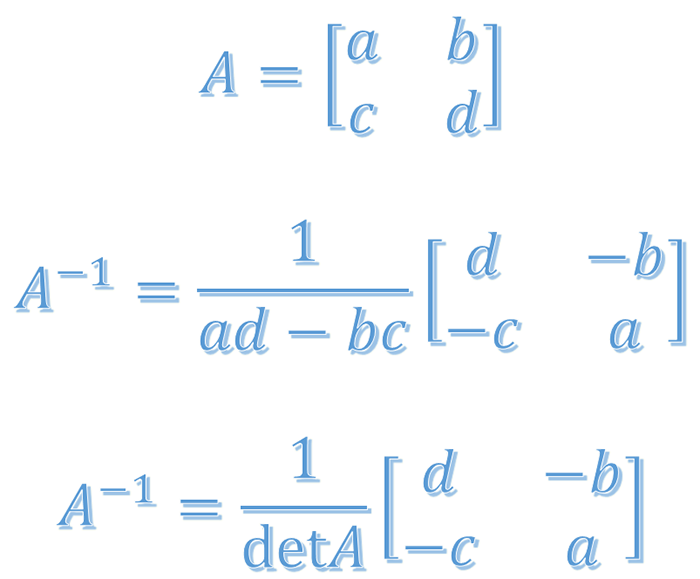
Invers matriks ordo 2×2 memiliki aplikasi penting dalam berbagai bidang, terutama dalam menyelesaikan sistem persamaan linear dua variabel. Dengan memanfaatkan invers matriks, kita dapat menemukan solusi unik untuk sistem persamaan tersebut dengan cara yang sistematis dan efisien.
Sistem Persamaan Linear Dua Variabel dengan Invers Matriks
Invers matriks digunakan untuk menyelesaikan sistem persamaan linear dua variabel dengan mengubah sistem tersebut ke dalam bentuk matriks. Langkah-langkahnya adalah sebagai berikut:
- Tulis sistem persamaan linear dua variabel dalam bentuk matriks, yaitu AX = B, di mana A adalah matriks koefisien, X adalah matriks variabel, dan B adalah matriks konstanta.
- Hitung invers matriks A, yaitu A-1.
- Kalikan kedua sisi persamaan matriks AX = B dengan A-1, sehingga diperoleh X = A-1B.
- Hitung hasil perkalian A-1B untuk mendapatkan nilai variabel X.
Contoh Soal Sistem Persamaan Linear Dua Variabel
Sebagai contoh, perhatikan sistem persamaan linear dua variabel berikut:
2x + 3y = 7
x – 2y = -1
Untuk menyelesaikan sistem persamaan ini dengan invers matriks, ikuti langkah-langkah berikut:
- Tulis sistem persamaan dalam bentuk matriks:
2 3 1 -2 x y =
7 -1 - Hitung invers matriks A:
A-1 = 1/(-4 – 3)
-2 -3 -1 2 =
2/7 3/7 1/7 -2/7 - Kalikan kedua sisi persamaan matriks dengan A-1:
2/7 3/7 1/7 -2/7 2 3 1 -2 x y =
2/7 3/7 1/7 -2/7 7 -1 - Hitung hasil perkalian A-1B:
x y =
2/7 * 7 + 3/7 * -1 1/7 * 7 – 2/7 * -1 =
11/7 9/7
Jadi, solusi sistem persamaan linear dua variabel tersebut adalah x = 11/7 dan y = 9/7.
Sifat-Sifat Invers Matriks Ordo 2×2
Selain memahami cara mencari invers matriks ordo 2×2, penting juga untuk memahami sifat-sifat yang dimiliki oleh invers matriks. Sifat-sifat ini membantu kita dalam memahami lebih dalam tentang operasi matriks dan bagaimana invers matriks berperan dalam berbagai aplikasi matematika.
Sifat Komutatif
Sifat komutatif dalam operasi invers matriks menyatakan bahwa urutan perkalian matriks dengan inversnya tidak berpengaruh pada hasil akhir. Dengan kata lain, hasil perkalian matriks A dengan inversnya (A-1) akan sama dengan hasil perkalian inversnya (A-1) dengan matriks A.
A * A-1 = A-1 * A = I
Dimana I adalah matriks identitas. Misalnya, jika kita memiliki matriks A = [[2, 1], [3, 2]] dan inversnya A-1 = [[2, -1], [-3, 2]], maka:
A * A-1 = [[2, 1], [3, 2]] * [[2, -1], [-3, 2]] = [[1, 0], [0, 1]]
A-1 * A = [[2, -1], [-3, 2]] * [[2, 1], [3, 2]] = [[1, 0], [0, 1]]
Hasil perkaliannya sama dengan matriks identitas I = [[1, 0], [0, 1]].
Sifat Asosiatif
Sifat asosiatif dalam operasi invers matriks menyatakan bahwa urutan perkalian tiga matriks atau lebih tidak berpengaruh pada hasil akhir, selama urutan matriks dan inversnya tetap sama.
(A * B) * C-1 = A * (B * C-1)
Misalnya, jika kita memiliki matriks A = [[1, 2], [3, 4]], B = [[2, 1], [1, 2]], dan C = [[3, 1], [2, 1]], maka:
(A * B) * C-1 = ([[1, 2], [3, 4]] * [[2, 1], [1, 2]]) * [[1, -1], [-2, 3]] = [[4, 5], [10, 11]] * [[1, -1], [-2, 3]] = [[6, -1], [14, -1]]
A * (B * C-1) = [[1, 2], [3, 4]] * ([[2, 1], [1, 2]] * [[1, -1], [-2, 3]]) = [[1, 2], [3, 4]] * [[0, 1], [-3, 5]] = [[6, -1], [14, -1]]
Hasil perkaliannya sama.
Sifat Identitas
Sifat identitas dalam operasi invers matriks menyatakan bahwa perkalian matriks dengan matriks identitas akan menghasilkan matriks itu sendiri.
A * I = A
Dimana I adalah matriks identitas. Misalnya, jika kita memiliki matriks A = [[2, 1], [3, 2]] dan matriks identitas I = [[1, 0], [0, 1]], maka:
A * I = [[2, 1], [3, 2]] * [[1, 0], [0, 1]] = [[2, 1], [3, 2]]
Hasil perkaliannya sama dengan matriks A.
Kesalahan Umum dalam Menentukan Invers Matriks Ordo 2×2
Menentukan invers matriks ordo 2×2 merupakan langkah penting dalam menyelesaikan persamaan linear dan berbagai masalah matematika lainnya. Meskipun rumusnya relatif sederhana, beberapa kesalahan umum seringkali terjadi. Memahami kesalahan-kesalahan ini dan cara menghindarinya dapat meningkatkan keakuratan dan efisiensi dalam menyelesaikan masalah matriks.
Kesalahan dalam Menghitung Determinan
Determinan matriks merupakan langkah awal yang krusial dalam menentukan invers. Kesalahan dalam menghitung determinan akan berakibat fatal pada hasil akhir.
- Kesalahan Umum: Salah dalam mengidentifikasi elemen diagonal utama dan diagonal sekunder, atau salah dalam menghitung perkalian elemen-elemen tersebut.
- Cara Menghindari: Pastikan memahami definisi determinan matriks ordo 2×2, yaitu selisih antara perkalian elemen diagonal utama dengan perkalian elemen diagonal sekunder.
- Contoh:
Misalkan kita ingin menentukan determinan matriks A =
\[
\beginpmatrix
2 & 3 \\
1 & 4
\endpmatrix
\]Kesalahan umum adalah dengan menjumlahkan perkalian elemen diagonal utama dan diagonal sekunder. Yang benar adalah:
\[
det(A) = (2 \times 4) – (3 \times 1) = 8 – 3 = 5
\]
Kesalahan dalam Menukar Elemen Diagonal
Setelah determinan diperoleh, langkah selanjutnya adalah menukar elemen diagonal utama.
- Kesalahan Umum: Lupa menukar elemen diagonal utama, atau salah dalam menukar posisi elemen.
- Cara Menghindari: Pastikan elemen diagonal utama saling bertukar posisi. Ingat bahwa elemen diagonal utama adalah elemen yang terletak pada garis diagonal dari kiri atas ke kanan bawah.
- Contoh:
Misalkan matriks A =
\[
\beginpmatrix
2 & 3 \\
1 & 4
\endpmatrix
\]Setelah determinan dihitung, langkah selanjutnya adalah menukar elemen diagonal utama. Kesalahan umum adalah dengan menukar elemen baris pertama kolom kedua dengan elemen baris kedua kolom pertama, yang seharusnya menjadi elemen baris pertama kolom pertama dan elemen baris kedua kolom kedua yang saling bertukar. Hasilnya seharusnya:
\[
\beginpmatrix
4 & 3 \\
1 & 2
\endpmatrix
\]
Kesalahan dalam Mengubah Tanda Elemen Non-Diagonal
Langkah selanjutnya adalah mengubah tanda elemen non-diagonal.
- Kesalahan Umum: Lupa mengubah tanda elemen non-diagonal, atau salah dalam mengubah tanda.
- Cara Menghindari: Pastikan semua elemen non-diagonal, yaitu elemen yang tidak terletak pada diagonal utama, diubah tandanya. Ingat bahwa elemen non-diagonal adalah elemen yang terletak pada garis diagonal dari kiri bawah ke kanan atas.
- Contoh:
Misalkan matriks A =
\[
\beginpmatrix
2 & 3 \\
1 & 4
\endpmatrix
\]Setelah menukar elemen diagonal utama, langkah selanjutnya adalah mengubah tanda elemen non-diagonal. Kesalahan umum adalah dengan hanya mengubah tanda satu elemen non-diagonal, yang seharusnya kedua elemen non-diagonal diubah tandanya. Hasilnya seharusnya:
\[
\beginpmatrix
4 & -3 \\
-1 & 2
\endpmatrix
\]
Kesalahan dalam Membagi dengan Determinan, Contoh soal invers matriks ordo 2×2 dan jawabannya
Langkah terakhir adalah membagi matriks yang telah dimodifikasi dengan determinan.
- Kesalahan Umum: Lupa membagi dengan determinan, atau salah dalam membagi setiap elemen matriks dengan determinan.
- Cara Menghindari: Pastikan setiap elemen matriks dibagi dengan determinan. Ingat bahwa determinan adalah nilai yang telah dihitung sebelumnya.
- Contoh:
Misalkan matriks A =
\[
\beginpmatrix
2 & 3 \\
1 & 4
\endpmatrix
\]Setelah mengubah tanda elemen non-diagonal, langkah selanjutnya adalah membagi matriks dengan determinan. Kesalahan umum adalah dengan hanya membagi satu elemen matriks dengan determinan, yang seharusnya semua elemen matriks dibagi dengan determinan. Hasilnya seharusnya:
\[
A^-1 = \frac15
\beginpmatrix
4 & -3 \\
-1 & 2
\endpmatrix
\]
Ringkasan Penutup
Setelah mempelajari contoh soal dan jawaban invers matriks ordo 2×2, Anda kini memiliki pemahaman yang lebih baik tentang cara menentukan invers matriks dan penerapannya dalam menyelesaikan sistem persamaan linear. Ingatlah untuk memahami konsep dasar dan rumus dengan baik, dan jangan ragu untuk berlatih dengan berbagai contoh soal. Dengan latihan yang cukup, Anda akan semakin mahir dalam menyelesaikan masalah yang melibatkan invers matriks. Selamat belajar!





