Contoh soal mean data kelompok dan jawabannya – Pernahkah Anda bertanya-tanya bagaimana cara menghitung rata-rata dari data yang dikelompokkan? Misalnya, bagaimana menentukan rata-rata nilai ujian siswa dalam suatu kelas jika nilai tersebut dikelompokkan dalam rentang tertentu? Nah, konsep mean data kelompok hadir untuk membantu Anda! Mean data kelompok merupakan cara untuk menghitung rata-rata data yang telah dikelompokkan ke dalam kelas-kelas interval.
Dalam artikel ini, kita akan menjelajahi lebih dalam tentang mean data kelompok, mulai dari pengertian, rumus, langkah-langkah perhitungan, hingga contoh soal dan jawabannya. Dengan memahami konsep ini, Anda akan mampu menganalisis data kelompok dengan lebih mudah dan akurat.
Pengertian Mean Data Kelompok
Mean data kelompok, juga dikenal sebagai rata-rata data kelompok, adalah ukuran pusat kecenderungan yang digunakan untuk menentukan nilai tengah dari suatu kumpulan data yang dibagi menjadi beberapa kelompok atau kelas. Nilai mean data kelompok ini mewakili nilai tengah keseluruhan data, meskipun data tersebut dikelompokkan berdasarkan rentang nilai tertentu.
Contoh Mean Data Kelompok
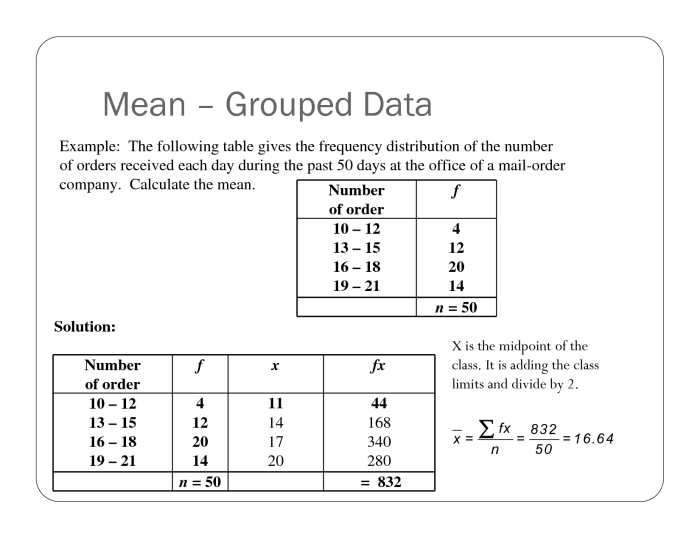
Misalnya, dalam sebuah kelas terdapat 50 siswa dengan nilai ujian yang dikelompokkan berdasarkan rentang nilai seperti pada tabel berikut:
| Rentang Nilai | Frekuensi |
|---|---|
| 60-69 | 10 |
| 70-79 | 15 |
| 80-89 | 18 |
| 90-99 | 7 |
Untuk menghitung mean data kelompok ini, kita perlu menentukan nilai tengah setiap rentang nilai, mengalikannya dengan frekuensi, menjumlahkan hasil perkalian tersebut, dan membaginya dengan jumlah total frekuensi.
Perbedaan Mean Data Kelompok dan Mean Data Tunggal
Mean data kelompok berbeda dengan mean data tunggal. Mean data tunggal menghitung nilai tengah dari data yang tidak dikelompokkan, sedangkan mean data kelompok menghitung nilai tengah dari data yang sudah dikelompokkan berdasarkan rentang nilai tertentu.
| Karakteristik | Mean Data Tunggal | Mean Data Kelompok |
|---|---|---|
| Data | Data tidak dikelompokkan | Data dikelompokkan berdasarkan rentang nilai |
| Rumus | ∑x / n | ∑(fi * xi) / ∑fi |
| Kegunaan | Menghitung nilai tengah dari data yang tidak dikelompokkan | Menghitung nilai tengah dari data yang dikelompokkan berdasarkan rentang nilai |
Perbedaan utama terletak pada cara pengolahan data. Mean data tunggal menggunakan setiap nilai data secara individual, sedangkan mean data kelompok menggunakan nilai tengah setiap kelompok sebagai representasi dari data dalam kelompok tersebut.
Rumus Mean Data Kelompok
Rumus mean data kelompok digunakan untuk menghitung rata-rata data yang telah dikelompokkan dalam tabel distribusi frekuensi. Rumus ini mempertimbangkan nilai tengah setiap kelas interval dan frekuensi kelas tersebut.
Rumus Mean Data Kelompok, Contoh soal mean data kelompok dan jawabannya
Rumus mean data kelompok adalah:
Mean = (∑(fi * xi)) / ∑fi
Keterangan:
- Mean: Rata-rata data kelompok
- fi: Frekuensi kelas ke-i
- xi: Nilai tengah kelas ke-i
- ∑: Simbol penjumlahan
Contoh Penggunaan Rumus Mean Data Kelompok
Misalnya, kita memiliki data nilai ujian 20 siswa yang dikelompokkan dalam tabel distribusi frekuensi berikut:
| Nilai Ujian | Frekuensi (fi) |
|---|---|
| 60 – 69 | 3 |
| 70 – 79 | 6 |
| 80 – 89 | 8 |
| 90 – 99 | 3 |
Untuk menghitung mean data kelompok, kita perlu menghitung nilai tengah setiap kelas interval (xi) dan mengalikannya dengan frekuensi kelas (fi).
| Nilai Ujian | Frekuensi (fi) | Nilai Tengah (xi) | fi * xi |
|---|---|---|---|
| 60 – 69 | 3 | 64.5 | 193.5 |
| 70 – 79 | 6 | 74.5 | 447 |
| 80 – 89 | 8 | 84.5 | 676 |
| 90 – 99 | 3 | 94.5 | 283.5 |
Selanjutnya, kita jumlahkan semua hasil perkalian fi * xi dan jumlahkan semua frekuensi (fi).
∑(fi * xi) = 193.5 + 447 + 676 + 283.5 = 1600
∑fi = 3 + 6 + 8 + 3 = 20
Maka, mean data kelompok adalah:
Mean = (∑(fi * xi)) / ∑fi = 1600 / 20 = 80
Jadi, rata-rata nilai ujian 20 siswa tersebut adalah 80.
Langkah-langkah Menghitung Mean Data Kelompok
Menghitung mean data kelompok, atau rata-rata, merupakan cara yang umum untuk mendapatkan gambaran umum dari kumpulan data yang dibagi menjadi beberapa kelompok. Langkah-langkah yang digunakan untuk menghitung mean data kelompok ini cukup sederhana dan mudah dipahami.
Langkah-langkah Menghitung Mean Data Kelompok
Berikut adalah langkah-langkah yang dapat Anda ikuti untuk menghitung mean data kelompok:
- Tentukan Jumlah Data dalam Setiap Kelompok: Langkah pertama adalah menentukan jumlah data atau frekuensi dalam setiap kelompok. Hal ini penting untuk menentukan bobot setiap kelompok dalam perhitungan mean.
- Tentukan Nilai Tengah Setiap Kelompok: Nilai tengah setiap kelompok, atau titik tengah, adalah nilai yang mewakili seluruh data dalam kelompok tersebut. Untuk menentukan nilai tengah, Anda dapat menggunakan rumus: Nilai Tengah = (Batas Atas + Batas Bawah) / 2. Contohnya, jika kelompok pertama memiliki batas bawah 10 dan batas atas 20, maka nilai tengahnya adalah (10 + 20) / 2 = 15.
- Kalikan Nilai Tengah dengan Frekuensi Setiap Kelompok: Setelah menentukan nilai tengah setiap kelompok, kalikan nilai tengah tersebut dengan frekuensi kelompok. Hasil perkalian ini akan memberikan jumlah data dalam kelompok tersebut.
- Jumlahkan Hasil Perkalian Setiap Kelompok: Jumlahkan semua hasil perkalian yang diperoleh dari langkah sebelumnya. Jumlah ini akan memberikan total data dalam semua kelompok.
- Jumlahkan Frekuensi Semua Kelompok: Jumlahkan semua frekuensi dari setiap kelompok. Ini akan memberikan total data dalam semua kelompok.
- Bagi Total Data dengan Total Frekuensi: Bagi total data yang diperoleh dari langkah 4 dengan total frekuensi yang diperoleh dari langkah 5. Hasilnya adalah mean data kelompok.
Sebagai contoh, mari kita perhatikan data kelompok berikut:
| Kelompok | Batas Bawah | Batas Atas | Frekuensi |
|---|---|---|---|
| 1 | 10 | 20 | 5 |
| 2 | 20 | 30 | 10 |
| 3 | 30 | 40 | 15 |
Berikut adalah langkah-langkah menghitung mean data kelompok menggunakan data di atas:
- Tentukan Jumlah Data dalam Setiap Kelompok: Frekuensi setiap kelompok sudah diberikan dalam tabel, yaitu 5, 10, dan 15.
- Tentukan Nilai Tengah Setiap Kelompok:
- Kelompok 1: (10 + 20) / 2 = 15
- Kelompok 2: (20 + 30) / 2 = 25
- Kelompok 3: (30 + 40) / 2 = 35
- Kalikan Nilai Tengah dengan Frekuensi Setiap Kelompok:
- Kelompok 1: 15 * 5 = 75
- Kelompok 2: 25 * 10 = 250
- Kelompok 3: 35 * 15 = 525
- Jumlahkan Hasil Perkalian Setiap Kelompok: 75 + 250 + 525 = 850
- Jumlahkan Frekuensi Semua Kelompok: 5 + 10 + 15 = 30
- Bagi Total Data dengan Total Frekuensi: 850 / 30 = 28.33
Jadi, mean data kelompok tersebut adalah 28.33.
Contoh Soal Mean Data Kelompok
Menghitung mean data kelompok adalah cara yang efisien untuk menemukan nilai rata-rata dari kumpulan data yang terbagi dalam beberapa kelompok. Setiap kelompok memiliki nilai tengah, frekuensi, dan rentang data sendiri. Dengan menggunakan rumus mean data kelompok, kita dapat memperoleh nilai rata-rata keseluruhan data dengan mudah. Untuk memahami lebih lanjut tentang mean data kelompok, mari kita bahas beberapa contoh soal berikut:
Contoh Soal Mean Data Kelompok
Berikut adalah tiga contoh soal mean data kelompok dengan tingkat kesulitan yang berbeda, disertai dengan jawaban lengkap dan detail untuk membantu Anda memahami konsepnya:
| No | Soal | Jawaban |
|---|---|---|
| 1 | Sebuah toko buku mencatat penjualan buku selama seminggu. Data penjualan buku dikelompokkan berdasarkan jenis buku seperti berikut:
| Jenis Buku | Jumlah Buku Terjual | Hitunglah mean penjualan buku selama seminggu! |
Untuk menghitung mean penjualan buku, kita perlu menentukan nilai tengah (xi) dari setiap jenis buku. Karena tidak diketahui rentang data, kita asumsikan bahwa semua buku dalam satu jenis memiliki nilai tengah yang sama.
| Jenis Buku | Jumlah Buku Terjual (fi) | Nilai Tengah (xi) | xifi | Kemudian, kita jumlahkan semua nilai xifi dan bagi dengan jumlah total buku terjual (∑fi). ∑xifi = 2500 + 900 + 400 = 3800 Mean penjualan buku = ∑xifi / ∑fi = 3800 / 100 = 38 Jadi, mean penjualan buku selama seminggu adalah 38 buku. |
| 2 | Suatu kelas terdiri dari 40 siswa. Data nilai ujian matematika mereka dikelompokkan sebagai berikut:
| Interval Nilai | Frekuensi (fi) | Hitunglah mean nilai ujian matematika kelas tersebut! |
Untuk menghitung mean nilai ujian matematika, kita perlu menentukan nilai tengah (xi) dari setiap interval nilai.
| Interval Nilai | Frekuensi (fi) | Nilai Tengah (xi) | xifi | Kemudian, kita jumlahkan semua nilai xifi dan bagi dengan jumlah total frekuensi (∑fi). ∑xifi = 322.5 + 745 + 1267.5 + 945 = 3280 Mean nilai ujian matematika = ∑xifi / ∑fi = 3280 / 40 = 82 Jadi, mean nilai ujian matematika kelas tersebut adalah 82. |
| 3 | Sebuah perusahaan mencatat data produksi selama 5 hari. Data produksi dikelompokkan berdasarkan jenis produk seperti berikut:
| Jenis Produk | Jumlah Produksi (fi) | Nilai Tengah (xi) | Hitunglah mean produksi perusahaan selama 5 hari! |
Kita sudah diberikan nilai tengah (xi) dari setiap jenis produk, sehingga kita dapat langsung menghitung mean produksi dengan menggunakan rumus mean data kelompok.
∑xifi = (10 x 100) + (15 x 150) + (20 x 200) = 1000 + 2250 + 4000 = 7250 Mean produksi = ∑xifi / ∑fi = 7250 / 450 = 16.11 Jadi, mean produksi perusahaan selama 5 hari adalah 16.11 unit. |
Aplikasi Mean Data Kelompok
Mean data kelompok adalah konsep statistik yang sangat berguna dalam berbagai bidang, seperti pendidikan, ekonomi, dan sosial. Mean data kelompok membantu kita memahami tren dan pola dalam data yang terkelompokkan, sehingga kita dapat membuat keputusan yang lebih tepat berdasarkan informasi yang tersedia.
Pendidikan
Mean data kelompok dapat digunakan untuk menganalisis nilai ujian siswa dalam suatu kelas. Misalnya, jika kita memiliki data nilai ujian siswa di kelas A, kelas B, dan kelas C, kita dapat menghitung mean nilai ujian untuk setiap kelas. Dengan membandingkan mean nilai ujian antar kelas, kita dapat mengetahui kelas mana yang memiliki kinerja akademik yang lebih baik.
- Mean data kelompok membantu guru mengidentifikasi kelas yang membutuhkan perhatian khusus, misalnya kelas dengan nilai rata-rata yang lebih rendah. Guru dapat kemudian fokus memberikan bimbingan dan pembelajaran tambahan untuk membantu siswa di kelas tersebut.
- Mean data kelompok juga dapat digunakan untuk memantau perkembangan belajar siswa dari waktu ke waktu. Misalnya, guru dapat menghitung mean nilai ujian siswa di semester pertama dan semester kedua. Jika mean nilai ujian di semester kedua lebih tinggi daripada di semester pertama, ini menunjukkan bahwa siswa telah menunjukkan peningkatan dalam belajar.
Ekonomi
Mean data kelompok dapat digunakan untuk menganalisis pendapatan rata-rata penduduk di berbagai wilayah. Misalnya, kita dapat menghitung mean pendapatan rata-rata penduduk di kota A, kota B, dan kota C. Dengan membandingkan mean pendapatan rata-rata antar kota, kita dapat mengetahui kota mana yang memiliki tingkat kesejahteraan ekonomi yang lebih tinggi.
- Mean data kelompok membantu pemerintah dalam menentukan kebijakan ekonomi yang tepat, misalnya dengan memberikan bantuan atau insentif kepada wilayah dengan tingkat kesejahteraan ekonomi yang lebih rendah.
- Mean data kelompok juga dapat digunakan untuk menganalisis tingkat inflasi di berbagai sektor ekonomi. Misalnya, kita dapat menghitung mean inflasi di sektor makanan, sektor energi, dan sektor transportasi. Dengan membandingkan mean inflasi antar sektor, kita dapat mengetahui sektor mana yang mengalami kenaikan harga yang lebih tinggi.
Sosial
Mean data kelompok dapat digunakan untuk menganalisis tingkat kepuasan masyarakat terhadap layanan publik. Misalnya, kita dapat menghitung mean tingkat kepuasan masyarakat terhadap layanan kesehatan di berbagai daerah. Dengan membandingkan mean tingkat kepuasan antar daerah, kita dapat mengetahui daerah mana yang memiliki tingkat kepuasan masyarakat yang lebih tinggi terhadap layanan kesehatan.
- Mean data kelompok membantu pemerintah dalam meningkatkan kualitas layanan publik. Misalnya, jika mean tingkat kepuasan masyarakat terhadap layanan kesehatan di daerah A lebih rendah daripada di daerah B, pemerintah dapat fokus meningkatkan kualitas layanan kesehatan di daerah A.
- Mean data kelompok juga dapat digunakan untuk menganalisis tingkat kejahatan di berbagai wilayah. Misalnya, kita dapat menghitung mean tingkat kejahatan di kota A, kota B, dan kota C. Dengan membandingkan mean tingkat kejahatan antar kota, kita dapat mengetahui kota mana yang memiliki tingkat kejahatan yang lebih tinggi. Ini membantu polisi dalam mengalokasikan sumber daya mereka dengan lebih efektif.
Perbedaan Mean Data Kelompok dan Mean Data Tunggal: Contoh Soal Mean Data Kelompok Dan Jawabannya
Dalam statistika, mean merupakan ukuran tendensi sentral yang menunjukkan nilai rata-rata dari sekumpulan data. Mean dapat dihitung untuk data tunggal maupun data kelompok. Data tunggal merujuk pada data yang tidak dikelompokkan, sedangkan data kelompok merupakan data yang dikelompokkan berdasarkan interval kelas tertentu. Perbedaan mendasar antara mean data kelompok dan mean data tunggal terletak pada cara perhitungannya, yang dipengaruhi oleh bagaimana data tersebut disusun.
Perbedaan Rumus dan Cara Menghitung
Berikut tabel yang membandingkan rumus dan cara menghitung mean data kelompok dan mean data tunggal:
| Karakteristik | Mean Data Tunggal | Mean Data Kelompok |
|---|---|---|
| Rumus | X̄ = ΣX / n | X̄ = Σ(fi * xi) / Σfi |
| Keterangan |
|
|
| Cara Menghitung | Jumlahkan semua data, kemudian bagi dengan jumlah data. | Kalikan frekuensi setiap kelas dengan titik tengah kelasnya, kemudian jumlahkan hasil perkalian tersebut. Bagi hasil penjumlahan dengan jumlah frekuensi semua kelas. |
Contoh Soal
Berikut contoh soal yang menunjukkan perbedaan penggunaan mean data kelompok dan mean data tunggal:
Misalkan terdapat data nilai ujian matematika dari 10 siswa sebagai berikut:
- 70
- 80
- 75
- 85
- 90
- 75
- 80
- 85
- 90
- 75
Untuk menghitung mean data tunggal, kita dapat menggunakan rumus:
X̄ = ΣX / n
Dengan ΣX = 795 dan n = 10, maka mean data tunggal adalah:
X̄ = 795 / 10 = 79,5
Sekarang, misalkan data nilai ujian matematika tersebut dikelompokkan ke dalam interval kelas sebagai berikut:
| Interval Kelas | Frekuensi (fi) | Titik Tengah (xi) | fi * xi |
|---|---|---|---|
| 70 – 75 | 3 | 72,5 | 217,5 |
| 75 – 80 | 4 | 77,5 | 310 |
| 80 – 85 | 2 | 82,5 | 165 |
| 85 – 90 | 1 | 87,5 | 87,5 |
Untuk menghitung mean data kelompok, kita dapat menggunakan rumus:
X̄ = Σ(fi * xi) / Σfi
Dengan Σ(fi * xi) = 780 dan Σfi = 10, maka mean data kelompok adalah:
X̄ = 780 / 10 = 78
Dari contoh soal di atas, terlihat bahwa mean data tunggal dan mean data kelompok memiliki nilai yang berbeda. Hal ini dikarenakan cara perhitungannya yang berbeda, di mana mean data kelompok mempertimbangkan frekuensi setiap kelas.
Keuntungan dan Kerugian Mean Data Kelompok
Mean data kelompok, atau rata-rata data kelompok, merupakan salah satu ukuran pemusatan data yang berguna untuk menganalisis data yang dikelompokkan. Penggunaan mean data kelompok memiliki keuntungan dan kerugian yang perlu dipahami untuk memastikan interpretasi data yang tepat.
Keuntungan Mean Data Kelompok
Mean data kelompok menawarkan beberapa keuntungan dalam analisis data, terutama ketika bekerja dengan data yang terkelompokkan.
- Representasi Data yang Lebih Ringkas: Mean data kelompok memberikan gambaran singkat tentang pusat data dalam setiap kelompok. Ini memudahkan untuk membandingkan data antar kelompok, terutama jika jumlah data dalam setiap kelompok besar.
- Mudah Dihitung: Perhitungan mean data kelompok relatif mudah, bahkan untuk data yang besar. Hal ini membuat mean data kelompok menjadi alat yang praktis untuk analisis data.
- Stabilitas: Mean data kelompok cenderung lebih stabil dibandingkan dengan ukuran pemusatan lainnya, seperti median, karena dipengaruhi oleh semua nilai dalam kelompok.
Kerugian Mean Data Kelompok
Meskipun memiliki beberapa keuntungan, mean data kelompok juga memiliki beberapa kelemahan yang perlu diperhatikan.
- Dipengaruhi Oleh Outlier: Mean data kelompok sangat sensitif terhadap outlier, yaitu nilai data yang sangat jauh dari nilai lainnya. Outlier dapat memengaruhi mean data kelompok secara signifikan, sehingga tidak mencerminkan pusat data yang sebenarnya.
- Tidak Mewakili Distribusi Data: Mean data kelompok hanya menunjukkan pusat data, tetapi tidak memberikan informasi tentang sebaran data dalam kelompok. Data yang terdistribusi secara tidak merata, seperti data yang memiliki banyak outlier, tidak dapat digambarkan secara akurat oleh mean data kelompok.
- Tidak Sesuai untuk Data Kategorikal: Mean data kelompok tidak dapat digunakan untuk data kategorikal, seperti jenis kelamin atau warna. Data kategorikal tidak memiliki nilai numerik yang dapat dirata-ratakan.
Contoh Kasus Keuntungan dan Kerugian Mean Data Kelompok
Misalnya, dalam penelitian tentang tinggi badan siswa di suatu sekolah, mean data kelompok dapat digunakan untuk membandingkan tinggi badan siswa di kelas yang berbeda. Namun, jika ada beberapa siswa dengan tinggi badan yang sangat tinggi (outlier) di satu kelas, mean data kelompok untuk kelas tersebut akan terpengaruh, sehingga tidak mencerminkan tinggi badan rata-rata siswa di kelas tersebut secara akurat.
Contoh lain, jika kita ingin menganalisis pendapatan rata-rata penduduk di suatu kota berdasarkan tingkat pendidikan, mean data kelompok dapat digunakan untuk membandingkan pendapatan rata-rata penduduk dengan pendidikan tinggi dan pendidikan rendah. Namun, mean data kelompok tidak dapat memberikan informasi tentang sebaran pendapatan dalam setiap kelompok pendidikan, sehingga kita tidak dapat mengetahui apakah pendapatan penduduk dengan pendidikan tinggi terdistribusi secara merata atau tidak.
Cara Memilih Metode Perhitungan Mean yang Tepat
Menghitung mean atau rata-rata adalah langkah penting dalam analisis data. Namun, memilih metode perhitungan mean yang tepat sangatlah krusial untuk mendapatkan hasil yang akurat dan representatif. Terdapat dua metode utama perhitungan mean, yaitu mean data tunggal dan mean data kelompok.
Contoh soal mean data kelompok dan jawabannya seringkali melibatkan pengelompokan data berdasarkan kategori tertentu. Misalnya, untuk menghitung rata-rata tinggi badan siswa di kelas, kita bisa mengelompokkan mereka berdasarkan jenis kelamin. Nah, dalam contoh soal ini, kita bisa menemukan kaitan dengan contoh soal satuan tidak baku kelas 1 SD seperti contoh soal satuan tidak baku kelas 1 sd yang melibatkan penggunaan satuan seperti “gelas” atau “sendok” untuk mengukur volume.
Begitu pula, dalam contoh soal mean data kelompok, kita bisa menggunakan satuan tidak baku untuk mengelompokkan data, seperti “banyaknya siswa” atau “jumlah buku” dalam satu kelompok. Dengan demikian, contoh soal mean data kelompok dan jawabannya bisa dikaitkan dengan materi satuan tidak baku yang dipelajari di kelas 1 SD.
Jenis Data dan Metode Mean yang Sesuai
Pemilihan metode perhitungan mean bergantung pada jenis data yang tersedia.
- Mean Data Tunggal: Digunakan ketika data yang tersedia berupa nilai tunggal, misalnya tinggi badan siswa, nilai ujian, atau suhu ruangan.
- Mean Data Kelompok: Digunakan ketika data yang tersedia berupa kelompok data, misalnya skor ujian siswa dalam beberapa mata pelajaran, tinggi badan siswa dalam beberapa kelas, atau suhu ruangan dalam beberapa hari.
Contoh Data dan Metode Mean yang Sesuai
Berikut contoh data yang sesuai untuk penggunaan mean data kelompok dan mean data tunggal:
- Mean Data Kelompok: Misalnya, data nilai ujian siswa dalam tiga mata pelajaran: Matematika, Bahasa Indonesia, dan IPA. Setiap mata pelajaran memiliki nilai yang berbeda-beda, sehingga data ini merupakan data kelompok.
- Mean Data Tunggal: Misalnya, data tinggi badan seorang siswa. Data ini merupakan data tunggal karena hanya mewakili satu individu.
Faktor-Faktor yang Perlu Dipertimbangkan dalam Memilih Metode Mean
Selain jenis data, beberapa faktor lain perlu dipertimbangkan dalam memilih metode perhitungan mean, yaitu:
- Tujuan Analisis: Apakah tujuan analisis adalah untuk mengetahui nilai rata-rata keseluruhan data atau nilai rata-rata setiap kelompok data?
- Sifat Data: Apakah data yang tersedia bersifat numerik, kategorikal, atau ordinal?
- Distribusi Data: Apakah data terdistribusi normal atau tidak normal?
Menganalisis Data Kelompok dengan Mean
Mean data kelompok merupakan alat yang berguna untuk memahami dan menganalisis data yang terbagi dalam beberapa kelompok. Mean, atau rata-rata, memberikan gambaran umum tentang nilai tengah dari setiap kelompok data.
Cara Menggunakan Mean Data Kelompok untuk Menganalisis Data
Mean data kelompok membantu kita melihat tren, perbandingan, dan pola di antara kelompok-kelompok data. Dengan menghitung mean untuk setiap kelompok, kita dapat:
- Membandingkan nilai tengah: Melihat perbedaan signifikansi antara nilai tengah dari setiap kelompok data.
- Mengenali tren: Menentukan apakah ada tren yang jelas dalam data, seperti peningkatan atau penurunan nilai mean dari satu kelompok ke kelompok lainnya.
- Menganalisis efek variabel: Memahami bagaimana variabel independen mempengaruhi variabel dependen dengan melihat perubahan mean pada kelompok-kelompok data.
Contoh Analisis Data Kelompok dengan Mean
Misalnya, kita ingin menganalisis skor ujian matematika dari siswa di tiga kelas berbeda.
| Kelas | Skor Ujian | Mean |
|---|---|---|
| Kelas A | 75, 80, 85, 90, 95 | 85 |
| Kelas B | 65, 70, 75, 80, 85 | 75 |
| Kelas C | 85, 90, 95, 100, 105 | 95 |
Dari tabel di atas, kita dapat melihat bahwa:
- Kelas C memiliki skor rata-rata tertinggi (95), diikuti oleh Kelas A (85), dan Kelas B (75).
- Ada perbedaan signifikan antara nilai mean dari setiap kelas, menunjukkan bahwa ada perbedaan dalam performa siswa di setiap kelas.
Informasi yang Diperoleh dari Analisis Data Kelompok dengan Mean
Melalui analisis data kelompok dengan mean, kita dapat memperoleh informasi yang berharga, seperti:
- Perbandingan antar kelompok: Membandingkan nilai tengah dari setiap kelompok data untuk melihat perbedaan signifikansi.
- Tren dan pola: Mengidentifikasi tren atau pola dalam data, seperti peningkatan atau penurunan nilai mean dari satu kelompok ke kelompok lainnya.
- Efek variabel: Memahami bagaimana variabel independen mempengaruhi variabel dependen dengan melihat perubahan mean pada kelompok-kelompok data.
- Informasi tentang distribusi data: Meskipun mean tidak memberikan informasi lengkap tentang distribusi data, ia dapat memberikan gambaran umum tentang kecenderungan data.
Interpretasi Hasil Mean Data Kelompok
Setelah menghitung mean data kelompok, langkah selanjutnya adalah menginterpretasikan hasilnya. Interpretasi ini penting untuk memahami makna dari nilai mean dan bagaimana nilai tersebut berkaitan dengan data keseluruhan.
Cara Menginterpretasikan Hasil Mean Data Kelompok
Menginterpretasikan hasil mean data kelompok berarti memahami apa yang ditunjukkan oleh nilai mean dalam konteks data yang dianalisis. Berikut beberapa langkah yang dapat membantu:
- Perhatikan skala data: Apakah data dalam skala interval, rasio, ordinal, atau nominal? Skala data akan memengaruhi cara kita menginterpretasikan mean. Misalnya, mean skor ujian yang berkisar antara 0-100 akan berbeda interpretasinya dengan mean nilai rata-rata pendapatan yang dalam skala jutaan.
- Bandingkan dengan mean kelompok lain: Jika ada beberapa kelompok data, bandingkan mean dari masing-masing kelompok. Perbedaan mean antar kelompok dapat memberikan informasi tentang perbedaan karakteristik atau tren antar kelompok.
- Perhatikan variabilitas data: Mean saja tidak cukup untuk menggambarkan data sepenuhnya. Variabilitas data, seperti standar deviasi, juga penting untuk dipertimbangkan. Jika variabilitas tinggi, mean mungkin tidak mewakili data secara akurat karena adanya nilai ekstrem.
- Pertimbangkan konteks data: Interpretasi mean harus dilakukan dalam konteks data. Apa yang diukur oleh data? Siapa populasi yang diwakili oleh data? Informasi ini akan membantu kita memahami arti dari mean.
Contoh Hasil Mean Data Kelompok dan Interpretasinya
Misalnya, kita ingin mengetahui mean skor ujian matematika di dua kelas berbeda. Hasilnya menunjukkan bahwa mean skor kelas A adalah 75, sedangkan mean skor kelas B adalah 80.
Berdasarkan data ini, kita dapat menginterpretasikan bahwa secara umum, siswa di kelas B memiliki kinerja yang lebih baik dalam ujian matematika dibandingkan dengan siswa di kelas A. Namun, kita perlu mempertimbangkan faktor lain seperti variabilitas skor di setiap kelas. Jika variabilitas skor di kelas B tinggi, maka perbedaan mean mungkin tidak terlalu signifikan.
Faktor-Faktor yang Perlu Dipertimbangkan dalam Menginterpretasikan Hasil Mean Data Kelompok
- Ukuran sampel: Mean dari sampel yang kecil mungkin tidak selalu mewakili populasi secara akurat. Semakin besar ukuran sampel, semakin akurat mean sebagai representasi populasi.
- Metode pengumpulan data: Cara data dikumpulkan dapat memengaruhi hasil mean. Misalnya, jika data dikumpulkan melalui survei, bias dalam desain survei dapat memengaruhi hasil mean.
- Tujuan analisis: Tujuan analisis akan memengaruhi cara kita menginterpretasikan mean. Apakah kita ingin membandingkan kelompok, mengidentifikasi tren, atau menguji hipotesis? Tujuan analisis akan menentukan apa yang dicari dalam data.
Kesimpulan Akhir
Memahami cara menghitung mean data kelompok membuka pintu bagi Anda untuk menganalisis data yang lebih kompleks dan beragam. Dengan kemampuan ini, Anda dapat memperoleh wawasan yang lebih dalam tentang berbagai fenomena di sekitar kita, baik di bidang pendidikan, ekonomi, sosial, dan lain sebagainya.






