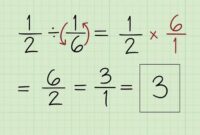Contoh soal bilangan aritmatika – Bilangan aritmatika merupakan konsep dasar dalam matematika yang sering kita temui dalam kehidupan sehari-hari. Mulai dari menghitung uang jajan, membagi kue, hingga menentukan jarak tempuh, bilangan aritmatika berperan penting dalam menyelesaikan berbagai masalah.
Dalam artikel ini, kita akan menjelajahi dunia bilangan aritmatika melalui contoh-contoh soal yang menarik dan mudah dipahami. Siapkan diri Anda untuk memahami konsep dasar, sifat-sifat, dan operasi bilangan aritmatika, serta penerapannya dalam berbagai bidang kehidupan.
Pengertian Bilangan Aritmatika
Bilangan aritmatika adalah jenis bilangan yang sering kita jumpai dalam kehidupan sehari-hari. Sederhananya, bilangan aritmatika adalah bilangan yang dapat dijumlahkan, dikurangkan, dikalikan, dan dibagi. Bilangan ini termasuk bilangan bulat, pecahan, dan desimal, dan berperan penting dalam berbagai bidang seperti matematika, ilmu pengetahuan, dan teknologi.
Contoh Bilangan Aritmatika
Berikut beberapa contoh bilangan aritmatika dan karakteristiknya:
- Bilangan bulat: Bilangan bulat adalah bilangan yang tidak memiliki pecahan atau desimal. Contohnya: -3, -2, -1, 0, 1, 2, 3, dan seterusnya. Karakteristiknya adalah bilangan bulat dapat diurutkan dan dapat dijumlahkan, dikurangkan, dikalikan, dan dibagi (kecuali dibagi nol).
- Pecahan: Pecahan adalah bilangan yang ditulis dalam bentuk a/b, dimana a dan b adalah bilangan bulat dan b tidak sama dengan nol. Contohnya: 1/2, 3/4, 5/6. Karakteristiknya adalah pecahan dapat disederhanakan, dijumlahkan, dikurangkan, dikalikan, dan dibagi.
- Desimal: Desimal adalah bilangan yang menggunakan tanda koma (,) untuk memisahkan bagian bulat dan bagian pecahan. Contohnya: 2,5, 3,14, 0,75. Karakteristiknya adalah desimal dapat diubah ke bentuk pecahan dan sebaliknya.
Perbedaan Bilangan Aritmatika dengan Jenis Bilangan Lainnya
Bilangan aritmatika memiliki perbedaan dengan jenis bilangan lainnya seperti bilangan bulat, bilangan rasional, dan bilangan irasional.
- Bilangan bulat: Bilangan bulat adalah subset dari bilangan aritmatika. Bilangan bulat hanya mencakup bilangan positif, negatif, dan nol, sedangkan bilangan aritmatika mencakup semua bilangan bulat, pecahan, dan desimal.
- Bilangan rasional: Bilangan rasional adalah bilangan yang dapat dinyatakan sebagai pecahan a/b, dimana a dan b adalah bilangan bulat dan b tidak sama dengan nol. Bilangan aritmatika mencakup semua bilangan rasional, tetapi tidak mencakup semua bilangan irasional.
- Bilangan irasional: Bilangan irasional adalah bilangan yang tidak dapat dinyatakan sebagai pecahan a/b. Contohnya adalah akar kuadrat dari 2 (√2) dan pi (π). Bilangan irasional tidak termasuk dalam bilangan aritmatika.
Sifat-sifat Bilangan Aritmatika: Contoh Soal Bilangan Aritmatika
Bilangan aritmatika merupakan jenis bilangan yang paling dasar dan sering kita gunakan dalam kehidupan sehari-hari. Bilangan aritmatika memiliki sifat-sifat unik yang membantu kita dalam memahami dan menyelesaikan berbagai operasi matematika. Sifat-sifat ini menjadi landasan dalam berbagai bidang, seperti aljabar, kalkulus, dan bahkan pemrograman komputer.
Sifat-sifat Dasar Bilangan Aritmatika
Sifat-sifat dasar bilangan aritmatika membantu kita dalam memahami bagaimana bilangan-bilangan tersebut berinteraksi satu sama lain. Berikut adalah beberapa sifat dasar yang perlu kita pahami:
- Sifat Komutatif: Dalam penjumlahan dan perkalian, urutan operasi tidak memengaruhi hasil. Artinya, a + b = b + a dan a × b = b × a.
- Sifat Asosiatif: Dalam penjumlahan dan perkalian, cara pengelompokan bilangan tidak memengaruhi hasil. Artinya, (a + b) + c = a + (b + c) dan (a × b) × c = a × (b × c).
- Sifat Distributif: Perkalian dapat didistribusikan terhadap penjumlahan atau pengurangan. Artinya, a × (b + c) = (a × b) + (a × c).
- Identitas Penjumlahan: Penjumlahan bilangan dengan nol menghasilkan bilangan itu sendiri. Artinya, a + 0 = a.
- Identitas Perkalian: Perkalian bilangan dengan satu menghasilkan bilangan itu sendiri. Artinya, a × 1 = a.
- Invers Penjumlahan: Setiap bilangan memiliki invers penjumlahan, yaitu bilangan yang jika dijumlahkan dengan bilangan tersebut menghasilkan nol. Artinya, a + (-a) = 0.
- Invers Perkalian: Setiap bilangan (kecuali nol) memiliki invers perkalian, yaitu bilangan yang jika dikalikan dengan bilangan tersebut menghasilkan satu. Artinya, a × (1/a) = 1.
Contoh Penerapan Sifat-sifat Bilangan Aritmatika
Sifat-sifat bilangan aritmatika dapat diterapkan dalam berbagai soal matematika, seperti:
- Soal Penjumlahan: Misalkan kita ingin menjumlahkan 5 + 7 + 3. Dengan sifat asosiatif, kita dapat mengelompokkan bilangan-bilangan tersebut: (5 + 7) + 3 = 12 + 3 = 15. Kita juga dapat menggunakan sifat komutatif untuk mengubah urutan penjumlahan: 5 + 7 + 3 = 5 + 3 + 7 = 8 + 7 = 15.
- Soal Perkalian: Misalkan kita ingin mengalikan 2 × 5 × 4. Dengan sifat asosiatif, kita dapat mengelompokkan bilangan-bilangan tersebut: (2 × 5) × 4 = 10 × 4 = 40. Kita juga dapat menggunakan sifat komutatif untuk mengubah urutan perkalian: 2 × 5 × 4 = 2 × 4 × 5 = 8 × 5 = 40.
- Soal Distributif: Misalkan kita ingin menghitung 3 × (4 + 2). Dengan sifat distributif, kita dapat mengalikan 3 dengan masing-masing bilangan di dalam kurung: 3 × (4 + 2) = (3 × 4) + (3 × 2) = 12 + 6 = 18.
Tabel Sifat-sifat Bilangan Aritmatika
| Sifat | Rumus | Contoh |
|---|---|---|
| Komutatif Penjumlahan | a + b = b + a | 2 + 3 = 3 + 2 |
| Komutatif Perkalian | a × b = b × a | 4 × 5 = 5 × 4 |
| Asosiatif Penjumlahan | (a + b) + c = a + (b + c) | (2 + 3) + 4 = 2 + (3 + 4) |
| Asosiatif Perkalian | (a × b) × c = a × (b × c) | (2 × 3) × 4 = 2 × (3 × 4) |
| Distributif | a × (b + c) = (a × b) + (a × c) | 3 × (2 + 4) = (3 × 2) + (3 × 4) |
| Identitas Penjumlahan | a + 0 = a | 5 + 0 = 5 |
| Identitas Perkalian | a × 1 = a | 7 × 1 = 7 |
| Invers Penjumlahan | a + (-a) = 0 | 6 + (-6) = 0 |
| Invers Perkalian | a × (1/a) = 1 | 8 × (1/8) = 1 |
Operasi pada Bilangan Aritmatika
Bilangan aritmatika adalah dasar dari matematika, dan operasi dasar pada bilangan aritmatika adalah fondasi untuk menyelesaikan berbagai macam masalah matematika. Operasi dasar ini meliputi penjumlahan, pengurangan, perkalian, dan pembagian. Keempat operasi ini saling terkait dan dapat digunakan dalam kombinasi untuk menyelesaikan masalah yang lebih kompleks.
Penjumlahan
Penjumlahan adalah operasi dasar yang menggabungkan dua atau lebih bilangan untuk menghasilkan jumlah total. Simbol “+” digunakan untuk mewakili penjumlahan. Contohnya, 2 + 3 = 5, di mana 2 dan 3 adalah bilangan yang dijumlahkan, dan 5 adalah jumlah totalnya.
Pengurangan
Pengurangan adalah operasi dasar yang mengurangi satu bilangan dari bilangan lainnya. Simbol “-” digunakan untuk mewakili pengurangan. Contohnya, 5 – 2 = 3, di mana 5 adalah bilangan yang dikurangi, 2 adalah bilangan yang dikurangkan, dan 3 adalah selisihnya.
Perkalian
Perkalian adalah operasi dasar yang mengulang penjumlahan suatu bilangan sebanyak bilangan lainnya. Simbol “×” atau “*” digunakan untuk mewakili perkalian. Contohnya, 3 × 4 = 12, di mana 3 dikalikan dengan 4, dan 12 adalah hasil perkaliannya.
Pembagian
Pembagian adalah operasi dasar yang membagi suatu bilangan menjadi beberapa bagian yang sama. Simbol “÷” atau “/” digunakan untuk mewakili pembagian. Contohnya, 12 ÷ 4 = 3, di mana 12 dibagi dengan 4, dan 3 adalah hasilnya.
Contoh Soal dan Penyelesaian
- Penjumlahan: Misalkan Anda memiliki 5 apel dan teman Anda memberikan 3 apel lagi. Berapa total apel yang Anda miliki? Untuk menyelesaikan masalah ini, Anda dapat menjumlahkan 5 dan 3: 5 + 3 = 8. Jadi, Anda memiliki total 8 apel.
- Pengurangan: Misalkan Anda memiliki 10 permen dan Anda memberikan 4 permen kepada adik Anda. Berapa sisa permen yang Anda miliki? Untuk menyelesaikan masalah ini, Anda dapat mengurangi 4 dari 10: 10 – 4 = 6. Jadi, Anda memiliki sisa 6 permen.
- Perkalian: Misalkan Anda membeli 3 kotak pensil, dan setiap kotak berisi 12 pensil. Berapa total pensil yang Anda miliki? Untuk menyelesaikan masalah ini, Anda dapat mengalikan 3 dengan 12: 3 × 12 = 36. Jadi, Anda memiliki total 36 pensil.
- Pembagian: Misalkan Anda memiliki 24 kue dan ingin membaginya secara merata kepada 6 teman Anda. Berapa kue yang akan diterima setiap teman Anda? Untuk menyelesaikan masalah ini, Anda dapat membagi 24 dengan 6: 24 ÷ 6 = 4. Jadi, setiap teman Anda akan menerima 4 kue.
Algoritma dalam Operasi Bilangan Aritmatika
Algoritma adalah serangkaian langkah yang sistematis untuk menyelesaikan suatu masalah. Dalam operasi bilangan aritmatika, algoritma dapat digunakan untuk menyelesaikan masalah yang lebih kompleks. Misalnya, algoritma perkalian panjang dapat digunakan untuk mengalikan dua bilangan besar. Algoritma pembagian panjang dapat digunakan untuk membagi dua bilangan besar. Algoritma ini membantu kita untuk menyelesaikan masalah dengan cara yang terstruktur dan efisien.
Barisan Aritmatika
Barisan aritmatika adalah barisan bilangan yang memiliki selisih yang sama antara dua suku berurutan. Selisih ini disebut beda. Dengan kata lain, setiap suku diperoleh dengan menambahkan beda ke suku sebelumnya.
Pengertian Barisan Aritmatika
Barisan aritmatika merupakan suatu barisan bilangan yang memiliki pola tertentu, yaitu selisih antara dua suku yang berdekatan selalu sama. Selisih ini disebut beda.
Rumus Umum Barisan Aritmatika
Rumus umum untuk menentukan suku ke-n (Un) dalam barisan aritmatika adalah:
Un = a + (n – 1)b
Dimana:
– Un adalah suku ke-n
– a adalah suku pertama
– b adalah beda
– n adalah nomor suku
Contoh Barisan Aritmatika
Misalnya, barisan bilangan 2, 5, 8, 11, 14… adalah barisan aritmatika. Suku pertama (a) adalah 2, beda (b) adalah 3, dan suku ke-5 (U5) adalah 14.
Menentukan Suku Pertama, Beda, dan Suku ke-n
Untuk menentukan suku pertama, beda, dan suku ke-n dalam barisan aritmatika, kita dapat menggunakan rumus umum dan informasi yang diberikan.
Tabel Contoh Barisan Aritmatika
Berikut adalah tabel yang menunjukkan beberapa contoh barisan aritmatika dan rumus yang digunakan untuk menghitung suku ke-n:
| Barisan Aritmatika | Suku Pertama (a) | Beda (b) | Rumus Suku ke-n (Un) |
|---|---|---|---|
| 2, 5, 8, 11, 14… | 2 | 3 | Un = 2 + (n – 1)3 |
| -3, 1, 5, 9, 13… | -3 | 4 | Un = -3 + (n – 1)4 |
| 10, 7, 4, 1, -2… | 10 | -3 | Un = 10 + (n – 1)(-3) |
Penerapan Bilangan Aritmatika dalam Kehidupan Sehari-hari

Bilangan aritmatika merupakan dasar dari matematika yang sering kita gunakan dalam kehidupan sehari-hari tanpa disadari. Konsep-konsep seperti penjumlahan, pengurangan, perkalian, dan pembagian menjadi alat penting untuk menyelesaikan berbagai masalah yang kita hadapi. Dari mengatur keuangan pribadi hingga memahami data ilmiah, bilangan aritmatika berperan penting dalam membantu kita memahami dan menavigasi dunia di sekitar kita.
Keuangan
Dalam dunia keuangan, bilangan aritmatika sangat vital. Kita menggunakannya untuk menghitung pengeluaran, menabung, dan merencanakan investasi.
- Misalnya, ketika kita berbelanja, kita menggunakan pengurangan untuk menghitung sisa uang yang kita miliki setelah membeli barang.
- Ketika menabung, kita menggunakan penjumlahan untuk mengetahui total tabungan kita setelah beberapa waktu.
- Dalam investasi, kita menggunakan perkalian dan pembagian untuk menghitung keuntungan atau kerugian yang kita peroleh.
Perdagangan
Dalam perdagangan, bilangan aritmatika juga memainkan peran penting. Konsep-konsep seperti persentase, rasio, dan proporsi digunakan untuk menentukan harga jual, menghitung keuntungan, dan menganalisis data penjualan.
- Contohnya, ketika membeli barang dengan diskon, kita menggunakan persentase untuk menghitung harga akhir yang harus kita bayar.
- Pedagang menggunakan rasio dan proporsi untuk menentukan jumlah bahan baku yang dibutuhkan dalam proses produksi.
Ilmu Pengetahuan
Bilangan aritmatika juga berperan penting dalam berbagai bidang ilmu pengetahuan. Dalam fisika, kimia, dan biologi, konsep-konsep matematika dasar digunakan untuk menganalisis data, membangun model, dan memahami fenomena alam.
- Contohnya, dalam fisika, kita menggunakan persamaan matematika untuk menghitung kecepatan, jarak, dan waktu.
- Dalam kimia, kita menggunakan bilangan aritmatika untuk menghitung konsentrasi larutan dan jumlah molekul dalam suatu reaksi.
Contoh Soal
Misalnya, bayangkan Anda ingin membeli sebuah sepeda dengan harga Rp. 2.000.000. Anda memiliki tabungan Rp. 1.500.000. Berapa banyak uang yang harus Anda pinjam untuk membeli sepeda tersebut?
Untuk menyelesaikan masalah ini, kita dapat menggunakan pengurangan. Jumlah uang yang harus Anda pinjam adalah harga sepeda dikurangi tabungan Anda:
Rp. 2.000.000 – Rp. 1.500.000 = Rp. 500.000
Jadi, Anda harus meminjam Rp. 500.000 untuk membeli sepeda tersebut.
Soal Latihan Bilangan Aritmatika
Bilangan aritmetika adalah konsep dasar dalam matematika yang mempelajari tentang urutan bilangan yang memiliki selisih yang sama antar sukunya. Untuk menguji pemahamanmu tentang konsep ini, berikut adalah beberapa soal latihan yang dapat kamu kerjakan.
Soal Latihan Bilangan Aritmetika
Soal-soal latihan berikut ini disusun berdasarkan tingkat kesulitan yang bervariasi, mulai dari yang mudah hingga yang menantang. Selesaikan soal-soal ini dengan cermat dan gunakan rumus-rumus yang telah kamu pelajari untuk membantu kamu menemukan jawaban yang tepat.
| Soal | Langkah Penyelesaian | Jawaban |
|---|---|---|
| Tentukan suku ke-5 dari barisan aritmetika 2, 5, 8, … | Rumus suku ke-n barisan aritmetika: Un = a + (n-1)b Dengan a = 2 (suku pertama), b = 3 (beda), dan n = 5 (suku ke-5) Maka, U5 = 2 + (5-1)3 = 2 + 12 = 14 |
14 |
| Tentukan jumlah 10 suku pertama dari barisan aritmetika 1, 4, 7, … | Rumus jumlah n suku pertama barisan aritmetika: Sn = (n/2)(2a + (n-1)b) Dengan a = 1 (suku pertama), b = 3 (beda), dan n = 10 (jumlah suku) Maka, S10 = (10/2)(2(1) + (10-1)3) = 5(2 + 27) = 145 |
145 |
| Tentukan suku tengah dari barisan aritmetika 3, 7, 11, …, 39 | Rumus suku tengah barisan aritmetika: St = (a + Un)/2 Dengan a = 3 (suku pertama), Un = 39 (suku terakhir) Maka, St = (3 + 39)/2 = 21 |
21 |
| Tentukan nilai x agar barisan 2x, x+3, 2x-1 membentuk barisan aritmetika. | Pada barisan aritmetika, selisih antara dua suku berurutan selalu sama. Maka, (x+3) – 2x = (2x-1) – (x+3) x – 3 = x – 4 -3 = -4 (tidak mungkin) Jadi, tidak ada nilai x yang memenuhi sehingga barisan tersebut membentuk barisan aritmetika. |
Tidak ada nilai x yang memenuhi |
| Sebuah barisan aritmetika memiliki suku pertama 5 dan beda 4. Tentukan jumlah 15 suku pertama dari barisan tersebut. | Rumus jumlah n suku pertama barisan aritmetika: Sn = (n/2)(2a + (n-1)b) Dengan a = 5 (suku pertama), b = 4 (beda), dan n = 15 (jumlah suku) Maka, S15 = (15/2)(2(5) + (15-1)4) = 7.5(10 + 56) = 495 |
495 |
Kesalahan Umum dalam Menyelesaikan Soal Bilangan Aritmatika
Bilangan aritmatika merupakan konsep dasar dalam matematika yang sering dijumpai dalam berbagai bidang kehidupan. Namun, dalam menyelesaikan soal bilangan aritmatika, seringkali terjadi kesalahan yang mengakibatkan jawaban yang salah. Kesalahan ini bisa disebabkan oleh kurangnya pemahaman konsep, kurangnya ketelitian, atau kesalahan dalam penerapan rumus. Memahami kesalahan umum yang sering terjadi dan cara mengatasinya akan membantu kita meningkatkan kemampuan dalam menyelesaikan soal bilangan aritmatika.
Kesalahan dalam Menentukan Operasi Aritmatika
Kesalahan dalam menentukan operasi aritmatika merupakan kesalahan yang umum terjadi dalam menyelesaikan soal bilangan aritmatika. Hal ini dapat disebabkan oleh kurangnya pemahaman terhadap kata kunci dalam soal atau kurangnya ketelitian dalam membaca soal.
- Contohnya, pada soal “Tentukan jumlah dari 5 dan 7”, kesalahan yang sering terjadi adalah siswa melakukan operasi pengurangan atau perkalian, bukan penjumlahan.
- Untuk menghindari kesalahan ini, kita perlu membaca soal dengan teliti dan memahami kata kunci yang menunjukkan operasi aritmatika yang harus dilakukan. Kata kunci seperti “jumlah”, “selisih”, “kali”, dan “bagi” menunjukkan operasi penjumlahan, pengurangan, perkalian, dan pembagian.
Kesalahan dalam Penerapan Rumus
Kesalahan dalam penerapan rumus juga sering terjadi dalam menyelesaikan soal bilangan aritmatika. Hal ini dapat disebabkan oleh kurangnya pemahaman terhadap rumus atau kurangnya ketelitian dalam menuliskan rumus.
- Contohnya, pada soal “Tentukan rata-rata dari 5, 7, dan 9”, kesalahan yang sering terjadi adalah siswa salah menuliskan rumus rata-rata.
- Rumus rata-rata adalah jumlah data dibagi dengan banyaknya data. Kesalahan yang sering terjadi adalah siswa menjumlahkan data tetapi tidak membaginya dengan banyaknya data. Untuk menghindari kesalahan ini, kita perlu memahami rumus dengan benar dan menuliskannya dengan teliti.
Kesalahan dalam Menghitung
Kesalahan dalam menghitung merupakan kesalahan yang sering terjadi dalam menyelesaikan soal bilangan aritmatika. Hal ini dapat disebabkan oleh kurangnya ketelitian dalam melakukan perhitungan atau kurangnya penguasaan konsep dasar matematika.
Contoh soal bilangan aritmatika biasanya berkaitan dengan pola tertentu, seperti mencari suku ke-n atau jumlah beberapa suku. Namun, pola dan perhitungan juga bisa diterapkan dalam konteks yang lebih luas, misalnya dalam contoh soal network planning. Dalam soal tersebut, kita bisa menggunakan konsep deret aritmatika untuk menghitung waktu penyelesaian proyek dengan mempertimbangkan ketergantungan antar tugas.
Sama seperti mencari suku ke-n dalam bilangan aritmatika, kita bisa menghitung waktu penyelesaian akhir proyek dengan memahami urutan tugas dan waktu yang dibutuhkan untuk setiap tugas.
- Contohnya, pada soal “Tentukan hasil dari 12 + 5 x 3”, kesalahan yang sering terjadi adalah siswa melakukan operasi penjumlahan terlebih dahulu, bukan perkalian.
- Dalam operasi aritmatika, perkalian dan pembagian diprioritaskan dibandingkan penjumlahan dan pengurangan. Untuk menghindari kesalahan ini, kita perlu memahami urutan operasi aritmatika dan melakukan perhitungan dengan teliti.
Kesalahan dalam Menginterpretasikan Hasil
Kesalahan dalam menginterpretasikan hasil juga sering terjadi dalam menyelesaikan soal bilangan aritmatika. Hal ini dapat disebabkan oleh kurangnya pemahaman terhadap konteks soal atau kurangnya ketelitian dalam menuliskan jawaban.
- Contohnya, pada soal “Tentukan luas persegi panjang dengan panjang 10 cm dan lebar 5 cm”, kesalahan yang sering terjadi adalah siswa salah menginterpretasikan hasil perhitungan.
- Luas persegi panjang adalah panjang dikalikan lebar. Jika hasil perhitungan adalah 50, maka jawabannya adalah 50 cm², bukan 50 cm. Untuk menghindari kesalahan ini, kita perlu memahami konteks soal dan menuliskan jawaban dengan satuan yang tepat.
Tips dan Trik Menyelesaikan Soal Bilangan Aritmetika
Bilangan aritmetika merupakan konsep dasar dalam matematika yang sering dijumpai dalam berbagai soal, baik di sekolah maupun dalam kehidupan sehari-hari. Untuk menyelesaikan soal-soal bilangan aritmetika dengan cepat dan akurat, ada beberapa tips dan trik yang bisa kamu terapkan. Yuk, simak tips dan triknya berikut ini!
Memahami Konsep Dasar
Sebelum menyelami tips dan trik, pastikan kamu memahami konsep dasar bilangan aritmetika, seperti penjumlahan, pengurangan, perkalian, pembagian, dan operasi lainnya. Pemahaman yang kuat tentang konsep dasar akan memudahkan kamu dalam menyelesaikan soal-soal yang lebih kompleks.
Mengenali Pola dan Rumus
Bilangan aritmetika memiliki pola dan rumus tertentu yang dapat membantu kamu menyelesaikan soal dengan lebih cepat. Misalnya, untuk mencari suku ke-n dalam suatu barisan aritmetika, kamu dapat menggunakan rumus: Un = a + (n-1)d, di mana a adalah suku pertama, d adalah selisih, dan n adalah nomor suku yang ingin dicari.
Membuat Diagram atau Tabel
Membuat diagram atau tabel dapat membantu kamu memvisualisasikan soal dan memudahkan proses penyelesaian. Misalnya, untuk soal yang melibatkan penjumlahan atau pengurangan, kamu dapat membuat tabel untuk mencatat setiap langkah dan hasil yang diperoleh.
Menghindari Kesalahan Umum
Beberapa kesalahan umum yang sering terjadi dalam menyelesaikan soal bilangan aritmetika adalah:
- Kesalahan dalam operasi hitung dasar, seperti penjumlahan, pengurangan, perkalian, dan pembagian.
- Kesalahan dalam memahami tanda operasi, seperti tanda positif dan negatif.
- Kesalahan dalam urutan operasi, seperti operasi perkalian dan pembagian yang harus dikerjakan sebelum penjumlahan dan pengurangan.
Berlatih Secara Rutin
Latihan secara rutin adalah kunci untuk meningkatkan kemampuan dalam menyelesaikan soal bilangan aritmetika. Semakin banyak kamu berlatih, semakin mahir kamu dalam memahami konsep dan mengaplikasikan tips dan trik yang telah dipelajari.
Contoh Penerapan Tips dan Trik, Contoh soal bilangan aritmatika
Misalnya, dalam soal “Tentukan suku ke-10 dari barisan aritmetika 2, 5, 8, 11…”, kamu dapat menggunakan rumus Un = a + (n-1)d. Dalam soal ini, a = 2, d = 3, dan n = 10. Dengan demikian, suku ke-10 adalah: U10 = 2 + (10-1)3 = 2 + 27 = 29.
Kesimpulan
Dengan memahami konsep dasar, mengenali pola dan rumus, membuat diagram atau tabel, menghindari kesalahan umum, dan berlatih secara rutin, kamu dapat menyelesaikan soal-soal bilangan aritmetika dengan lebih cepat dan akurat.
Akhir Kata
Dengan memahami konsep dasar bilangan aritmatika, Anda akan mampu menyelesaikan berbagai masalah matematika dengan lebih mudah dan percaya diri. Tidak hanya dalam pembelajaran, tetapi juga dalam kehidupan sehari-hari, kemampuan menguasai bilangan aritmatika akan sangat membantu Anda dalam mengambil keputusan yang tepat.