Pernahkah Anda membayangkan bahwa rumus matematika yang rumit seperti polinomial ternyata memiliki peran penting dalam kehidupan sehari-hari? Contoh Soal Cerita Polinomial Beserta Jawabannya akan mengajak Anda untuk menjelajahi dunia polinomial dan melihat bagaimana konsep ini diterapkan dalam berbagai situasi, mulai dari menghitung luas dan keliling tanah hingga menganalisis pertumbuhan populasi.
Polinomial adalah ekspresi aljabar yang terdiri dari variabel dan konstanta, yang dihubungkan oleh operasi penjumlahan, pengurangan, dan perkalian. Dalam artikel ini, kita akan mempelajari berbagai jenis polinomial, operasi aljabar yang terkait, dan bagaimana menyelesaikan persamaan polinomial. Selain itu, kita juga akan membahas aplikasi polinomial dalam bidang ekonomi, fisika, teknologi informasi, dan kehidupan sehari-hari.
Pengertian Polinomial
Polinomial merupakan ekspresi aljabar yang terdiri dari variabel dan konstanta, yang dihubungkan oleh operasi penjumlahan, pengurangan, dan perkalian.
Dengan kata lain, polinomial adalah kombinasi dari suku-suku yang melibatkan variabel berpangkat bulat non-negatif.
Contoh Polinomial dalam Kehidupan Sehari-hari
Polinomial sering kali muncul dalam berbagai aspek kehidupan sehari-hari, meskipun kita mungkin tidak menyadarinya. Berikut beberapa contoh:
- Perhitungan luas dan volume: Rumus untuk menghitung luas persegi panjang (panjang x lebar) dan volume kubus (sisi x sisi x sisi) merupakan contoh polinomial sederhana.
- Perhitungan bunga majemuk: Rumus bunga majemuk melibatkan polinomial dengan pangkat yang lebih tinggi.
- Perhitungan lintasan benda: Dalam fisika, polinomial digunakan untuk memodelkan lintasan benda yang bergerak, seperti peluru yang ditembakkan ke udara.
Jenis-Jenis Polinomial Berdasarkan Derajatnya
Derajat polinomial ditentukan oleh pangkat tertinggi dari variabelnya. Berikut tabel yang membandingkan jenis-jenis polinomial berdasarkan derajatnya:
| Derajat | Jenis Polinomial | Contoh |
|---|---|---|
| 0 | Konstanta | 5, -2, 10 |
| 1 | Linear | 2x + 3, -x + 5, 7x |
| 2 | Kuadrat | x^2 + 2x – 1, 3x^2 – 5, 4x^2 |
| 3 | Kubik | x^3 + 2x^2 – x + 4, 2x^3 – 5x, x^3 |
| >3 | Polinomial derajat tinggi | x^4 + 3x^3 – 2x^2 + x – 1, 2x^5 – x^4 + 3x^2 |
Operasi Aljabar pada Polinomial
Polinomial adalah ekspresi aljabar yang terdiri dari variabel dan koefisien, yang dihubungkan dengan operasi penjumlahan, pengurangan, dan perkalian. Operasi aljabar pada polinomial meliputi penjumlahan, pengurangan, perkalian, dan pembagian. Pada bagian ini, kita akan membahas secara rinci operasi-operasi tersebut.
Bingung dengan soal cerita polinomial? Tenang, banyak sumber belajar yang bisa kamu akses! Salah satunya adalah contoh soal cerita polinomial beserta jawabannya yang bisa kamu temukan di berbagai platform online. Nah, buat kamu yang lagi nyiapin diri buat CPNS, kamu bisa juga melatih kemampuan dengan latihan soal-soal CPNS.
Banyak website yang menyediakan contoh soal CPNS dan pembahasan gratis yang bisa kamu manfaatkan untuk belajar. Setelah berlatih dengan soal CPNS, kamu bisa kembali ke soal cerita polinomial dan mencoba mengaplikasikan konsep yang sudah kamu pelajari.
Penjumlahan dan Pengurangan Polinomial
Penjumlahan dan pengurangan polinomial dilakukan dengan menjumlahkan atau mengurangi koefisien suku-suku sejenis. Suku sejenis adalah suku yang memiliki variabel dan pangkat yang sama.
Contoh:
- Tentukan hasil penjumlahan dari polinomial (3x2 + 2x – 1) dan (x2 – 4x + 5).
Penyelesaian:
- (3x2 + 2x – 1) + (x2 – 4x + 5) = (3x2 + x2) + (2x – 4x) + (-1 + 5)
- = 4x2 – 2x + 4
Contoh lain:
- Tentukan hasil pengurangan polinomial (5x3 – 2x2 + 3x) dari (2x3 + 4x2 – 5x).
Penyelesaian:
- (2x3 + 4x2 – 5x) – (5x3 – 2x2 + 3x) = (2x3 – 5x3) + (4x2 + 2x2) + (-5x – 3x)
- = -3x3 + 6x2 – 8x
Perkalian Polinomial
Perkalian polinomial dilakukan dengan mengalikan setiap suku dari polinomial pertama dengan setiap suku dari polinomial kedua. Hasil perkalian kemudian dijumlahkan.
Contoh:
- Tentukan hasil perkalian dari polinomial (2x + 1) dan (x – 3).
Penyelesaian:
- (2x + 1)(x – 3) = 2x(x – 3) + 1(x – 3)
- = 2x2 – 6x + x – 3
- = 2x2 – 5x – 3
Contoh lain:
- Tentukan hasil perkalian dari polinomial (x2 + 2x – 1) dan (3x – 2).
Penyelesaian:
- (x2 + 2x – 1)(3x – 2) = x2(3x – 2) + 2x(3x – 2) – 1(3x – 2)
- = 3x3 – 2x2 + 6x2 – 4x – 3x + 2
- = 3x3 + 4x2 – 7x + 2
Pembagian Polinomial
Pembagian polinomial dapat dilakukan dengan metode panjang atau metode sintetis. Metode panjang mirip dengan pembagian bilangan bulat, sedangkan metode sintetis lebih ringkas. Berikut tabel yang merangkum rumus pembagian polinomial dengan contoh soal:
| Metode | Rumus | Contoh Soal |
|---|---|---|
| Metode Panjang |
Pembagian polinomial dilakukan dengan membagi suku pertama dari polinomial yang dibagi dengan suku pertama dari polinomial pembagi. Hasil bagi dikalikan dengan polinomial pembagi, kemudian dikurangi dari polinomial yang dibagi. Proses ini diulang hingga derajat polinomial sisa lebih rendah dari derajat polinomial pembagi. |
Bagilah polinomial (x3 + 2x2 – 5x + 2) dengan (x – 1). |
| Metode Sintetis |
Metode sintetis menggunakan koefisien dari polinomial yang dibagi dan pembagi. Koefisien polinomial yang dibagi ditulis di baris pertama, dan koefisien pembagi ditulis di kolom pertama. Koefisien pembagi dikalikan dengan koefisien pertama dari polinomial yang dibagi, dan hasilnya ditulis di kolom kedua. Kemudian, hasil kali dijumlahkan dengan koefisien kedua dari polinomial yang dibagi, dan hasilnya ditulis di kolom ketiga. Proses ini diulang hingga semua koefisien dari polinomial yang dibagi telah digunakan. Baris terakhir berisi koefisien dari hasil bagi, dan angka terakhir adalah sisa. |
Bagilah polinomial (x3 + 2x2 – 5x + 2) dengan (x – 1). |
Menyelesaikan Persamaan Polinomial
Persamaan polinomial adalah persamaan yang melibatkan variabel dengan pangkat bulat non-negatif. Penyelesaian persamaan polinomial berarti mencari nilai-nilai variabel yang membuat persamaan tersebut benar. Ada beberapa metode yang dapat digunakan untuk menyelesaikan persamaan polinomial, dan metode yang paling efektif tergantung pada jenis persamaan yang dihadapi.
Metode Penyelesaian Persamaan Polinomial
Beberapa metode yang dapat digunakan untuk menyelesaikan persamaan polinomial antara lain:
- Faktorisasi: Metode ini melibatkan pemfaktoran persamaan polinomial menjadi bentuk perkalian beberapa faktor. Jika suatu faktor sama dengan nol, maka persamaan tersebut akan terpenuhi.
- Rumus Kuadrat: Metode ini digunakan untuk menyelesaikan persamaan kuadrat, yaitu persamaan polinomial dengan derajat dua. Rumus kuadrat memberikan solusi yang tepat untuk persamaan kuadrat.
- Metode Horner: Metode ini merupakan metode numerik yang digunakan untuk mencari akar persamaan polinomial. Metode Horner melibatkan pembagian polinomial dengan faktor linier untuk menemukan akarnya.
- Metode Numerik Lainnya: Terdapat metode numerik lain seperti metode Newton-Raphson dan metode biseksi yang dapat digunakan untuk mencari akar persamaan polinomial.
Penyelesaian Persamaan Polinomial dengan Faktorisasi
Faktorisasi adalah metode yang umum digunakan untuk menyelesaikan persamaan polinomial. Metode ini melibatkan pemfaktoran persamaan polinomial menjadi bentuk perkalian beberapa faktor. Jika suatu faktor sama dengan nol, maka persamaan tersebut akan terpenuhi.
Contoh:
Selesaikan persamaan polinomial berikut:
x² – 5x + 6 = 0
Penyelesaian:
1. Faktorisasi persamaan polinomial:
x² – 5x + 6 = (x – 2)(x – 3) = 0
2. Cari nilai x yang membuat setiap faktor sama dengan nol:
x – 2 = 0 => x = 2
x – 3 = 0 => x = 3
Jadi, solusi dari persamaan polinomial x² – 5x + 6 = 0 adalah x = 2 dan x = 3.
Contoh Soal Penyelesaian Persamaan Polinomial dengan Metode Horner
Metode Horner adalah metode numerik yang digunakan untuk mencari akar persamaan polinomial. Metode ini melibatkan pembagian polinomial dengan faktor linier untuk menemukan akarnya.
Contoh:
Selesaikan persamaan polinomial berikut dengan metode Horner:
x³ – 2x² – 5x + 6 = 0
Penyelesaian:
1. Pilih nilai x yang ingin diuji sebagai akar. Misalnya, kita ingin menguji apakah x = 2 adalah akar persamaan polinomial.
2. Tulis koefisien polinomial dalam bentuk tabel:
| Koefisien | 1 | -2 | -5 | 6 |
|—|—|—|—|—|
| x = 2 | | 2 | 0 | -10 |
|—|—|—|—|—|
| Jumlah | 1 | 0 | -5 | -4 |
3. Turunkan koefisien pertama (1) ke baris jumlah.
4. Kalikan nilai x (2) dengan koefisien pertama (1) dan tulis hasilnya (2) di bawah koefisien kedua (-2).
5. Jumlahkan koefisien kedua (-2) dan hasil perkalian (2) dan tulis hasilnya (0) di baris jumlah.
6. Kalikan nilai x (2) dengan hasil penjumlahan (0) dan tulis hasilnya (0) di bawah koefisien ketiga (-5).
7. Jumlahkan koefisien ketiga (-5) dan hasil perkalian (0) dan tulis hasilnya (-5) di baris jumlah.
8. Kalikan nilai x (2) dengan hasil penjumlahan (-5) dan tulis hasilnya (-10) di bawah koefisien keempat (6).
9. Jumlahkan koefisien keempat (6) dan hasil perkalian (-10) dan tulis hasilnya (-4) di baris jumlah.
Hasil dari pembagian polinomial dengan faktor linier (x – 2) adalah x² – 5. Karena sisa pembagian adalah -4, maka x = 2 bukan akar persamaan polinomial.
Metode Horner dapat digunakan untuk mencari akar persamaan polinomial dengan mengulangi proses ini dengan nilai x yang berbeda.
Penerapan Polinomial dalam Konteks Nyata: Contoh Soal Cerita Polinomial Beserta Jawabannya
Polinomial, dengan sifat-sifat uniknya, ternyata memiliki aplikasi luas di berbagai bidang kehidupan. Dari ekonomi hingga teknologi informasi, polinomial berperan penting dalam memodelkan dan memecahkan berbagai masalah kompleks.
Penerapan Polinomial dalam Ekonomi
Polinomial digunakan dalam ekonomi untuk memodelkan berbagai fenomena ekonomi, seperti hubungan antara permintaan dan penawaran, pertumbuhan ekonomi, dan analisis investasi.
- Fungsi Permintaan dan Penawaran: Polinomial digunakan untuk merepresentasikan hubungan antara harga suatu barang dengan jumlah yang diminta dan ditawarkan. Misalnya, fungsi permintaan linier, yang merupakan polinomial derajat satu, dapat digunakan untuk memodelkan hubungan antara harga dan jumlah barang yang diminta.
- Pertumbuhan Ekonomi: Polinomial dapat digunakan untuk memodelkan pertumbuhan ekonomi jangka pendek dan panjang. Model pertumbuhan ekonomi seringkali menggunakan polinomial untuk merepresentasikan hubungan antara investasi, konsumsi, dan pertumbuhan ekonomi.
- Analisis Investasi: Polinomial digunakan dalam analisis investasi untuk memodelkan aliran kas masa depan dari investasi. Model aliran kas ini dapat digunakan untuk menentukan nilai sekarang bersih (NPV) dari suatu investasi, yang merupakan ukuran keuntungan atau kerugian dari suatu investasi.
Penerapan Polinomial dalam Fisika
Polinomial memiliki peran penting dalam fisika, terutama dalam bidang mekanika, listrik, dan optik.
- Mekanika: Polinomial digunakan untuk memodelkan gerakan benda. Misalnya, persamaan gerak parabola, yang menggambarkan lintasan benda yang dilempar ke atas, merupakan polinomial derajat dua.
- Listrik: Polinomial digunakan untuk memodelkan rangkaian listrik. Misalnya, persamaan tegangan pada resistor, kapasitor, dan induktor, merupakan polinomial derajat satu.
- Optik: Polinomial digunakan untuk memodelkan perilaku cahaya. Misalnya, persamaan lensa tipis, yang menggambarkan bagaimana cahaya dibiaskan oleh lensa, merupakan polinomial derajat dua.
Penerapan Polinomial dalam Teknologi Informasi
Polinomial memiliki aplikasi yang luas dalam teknologi informasi, khususnya dalam bidang pemrosesan sinyal, kriptografi, dan pemodelan data.
- Pemrosesan Sinyal: Polinomial digunakan dalam pemrosesan sinyal untuk merancang filter digital, yang digunakan untuk memisahkan sinyal yang diinginkan dari noise. Misalnya, filter FIR (Finite Impulse Response), yang merupakan filter digital yang umum digunakan, didasarkan pada polinomial.
- Kriptografi: Polinomial digunakan dalam kriptografi untuk membangun algoritma enkripsi dan dekripsi yang aman. Misalnya, algoritma RSA, yang merupakan salah satu algoritma kriptografi yang paling umum digunakan, didasarkan pada polinomial.
- Pemodelan Data: Polinomial digunakan dalam pemodelan data untuk memodelkan hubungan antara variabel. Misalnya, regresi polinomial, yang merupakan teknik statistik untuk memodelkan hubungan non-linier antara variabel, menggunakan polinomial untuk memodelkan hubungan tersebut.
Contoh Soal Cerita Polinomial
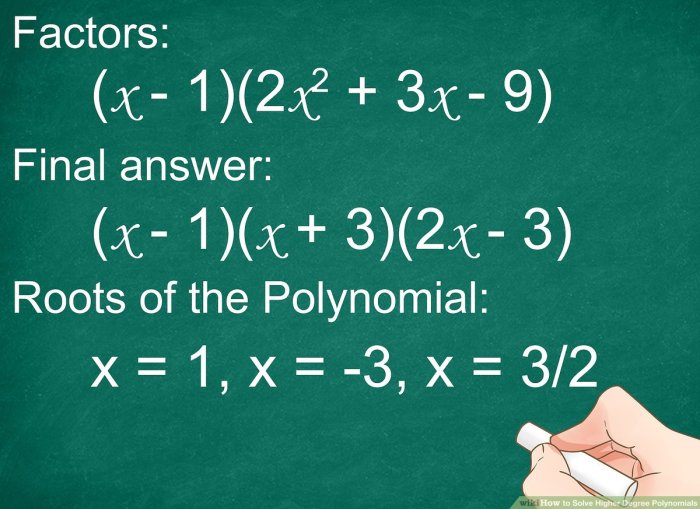
Polinomial adalah ekspresi aljabar yang terdiri dari variabel dan konstanta, dihubungkan dengan operasi penjumlahan, pengurangan, dan perkalian, dengan pangkat variabel yang merupakan bilangan bulat non-negatif. Polinomial seringkali digunakan dalam berbagai bidang, seperti matematika, fisika, dan ekonomi. Untuk memahami aplikasi polinomial, kita dapat menggunakan contoh soal cerita yang menarik dan realistis.
Contoh Soal Cerita Polinomial yang Melibatkan Luas dan Keliling Bangun Datar
Contoh soal cerita polinomial yang melibatkan luas dan keliling bangun datar dapat membantu kita memahami konsep polinomial dalam konteks geometri. Berikut contohnya:
- Sebuah taman berbentuk persegi panjang memiliki panjang (x + 3) meter dan lebar (x – 2) meter. Jika diketahui keliling taman tersebut adalah 26 meter, tentukan luas taman tersebut.
Contoh Soal Cerita Polinomial yang Berkaitan dengan Pertumbuhan Populasi
Pertumbuhan populasi dapat dimodelkan menggunakan polinomial. Berikut contoh soal cerita yang membahas tentang pertumbuhan populasi:
- Populasi suatu kota pada tahun 2020 adalah 10.000 jiwa. Jika pertumbuhan populasi kota tersebut dapat dimodelkan dengan persamaan P(t) = 10.000 + 500t, dengan t adalah waktu dalam tahun, tentukan populasi kota tersebut pada tahun 2025.
Contoh Soal Cerita Polinomial yang Membahas tentang Pembagian Harta Warisan
Pembagian harta warisan dapat diilustrasikan menggunakan polinomial. Berikut contoh soal cerita yang membahas tentang pembagian harta warisan:
- Seorang ayah meninggalkan harta warisan senilai (x^2 + 3x + 2) juta rupiah untuk dibagi kepada ketiga anaknya. Anak pertama mendapat (x + 1) juta rupiah, anak kedua mendapat (x + 2) juta rupiah, dan sisanya untuk anak ketiga. Tentukan berapa juta rupiah yang diterima anak ketiga.
Langkah-langkah Menyelesaikan Soal Cerita Polinomial
Soal cerita polinomial merupakan jenis soal yang menggabungkan konsep matematika polinomial dengan situasi nyata. Soal ini menantang kemampuan kita untuk memahami dan menerjemahkan bahasa sehari-hari ke dalam bahasa matematika. Untuk menyelesaikan soal cerita polinomial, kita perlu memahami langkah-langkah sistematis yang dapat membantu kita dalam mengidentifikasi informasi penting dan merumuskan persamaan yang tepat.
Langkah-langkah Sistematis dalam Menyelesaikan Soal Cerita Polinomial
Berikut adalah langkah-langkah sistematis yang dapat membantu kita dalam menyelesaikan soal cerita polinomial:
- Baca dan Pahami Soal dengan Cermat: Langkah pertama adalah membaca soal cerita dengan teliti dan memahami maksud dari soal tersebut. Pastikan kita memahami setiap kata dan frasa yang digunakan dalam soal.
- Identifikasi Informasi Penting: Setelah memahami soal, kita perlu mengidentifikasi informasi penting yang terdapat dalam soal cerita. Informasi ini biasanya berupa data numerik, variabel, dan hubungan antar variabel.
- Tentukan Variabel: Tentukan variabel yang mewakili besaran yang tidak diketahui dalam soal. Variabel ini biasanya dilambangkan dengan huruf, seperti x, y, atau z.
- Rumuskan Persamaan: Gunakan informasi penting yang telah diidentifikasi untuk merumuskan persamaan matematika yang mewakili situasi dalam soal cerita. Persamaan ini biasanya berupa persamaan polinomial.
- Selesaikan Persamaan: Selesaikan persamaan polinomial yang telah dirumuskan untuk mendapatkan nilai variabel yang tidak diketahui. Kita dapat menggunakan berbagai metode penyelesaian persamaan polinomial, seperti faktorisasi, rumus kuadrat, atau metode numerik.
- Interpretasikan Hasil: Setelah mendapatkan nilai variabel, interpretasikan hasil dalam konteks soal cerita. Pastikan jawaban yang kita peroleh masuk akal dan sesuai dengan situasi dalam soal.
Cara Mengidentifikasi Informasi Penting dalam Soal Cerita Polinomial
Berikut adalah beberapa tips untuk mengidentifikasi informasi penting dalam soal cerita polinomial:
- Perhatikan kata kunci yang menunjukkan operasi matematika, seperti “jumlah”, “selisih”, “kali”, “bagi”, “lebih dari”, “kurang dari”, dan sebagainya.
- Cari hubungan antar variabel yang dijelaskan dalam soal cerita.
- Tentukan besaran yang tidak diketahui dan perlu dicari.
Contoh Langkah-langkah Penyelesaian Soal Cerita Polinomial dengan Diagram
Berikut adalah contoh soal cerita polinomial dan langkah-langkah penyelesaiannya dengan diagram:
Sebuah taman berbentuk persegi panjang memiliki panjang 2 meter lebih panjang dari lebarnya. Luas taman tersebut adalah 15 meter persegi. Tentukan panjang dan lebar taman tersebut.
Berikut adalah langkah-langkah penyelesaian soal cerita polinomial dengan diagram:
- Baca dan Pahami Soal dengan Cermat: Soal cerita menjelaskan tentang sebuah taman berbentuk persegi panjang dengan panjang 2 meter lebih panjang dari lebarnya dan luasnya 15 meter persegi. Kita diminta untuk menentukan panjang dan lebar taman tersebut.
- Identifikasi Informasi Penting: Informasi penting dalam soal cerita ini adalah:
- Panjang taman = Lebar taman + 2 meter
- Luas taman = 15 meter persegi
- Tentukan Variabel: Kita dapat menentukan variabel sebagai berikut:
- Lebar taman = x meter
- Panjang taman = (x + 2) meter
- Rumuskan Persamaan: Kita tahu bahwa luas persegi panjang adalah panjang dikali lebar. Oleh karena itu, kita dapat merumuskan persamaan sebagai berikut:
- Luas taman = Panjang x Lebar
- 15 = (x + 2) x x
- 15 = x² + 2x
- Selesaikan Persamaan: Kita dapat menyelesaikan persamaan kuadrat x² + 2x – 15 = 0 dengan faktorisasi:
- (x + 5)(x – 3) = 0
- x = -5 atau x = 3
Karena lebar tidak mungkin bernilai negatif, maka x = 3.
- Interpretasikan Hasil: Lebar taman adalah 3 meter. Panjang taman adalah x + 2 = 3 + 2 = 5 meter. Jadi, panjang taman adalah 5 meter dan lebar taman adalah 3 meter.
Diagram berikut menunjukkan langkah-langkah penyelesaian soal cerita polinomial:
| Langkah | Keterangan |
| 1 | Membaca dan memahami soal cerita. |
| 2 | Mengidentifikasi informasi penting. |
| 3 | Menentukan variabel. |
| 4 | Merumuskan persamaan. |
| 5 | Menyelesaikan persamaan. |
| 6 | Menerjemahkan hasil. |
Menentukan Rumus Polinomial dari Data
Dalam matematika, polinomial adalah ekspresi aljabar yang terdiri dari variabel dan konstanta, dikombinasikan dengan operasi penjumlahan, pengurangan, dan perkalian. Menentukan rumus polinomial dari data yang diberikan adalah proses penting dalam berbagai bidang, seperti statistik, ilmu komputer, dan teknik.
Interpolasi Polinomial
Interpolasi polinomial adalah metode yang digunakan untuk menentukan rumus polinomial yang melewati semua titik data yang diberikan. Dengan kata lain, polinomial interpolasi akan memberikan nilai yang tepat untuk setiap titik data yang diberikan. Metode ini sangat berguna ketika kita memiliki data yang terbatas dan ingin membuat model matematis yang dapat memprediksi nilai-nilai yang tidak diketahui.
Contoh Data dan Rumus Polinomial
Berikut adalah contoh data dan rumus polinomial yang bersesuaian:
| x | y | Rumus Polinomial |
|---|---|---|
| 0 | 1 | y = 1 |
| 1 | 3 | y = 2x + 1 |
| 2 | 7 | y = 3x^2 – 2x + 1 |
Pada tabel di atas, kita dapat melihat bahwa untuk setiap set data (x, y), terdapat rumus polinomial yang unik yang melewati semua titik data. Rumus polinomial tersebut dapat ditentukan dengan menggunakan berbagai metode interpolasi, seperti metode Lagrange, metode Newton, atau metode Vandermonde.
Metode Interpolasi Polinomial
Metode interpolasi polinomial memungkinkan kita untuk menentukan rumus polinomial yang melewati semua titik data yang diberikan. Ada beberapa metode interpolasi yang tersedia, seperti:
- Metode Lagrange: Metode ini menggunakan polinomial Lagrange untuk menentukan rumus polinomial interpolasi. Polinomial Lagrange adalah polinomial yang memiliki nilai 1 pada satu titik data dan 0 pada semua titik data lainnya.
- Metode Newton: Metode ini menggunakan bentuk polinomial Newton untuk menentukan rumus polinomial interpolasi. Polinomial Newton adalah polinomial yang dibentuk dengan menggunakan selisih terbagi.
- Metode Vandermonde: Metode ini menggunakan matriks Vandermonde untuk menentukan koefisien polinomial interpolasi. Matriks Vandermonde adalah matriks yang berisi pangkat dari titik data.
Setiap metode memiliki kelebihan dan kekurangannya sendiri, dan pilihan metode yang tepat akan bergantung pada data dan kebutuhan yang spesifik.
Grafik Polinomial
Grafik polinomial adalah representasi visual dari persamaan polinomial. Bentuk grafiknya bergantung pada derajat polinomial, koefisiennya, dan konstanta.
Titik Potong Sumbu X dan Y
Titik potong sumbu x adalah titik di mana grafik polinomial memotong sumbu x. Untuk menentukan titik potong sumbu x, kita perlu mencari nilai x ketika y = 0. Titik potong sumbu y adalah titik di mana grafik polinomial memotong sumbu y. Untuk menentukan titik potong sumbu y, kita perlu mencari nilai y ketika x = 0.
Hubungan Koefisien dengan Bentuk Grafik
Koefisien polinomial memiliki pengaruh signifikan terhadap bentuk grafiknya.
- Derajat polinomial: Derajat polinomial menentukan jumlah maksimum titik balik (titik di mana grafik berubah arah). Sebagai contoh, polinomial derajat 2 (kuadrat) memiliki satu titik balik, polinomial derajat 3 (kubik) memiliki dua titik balik, dan seterusnya.
- Koefisien utama: Koefisien utama menentukan arah grafik pada ujung-ujungnya. Jika koefisien utama positif, grafik akan naik ke kanan dan turun ke kiri. Jika koefisien utama negatif, grafik akan turun ke kanan dan naik ke kiri.
- Konstanta: Konstanta menentukan titik potong sumbu y.
Contoh Grafik Polinomial
Berikut adalah beberapa contoh grafik polinomial dengan berbagai derajat:
- Polinomial derajat 1 (linear): Grafiknya adalah garis lurus.
- Polinomial derajat 2 (kuadrat): Grafiknya adalah parabola.
- Polinomial derajat 3 (kubik): Grafiknya memiliki bentuk seperti “S”.
- Polinomial derajat 4 (kuartik): Grafiknya memiliki bentuk seperti “W” atau “M”.
Ilustrasi Grafik
- Polinomial linear (derajat 1): Misalnya, grafik y = 2x + 1 adalah garis lurus dengan kemiringan 2 dan titik potong sumbu y pada (0, 1).
- Polinomial kuadrat (derajat 2): Misalnya, grafik y = x^2 – 2x + 1 adalah parabola yang terbuka ke atas, dengan titik puncak pada (1, 0) dan titik potong sumbu y pada (0, 1).
- Polinomial kubik (derajat 3): Misalnya, grafik y = x^3 – 3x^2 + 2x adalah grafik yang memiliki bentuk seperti “S”, dengan titik potong sumbu x pada (0, 0), (1, 0), dan (2, 0).
- Polinomial kuartik (derajat 4): Misalnya, grafik y = x^4 – 4x^3 + 6x^2 – 4x + 1 adalah grafik yang memiliki bentuk seperti “W”, dengan titik potong sumbu x pada (1, 0) dan titik potong sumbu y pada (0, 1).
Aplikasi Polinomial dalam Komputasi Numerik
Polinomial memiliki peran penting dalam komputasi numerik, khususnya dalam menyelesaikan masalah yang melibatkan fungsi kontinu. Polinomial, dengan sifatnya yang mudah diolah dan dihitung, menjadi alat yang efektif untuk mendekati fungsi kompleks dan menyelesaikan persamaan diferensial, interpolasi, dan integrasi numerik.
Metode Numerik untuk Menyelesaikan Persamaan Diferensial, Contoh soal cerita polinomial beserta jawabannya
Persamaan diferensial merupakan persamaan matematika yang melibatkan turunan fungsi. Metode numerik untuk menyelesaikan persamaan diferensial menggunakan polinomial untuk mendekati solusi fungsi. Salah satu contohnya adalah metode Runge-Kutta. Metode ini menggunakan polinomial untuk mendekati nilai fungsi pada titik-titik tertentu, yang kemudian digunakan untuk menghitung turunan fungsi dan solusi persamaan diferensial.
- Metode Runge-Kutta, khususnya metode Runge-Kutta orde empat, menggunakan polinomial derajat empat untuk mendekati solusi fungsi pada titik-titik tertentu. Metode ini banyak digunakan dalam berbagai aplikasi, seperti simulasi dinamika fluida dan pemodelan sistem fisika.
Interpolasi dan Aproksimasi
Interpolasi adalah proses mencari fungsi yang melewati titik-titik data yang diketahui. Aproksimasi, di sisi lain, adalah proses mencari fungsi yang mendekati data yang diketahui. Polinomial digunakan dalam kedua proses ini karena sifatnya yang mudah dihitung dan fleksibel dalam menyesuaikan dengan data.
- Interpolasi polinomial menggunakan polinomial untuk membangun fungsi yang melewati semua titik data yang diketahui. Contohnya adalah interpolasi Lagrange, yang menggunakan polinomial Lagrange untuk membangun fungsi interpolasi.
- Aproksimasi polinomial menggunakan polinomial untuk mendekati data yang diketahui. Contohnya adalah aproksimasi Taylor, yang menggunakan polinomial Taylor untuk mendekati fungsi di sekitar titik tertentu.
Integrasi Numerik
Integrasi numerik adalah proses menghitung nilai integral fungsi. Polinomial digunakan dalam metode integrasi numerik untuk mendekati fungsi yang diintegralkan.
- Metode Newton-Cotes, seperti aturan trapesium dan aturan Simpson, menggunakan polinomial untuk mendekati fungsi yang diintegralkan. Metode ini mendekati integral dengan menjumlahkan luas daerah di bawah kurva fungsi, yang didekati dengan menggunakan polinomial.
Penutupan
Melalui contoh soal cerita polinomial, kita dapat memahami bahwa matematika bukan hanya sekumpulan rumus yang membingungkan, tetapi alat yang ampuh untuk memecahkan masalah nyata. Dengan memahami konsep polinomial, kita dapat mengaplikasikannya dalam berbagai bidang, meningkatkan kemampuan berpikir logis dan analitis, dan menemukan solusi inovatif untuk berbagai tantangan di sekitar kita.




