Contoh soal dan pembahasan nilai mutlak – Nilai mutlak, konsep matematika yang mungkin terdengar asing bagi sebagian orang, ternyata memiliki peran penting dalam berbagai bidang, mulai dari ilmu pasti hingga kehidupan sehari-hari. Bayangkan, saat kamu mengukur jarak tempuh dari rumah ke sekolah, kamu sebenarnya telah menggunakan konsep nilai mutlak. Nilai mutlak tidak hanya tentang angka, tetapi juga tentang memahami jarak dan selisih.
Dalam artikel ini, kita akan menjelajahi dunia nilai mutlak dengan contoh soal dan pembahasan yang mudah dipahami. Mulai dari pengertian dasar hingga penerapannya dalam berbagai situasi, kita akan mengupas tuntas konsep ini. Siap-siap untuk memahami nilai mutlak dengan lebih dalam!
Pengertian Nilai Mutlak
Nilai mutlak adalah jarak suatu bilangan dari nol pada garis bilangan, tanpa memperhatikan arahnya. Konsep ini sederhana, tetapi penting dalam berbagai bidang matematika, termasuk aljabar, geometri, dan kalkulus.
Contoh Nilai Mutlak dalam Kehidupan Sehari-hari
Misalnya, jika kamu berjalan 5 langkah ke timur dan kemudian 5 langkah ke barat, kamu akan kembali ke titik awal. Jarak total yang kamu tempuh adalah 10 langkah, meskipun posisi akhirmu sama dengan posisi awal. Dalam hal ini, nilai mutlak dari 5 (jarak ke timur) dan -5 (jarak ke barat) sama, yaitu 5.
Tabel Nilai Mutlak
| Bilangan | Nilai Mutlak |
|---|---|
| -5 | 5 |
| -2 | 2 |
| 0 | 0 |
| 3 | 3 |
| 7 | 7 |
| -1/2 | 1/2 |
| 2.5 | 2.5 |
Sifat-Sifat Nilai Mutlak
Nilai mutlak, yang sering dilambangkan dengan tanda garis vertikal (| |), adalah konsep matematika yang merepresentasikan jarak suatu bilangan dari nol pada garis bilangan, tanpa memperhatikan arahnya. Nilai mutlak selalu bernilai positif atau nol. Sifat-sifat nilai mutlak membantu kita memahami dan menyelesaikan berbagai persamaan dan pertidaksamaan yang melibatkan nilai mutlak.
Sifat-Sifat Nilai Mutlak
Berikut ini adalah 5 sifat dasar nilai mutlak yang penting untuk dipahami:
- Sifat 1: Nilai Mutlak Selalu Non-Negatif
Nilai mutlak dari suatu bilangan selalu bernilai positif atau nol. Artinya, untuk setiap bilangan real x, berlaku:
|x| ≥ 0
Contoh: |5| = 5, |-3| = 3, |0| = 0.
- Sifat 2: Nilai Mutlak dari Nol
Nilai mutlak dari nol adalah nol. Artinya, untuk setiap bilangan real x, berlaku:
|0| = 0
Contoh: |0| = 0.
- Sifat 3: Nilai Mutlak dari Bilangan Negatif
Nilai mutlak dari suatu bilangan negatif adalah bilangan positif yang sama dengan besarnya bilangan tersebut. Artinya, untuk setiap bilangan real x, berlaku:
|-x| = x
Contoh: |-5| = 5.
- Sifat 4: Sifat Perkalian
Nilai mutlak dari hasil perkalian dua bilangan sama dengan hasil perkalian nilai mutlak dari kedua bilangan tersebut. Artinya, untuk setiap bilangan real x dan y, berlaku:
|x · y| = |x| · |y|
Contoh: |2 · 3| = |2| · |3| = 6.
- Sifat 5: Sifat Pembagian
Nilai mutlak dari hasil pembagian dua bilangan sama dengan hasil pembagian nilai mutlak dari kedua bilangan tersebut. Artinya, untuk setiap bilangan real x dan y (dengan y ≠ 0), berlaku:
|x / y| = |x| / |y|
Contoh: |6 / 2| = |6| / |2| = 3.
Contoh Soal dan Pembahasan
Berikut ini beberapa contoh soal dan pembahasan yang mengilustrasikan penggunaan sifat-sifat nilai mutlak:
Contoh Soal 1
Hitunglah nilai dari |3 – 5|.
Pembahasan
1. Hitung selisih di dalam tanda nilai mutlak: 3 – 5 = -2.
2. Karena -2 adalah bilangan negatif, maka nilai mutlaknya adalah 2: |-2| = 2.
Contoh soal dan pembahasan nilai mutlak memang penting untuk dipahami, terutama saat mempersiapkan ujian. Nah, buat kamu yang mau latihan soal-soal UN Matematika SMP, kamu bisa cek contoh soal-soal di contoh soal un matematika smp. Soal-soal tersebut bisa membantumu memahami materi dan melatih kemampuan menyelesaikan soal, termasuk soal-soal yang berkaitan dengan nilai mutlak.
Jadi, |3 – 5| = 2.
Contoh Soal 2
Sederhanakan ekspresi |4| · |-2|.
Pembahasan
1. Gunakan sifat perkalian nilai mutlak: |4| · |-2| = |4 · -2|.
2. Hitung perkalian di dalam tanda nilai mutlak: |4 · -2| = |-8|.
3. Nilai mutlak dari -8 adalah 8: |-8| = 8.
Jadi, |4| · |-2| = 8.
Contoh Soal 3
Sederhanakan ekspresi |10 / (-5)|.
Pembahasan
1. Gunakan sifat pembagian nilai mutlak: |10 / (-5)| = |10| / |-5|.
2. Hitung nilai mutlak dari 10 dan -5: |10| = 10, |-5| = 5.
3. Bagi nilai mutlak dari 10 dengan nilai mutlak dari -5: 10 / 5 = 2.
Jadi, |10 / (-5)| = 2.
Tabel Sifat-Sifat Nilai Mutlak
| Sifat | Rumus | Contoh |
|---|---|---|
| Nilai Mutlak Selalu Non-Negatif | |x| ≥ 0 | |5| = 5 |
| Nilai Mutlak dari Nol | |0| = 0 | |0| = 0 |
| Nilai Mutlak dari Bilangan Negatif | |-x| = x | |-3| = 3 |
| Sifat Perkalian | |x · y| = |x| · |y| | |2 · 3| = |2| · |3| = 6 |
| Sifat Pembagian | |x / y| = |x| / |y| | |6 / 2| = |6| / |2| = 3 |
Menyelesaikan Persamaan Nilai Mutlak
Persamaan nilai mutlak adalah persamaan yang memuat tanda nilai mutlak (| |). Menyelesaikan persamaan nilai mutlak berarti mencari nilai variabel yang memenuhi persamaan tersebut. Untuk menyelesaikan persamaan nilai mutlak, kita perlu memahami sifat nilai mutlak dan bagaimana mengaplikasikannya dalam penyelesaian persamaan.
Langkah-langkah Menyelesaikan Persamaan Nilai Mutlak
Untuk menyelesaikan persamaan nilai mutlak, kita dapat mengikuti langkah-langkah berikut:
- Tentukan nilai mutlak dari variabel. Nilai mutlak suatu variabel adalah jaraknya dari nol pada garis bilangan. Misalnya, |2| = 2 dan |-2| = 2.
- Selesaikan persamaan untuk kedua kemungkinan nilai variabel. Karena nilai mutlak dapat positif atau negatif, kita perlu menyelesaikan persamaan untuk kedua kemungkinan tersebut. Misalnya, jika |x| = 3, maka x = 3 atau x = -3.
- Verifikasi solusi. Setelah mendapatkan solusi, kita perlu menguji apakah solusi tersebut memenuhi persamaan asli. Solusi yang tidak memenuhi persamaan asli disebut solusi asing.
Contoh Soal dan Pembahasan
Berikut adalah contoh soal dan pembahasan langkah demi langkah untuk menyelesaikan persamaan nilai mutlak:
Soal:
Selesaikan persamaan nilai mutlak |2x – 1| = 5.
Pembahasan:
- Tentukan nilai mutlak dari variabel. |2x – 1| = 5, artinya 2x – 1 = 5 atau 2x – 1 = -5.
- Selesaikan persamaan untuk kedua kemungkinan nilai variabel.
- Untuk 2x – 1 = 5, maka 2x = 6 dan x = 3.
- Untuk 2x – 1 = -5, maka 2x = -4 dan x = -2.
- Verifikasi solusi.
- Untuk x = 3, |2(3) – 1| = |5| = 5, sehingga x = 3 memenuhi persamaan.
- Untuk x = -2, |2(-2) – 1| = |-5| = 5, sehingga x = -2 memenuhi persamaan.
Jadi, solusi persamaan |2x – 1| = 5 adalah x = 3 atau x = -2.
Persamaan Nilai Mutlak dengan 2 Variabel, Contoh soal dan pembahasan nilai mutlak
Persamaan nilai mutlak dengan 2 variabel dapat diselesaikan dengan menggunakan metode substitusi atau eliminasi. Berikut adalah contoh soal dan langkah penyelesaiannya:
Soal:
Selesaikan sistem persamaan nilai mutlak berikut:
- |x + y| = 3
- |x – y| = 1
Pembahasan:
- Tentukan nilai mutlak dari variabel.
- Untuk |x + y| = 3, maka x + y = 3 atau x + y = -3.
- Untuk |x – y| = 1, maka x – y = 1 atau x – y = -1.
- Selesaikan sistem persamaan untuk keempat kemungkinan nilai variabel.
- Untuk x + y = 3 dan x – y = 1, maka dengan eliminasi y, kita peroleh 2x = 4 dan x = 2. Substitusikan x = 2 ke salah satu persamaan, misal x + y = 3, maka y = 1.
- Untuk x + y = 3 dan x – y = -1, maka dengan eliminasi y, kita peroleh 2x = 2 dan x = 1. Substitusikan x = 1 ke salah satu persamaan, misal x + y = 3, maka y = 2.
- Untuk x + y = -3 dan x – y = 1, maka dengan eliminasi y, kita peroleh 2x = -2 dan x = -1. Substitusikan x = -1 ke salah satu persamaan, misal x + y = -3, maka y = -2.
- Untuk x + y = -3 dan x – y = -1, maka dengan eliminasi y, kita peroleh 2x = -4 dan x = -2. Substitusikan x = -2 ke salah satu persamaan, misal x + y = -3, maka y = -1.
- Verifikasi solusi.
- Untuk x = 2 dan y = 1, |2 + 1| = 3 dan |2 – 1| = 1, sehingga solusi ini memenuhi persamaan.
- Untuk x = 1 dan y = 2, |1 + 2| = 3 dan |1 – 2| = 1, sehingga solusi ini memenuhi persamaan.
- Untuk x = -1 dan y = -2, |-1 – 2| = 3 dan |-1 + 2| = 1, sehingga solusi ini memenuhi persamaan.
- Untuk x = -2 dan y = -1, |-2 – 1| = 3 dan |-2 + 1| = 1, sehingga solusi ini memenuhi persamaan.
Jadi, solusi sistem persamaan nilai mutlak |x + y| = 3 dan |x – y| = 1 adalah (x, y) = (2, 1), (1, 2), (-1, -2), dan (-2, -1).
Menyelesaikan Pertidaksamaan Nilai Mutlak
Pertidaksamaan nilai mutlak adalah pertidaksamaan yang melibatkan ekspresi nilai mutlak. Memecahkan pertidaksamaan ini melibatkan memahami sifat nilai mutlak dan menggunakan teknik aljabar untuk mengisolasi variabel.
Langkah-langkah Menyelesaikan Pertidaksamaan Nilai Mutlak
Berikut adalah langkah-langkah umum untuk menyelesaikan pertidaksamaan nilai mutlak:
- Identifikasi bentuk pertidaksamaan: Tentukan apakah pertidaksamaan tersebut dalam bentuk $|x| a$, $|x| \leq a$, atau $|x| \geq a$.
- Pisahkan menjadi dua kasus: Untuk pertidaksamaan bentuk $|x| < a$ atau $|x| \leq a$, kita perlu memecahkan dua kasus:
- Kasus 1: $x < a$
- Kasus 2: $x > -a$
Untuk pertidaksamaan bentuk $|x| > a$ atau $|x| \geq a$, kita perlu memecahkan dua kasus:
- Kasus 1: $x > a$
- Kasus 2: $x < -a$
- Selesaikan setiap kasus: Selesaikan pertidaksamaan dalam setiap kasus secara terpisah.
- Gabungkan solusi: Gabungkan solusi dari kedua kasus untuk mendapatkan solusi keseluruhan pertidaksamaan nilai mutlak.
Contoh Soal dan Pembahasan
Berikut adalah contoh soal dan pembahasan langkah demi langkah untuk menyelesaikan pertidaksamaan nilai mutlak:
Contoh 1: $|x – 2| < 5$
Langkah 1: Identifikasi bentuk pertidaksamaan
Pertidaksamaan ini dalam bentuk $|x| < a$.
Langkah 2: Pisahkan menjadi dua kasus
- Kasus 1: $x – 2 < 5$
- Kasus 2: $x – 2 > -5$
Langkah 3: Selesaikan setiap kasus
- Kasus 1: $x – 2 < 5 \Rightarrow x < 7$
- Kasus 2: $x – 2 > -5 \Rightarrow x > -3$
Langkah 4: Gabungkan solusi
Solusi keseluruhan adalah $-3 < x < 7$.
Contoh 2: $|2x + 1| \geq 3$
Langkah 1: Identifikasi bentuk pertidaksamaan
Pertidaksamaan ini dalam bentuk $|x| \geq a$.
Langkah 2: Pisahkan menjadi dua kasus
- Kasus 1: $2x + 1 \geq 3$
- Kasus 2: $2x + 1 \leq -3$
Langkah 3: Selesaikan setiap kasus
- Kasus 1: $2x + 1 \geq 3 \Rightarrow 2x \geq 2 \Rightarrow x \geq 1$
- Kasus 2: $2x + 1 \leq -3 \Rightarrow 2x \leq -4 \Rightarrow x \leq -2$
Langkah 4: Gabungkan solusi
Solusi keseluruhan adalah $x \leq -2$ atau $x \geq 1$.
Tabel Solusi Pertidaksamaan Nilai Mutlak
| Bentuk Pertidaksamaan | Solusi |
|---|---|
| $|x| < a$ | $-a < x < a$ |
| $|x| \leq a$ | $-a \leq x \leq a$ |
| $|x| > a$ | $x a$ |
| $|x| \geq a$ | $x \leq -a$ atau $x \geq a$ |
Penerapan Nilai Mutlak dalam Kehidupan Sehari-hari
Nilai mutlak merupakan konsep matematika yang memiliki peran penting dalam berbagai bidang, termasuk matematika, fisika, dan ekonomi. Dalam kehidupan sehari-hari, nilai mutlak membantu kita memahami jarak, selisih, dan besaran tanpa mempertimbangkan arah.
Penerapan Nilai Mutlak dalam Matematika
Nilai mutlak dalam matematika sering digunakan untuk menghitung jarak antara dua titik pada garis bilangan. Misalnya, jarak antara titik -3 dan 3 pada garis bilangan adalah 6, yang dapat dihitung dengan menggunakan nilai mutlak: |3 – (-3)| = |6| = 6. Selain itu, nilai mutlak juga digunakan dalam persamaan dan pertidaksamaan untuk menentukan solusi yang memenuhi persyaratan tertentu.
Penerapan Nilai Mutlak dalam Fisika
Dalam fisika, nilai mutlak sering digunakan untuk menghitung besarnya besaran fisika, seperti kecepatan, percepatan, dan gaya. Kecepatan adalah besaran skalar yang hanya memiliki nilai, tidak memiliki arah. Misalnya, jika sebuah mobil bergerak dengan kecepatan 20 m/s ke arah timur, maka kecepatannya adalah 20 m/s, tanpa mempertimbangkan arah. Nilai mutlak juga digunakan dalam menghitung gaya, yang merupakan besaran vektor yang memiliki nilai dan arah. Misalnya, gaya gravitasi bumi pada benda memiliki nilai dan arah tertentu.
Penerapan Nilai Mutlak dalam Ekonomi
Dalam ekonomi, nilai mutlak digunakan untuk menghitung selisih antara nilai yang diharapkan dan nilai yang sebenarnya. Misalnya, dalam analisis keuangan, nilai mutlak dapat digunakan untuk menghitung selisih antara keuntungan yang diharapkan dan keuntungan yang sebenarnya. Selain itu, nilai mutlak juga digunakan dalam analisis statistik untuk menghitung deviasi standar, yang mengukur penyebaran data di sekitar nilai rata-rata.
Contoh Ilustrasi Penerapan Nilai Mutlak
Bayangkan sebuah peta dengan kota A dan kota B. Anda ingin mengetahui jarak antara kedua kota tersebut. Anda dapat menggunakan nilai mutlak untuk menghitung jarak tersebut. Misalnya, jika kota A terletak pada koordinat (2, 3) dan kota B terletak pada koordinat (5, 7), maka jarak antara kedua kota tersebut adalah:
|5 – 2| + |7 – 3| = |3| + |4| = 3 + 4 = 7
Jadi, jarak antara kota A dan kota B adalah 7 satuan.
Soal Latihan dan Pembahasan Nilai Mutlak
Nilai mutlak merupakan konsep penting dalam matematika yang digunakan untuk menyatakan jarak suatu bilangan dari nol. Untuk menguasai konsep nilai mutlak, latihan soal dan pembahasannya sangatlah penting. Berikut ini beberapa contoh soal latihan dan pembahasannya.
Soal Latihan Nilai Mutlak
Berikut ini lima soal latihan tentang nilai mutlak dengan tingkat kesulitan yang berbeda.
- Tentukan nilai dari | -5 |.
- Selesaikan persamaan | x – 3 | = 5.
- Tentukan himpunan penyelesaian dari pertidaksamaan | 2x + 1 | < 7.
- Hitung nilai dari | 3x – 2 | + | x + 1 | jika x = -2.
- Tentukan nilai x yang memenuhi pertidaksamaan | x – 1 | > | 2x + 3 |.
Pembahasan Soal Latihan Nilai Mutlak
Berikut ini pembahasan lengkap untuk setiap soal latihan yang telah disusun.
| No. | Soal | Pembahasan |
|---|---|---|
| 1 | Tentukan nilai dari | -5 |. | Nilai mutlak dari -5 adalah jarak antara -5 dan 0 pada garis bilangan, yaitu 5. Jadi, | -5 | = 5. |
| 2 | Selesaikan persamaan | x – 3 | = 5. | Persamaan | x – 3 | = 5 memiliki dua kemungkinan solusi: * x – 3 = 5, sehingga x = 8. * x – 3 = -5, sehingga x = -2. Jadi, himpunan penyelesaian dari persamaan | x – 3 | = 5 adalah -2, 8 . |
| 3 | Tentukan himpunan penyelesaian dari pertidaksamaan | 2x + 1 | < 7. | Pertidaksamaan | 2x + 1 | < 7 memiliki dua kemungkinan: * 2x + 1 < 7, sehingga 2x < 6 dan x < 3. * 2x + 1 > -7, sehingga 2x > -8 dan x > -4. Jadi, himpunan penyelesaian dari pertidaksamaan | 2x + 1 | < 7 adalah x | -4 < x < 3 . |
| 4 | Hitung nilai dari | 3x – 2 | + | x + 1 | jika x = -2. | Jika x = -2, maka: * | 3x – 2 | = | 3(-2) – 2 | = | -8 | = 8. * | x + 1 | = | -2 + 1 | = | -1 | = 1. Jadi, | 3x – 2 | + | x + 1 | = 8 + 1 = 9. |
| 5 | Tentukan nilai x yang memenuhi pertidaksamaan | x – 1 | > | 2x + 3 |. | Pertidaksamaan | x – 1 | > | 2x + 3 | memiliki dua kemungkinan: * x – 1 > 2x + 3, sehingga -x > 4 dan x < -4. * x – 1 < – (2x + 3), sehingga 3x < -2 dan x < -2/3. Jadi, himpunan penyelesaian dari pertidaksamaan | x – 1 | > | 2x + 3 | adalah x | x < -4 . |
Kumpulan Rumus Nilai Mutlak
Nilai mutlak merupakan konsep penting dalam matematika yang sering muncul dalam berbagai bidang, seperti aljabar, geometri, dan kalkulus. Nilai mutlak dari suatu bilangan adalah jarak bilangan tersebut dari nol pada garis bilangan, tanpa mempertimbangkan arah.
Definisi Nilai Mutlak
Definisi nilai mutlak dari suatu bilangan real *x*, dilambangkan dengan |*x*|, adalah sebagai berikut:
|*x*| = *x*, jika *x* ≥ 0
|*x*| = -*x*, jika *x* < 0
Contoh:
* |3| = 3, karena 3 ≥ 0
* |-5| = 5, karena -5 < 0
Sifat-Sifat Nilai Mutlak
Nilai mutlak memiliki beberapa sifat penting yang dapat membantu kita dalam menyelesaikan masalah yang melibatkan nilai mutlak. Berikut adalah beberapa sifatnya:
- |*x*| ≥ 0 untuk setiap bilangan real *x*.
- |*x*| = 0 jika dan hanya jika *x* = 0.
- |- *x*| = |*x*| untuk setiap bilangan real *x*.
- |*x* * y*| = |*x*| * |*y*| untuk setiap bilangan real *x* dan *y*.
- |*x* / *y*| = |*x*| / |*y*| untuk setiap bilangan real *x* dan *y* dengan *y* ≠ 0.
- |*x* + *y*| ≤ |*x*| + |*y*| (Ketidaksamaan Segitiga)
Persamaan Nilai Mutlak
Persamaan nilai mutlak adalah persamaan yang memuat nilai mutlak. Untuk menyelesaikan persamaan nilai mutlak, kita dapat menggunakan definisi nilai mutlak dan sifat-sifatnya.
Contoh Soal dan Pembahasan
Berikut adalah beberapa contoh soal dan pembahasan yang melibatkan persamaan nilai mutlak:
-
Tentukan himpunan penyelesaian dari persamaan |*x* – 2| = 5.
Penyelesaian:
Kita dapat menyelesaikan persamaan ini dengan menggunakan definisi nilai mutlak. Kita tahu bahwa |*x* – 2| = 5 jika dan hanya jika *x* – 2 = 5 atau *x* – 2 = -5. Kita selesaikan kedua persamaan ini:
- *x* – 2 = 5 ⇒ *x* = 7
- *x* – 2 = -5 ⇒ *x* = -3
Jadi, himpunan penyelesaian dari persamaan |*x* – 2| = 5 adalah -3, 7 .
-
Tentukan himpunan penyelesaian dari persamaan |2*x* + 1| = |*x* – 3|.
Penyelesaian:
Kita dapat menyelesaikan persamaan ini dengan menggunakan definisi nilai mutlak dan sifat-sifatnya. Kita tahu bahwa |2*x* + 1| = |*x* – 3| jika dan hanya jika 2*x* + 1 = *x* – 3 atau 2*x* + 1 = -(*x* – 3). Kita selesaikan kedua persamaan ini:
- 2*x* + 1 = *x* – 3 ⇒ *x* = -4
- 2*x* + 1 = -(*x* – 3) ⇒ 3*x* = 2 ⇒ *x* = 2/3
Jadi, himpunan penyelesaian dari persamaan |2*x* + 1| = |*x* – 3| adalah -4, 2/3 .
Pertidaksamaan Nilai Mutlak
Pertidaksamaan nilai mutlak adalah pertidaksamaan yang memuat nilai mutlak. Untuk menyelesaikan pertidaksamaan nilai mutlak, kita dapat menggunakan definisi nilai mutlak dan sifat-sifatnya.
Contoh Soal dan Pembahasan
Berikut adalah beberapa contoh soal dan pembahasan yang melibatkan pertidaksamaan nilai mutlak:
-
Tentukan himpunan penyelesaian dari pertidaksamaan |*x* – 3| < 2.
Penyelesaian:
Kita dapat menyelesaikan pertidaksamaan ini dengan menggunakan definisi nilai mutlak. Kita tahu bahwa |*x* – 3| < 2 jika dan hanya jika -2 < *x* – 3 < 2. Kita selesaikan pertidaksamaan ini:
- -2 1
- *x* – 3 < 2 ⇒ *x* < 5
Jadi, himpunan penyelesaian dari pertidaksamaan |*x* – 3| < 2 adalah *x* | 1 < *x* < 5 .
-
Tentukan himpunan penyelesaian dari pertidaksamaan |2*x* + 1| ≥ 5.
Penyelesaian:
Kita dapat menyelesaikan pertidaksamaan ini dengan menggunakan definisi nilai mutlak. Kita tahu bahwa |2*x* + 1| ≥ 5 jika dan hanya jika 2*x* + 1 ≥ 5 atau 2*x* + 1 ≤ -5. Kita selesaikan kedua pertidaksamaan ini:
- 2*x* + 1 ≥ 5 ⇒ *x* ≥ 2
- 2*x* + 1 ≤ -5 ⇒ *x* ≤ -3
Jadi, himpunan penyelesaian dari pertidaksamaan |2*x* + 1| ≥ 5 adalah *x* | *x* ≤ -3 atau *x* ≥ 2 .
Tabel Rumus Nilai Mutlak
Berikut adalah tabel yang merangkum rumus-rumus nilai mutlak dan contohnya:
| Rumus | Contoh |
|---|---|
| |*x*| = *x*, jika *x* ≥ 0 | |3| = 3 |
| |*x*| = -*x*, jika *x* < 0 | |-5| = 5 |
| |*x*| ≥ 0 untuk setiap bilangan real *x* | |2| ≥ 0 |
| |*x*| = 0 jika dan hanya jika *x* = 0 | |0| = 0 |
| |- *x*| = |*x*| untuk setiap bilangan real *x* | |-3| = |3| |
| |*x* * y*| = |*x*| * |*y*| untuk setiap bilangan real *x* dan *y* | |2 * 3| = |2| * |3| |
| |*x* / *y*| = |*x*| / |*y*| untuk setiap bilangan real *x* dan *y* dengan *y* ≠ 0 | |6 / 2| = |6| / |2| |
| |*x* + *y*| ≤ |*x*| + |*y*| (Ketidaksamaan Segitiga) | |2 + 3| ≤ |2| + |3| |
Tips dan Trik Mengerjakan Soal Nilai Mutlak
Nilai mutlak merupakan konsep penting dalam matematika yang sering muncul dalam berbagai soal. Memahami sifat dan cara menghitung nilai mutlak sangat penting untuk menyelesaikan soal-soal dengan mudah dan cepat. Berikut beberapa tips dan trik yang bisa kamu gunakan untuk menaklukkan soal nilai mutlak:
Memahami Konsep Dasar Nilai Mutlak
Nilai mutlak dari suatu bilangan adalah jarak bilangan tersebut dari nol pada garis bilangan. Artinya, nilai mutlak selalu bernilai positif atau nol. Simbol nilai mutlak adalah garis vertikal di sekitar bilangan, seperti |x|. Contohnya, |3| = 3 dan |-3| = 3.
Menggunakan Definisi Nilai Mutlak
Definisi nilai mutlak dapat digunakan untuk menyelesaikan soal-soal yang melibatkan persamaan atau pertidaksamaan nilai mutlak. Definisi nilai mutlak menyatakan bahwa:
|x| = x jika x ≥ 0
|x| = -x jika x < 0
Contohnya, untuk menyelesaikan persamaan |x – 2| = 5, kita dapat menggunakan definisi nilai mutlak:
- Jika x – 2 ≥ 0, maka |x – 2| = x – 2, sehingga x – 2 = 5 dan x = 7.
- Jika x – 2 < 0, maka |x – 2| = -(x – 2), sehingga -(x – 2) = 5 dan x = -3.
Jadi, solusi persamaan |x – 2| = 5 adalah x = 7 atau x = -3.
Menggunakan Sifat Nilai Mutlak
Ada beberapa sifat nilai mutlak yang dapat membantu dalam menyelesaikan soal-soal nilai mutlak:
- |x| ≥ 0 untuk semua nilai x.
- |x| = |-x| untuk semua nilai x.
- |x|² = x² untuk semua nilai x.
- |x * y| = |x| * |y| untuk semua nilai x dan y.
- |x / y| = |x| / |y| untuk semua nilai x dan y, dengan y ≠ 0.
Sifat-sifat ini dapat digunakan untuk menyederhanakan persamaan atau pertidaksamaan nilai mutlak, sehingga lebih mudah diselesaikan.
Menghilangkan Nilai Mutlak dengan Kuadrat
Salah satu cara untuk menghilangkan nilai mutlak adalah dengan mengkuadratkan kedua ruas persamaan atau pertidaksamaan. Misalnya, untuk menyelesaikan persamaan |x – 2| = 3, kita dapat mengkuadratkan kedua ruas:
|x – 2|² = 3²
Ini menghasilkan persamaan (x – 2)² = 9. Selanjutnya, kita dapat menyelesaikan persamaan kuadrat ini untuk mendapatkan nilai x.
Menggunakan Grafik untuk Visualisasi
Grafik dapat membantu kita untuk memvisualisasikan solusi dari persamaan atau pertidaksamaan nilai mutlak. Misalnya, untuk menyelesaikan pertidaksamaan |x – 2| < 3, kita dapat menggambar grafik fungsi y = |x – 2| dan y = 3. Solusi dari pertidaksamaan ini adalah nilai x yang membuat grafik y = |x – 2| berada di bawah grafik y = 3.
Memperhatikan Kondisi Batas
Saat menyelesaikan soal nilai mutlak, penting untuk memperhatikan kondisi batas yang terkait dengan definisi nilai mutlak. Kondisi batas ini dapat membantu kita menentukan interval nilai x yang memenuhi persamaan atau pertidaksamaan.
Berlatih dengan Soal-Soal
Cara terbaik untuk menguasai soal nilai mutlak adalah dengan berlatih secara rutin. Semakin banyak soal yang kamu kerjakan, semakin mudah kamu memahami konsep dan strategi untuk menyelesaikan soal-soal nilai mutlak.
Contoh Soal dan Pembahasan Nilai Mutlak Tingkat Lanjut
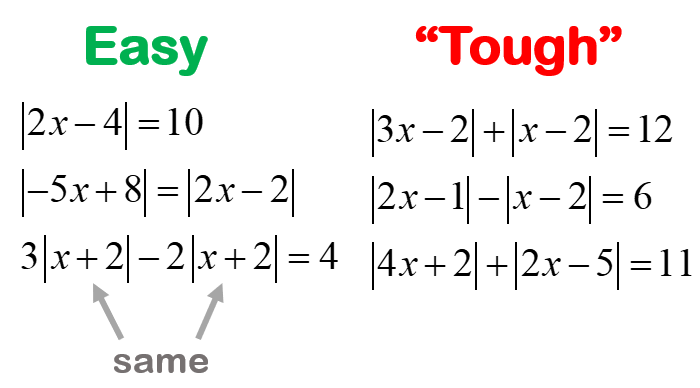
Setelah memahami konsep dasar nilai mutlak, kita akan melangkah ke contoh soal yang lebih menantang. Soal-soal ini memerlukan pemahaman yang lebih mendalam tentang sifat-sifat nilai mutlak dan bagaimana mengaplikasikannya dalam berbagai situasi. Mari kita bahas beberapa contoh soal berikut:
Contoh Soal 1: Persamaan Nilai Mutlak dengan Variabel di Dalam dan Luar
Selesaikan persamaan nilai mutlak berikut:
|2x – 3| + |x + 1| = 5
Pembahasan:
Untuk menyelesaikan persamaan nilai mutlak ini, kita perlu memisahkan persamaan menjadi beberapa kasus berdasarkan tanda dari ekspresi di dalam tanda mutlak.
- Kasus 1: 2x – 3 ≥ 0 dan x + 1 ≥ 0. Artinya, x ≥ 3/2 dan x ≥ -1. Irisan dari kedua kondisi ini adalah x ≥ 3/2.
- Kasus 2: 2x – 3 ≥ 0 dan x + 1 < 0. Artinya, x ≥ 3/2 dan x < -1. Tidak ada irisan dari kedua kondisi ini.
- Kasus 3: 2x – 3 < 0 dan x + 1 ≥ 0. Artinya, x < 3/2 dan x ≥ -1. Irisan dari kedua kondisi ini adalah -1 ≤ x < 3/2.
- Kasus 4: 2x – 3 < 0 dan x + 1 < 0. Artinya, x < 3/2 dan x < -1. Irisan dari kedua kondisi ini adalah x < -1.
Sekarang, kita selesaikan persamaan untuk setiap kasus:
- Kasus 1 (x ≥ 3/2): (2x – 3) + (x + 1) = 5. Selesaikan persamaan ini, kita dapatkan x = 7/3.
- Kasus 3 (-1 ≤ x < 3/2): (3 – 2x) + (x + 1) = 5. Selesaikan persamaan ini, kita dapatkan x = -1.
- Kasus 4 (x < -1): (3 – 2x) + (-x – 1) = 5. Selesaikan persamaan ini, kita dapatkan x = -1.
Jadi, solusi dari persamaan |2x – 3| + |x + 1| = 5 adalah x = 7/3 dan x = -1.
Contoh Soal 2: Pertidaksamaan Nilai Mutlak dengan Variabel di Dalam dan Luar
Tentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak berikut:
|x – 2| + |x + 3| < 7
Pembahasan:
Mirip dengan contoh soal sebelumnya, kita perlu memisahkan pertidaksamaan menjadi beberapa kasus berdasarkan tanda dari ekspresi di dalam tanda mutlak.
- Kasus 1: x – 2 ≥ 0 dan x + 3 ≥ 0. Artinya, x ≥ 2 dan x ≥ -3. Irisan dari kedua kondisi ini adalah x ≥ 2.
- Kasus 2: x – 2 ≥ 0 dan x + 3 < 0. Artinya, x ≥ 2 dan x < -3. Tidak ada irisan dari kedua kondisi ini.
- Kasus 3: x – 2 < 0 dan x + 3 ≥ 0. Artinya, x < 2 dan x ≥ -3. Irisan dari kedua kondisi ini adalah -3 ≤ x < 2.
- Kasus 4: x – 2 < 0 dan x + 3 < 0. Artinya, x < 2 dan x < -3. Irisan dari kedua kondisi ini adalah x < -3.
Sekarang, kita selesaikan pertidaksamaan untuk setiap kasus:
- Kasus 1 (x ≥ 2): (x – 2) + (x + 3) < 7. Selesaikan pertidaksamaan ini, kita dapatkan x < 3. Irisan dari x ≥ 2 dan x < 3 adalah 2 ≤ x < 3.
- Kasus 3 (-3 ≤ x < 2): (2 – x) + (x + 3) < 7. Selesaikan pertidaksamaan ini, kita dapatkan x < 2. Irisan dari -3 ≤ x < 2 dan x < 2 adalah -3 ≤ x < 2.
- Kasus 4 (x < -3): (2 – x) + (-x – 3) -4. Irisan dari x -4 adalah -4 < x < -3.
Jadi, himpunan penyelesaian dari pertidaksamaan |x – 2| + |x + 3| < 7 adalah -4 < x < 3.
Contoh Soal 3: Nilai Mutlak dalam Persamaan Kuadrat
Tentukan himpunan penyelesaian dari persamaan kuadrat berikut:
|x² – 4| = x + 2
Pembahasan:
Persamaan ini melibatkan nilai mutlak dari ekspresi kuadrat. Kita perlu memisahkan persamaan menjadi dua kasus berdasarkan tanda dari ekspresi di dalam tanda mutlak.
- Kasus 1: x² – 4 ≥ 0. Artinya, x ≤ -2 atau x ≥ 2.
- Kasus 2: x² – 4 < 0. Artinya, -2 < x < 2.
Sekarang, kita selesaikan persamaan untuk setiap kasus:
- Kasus 1 (x ≤ -2 atau x ≥ 2): x² – 4 = x + 2. Selesaikan persamaan kuadrat ini, kita dapatkan x = -1 atau x = 3. Namun, hanya x = 3 yang memenuhi kondisi x ≤ -2 atau x ≥ 2.
- Kasus 2 (-2 < x < 2): 4 – x² = x + 2. Selesaikan persamaan kuadrat ini, kita dapatkan x = -2 atau x = 1. Namun, hanya x = 1 yang memenuhi kondisi -2 < x < 2.
Jadi, himpunan penyelesaian dari persamaan |x² – 4| = x + 2 adalah x = 1 dan x = 3.
Tabel Rangkuman Soal dan Pembahasan
| No | Soal | Pembahasan |
|---|---|---|
| 1 | |2x – 3| + |x + 1| = 5 | Memisahkan persamaan menjadi beberapa kasus berdasarkan tanda dari ekspresi di dalam tanda mutlak. Selesaikan persamaan untuk setiap kasus dan gabungkan solusi yang memenuhi semua kondisi. |
| 2 | |x – 2| + |x + 3| < 7 | Memisahkan pertidaksamaan menjadi beberapa kasus berdasarkan tanda dari ekspresi di dalam tanda mutlak. Selesaikan pertidaksamaan untuk setiap kasus dan gabungkan solusi yang memenuhi semua kondisi. |
| 3 | |x² – 4| = x + 2 | Memisahkan persamaan menjadi dua kasus berdasarkan tanda dari ekspresi di dalam tanda mutlak. Selesaikan persamaan kuadrat untuk setiap kasus dan verifikasi solusi yang memenuhi kondisi awal. |
Referensi dan Sumber Belajar Nilai Mutlak: Contoh Soal Dan Pembahasan Nilai Mutlak
Mencari sumber belajar yang tepat untuk memahami konsep nilai mutlak bisa menjadi tantangan. Ada banyak buku, artikel, dan website yang membahas topik ini, namun tidak semuanya mudah dipahami atau akurat. Untuk membantu Anda, berikut ini beberapa rekomendasi sumber belajar yang terpercaya dan mudah dipahami.
Rekomendasi Buku
Buku teks matematika tingkat sekolah menengah pertama dan atas biasanya membahas konsep nilai mutlak dengan cukup detail. Berikut beberapa buku yang bisa Anda jadikan referensi:
- Matematika untuk SMP/MTs Kelas VIII oleh Erlangga
- Matematika untuk SMA/MA Kelas X oleh Erlangga
- Matematika untuk SMA/MA Kelas XI oleh Erlangga
Rekomendasi Artikel
Artikel online dapat menjadi sumber belajar yang mudah diakses dan praktis. Berikut beberapa situs web yang menyediakan artikel tentang nilai mutlak:
- Zenius: Situs web ini menyediakan artikel yang mudah dipahami dengan ilustrasi yang menarik.
- Ruangguru: Situs web ini menawarkan artikel tentang nilai mutlak yang lengkap dengan contoh soal dan pembahasan.
- GuruPendidikan: Situs web ini menyediakan artikel yang membahas konsep nilai mutlak secara detail.
Rekomendasi Video
Video pembelajaran dapat menjadi cara yang efektif untuk memahami konsep nilai mutlak. Berikut beberapa platform video pembelajaran yang bisa Anda akses:
- Khan Academy: Platform ini menyediakan video pembelajaran matematika yang lengkap dan mudah dipahami.
- Belajar Matematika: Channel YouTube ini menyediakan video pembelajaran tentang nilai mutlak dengan penjelasan yang detail dan mudah dipahami.
- MathGeeks: Channel YouTube ini menawarkan video pembelajaran tentang nilai mutlak dengan animasi dan ilustrasi yang menarik.
Rekomendasi Website
Selain artikel dan video, beberapa situs web menyediakan materi pembelajaran tentang nilai mutlak yang interaktif dan menyenangkan.
- GeoGebra: Situs web ini menyediakan aplikasi online untuk mempelajari matematika, termasuk nilai mutlak, dengan visualisasi yang interaktif.
- Desmos: Situs web ini menyediakan kalkulator online yang dapat digunakan untuk mempelajari konsep nilai mutlak dengan grafik dan animasi.
- Wolfram Alpha: Situs web ini menyediakan mesin pencari yang dapat digunakan untuk mencari informasi tentang nilai mutlak, termasuk rumus, contoh soal, dan solusi.
Terakhir
Memahami nilai mutlak tidak hanya membantu dalam menyelesaikan soal-soal matematika, tetapi juga membuka wawasan baru dalam memahami berbagai fenomena di sekitar kita. Dengan pemahaman yang mendalam, kamu dapat menyelesaikan masalah yang melibatkan nilai mutlak dengan lebih mudah dan percaya diri.





