Contoh soal dilatasi beserta jawabannya – Dilatasi, salah satu transformasi geometri, mungkin terdengar asing di telinga. Namun, konsep ini ternyata sangat dekat dengan kehidupan kita. Bayangkan ketika kita memperbesar atau memperkecil foto di ponsel, atau saat arsitek merancang bangunan dengan skala tertentu. Itulah contoh sederhana dari dilatasi, sebuah transformasi yang mengubah ukuran objek tanpa mengubah bentuknya.
Dalam artikel ini, kita akan menjelajahi dunia dilatasi dengan lebih dalam. Mulai dari definisi dan rumus, jenis-jenis dilatasi, contoh soal, hingga penerapannya dalam kehidupan sehari-hari. Siap untuk melangkah ke dunia transformasi geometri yang menarik?
Contoh Soal Dilatasi
Dilatasi adalah transformasi geometri yang mengubah ukuran suatu bangun tanpa mengubah bentuknya. Dilatasi dapat memperbesar atau memperkecil ukuran bangun, tergantung pada faktor skala yang digunakan. Faktor skala merupakan bilangan real yang menentukan perbandingan ukuran bangun hasil dilatasi dengan ukuran bangun asalnya. Jika faktor skala lebih besar dari 1, maka dilatasi akan memperbesar bangun. Sebaliknya, jika faktor skala lebih kecil dari 1, maka dilatasi akan memperkecil bangun. Dilatasi juga dapat didefinisikan sebagai perkalian vektor posisi titik dengan faktor skala tertentu.
Untuk memahami lebih lanjut tentang dilatasi, mari kita bahas beberapa contoh soal dan penyelesaiannya.
Contoh Soal Dilatasi
Berikut ini beberapa contoh soal dilatasi dengan tingkat kesulitan berbeda:
| No | Soal | Jawaban | Penjelasan |
|---|---|---|---|
| 1 | Sebuah titik A(2, 3) didilatasi dengan faktor skala 2 terhadap titik pusat O(0, 0). Tentukan koordinat bayangan titik A! | A'(4, 6) |
Untuk menentukan koordinat bayangan titik A, kita dapat menggunakan rumus dilatasi terhadap titik pusat O(0, 0):
dengan:
Dalam soal ini, A(2, 3), k = 2, dan O(0, 0). Maka:
Jadi, koordinat bayangan titik A adalah A'(4, 6). |
| 2 | Sebuah segitiga ABC dengan koordinat A(1, 2), B(3, 1), dan C(2, 4) didilatasi dengan faktor skala 1/2 terhadap titik pusat O(0, 0). Tentukan koordinat bayangan segitiga ABC! | A'(1/2, 1), B'(3/2, 1/2), C'(1, 2) |
Untuk menentukan koordinat bayangan segitiga ABC, kita dapat menggunakan rumus dilatasi terhadap titik pusat O(0, 0) untuk setiap titik sudutnya:
dengan:
Dalam soal ini, k = 1/2 dan O(0, 0). Maka:
Jadi, koordinat bayangan segitiga ABC adalah A'(1/2, 1), B'(3/2, 1/2), dan C'(1, 2). Contoh soal dilatasi beserta jawabannya memang sering muncul dalam pelajaran matematika, khususnya geometri. Soal-soal tersebut membantu kita memahami bagaimana sebuah objek dapat diperbesar atau diperkecil dengan faktor skala tertentu. Nah, berbicara soal kasus kehilangan dan berduka, kamu bisa menemukan contoh soal dan pembahasannya di contoh soal kasus kehilangan dan berduka. Sama seperti contoh soal dilatasi, contoh soal kasus kehilangan dan berduka juga membantu kita memahami konsep dan bagaimana menghadapinya. Kembali ke topik dilatasi, memahami konsep ini penting untuk menguasai materi geometri dan menyelesaikan soal-soal yang lebih kompleks. |
| 3 | Sebuah persegi panjang ABCD dengan koordinat A(1, 1), B(4, 1), C(4, 3), dan D(1, 3) didilatasi dengan faktor skala 3 terhadap titik pusat O(0, 0). Tentukan luas persegi panjang ABCD dan luas bayangannya! | Luas persegi panjang ABCD = 6 satuan luas, Luas bayangan = 54 satuan luas |
Untuk menentukan luas persegi panjang ABCD, kita dapat menggunakan rumus luas persegi panjang:
Panjang persegi panjang ABCD = 4 – 1 = 3 satuan Lebar persegi panjang ABCD = 3 – 1 = 2 satuan Maka luas persegi panjang ABCD = 3 * 2 = 6 satuan luas. Untuk menentukan luas bayangan persegi panjang ABCD, kita perlu menentukan koordinat bayangan setiap titik sudutnya terlebih dahulu. Kita dapat menggunakan rumus dilatasi terhadap titik pusat O(0, 0):
dengan:
Dalam soal ini, k = 3 dan O(0, 0). Maka:
Panjang bayangan persegi panjang ABCD = 12 – 3 = 9 satuan Lebar bayangan persegi panjang ABCD = 9 – 3 = 6 satuan Maka luas bayangan persegi panjang ABCD = 9 * 6 = 54 satuan luas. |
| 4 | Sebuah lingkaran dengan pusat O(2, 1) dan jari-jari 3 satuan didilatasi dengan faktor skala 2 terhadap titik pusat O(0, 0). Tentukan persamaan lingkaran hasil dilatasi! | (x – 4)² + (y – 2)² = 36 |
Untuk menentukan persamaan lingkaran hasil dilatasi, kita perlu menentukan koordinat pusat lingkaran hasil dilatasi dan jari-jari lingkaran hasil dilatasi terlebih dahulu. Kita dapat menggunakan rumus dilatasi terhadap titik pusat O(0, 0):
dengan:
Dalam soal ini, k = 2 dan O(0, 0). Maka:
Jari-jari lingkaran hasil dilatasi = 2 * 3 = 6 satuan Maka persamaan lingkaran hasil dilatasi adalah:
|
| 5 | Sebuah persegi panjang ABCD dengan koordinat A(1, 2), B(3, 2), C(3, 4), dan D(1, 4) didilatasi dengan faktor skala 2 terhadap titik pusat P(1, 1). Tentukan koordinat bayangan persegi panjang ABCD! | A'(1, 3), B'(3, 3), C'(3, 7), D'(1, 7) |
Untuk menentukan koordinat bayangan persegi panjang ABCD, kita dapat menggunakan rumus dilatasi terhadap titik pusat P(1, 1):
dengan:
Dalam soal ini, k = 2 dan P(1, 1). Maka:
Jadi, koordinat bayangan persegi panjang ABCD adalah A'(1, 3), B'(3, 3), C'(3, 7), dan D'(1, 7). |
Penerapan Dilatasi dalam Kehidupan Sehari-hari
Dilatasi merupakan transformasi geometri yang mengubah ukuran suatu objek tanpa mengubah bentuknya. Objek yang mengalami dilatasi dapat diperbesar atau diperkecil, tergantung pada faktor skala yang digunakan. Dilatasi memiliki banyak penerapan dalam kehidupan sehari-hari, mulai dari arsitektur hingga pembuatan peta.
Penerapan Dilatasi dalam Arsitektur
Dilatasi banyak digunakan dalam bidang arsitektur untuk mendesain bangunan dengan berbagai ukuran. Misalnya, arsitek dapat menggunakan dilatasi untuk memperbesar atau memperkecil model bangunan sebelum dibangun. Hal ini memungkinkan mereka untuk melihat bagaimana bangunan tersebut akan terlihat dalam skala sebenarnya dan untuk membuat penyesuaian yang diperlukan.
Penerapan Dilatasi dalam Pembuatan Peta
Dilatasi juga digunakan dalam pembuatan peta untuk mengubah ukuran objek geografis. Misalnya, peta dunia menggunakan dilatasi untuk memperkecil ukuran bumi sehingga dapat ditampilkan pada selembar kertas. Faktor skala yang digunakan dalam dilatasi ini menentukan seberapa kecil ukuran bumi yang ditampilkan pada peta.
Contoh Lain Penerapan Dilatasi
Selain dalam arsitektur dan pembuatan peta, dilatasi juga memiliki berbagai aplikasi lain dalam kehidupan sehari-hari. Berikut adalah beberapa contohnya:
- Fotografi: Dilatasi digunakan dalam fotografi untuk memperbesar atau memperkecil gambar. Misalnya, fotografer dapat menggunakan dilatasi untuk memperbesar wajah seseorang dalam foto atau untuk memperkecil objek yang terlalu besar dalam gambar.
- Desain Grafis: Dilatasi juga digunakan dalam desain grafis untuk mengubah ukuran logo, ilustrasi, dan elemen grafis lainnya. Misalnya, desainer grafis dapat menggunakan dilatasi untuk memperbesar logo agar terlihat lebih jelas pada papan reklame atau untuk memperkecil gambar agar dapat diunggah ke situs web.
- Teknik Mesin: Dilatasi digunakan dalam teknik mesin untuk mengubah ukuran komponen mesin. Misalnya, insinyur dapat menggunakan dilatasi untuk memperbesar atau memperkecil poros mesin agar sesuai dengan spesifikasi tertentu.
Dilatasi pada Transformasi Geometri
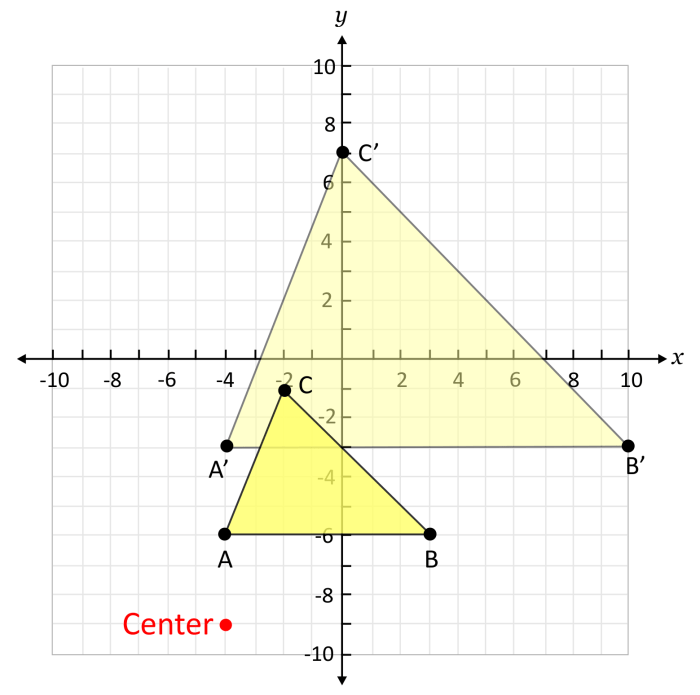
Dilatasi merupakan salah satu jenis transformasi geometri yang mengubah ukuran suatu bangun geometri tanpa mengubah bentuknya. Pada dilatasi, setiap titik pada bangun geometri akan diubah posisinya dengan faktor skala tertentu. Dilatasi dapat memperbesar atau memperkecil bangun geometri, tergantung pada nilai faktor skalanya.
Posisi Dilatasi dalam Transformasi Geometri
Dilatasi merupakan salah satu dari empat transformasi geometri dasar, yaitu:
- Translasi: Pergeseran bangun geometri tanpa mengubah ukuran dan bentuknya.
- Rotasi: Pemutaran bangun geometri terhadap titik tertentu dengan sudut tertentu.
- Refleksi: Pencerminan bangun geometri terhadap suatu garis.
- Dilatasi: Perubahan ukuran bangun geometri dengan faktor skala tertentu.
Perbandingan Dilatasi dengan Transformasi Geometri Lainnya
Dilatasi berbeda dengan transformasi geometri lainnya dalam hal perubahan ukuran bangun geometri. Translasi, rotasi, dan refleksi tidak mengubah ukuran bangun geometri, sedangkan dilatasi mengubah ukurannya. Berikut adalah perbandingan lebih detail:
| Transformasi | Perubahan Ukuran | Perubahan Bentuk | Contoh |
|---|---|---|---|
| Translasi | Tidak ada | Tidak ada | Pergeseran segitiga 5 satuan ke kanan dan 3 satuan ke atas |
| Rotasi | Tidak ada | Tidak ada | Pemutaran persegi 90 derajat searah jarum jam terhadap titik pusatnya |
| Refleksi | Tidak ada | Tidak ada | Pencerminan lingkaran terhadap sumbu-x |
| Dilatasi | Ada | Tidak ada | Perbesaran segitiga dengan faktor skala 2 |
Contoh Soal Gabungan Transformasi Geometri
Berikut adalah contoh soal yang melibatkan gabungan beberapa transformasi geometri, termasuk dilatasi:
“Sebuah segitiga ABC dengan titik A (1, 2), B (3, 4), dan C (5, 1) didilatasi dengan faktor skala 2 terhadap titik pusat (0, 0). Kemudian, hasil dilatasi tersebut ditranslasi 3 satuan ke kanan dan 2 satuan ke atas. Tentukan koordinat titik-titik segitiga ABC setelah dilatasi dan translasi.”
Penyelesaian:
1. Dilatasi:
– Titik A (1, 2) didilatasi dengan faktor skala 2 terhadap titik pusat (0, 0) menjadi A’ (2, 4).
– Titik B (3, 4) didilatasi dengan faktor skala 2 terhadap titik pusat (0, 0) menjadi B’ (6, 8).
– Titik C (5, 1) didilatasi dengan faktor skala 2 terhadap titik pusat (0, 0) menjadi C’ (10, 2).
2. Translasi:
– Titik A’ (2, 4) ditranslasi 3 satuan ke kanan dan 2 satuan ke atas menjadi A” (5, 6).
– Titik B’ (6, 8) ditranslasi 3 satuan ke kanan dan 2 satuan ke atas menjadi B” (9, 10).
– Titik C’ (10, 2) ditranslasi 3 satuan ke kanan dan 2 satuan ke atas menjadi C” (13, 4).
Jadi, koordinat titik-titik segitiga ABC setelah dilatasi dan translasi adalah A” (5, 6), B” (9, 10), dan C” (13, 4).
Dilatasi pada Ruang Tiga Dimensi
Dilatasi dalam geometri adalah transformasi yang mengubah ukuran suatu objek. Dalam ruang tiga dimensi, dilatasi dapat memperbesar atau memperkecil objek dengan faktor skala tertentu, tanpa mengubah bentuk aslinya. Bayangkan seperti membesar-kecilkan foto, tetapi dalam tiga dimensi!
Konsep Dilatasi pada Ruang Tiga Dimensi, Contoh soal dilatasi beserta jawabannya
Dilatasi pada ruang tiga dimensi adalah transformasi geometri yang mengubah ukuran objek dengan faktor skala tertentu, tanpa mengubah bentuk aslinya. Faktor skala ini menentukan seberapa besar objek tersebut diperbesar atau diperkecil. Jika faktor skala lebih besar dari 1, maka objek tersebut diperbesar. Sebaliknya, jika faktor skala kurang dari 1, maka objek tersebut diperkecil. Faktor skala 1 berarti objek tidak mengalami perubahan ukuran.
Ilustrasi Dilatasi pada Kubus
Untuk lebih memahami dilatasi, bayangkan sebuah kubus. Jika kita melakukan dilatasi pada kubus dengan faktor skala 2, maka setiap sisi kubus akan menjadi dua kali lebih panjang dari sebelumnya. Volume kubus juga akan meningkat menjadi delapan kali lipat dari volume semula. Sebaliknya, jika faktor skala adalah 1/2, maka setiap sisi kubus akan menjadi setengah lebih pendek dari sebelumnya, dan volume kubus akan menjadi seperdelapan dari volume semula. Bayangkan seperti membesar-kecilkan sebuah kotak mainan!
Rumus Umum Dilatasi pada Ruang Tiga Dimensi
Titik (x, y, z) setelah dilatasi dengan faktor skala k terhadap titik pusat (a, b, c) menjadi (kx + (1-k)a, ky + (1-k)b, kz + (1-k)c).
Rumus ini menunjukkan bahwa dilatasi pada ruang tiga dimensi dapat didefinisikan dengan faktor skala k dan titik pusat (a, b, c). Titik pusat ini adalah titik acuan yang digunakan untuk menentukan arah dan jarak dilatasi.
Dilatasi dan Inversinya
Dilatasi merupakan transformasi geometri yang mengubah ukuran suatu bangun geometri. Dilatasi dapat memperbesar atau memperkecil bangun geometri, dengan titik pusat dilatasi sebagai titik acuan.
Konsep Invers Dilatasi
Invers dilatasi adalah transformasi geometri yang “membalikkan” efek dilatasi. Artinya, jika suatu bangun geometri telah didilatasi, invers dilatasi akan mengembalikan bangun tersebut ke ukuran dan posisi semula.
Rumus Invers Dilatasi
Invers dilatasi didefinisikan dengan rumus berikut:
Dk-1(P) = (1/k) * P
di mana:
* Dk-1(P) adalah invers dilatasi titik P dengan faktor skala k.
* k adalah faktor skala dilatasi.
* P adalah titik yang didilatasi.
Contoh Soal Invers Dilatasi
Misalkan titik A(2, 4) didilatasi dengan faktor skala 3 terhadap titik pusat O(0, 0). Tentukan koordinat bayangan titik A setelah dilatasi dan koordinat titik A setelah dilakukan invers dilatasi.
Penyelesaian:
* Koordinat bayangan titik A setelah dilatasi dengan faktor skala 3 adalah:
A’ = 3 * A = 3 * (2, 4) = (6, 12)
* Koordinat titik A setelah dilakukan invers dilatasi dengan faktor skala 3 adalah:
A” = (1/3) * A’ = (1/3) * (6, 12) = (2, 4)
Jadi, koordinat titik A setelah dilakukan invers dilatasi adalah (2, 4), yang merupakan titik awal sebelum dilatasi.
Soal Dilatasi Tingkat Kesulitan Tinggi
Dilatasi adalah transformasi geometri yang mengubah ukuran suatu bangun geometri. Soal dilatasi tingkat kesulitan tinggi biasanya melibatkan kombinasi konsep dilatasi dengan konsep geometri lainnya, seperti kesebangunan, kongruensi, dan persamaan garis.
Contoh Soal Dilatasi Tingkat Kesulitan Tinggi
Berikut adalah contoh soal dilatasi tingkat kesulitan tinggi beserta jawaban dan penjelasannya:
Soal:
Sebuah segitiga ABC dengan titik A(1, 2), B(3, 1), dan C(2, 4) didilatasi dengan faktor skala k = 2 terhadap titik pusat O(0, 0). Tentukan persamaan garis yang melalui titik tengah sisi BC dan tegak lurus terhadap garis AB.
Jawaban:
1. Menentukan bayangan titik A, B, dan C:
– Bayangan titik A: A'(2k, 2k) = A'(2(2), 2(2)) = A'(4, 4)
– Bayangan titik B: B'(3k, k) = B'(3(2), 2) = B'(6, 2)
– Bayangan titik C: C'(2k, 4k) = C'(2(2), 4(2)) = C'(4, 8)
2. Menentukan titik tengah sisi BC:
– Titik tengah sisi BC adalah ((6+4)/2, (2+8)/2) = (5, 5)
3. Menentukan gradien garis AB:
– Gradien garis AB = (1-2)/(3-1) = -1/2
4. Menentukan gradien garis tegak lurus terhadap AB:
– Karena garis tegak lurus, maka perkalian gradien kedua garis sama dengan -1.
– Gradien garis tegak lurus = 2
5. Menentukan persamaan garis yang melalui titik tengah BC dan tegak lurus terhadap AB:
– Menggunakan rumus persamaan garis y – y1 = m(x – x1), dengan m = 2 dan (x1, y1) = (5, 5), maka persamaan garisnya adalah:
– y – 5 = 2(x – 5)
– y – 5 = 2x – 10
– y = 2x – 5
Jadi, persamaan garis yang melalui titik tengah sisi BC dan tegak lurus terhadap garis AB adalah y = 2x – 5.
Strategi Penyelesaian Soal Dilatasi Tingkat Kesulitan Tinggi
- Memahami konsep dilatasi dan konsep geometri lainnya yang terkait: Pahami dengan baik konsep dilatasi, termasuk faktor skala dan titik pusat dilatasi. Selain itu, pahami juga konsep geometri lainnya yang mungkin terlibat dalam soal, seperti kesebangunan, kongruensi, dan persamaan garis.
- Menganalisis soal dengan cermat: Bacalah soal dengan teliti dan identifikasi informasi penting yang diberikan, seperti titik-titik koordinat, faktor skala, dan titik pusat dilatasi. Perhatikan juga pertanyaan yang diajukan.
- Menggunakan rumus dan teorema yang tepat: Terapkan rumus dan teorema yang relevan dengan konsep dilatasi dan geometri lainnya untuk menyelesaikan soal.
- Melakukan langkah-langkah secara sistematis: Pecahkan soal secara bertahap dan sistematis, mulai dari menentukan bayangan titik-titik, kemudian menghitung jarak, gradien, dan persamaan garis yang diminta.
- Memeriksa kembali jawaban: Setelah menyelesaikan soal, periksa kembali jawaban Anda dengan cermat untuk memastikan bahwa jawaban Anda benar dan masuk akal.
Tips Tambahan
- Berlatih secara rutin: Semakin banyak Anda berlatih menyelesaikan soal dilatasi, semakin mahir Anda dalam memahami konsep dan strategi penyelesaiannya.
- Meminta bantuan guru atau tutor: Jangan ragu untuk meminta bantuan guru atau tutor jika Anda mengalami kesulitan dalam memahami konsep atau menyelesaikan soal dilatasi.
- Mencari sumber belajar tambahan: Gunakan buku, website, atau video pembelajaran untuk mempelajari lebih lanjut tentang dilatasi dan konsep geometri lainnya.
Penutupan: Contoh Soal Dilatasi Beserta Jawabannya
Memahami dilatasi tidak hanya penting dalam mempelajari matematika, tetapi juga dalam berbagai bidang seperti arsitektur, desain grafis, dan bahkan pembuatan peta. Dengan memahami konsep dasar dilatasi, kita dapat lebih mudah memahami dan menyelesaikan berbagai masalah yang melibatkan transformasi geometri. Jadi, jangan ragu untuk mempraktikkan contoh soal yang telah dibahas dan teruslah belajar tentang dunia geometri yang penuh keajaiban!





