Contoh soal dilatasi kelas 11 – Dilatasi, sebuah transformasi geometri yang memindahkan titik-titik pada bidang dengan memperbesar atau memperkecil ukurannya, menjadi topik menarik dalam pembelajaran matematika kelas 11. Melalui proses dilatasi, kita dapat memahami bagaimana bentuk dan ukuran suatu objek berubah, bahkan terkadang menjadi lebih menarik!
Dalam artikel ini, kita akan menjelajahi contoh soal dilatasi yang melibatkan penentuan bayangan titik, garis, dan bangun datar. Kita akan mempelajari rumus dilatasi, sifat-sifatnya, dan bagaimana dilatasi diterapkan dalam kehidupan nyata. Siap-siap untuk mengasah kemampuan berpikir kritis dan visualisasi geometri!
Pengertian Dilatasi
Dilatasi merupakan salah satu transformasi geometri yang mengubah ukuran suatu bangun geometri. Proses dilatasi ini dapat memperbesar atau memperkecil ukuran bangun geometri, namun tetap mempertahankan bentuk aslinya. Proses dilatasi juga dikenal sebagai transformasi kesebangunan, karena bangun geometri yang dihasilkan melalui dilatasi akan sebangun dengan bangun geometri awal. Dilatasi dapat diilustrasikan dengan cara memperbesar atau memperkecil foto pada perangkat lunak pengolah gambar.
Jenis-jenis Dilatasi Berdasarkan Faktor Skala
Dilatasi diklasifikasikan berdasarkan faktor skala (k) yang digunakan. Faktor skala menentukan seberapa besar atau kecil bangun geometri yang dihasilkan dibandingkan dengan bangun geometri awal.
Contoh soal dilatasi kelas 11 biasanya melibatkan penggambaran transformasi geometri. Nah, kalau kamu mau latihan soal yang sedikit berbeda, coba cek contoh soal sinonim di sini. Soalnya, memahami sinonim juga penting dalam memahami konsep matematika, lho! Misalnya, “pergeseran” bisa diartikan sebagai “translasi”, yang keduanya berhubungan dengan transformasi geometri dalam dilatasi.
- Jika faktor skala (k) lebih besar dari 1 (k > 1), maka dilatasi disebut dilatasi pembesaran. Bangun geometri yang dihasilkan akan lebih besar daripada bangun geometri awal.
- Jika faktor skala (k) sama dengan 1 (k = 1), maka dilatasi disebut dilatasi identitas. Bangun geometri yang dihasilkan akan sama dengan bangun geometri awal.
- Jika faktor skala (k) berada di antara 0 dan 1 (0 < k < 1), maka dilatasi disebut dilatasi pengecilan. Bangun geometri yang dihasilkan akan lebih kecil daripada bangun geometri awal.
- Jika faktor skala (k) kurang dari 0 (k < 0), maka dilatasi disebut dilatasi dengan faktor skala negatif. Bangun geometri yang dihasilkan akan diputar 180 derajat dan diperbesar atau diperkecil tergantung pada nilai absolut dari faktor skala.
Contoh Ilustrasi Dilatasi
Berikut ini adalah contoh ilustrasi dilatasi dengan faktor skala positif dan negatif:
Dilatasi dengan Faktor Skala Positif
Misalkan kita memiliki segitiga ABC dengan titik-titik sudut A(1, 2), B(3, 1), dan C(2, 4). Kita ingin melakukan dilatasi terhadap segitiga ABC dengan faktor skala 2. Titik pusat dilatasi adalah titik O(0, 0).
Untuk melakukan dilatasi, kita dapat menggunakan rumus berikut:
A'(2 * 1, 2 * 2) = A'(2, 4)
B'(2 * 3, 2 * 1) = B'(6, 2)
C'(2 * 2, 2 * 4) = C'(4, 8)
Hasil dilatasi segitiga ABC dengan faktor skala 2 adalah segitiga A’B’C’ dengan titik-titik sudut A'(2, 4), B'(6, 2), dan C'(4, 8). Segitiga A’B’C’ lebih besar daripada segitiga ABC, namun bentuknya tetap sama.
Dilatasi dengan Faktor Skala Negatif
Misalkan kita memiliki persegi panjang ABCD dengan titik-titik sudut A(1, 1), B(3, 1), C(3, 3), dan D(1, 3). Kita ingin melakukan dilatasi terhadap persegi panjang ABCD dengan faktor skala -2. Titik pusat dilatasi adalah titik O(0, 0).
Untuk melakukan dilatasi, kita dapat menggunakan rumus berikut:
A'(-2 * 1, -2 * 1) = A'(-2, -2)
B'(-2 * 3, -2 * 1) = B'(-6, -2)
C'(-2 * 3, -2 * 3) = C'(-6, -6)
D'(-2 * 1, -2 * 3) = D'(-2, -6)
Hasil dilatasi persegi panjang ABCD dengan faktor skala -2 adalah persegi panjang A’B’C’D’ dengan titik-titik sudut A'(-2, -2), B'(-6, -2), C'(-6, -6), dan D'(-2, -6). Persegi panjang A’B’C’D’ lebih besar daripada persegi panjang ABCD dan diputar 180 derajat.
Rumus Dilatasi
Dilatasi adalah transformasi geometri yang mengubah ukuran suatu bangun geometri dengan faktor skala tertentu. Faktor skala menentukan seberapa besar atau kecil bangun tersebut akan berubah. Dalam dilatasi, titik pusat dilatasi adalah titik tetap yang digunakan sebagai titik acuan untuk menentukan posisi bayangan.
Rumus Umum Dilatasi
Rumus umum dilatasi dengan pusat (a,b) dan faktor skala k adalah:
D(a,b),k (x,y) = ((k(x-a)+a), (k(y-b)+b))
Rumus ini digunakan untuk menentukan koordinat bayangan titik (x,y) setelah dilatasi.
Cara Menggunakan Rumus Dilatasi
Rumus dilatasi digunakan untuk menentukan koordinat bayangan titik dengan langkah-langkah berikut:
- Tentukan titik pusat dilatasi (a,b) dan faktor skala k.
- Tentukan koordinat titik yang akan didilatasi (x,y).
- Substitusikan nilai a, b, k, x, dan y ke dalam rumus dilatasi.
- Hitung hasil dari rumus untuk mendapatkan koordinat bayangan titik.
Contoh Penerapan Rumus Dilatasi
Misalnya, kita ingin mencari bayangan titik (2,3) dengan pusat (1,1) dan faktor skala 2. Dengan menggunakan rumus dilatasi, kita dapat menghitung koordinat bayangan titik sebagai berikut:
- Tentukan titik pusat dilatasi (a,b) = (1,1) dan faktor skala k = 2.
- Tentukan koordinat titik yang akan didilatasi (x,y) = (2,3).
- Substitusikan nilai a, b, k, x, dan y ke dalam rumus dilatasi:
D(1,1),2 (2,3) = ((2(2-1)+1), (2(3-1)+1)) = (3,5)
- Hasil perhitungan menunjukkan bahwa bayangan titik (2,3) setelah dilatasi dengan pusat (1,1) dan faktor skala 2 adalah (3,5).
Sifat-Sifat Dilatasi: Contoh Soal Dilatasi Kelas 11
Dilatasi adalah transformasi geometri yang mengubah ukuran suatu bangun geometri, baik memperbesar maupun memperkecil, dengan tetap mempertahankan bentuk aslinya. Dilatasi memiliki beberapa sifat yang perlu dipahami untuk memahami bagaimana transformasi ini memengaruhi objek geometri.
Perubahan Ukuran dan Bentuk
Dilatasi mengubah ukuran bangun geometri, tetapi tidak mengubah bentuknya. Artinya, bentuk bangun geometri tetap sama, hanya ukurannya yang berubah. Faktor skala yang digunakan dalam dilatasi menentukan seberapa besar atau kecil ukuran bangun geometri setelah dilatasi.
Pengaruh Dilatasi terhadap Jarak antara Titik-Titik
Dilatasi juga memengaruhi jarak antara titik-titik dalam bangun geometri. Jarak antara dua titik setelah dilatasi akan menjadi faktor skala kali jarak antara titik-titik tersebut sebelum dilatasi.
Misalnya, jika faktor skala dilatasi adalah 2, maka jarak antara dua titik setelah dilatasi akan menjadi dua kali jarak antara titik-titik tersebut sebelum dilatasi.
Pengaruh Dilatasi terhadap Sudut-Sudut
Dilatasi tidak memengaruhi besar sudut-sudut dalam bangun geometri. Sudut-sudut dalam bangun geometri tetap sama sebelum dan sesudah dilatasi.
Misalnya, jika suatu segitiga memiliki sudut 60°, 80°, dan 40°, maka setelah dilatasi, segitiga tersebut akan tetap memiliki sudut 60°, 80°, dan 40°.
Contoh Soal Dilatasi
Dilatasi merupakan salah satu transformasi geometri yang mengubah ukuran suatu bangun tanpa mengubah bentuknya. Dilatasi dapat memperbesar atau memperkecil ukuran bangun.
Contoh Soal Dilatasi Titik
Berikut adalah contoh soal dilatasi yang melibatkan penentuan bayangan titik:
| Soal | Penyelesaian | Ilustrasi | Kesimpulan |
|---|---|---|---|
| Tentukan bayangan titik A(2, 3) oleh dilatasi dengan faktor skala 2 terhadap titik pusat O(0, 0)! |
|
Gambarlah titik A(2, 3) dan titik pusat O(0, 0). Kemudian, perpanjang garis OA hingga mencapai titik A’ yang terletak di sisi yang sama dengan A terhadap O. Titik A’ merupakan bayangan dari titik A. | Bayangan titik A(2, 3) oleh dilatasi dengan faktor skala 2 terhadap titik pusat O(0, 0) adalah A'(4, 6). |
Contoh Soal Dilatasi Garis
Berikut adalah contoh soal dilatasi yang melibatkan penentuan bayangan garis:
| Soal | Penyelesaian | Ilustrasi | Kesimpulan |
|---|---|---|---|
| Tentukan bayangan garis y = 2x + 1 oleh dilatasi dengan faktor skala 3 terhadap titik pusat O(0, 0)! |
|
Gambarlah garis y = 2x + 1 dan titik pusat O(0, 0). Kemudian, tentukan bayangan titik A dan B pada garis y = 2x + 1 oleh dilatasi dengan faktor skala 3 terhadap titik pusat O(0, 0). Hubungkan titik A’ dan B’ untuk mendapatkan bayangan garis y = 2x + 1. | Bayangan garis y = 2x + 1 oleh dilatasi dengan faktor skala 3 terhadap titik pusat O(0, 0) adalah garis yang melalui titik A'(0, 3) dan B'(3, 9). |
Contoh Soal Dilatasi Bangun Datar
Berikut adalah contoh soal dilatasi yang melibatkan penentuan bayangan bangun datar:
| Soal | Penyelesaian | Ilustrasi | Kesimpulan |
|---|---|---|---|
| Tentukan bayangan segitiga ABC dengan titik-titik sudut A(1, 2), B(3, 1), dan C(2, 4) oleh dilatasi dengan faktor skala 2 terhadap titik pusat O(0, 0)! |
|
Gambarlah segitiga ABC dan titik pusat O(0, 0). Kemudian, tentukan bayangan titik A, B, dan C pada segitiga ABC oleh dilatasi dengan faktor skala 2 terhadap titik pusat O(0, 0). Hubungkan titik A’, B’, dan C’ untuk mendapatkan bayangan segitiga ABC. | Bayangan segitiga ABC oleh dilatasi dengan faktor skala 2 terhadap titik pusat O(0, 0) adalah segitiga A’B’C’ dengan titik-titik sudut A'(2, 4), B'(6, 2), dan C'(4, 8). |
Penerapan Dilatasi
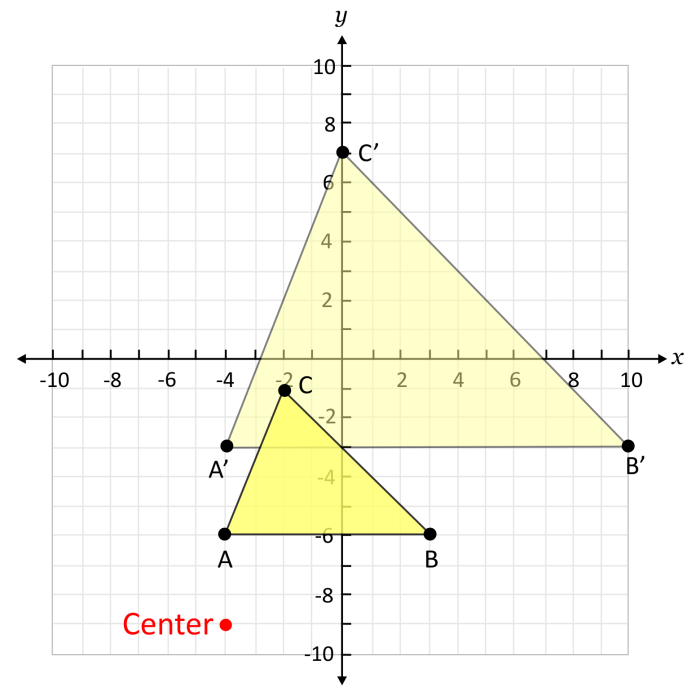
Dilatasi adalah transformasi geometri yang mengubah ukuran suatu bangun geometri tanpa mengubah bentuknya. Dilatasi dapat memperbesar atau memperkecil ukuran bangun geometri, tergantung pada faktor skalanya.
Penerapan Dilatasi dalam Kehidupan Sehari-hari
Dilatasi memiliki banyak penerapan dalam kehidupan sehari-hari. Berikut beberapa contohnya:
- Pembesaran Foto: Saat kita memperbesar atau memperkecil foto, kita menggunakan prinsip dilatasi. Faktor skala menentukan seberapa besar atau kecil foto tersebut.
- Pembesaran atau Pengecilan Peta: Peta dibuat dengan menggunakan prinsip dilatasi. Peta dapat memperbesar atau memperkecil ukuran suatu wilayah untuk memudahkan pembacaan.
- Pembuatan Model: Pembuatan model seperti miniatur mobil atau pesawat menggunakan prinsip dilatasi. Faktor skala menentukan seberapa besar atau kecil model tersebut dibandingkan dengan objek aslinya.
Penerapan Dilatasi dalam Bidang Desain Grafis, Contoh soal dilatasi kelas 11
Dalam desain grafis, dilatasi digunakan untuk:
- Memperbesar atau Memperkecil Gambar: Desainer grafis sering menggunakan dilatasi untuk memperbesar atau memperkecil gambar sesuai dengan kebutuhan.
- Membuat Efek Perspektif: Dilatasi dapat digunakan untuk membuat efek perspektif pada gambar, seperti membuat objek tampak lebih jauh atau lebih dekat.
- Membuat Efek Warp: Dilatasi dapat digunakan untuk membuat efek warp, yaitu mengubah bentuk suatu objek dengan cara meregangkan atau menekan bagian tertentu dari objek tersebut.
Penerapan Dilatasi dalam Bidang Arsitektur
Dilatasi juga memiliki peran penting dalam bidang arsitektur. Berikut beberapa contohnya:
- Perencanaan Tata Letak Bangunan: Dilatasi dapat digunakan untuk memperbesar atau memperkecil skala denah bangunan, sehingga arsitek dapat melihat dan merencanakan tata letak bangunan secara lebih detail.
- Pembuatan Model Bangunan: Dilatasi digunakan untuk membuat model bangunan, baik untuk presentasi maupun untuk keperluan konstruksi.
- Perancangan Interior: Dilatasi dapat digunakan untuk memperbesar atau memperkecil skala desain interior, sehingga arsitek dapat melihat dan merencanakan tata letak interior secara lebih detail.
Ulasan Penutup
Dengan memahami konsep dilatasi dan menyelesaikan contoh soal, kita tidak hanya meningkatkan pemahaman geometri, tetapi juga membuka wawasan tentang aplikasi transformasi ini dalam berbagai bidang. Mulai dari desain grafis hingga arsitektur, dilatasi memainkan peran penting dalam membentuk dunia di sekitar kita. Mari terus menggali dunia geometri dan menemukan keajaiban transformasi yang menakjubkan!





