Contoh soal ekonometrika – Ekonometrika, ilmu yang menggabungkan teori ekonomi dengan metode statistik, memungkinkan kita untuk menganalisis data ekonomi dengan lebih mendalam. Bayangkan, Anda ingin mengetahui apakah ada hubungan antara tingkat pendidikan dan pendapatan seseorang. Ekonometrika dapat membantu Anda menguji hipotesis tersebut dan bahkan memprediksi pendapatan seseorang berdasarkan tingkat pendidikannya.
Dalam artikel ini, kita akan membahas berbagai contoh soal ekonometrika yang mencakup analisis regresi linier sederhana, regresi linier berganda, dan model ekonometrika non-linier. Dengan mempelajari contoh-contoh soal ini, Anda akan memahami bagaimana ekonometrika dapat diterapkan untuk menyelesaikan berbagai masalah ekonomi dan bisnis.
Pengertian Ekonometrika
Ekonometrika merupakan cabang ilmu ekonomi yang menggabungkan teori ekonomi, matematika, dan statistika untuk menganalisis data ekonomi dan menguji hipotesis ekonomi. Dengan kata lain, ekonometrika adalah alat yang digunakan untuk mengukur dan menguji hubungan antar variabel ekonomi di dunia nyata.
Definisi Ekonometrika
Ekonometrika adalah ilmu yang menggabungkan teori ekonomi, matematika, dan statistika untuk menguji dan mengukur hubungan antar variabel ekonomi. Tujuannya adalah untuk membangun model kuantitatif yang dapat menjelaskan fenomena ekonomi dan membuat prediksi yang akurat.
Tujuan Ekonometrika
Tujuan utama ekonometrika adalah untuk:
- Menguji teori ekonomi dengan menggunakan data ekonomi nyata.
- Membuat prediksi tentang variabel ekonomi di masa depan.
- Membuat kebijakan ekonomi yang lebih efektif.
- Menganalisis hubungan sebab-akibat antar variabel ekonomi.
Contoh Aplikasi Ekonometrika
Ekonometrika dapat diaplikasikan dalam berbagai bidang studi ekonomi, seperti:
- Analisis pasar: Untuk memprediksi permintaan dan penawaran terhadap suatu produk atau jasa.
- Analisis kebijakan: Untuk mengevaluasi efektivitas kebijakan ekonomi, seperti kebijakan fiskal atau moneter.
- Analisis keuangan: Untuk memprediksi pergerakan harga saham atau nilai tukar mata uang.
- Analisis tenaga kerja: Untuk mengkaji hubungan antara upah dan produktivitas tenaga kerja.
Sebagai contoh, ekonometrika dapat digunakan untuk menganalisis hubungan antara tingkat pengangguran dan inflasi. Model ekonometrika dapat dibangun untuk menguji apakah terdapat hubungan yang signifikan antara kedua variabel tersebut dan bagaimana hubungan tersebut berubah seiring waktu. Model ini kemudian dapat digunakan untuk memprediksi tingkat inflasi di masa depan berdasarkan tingkat pengangguran yang diproyeksikan.
Jenis-Jenis Model Ekonometrika
Ekonometrika merupakan cabang ilmu ekonomi yang menggabungkan teori ekonomi, statistik, dan matematika untuk menganalisis data ekonomi dan membangun model kuantitatif untuk memahami dan memprediksi fenomena ekonomi. Model ekonometrika memainkan peran penting dalam pengambilan keputusan ekonomi, baik di tingkat mikro maupun makro.
Model ekonometrika dibagi menjadi beberapa jenis, yang masing-masing memiliki karakteristik, keunggulan, dan kekurangannya sendiri. Berikut ini adalah beberapa jenis model ekonometrika yang umum digunakan:
Model Regresi Linear
Model regresi linear adalah model ekonometrika yang paling dasar dan paling sering digunakan. Model ini mengasumsikan hubungan linear antara variabel dependen dan variabel independen.
- Model regresi linear sederhana: Model ini hanya memiliki satu variabel independen.
- Model regresi linear berganda: Model ini memiliki lebih dari satu variabel independen.
Rumus model regresi linear sederhana:
Y = β0 + β1X + ε
di mana:
- Y adalah variabel dependen
- X adalah variabel independen
- β0 adalah konstanta
- β1 adalah koefisien regresi
- ε adalah error term
Contoh model regresi linear sederhana:
Misalnya, kita ingin memprediksi jumlah permintaan suatu produk berdasarkan harga produk tersebut. Variabel dependen adalah jumlah permintaan, sedangkan variabel independen adalah harga produk. Model regresi linear sederhana dapat digunakan untuk memprediksi jumlah permintaan berdasarkan harga produk.
Model Regresi Non-Linear
Model regresi non-linear adalah model ekonometrika yang mengasumsikan hubungan non-linear antara variabel dependen dan variabel independen.
- Model regresi polinomial: Model ini menggunakan variabel independen yang dipangkatkan ke tingkat yang lebih tinggi.
- Model regresi eksponensial: Model ini mengasumsikan hubungan eksponensial antara variabel dependen dan variabel independen.
- Model regresi logistik: Model ini digunakan untuk memprediksi probabilitas suatu kejadian, seperti probabilitas seseorang membeli produk.
Rumus model regresi polinomial:
Y = β0 + β1X + β2X2 + … + βnXn + ε
di mana:
- Y adalah variabel dependen
- X adalah variabel independen
- β0, β1, …, βn adalah koefisien regresi
- ε adalah error term
Contoh model regresi non-linear:
Misalnya, kita ingin memprediksi tingkat konsumsi rumah tangga berdasarkan pendapatan rumah tangga. Hubungan antara konsumsi dan pendapatan mungkin tidak selalu linear. Model regresi non-linear dapat digunakan untuk memprediksi konsumsi berdasarkan pendapatan, dengan mempertimbangkan hubungan non-linear yang mungkin terjadi.
Model Persamaan Simultan
Model persamaan simultan adalah model ekonometrika yang digunakan untuk menganalisis sistem persamaan yang saling terkait. Model ini sering digunakan untuk menganalisis pasar ekonomi, di mana permintaan dan penawaran saling memengaruhi.
- Model persamaan simultan dua persamaan: Model ini memiliki dua persamaan yang saling terkait.
- Model persamaan simultan tiga persamaan atau lebih: Model ini memiliki tiga persamaan atau lebih yang saling terkait.
Contoh model persamaan simultan dua persamaan:
Qd = a0 + a1P + a2Y + ε1
Qs = b0 + b1P + ε2
di mana:
- Qd adalah jumlah permintaan
- Qs adalah jumlah penawaran
- P adalah harga
- Y adalah pendapatan
- a0, a1, a2, b0, b1 adalah koefisien regresi
- ε1, ε2 adalah error term
Contoh model persamaan simultan:
Misalnya, kita ingin menganalisis pasar tenaga kerja, di mana jumlah permintaan tenaga kerja dipengaruhi oleh upah dan jumlah penawaran tenaga kerja juga dipengaruhi oleh upah. Model persamaan simultan dapat digunakan untuk menganalisis hubungan antara permintaan dan penawaran tenaga kerja, serta dampak upah terhadap keduanya.
Model Deret Waktu
Model deret waktu adalah model ekonometrika yang digunakan untuk menganalisis data yang dikumpulkan secara berkala, seperti data bulanan, triwulanan, atau tahunan. Model ini sering digunakan untuk memprediksi variabel ekonomi di masa depan, seperti inflasi atau pertumbuhan ekonomi.
- Model autoregresif (AR): Model ini mengasumsikan bahwa nilai variabel dependen pada periode saat ini dipengaruhi oleh nilai variabel dependen pada periode sebelumnya.
- Model moving average (MA): Model ini mengasumsikan bahwa nilai variabel dependen pada periode saat ini dipengaruhi oleh nilai error term pada periode sebelumnya.
- Model autoregresif moving average (ARMA): Model ini menggabungkan model AR dan MA.
Rumus model autoregresif (AR):
Yt = β0 + β1Yt-1 + εt
di mana:
- Yt adalah nilai variabel dependen pada periode t
- Yt-1 adalah nilai variabel dependen pada periode t-1
- β0, β1 adalah koefisien regresi
- εt adalah error term pada periode t
Contoh model deret waktu:
Misalnya, kita ingin memprediksi tingkat inflasi di masa depan. Model deret waktu dapat digunakan untuk memprediksi inflasi berdasarkan data inflasi pada periode sebelumnya.
Model Data Panel
Model data panel adalah model ekonometrika yang menggabungkan data cross-sectional dan data deret waktu. Model ini sering digunakan untuk menganalisis data yang dikumpulkan dari beberapa individu, perusahaan, atau negara selama beberapa periode waktu.
- Model efek tetap: Model ini mengasumsikan bahwa efek individu atau perusahaan bersifat konstan selama periode waktu yang diamati.
- Model efek acak: Model ini mengasumsikan bahwa efek individu atau perusahaan bersifat acak.
Rumus model data panel efek tetap:
Yit = β0 + β1Xit + αi + εit
di mana:
- Yit adalah nilai variabel dependen untuk individu i pada periode t
- Xit adalah nilai variabel independen untuk individu i pada periode t
- β0, β1 adalah koefisien regresi
- αi adalah efek tetap untuk individu i
- εit adalah error term untuk individu i pada periode t
Contoh model data panel:
Misalnya, kita ingin menganalisis pengaruh pendidikan terhadap pendapatan, dengan menggunakan data dari beberapa individu selama beberapa tahun. Model data panel dapat digunakan untuk menganalisis pengaruh pendidikan terhadap pendapatan, dengan mempertimbangkan efek individu yang mungkin berbeda.
Tabel Perbandingan Jenis Model Ekonometrika, Contoh soal ekonometrika
| Jenis Model | Karakteristik | Keunggulan | Kekurangan |
|---|---|---|---|
| Regresi Linear | Hubungan linear antara variabel dependen dan variabel independen | Mudah dipahami dan diinterpretasikan | Mungkin tidak sesuai untuk hubungan non-linear |
| Regresi Non-Linear | Hubungan non-linear antara variabel dependen dan variabel independen | Dapat menangkap hubungan non-linear yang kompleks | Lebih kompleks dan sulit diinterpretasikan |
| Persamaan Simultan | Sistem persamaan yang saling terkait | Dapat menganalisis hubungan timbal balik antara variabel | Lebih kompleks dan sulit untuk dipecahkan |
| Deret Waktu | Data yang dikumpulkan secara berkala | Dapat memprediksi variabel ekonomi di masa depan | Membutuhkan data deret waktu yang panjang |
| Data Panel | Data cross-sectional dan data deret waktu | Dapat menganalisis pengaruh individu atau perusahaan | Lebih kompleks dan membutuhkan data yang lebih banyak |
Langkah-Langkah Ekonometrika
Ekonometrika merupakan cabang ilmu ekonomi yang menggabungkan teori ekonomi, matematika, dan statistika untuk menganalisis data ekonomi dan menguji hipotesis ekonomi. Proses membangun model ekonometrika melibatkan serangkaian langkah sistematis yang memastikan hasil analisis yang akurat dan bermakna. Berikut adalah langkah-langkah dalam membangun model ekonometrika:
1. Perumusan Masalah dan Definisi Variabel
Langkah pertama dalam membangun model ekonometrika adalah merumuskan masalah yang ingin dikaji dan mendefinisikan variabel-variabel yang terlibat. Rumusan masalah yang jelas dan spesifik akan membantu dalam menentukan variabel-variabel yang relevan dan membangun model yang tepat. Misalnya, jika ingin menganalisis pengaruh tingkat suku bunga terhadap pertumbuhan ekonomi, maka masalahnya adalah hubungan antara tingkat suku bunga dan pertumbuhan ekonomi, dan variabel-variabel yang terlibat adalah tingkat suku bunga (variabel independen) dan pertumbuhan ekonomi (variabel dependen).
2. Pengumpulan Data
Setelah mendefinisikan variabel, langkah selanjutnya adalah mengumpulkan data yang diperlukan untuk analisis. Data dapat diperoleh dari berbagai sumber, seperti data sekunder (data yang sudah dikumpulkan oleh lembaga lain, seperti Badan Pusat Statistik) atau data primer (data yang dikumpulkan sendiri melalui survei atau eksperimen). Penting untuk memastikan bahwa data yang dikumpulkan akurat, reliabel, dan representatif untuk populasi yang ingin dikaji.
3. Analisis Deskriptif
Analisis deskriptif dilakukan untuk memahami karakteristik data yang dikumpulkan. Analisis ini meliputi penghitungan statistik deskriptif, seperti rata-rata, standar deviasi, dan korelasi, serta visualisasi data melalui grafik dan tabel. Analisis deskriptif membantu dalam mendapatkan gambaran awal tentang data dan mengidentifikasi pola atau tren yang mungkin terjadi.
4. Spesifikasi Model
Langkah selanjutnya adalah menentukan model ekonometrika yang akan digunakan untuk menganalisis data. Model ekonometrika adalah representasi matematis dari hubungan antara variabel-variabel yang dikaji. Pemilihan model yang tepat sangat penting karena akan menentukan interpretasi hasil analisis. Terdapat berbagai jenis model ekonometrika, seperti model regresi linear, model regresi non-linear, model autoregresif, dan model persamaan simultan. Pemilihan model tergantung pada jenis data, variabel yang terlibat, dan tujuan analisis.
5. Estimasi Parameter Model
Setelah model ekonometrika ditentukan, langkah selanjutnya adalah mengestimasi parameter model. Estimasi parameter dilakukan dengan menggunakan metode statistik yang sesuai, seperti metode kuadrat terkecil (Ordinary Least Squares – OLS). Metode OLS mencari nilai parameter yang meminimalkan selisih antara nilai prediksi model dan nilai sebenarnya dari variabel dependen. Hasil estimasi parameter menunjukkan hubungan antara variabel-variabel yang dikaji.
6. Uji Hipotesis
Setelah parameter model diestimasi, langkah selanjutnya adalah menguji hipotesis yang dirumuskan dalam masalah. Uji hipotesis bertujuan untuk menentukan apakah hubungan antara variabel-variabel yang dikaji signifikan secara statistik. Uji hipotesis dapat dilakukan dengan menggunakan uji t, uji F, atau uji statistik lainnya. Hasil uji hipotesis akan menunjukkan apakah hipotesis yang dirumuskan dapat diterima atau ditolak.
7. Interpretasi Hasil
Langkah terakhir dalam membangun model ekonometrika adalah menginterpretasi hasil analisis. Interpretasi hasil harus dilakukan dengan hati-hati dan mempertimbangkan konteks masalah yang dikaji. Hasil analisis dapat digunakan untuk memahami hubungan antara variabel-variabel yang dikaji, menguji hipotesis ekonomi, dan memberikan rekomendasi kebijakan.
Contoh soal ekonometrika seringkali menuntut pemahaman mendalam tentang konsep statistik dan model ekonomi. Nah, untuk memahami konsep-konsep tersebut, contoh soal dan jawaban sistem pelumasan seperti yang tersedia di contoh soal dan jawaban sistem pelumasan bisa menjadi bahan belajar yang menarik.
Sistem pelumasan sendiri merupakan salah satu contoh aplikasi ilmu teknik yang memiliki keterkaitan erat dengan konsep ekonomi, sehingga bisa membantu dalam memahami bagaimana penerapan teori ekonomi dalam dunia nyata.
8. Evaluasi Model
Setelah model ekonometrika dibangun, penting untuk mengevaluasi keakuratan dan kesesuaian model. Evaluasi model dilakukan dengan melihat berbagai aspek, seperti statistik goodness-of-fit (R-squared, adjusted R-squared), uji autokorelasi, uji heteroskedastisitas, dan uji multikolinearitas. Hasil evaluasi model akan menunjukkan apakah model yang dibangun sudah sesuai dengan data dan dapat digunakan untuk memprediksi atau menjelaskan fenomena ekonomi yang dikaji.
9. Penerapan Model
Setelah model ekonometrika divalidasi, model dapat diterapkan untuk berbagai tujuan, seperti memprediksi nilai variabel dependen, menguji hipotesis ekonomi, atau memberikan rekomendasi kebijakan. Penerapan model harus dilakukan dengan hati-hati dan mempertimbangkan konteks masalah yang dikaji.
10. Perbaikan Model
Model ekonometrika yang dibangun mungkin tidak sempurna dan dapat diubah atau diperbaiki berdasarkan hasil evaluasi dan kebutuhan analisis. Perbaikan model dapat dilakukan dengan mengubah spesifikasi model, menambahkan variabel baru, atau menggunakan metode estimasi yang berbeda.
Aplikasi Ekonometrika dalam Ekonomi
Ekonometrika merupakan alat yang sangat berguna dalam analisis data ekonomi. Ia menggabungkan teori ekonomi, statistik, dan matematika untuk membangun model-model kuantitatif yang dapat menjelaskan dan memprediksi fenomena ekonomi. Dengan menggunakan data historis, ekonometrika dapat membantu kita memahami hubungan antar variabel ekonomi dan mengevaluasi dampak kebijakan ekonomi.
Analisis Data Ekonomi Makro
Ekonometrika dapat digunakan untuk menganalisis data ekonomi makro, seperti pertumbuhan ekonomi, inflasi, dan pengangguran. Misalnya, ekonometrika dapat digunakan untuk menguji hubungan antara investasi dan pertumbuhan ekonomi. Model ekonometrika dapat menunjukkan bahwa investasi yang lebih tinggi berkorelasi positif dengan pertumbuhan ekonomi yang lebih tinggi. Model ini dapat digunakan untuk memprediksi pertumbuhan ekonomi di masa depan berdasarkan tingkat investasi saat ini.
Analisis Data Ekonomi Mikro
Ekonometrika juga dapat digunakan untuk menganalisis data ekonomi mikro, seperti permintaan konsumen, penawaran produk, dan perilaku investasi. Misalnya, ekonometrika dapat digunakan untuk menguji hubungan antara harga dan permintaan suatu produk. Model ekonometrika dapat menunjukkan bahwa permintaan untuk produk tersebut menurun seiring dengan kenaikan harga. Model ini dapat digunakan untuk memprediksi permintaan untuk produk tersebut di masa depan berdasarkan harga saat ini.
- Model ekonometrika dapat digunakan untuk menganalisis pengaruh faktor-faktor seperti pendapatan, harga barang substitusi, dan preferensi konsumen terhadap permintaan produk.
- Ekonometrika juga dapat digunakan untuk menganalisis perilaku perusahaan, seperti bagaimana mereka menentukan harga dan kuantitas produksi, dan bagaimana mereka merespon perubahan dalam kondisi pasar.
Aplikasi Ekonometrika dalam Isu Ekonomi Terkini
Ekonometrika juga dapat digunakan untuk menganalisis isu-isu ekonomi terkini, seperti dampak kebijakan fiskal terhadap pertumbuhan ekonomi. Misalnya, ekonometrika dapat digunakan untuk menguji hubungan antara pengeluaran pemerintah dan pertumbuhan ekonomi. Model ekonometrika dapat menunjukkan bahwa peningkatan pengeluaran pemerintah berkorelasi positif dengan pertumbuhan ekonomi yang lebih tinggi. Model ini dapat digunakan untuk memprediksi dampak kebijakan fiskal terhadap pertumbuhan ekonomi di masa depan.
- Ekonometrika dapat digunakan untuk menganalisis efektivitas program-program bantuan sosial terhadap pengangguran dan kemiskinan.
- Ekonometrika juga dapat digunakan untuk menganalisis dampak perubahan kebijakan moneter terhadap inflasi dan pertumbuhan ekonomi.
Contoh Soal Ekonometrika
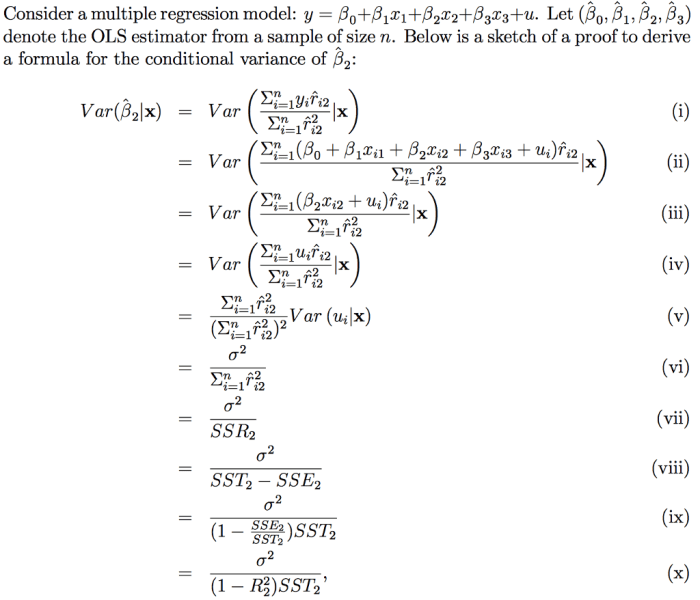
Ekonometrika adalah cabang ilmu ekonomi yang menggunakan metode statistik untuk menganalisis data ekonomi. Tujuannya adalah untuk menguji teori ekonomi, membuat prediksi, dan memberikan informasi untuk pengambilan keputusan. Dalam mempelajari ekonometrika, kita akan mempelajari berbagai model dan teknik analisis, salah satunya adalah analisis regresi. Regresi merupakan alat yang powerful untuk mempelajari hubungan antara variabel-variabel ekonomi.
Analisis Regresi Linier Sederhana
Analisis regresi linier sederhana merupakan teknik yang digunakan untuk mempelajari hubungan linear antara dua variabel, yaitu variabel dependen (Y) dan variabel independen (X). Model regresi linier sederhana dapat dituliskan sebagai berikut:
Y = β0 + β1X + ε
di mana:
- Y adalah variabel dependen
- X adalah variabel independen
- β0 adalah konstanta
- β1 adalah koefisien regresi
- ε adalah error term
Contoh soal ekonometrika yang membahas tentang analisis regresi linier sederhana:
Seorang peneliti ingin mempelajari hubungan antara jumlah jam belajar (X) dengan nilai ujian (Y) pada mahasiswa. Peneliti mengumpulkan data dari 50 mahasiswa dan mendapatkan hasil sebagai berikut:
| Mahasiswa | Jumlah Jam Belajar (X) | Nilai Ujian (Y) |
|---|---|---|
| 1 | 10 | 75 |
| 2 | 12 | 80 |
| … | … | … |
| 50 | 15 | 90 |
Peneliti ingin menguji apakah terdapat hubungan linear antara jumlah jam belajar dengan nilai ujian. Jika ya, peneliti ingin mengetahui berapa besar pengaruh jumlah jam belajar terhadap nilai ujian.
Analisis Regresi Linier Berganda
Analisis regresi linier berganda adalah teknik yang digunakan untuk mempelajari hubungan linear antara satu variabel dependen (Y) dengan dua atau lebih variabel independen (X1, X2, … , Xk). Model regresi linier berganda dapat dituliskan sebagai berikut:
Y = β0 + β1X1 + β2X2 + … + βkXk + ε
di mana:
- Y adalah variabel dependen
- X1, X2, … , Xk adalah variabel independen
- β0 adalah konstanta
- β1, β2, … , βk adalah koefisien regresi
- ε adalah error term
Contoh soal ekonometrika yang melibatkan analisis regresi linier berganda:
Seorang ekonom ingin mempelajari pengaruh inflasi (X1) dan suku bunga (X2) terhadap pertumbuhan ekonomi (Y). Ekonom mengumpulkan data dari 10 tahun terakhir dan mendapatkan hasil sebagai berikut:
| Tahun | Pertumbuhan Ekonomi (Y) | Inflasi (X1) | Suku Bunga (X2) |
|---|---|---|---|
| 2013 | 5.2 | 3.5 | 6.0 |
| 2014 | 4.8 | 4.0 | 5.5 |
| … | … | … | … |
| 2022 | 3.0 | 5.5 | 4.0 |
Ekonom ingin menguji apakah terdapat hubungan linear antara inflasi, suku bunga, dan pertumbuhan ekonomi. Jika ya, ekonom ingin mengetahui berapa besar pengaruh inflasi dan suku bunga terhadap pertumbuhan ekonomi.
Model Ekonometrika Non-Linier
Model ekonometrika non-linier adalah model yang melibatkan hubungan non-linear antara variabel dependen dan variabel independen. Model ini sering digunakan untuk menggambarkan hubungan yang lebih kompleks antara variabel-variabel ekonomi.
Contoh soal ekonometrika yang mengkaji tentang model ekonometrika non-linier:
Seorang analis pasar ingin mempelajari hubungan antara harga saham (Y) dengan pendapatan perusahaan (X). Analis menduga bahwa hubungan antara harga saham dan pendapatan perusahaan tidak linear, tetapi berbentuk kurva. Analis mengumpulkan data dari 20 perusahaan dan mendapatkan hasil sebagai berikut:
| Perusahaan | Harga Saham (Y) | Pendapatan Perusahaan (X) |
|---|---|---|
| 1 | 100 | 10 |
| 2 | 120 | 15 |
| … | … | … |
| 20 | 200 | 30 |
Analis ingin menguji apakah terdapat hubungan non-linear antara harga saham dan pendapatan perusahaan. Jika ya, analis ingin mengetahui bentuk kurva hubungan tersebut.
Teknik Estimasi dalam Ekonometrika
Ekonometrika merupakan cabang ilmu ekonomi yang menggabungkan teori ekonomi, matematika, dan statistika untuk menganalisis data ekonomi. Teknik estimasi memegang peranan penting dalam ekonometrika karena memungkinkan peneliti untuk menguji hipotesis dan mengukur hubungan antara variabel ekonomi. Ada berbagai teknik estimasi yang digunakan dalam ekonometrika, masing-masing dengan keunggulan dan kelemahannya sendiri.
Ordinary Least Squares (OLS)
OLS adalah teknik estimasi yang paling umum digunakan dalam ekonometrika. Teknik ini bertujuan untuk meminimalkan jumlah kuadrat kesalahan antara nilai variabel dependen yang diprediksi dan nilai variabel dependen yang sebenarnya. OLS merupakan teknik yang relatif mudah dipahami dan diterapkan, dan sering digunakan dalam model regresi linier.
Maximum Likelihood Estimation (MLE)
MLE adalah teknik estimasi yang bertujuan untuk menemukan nilai parameter model yang memaksimalkan kemungkinan data yang diamati. Teknik ini lebih kompleks daripada OLS, tetapi dapat memberikan estimasi yang lebih efisien jika asumsi model terpenuhi. MLE sering digunakan dalam model non-linier dan model dengan variabel dependen diskrit.
Generalized Method of Moments (GMM)
GMM adalah teknik estimasi yang lebih umum daripada OLS dan MLE. Teknik ini tidak bergantung pada asumsi distribusi variabel, sehingga dapat digunakan dalam berbagai model ekonometrika. GMM menggunakan persamaan momen untuk mengestimasi parameter model, dan dapat digunakan untuk mengestimasi model dengan variabel dependen diskrit, variabel laten, dan model dengan heteroskedastisitas.
Contoh Penerapan Teknik Estimasi
Misalkan kita ingin mempelajari pengaruh tingkat pengangguran terhadap inflasi. Kita dapat menggunakan model regresi linier sederhana dengan tingkat pengangguran sebagai variabel independen dan inflasi sebagai variabel dependen. Dengan menggunakan OLS, kita dapat mengestimasi koefisien regresi yang menunjukkan hubungan antara kedua variabel. Jika koefisien regresi signifikan secara statistik, maka kita dapat menyimpulkan bahwa tingkat pengangguran memiliki pengaruh signifikan terhadap inflasi.
Tabel Teknik Estimasi
| Teknik Estimasi | Keunggulan | Kelemahan | Contoh Penerapan |
|---|---|---|---|
| OLS | Relatif mudah dipahami dan diterapkan | Asumsi model harus terpenuhi | Model regresi linier sederhana |
| MLE | Estimasi yang lebih efisien jika asumsi model terpenuhi | Lebih kompleks daripada OLS | Model non-linier dan model dengan variabel dependen diskrit |
| GMM | Lebih umum daripada OLS dan MLE | Membutuhkan persamaan momen yang tepat | Model dengan variabel dependen diskrit, variabel laten, dan model dengan heteroskedastisitas |
Pengujian Hipotesis dalam Ekonometrika
Pengujian hipotesis merupakan bagian penting dalam ekonometrika. Melalui pengujian hipotesis, kita dapat menguji dan memvalidasi model ekonometrika yang telah kita bangun. Tujuannya adalah untuk melihat apakah model tersebut sesuai dengan data yang ada dan apakah dapat digunakan untuk memprediksi atau menjelaskan fenomena ekonomi yang sedang diteliti.
Jenis-Jenis Pengujian Hipotesis
Dalam ekonometrika, terdapat berbagai jenis pengujian hipotesis yang umum digunakan. Beberapa jenis pengujian yang paling umum meliputi:
- t-test: Pengujian t-test digunakan untuk menguji hipotesis tentang nilai parameter tunggal dalam model ekonometrika. Misalnya, kita dapat menggunakan t-test untuk menguji apakah koefisien regresi suatu variabel independen signifikan secara statistik atau tidak.
- F-test: Pengujian F-test digunakan untuk menguji hipotesis tentang beberapa parameter dalam model ekonometrika. Misalnya, kita dapat menggunakan F-test untuk menguji apakah model regresi secara keseluruhan signifikan secara statistik atau tidak.
- Chi-square test: Pengujian chi-square test digunakan untuk menguji hipotesis tentang hubungan antara variabel kategorikal. Misalnya, kita dapat menggunakan chi-square test untuk menguji apakah ada hubungan signifikan antara jenis kelamin dan preferensi konsumen terhadap produk tertentu.
Contoh Soal Ekonometrika
Misalnya, kita ingin menguji apakah ada hubungan signifikan antara jumlah tahun pendidikan (X) dan pendapatan (Y) seseorang. Kita dapat membangun model regresi linier sederhana sebagai berikut:
Y = β0 + β1X + ε
Hipotesis nol (H0) adalah tidak ada hubungan signifikan antara pendidikan dan pendapatan, atau β1 = 0. Hipotesis alternatif (H1) adalah ada hubungan signifikan antara pendidikan dan pendapatan, atau β1 ≠ 0. Kita dapat menggunakan t-test untuk menguji hipotesis ini.
Tabel Rangkuman Pengujian Hipotesis
| Jenis Pengujian | Tujuan | Prosedur | Contoh Penerapan |
|---|---|---|---|
| t-test | Menguji hipotesis tentang nilai parameter tunggal | Menghitung statistik t dan membandingkannya dengan nilai kritis | Menguji apakah koefisien regresi suatu variabel independen signifikan secara statistik atau tidak |
| F-test | Menguji hipotesis tentang beberapa parameter | Menghitung statistik F dan membandingkannya dengan nilai kritis | Menguji apakah model regresi secara keseluruhan signifikan secara statistik atau tidak |
| Chi-square test | Menguji hipotesis tentang hubungan antara variabel kategorikal | Menghitung statistik chi-square dan membandingkannya dengan nilai kritis | Menguji apakah ada hubungan signifikan antara jenis kelamin dan preferensi konsumen terhadap produk tertentu |
Permasalahan dalam Ekonometrika
Ekonometrika, sebagai cabang ilmu yang menggabungkan teori ekonomi, matematika, dan statistika, berperan penting dalam menganalisis data ekonomi dan menguji hipotesis ekonomi. Namun, dalam praktiknya, analisis ekonometrika tidak selalu berjalan mulus. Terdapat beberapa permasalahan yang mungkin dihadapi, yang jika tidak ditangani dengan tepat, dapat memengaruhi validitas dan reliabilitas hasil analisis.
Multikolinearitas
Multikolinearitas terjadi ketika dua atau lebih variabel independen dalam model regresi memiliki hubungan linear yang kuat. Kondisi ini membuat sulit untuk mengidentifikasi secara pasti pengaruh masing-masing variabel independen terhadap variabel dependen. Hal ini karena variabel independen saling “bercampur” sehingga sulit untuk memisahkan efek individualnya.
- Penyebab: Korelasi tinggi antara variabel independen, penggunaan data yang sama dalam model, dan adanya variabel “dummy” yang berlebihan.
- Gejala: Koefisien regresi yang tidak stabil dan sensitif terhadap perubahan kecil dalam data, nilai p-value yang tinggi untuk koefisien, dan nilai R-squared yang tinggi namun koefisien regresi yang tidak signifikan.
- Solusi: Menghilangkan variabel yang berkorelasi tinggi, menggunakan model regresi yang lebih sederhana, atau menggunakan teknik regresi ridge atau lasso untuk mengatasi multikolinearitas.
Heteroskedastisitas
Heteroskedastisitas terjadi ketika varians residual dalam model regresi tidak konstan. Kondisi ini berarti bahwa penyebaran kesalahan prediksi tidak sama untuk semua nilai variabel independen. Heteroskedastisitas dapat menyebabkan kesalahan dalam estimasi koefisien regresi dan uji hipotesis.
- Penyebab: Data yang tidak homogen, kesalahan pengukuran yang berbeda, dan pengaruh variabel independen yang berbeda terhadap varians residual.
- Gejala: Residual yang memiliki pola tertentu, seperti penyebaran yang semakin besar untuk nilai variabel independen yang lebih tinggi. Uji statistik seperti uji White atau uji Breusch-Pagan dapat digunakan untuk mendeteksi heteroskedastisitas.
- Solusi: Menggunakan model regresi yang memperhitungkan heteroskedastisitas, seperti model regresi dengan varians yang tidak konstan, atau menggunakan transformasi data untuk menstabilkan varians residual.
Autokorelasi
Autokorelasi terjadi ketika residual dalam model regresi berkorelasi dengan residual sebelumnya. Kondisi ini sering terjadi dalam data time series, di mana pengamatan yang berdekatan dalam waktu cenderung memiliki korelasi. Autokorelasi dapat menyebabkan estimasi koefisien regresi yang bias dan uji hipotesis yang tidak valid.
- Penyebab: Data time series yang tidak stasioner, adanya tren atau siklus dalam data, dan model regresi yang tidak tepat.
- Gejala: Residual yang menunjukkan pola tertentu, seperti pola bergelombang atau pola yang terkonsentrasi di atas atau di bawah garis nol. Uji statistik seperti uji Durbin-Watson dapat digunakan untuk mendeteksi autokorelasi.
- Solusi: Menggunakan model regresi yang memperhitungkan autokorelasi, seperti model autoregresif (AR) atau model moving average (MA), atau menggunakan teknik regresi yang robust terhadap autokorelasi.
| Permasalahan | Penyebab | Gejala | Solusi |
|---|---|---|---|
| Multikolinearitas | Korelasi tinggi antara variabel independen, penggunaan data yang sama dalam model, dan adanya variabel “dummy” yang berlebihan. | Koefisien regresi yang tidak stabil dan sensitif terhadap perubahan kecil dalam data, nilai p-value yang tinggi untuk koefisien, dan nilai R-squared yang tinggi namun koefisien regresi yang tidak signifikan. | Menghilangkan variabel yang berkorelasi tinggi, menggunakan model regresi yang lebih sederhana, atau menggunakan teknik regresi ridge atau lasso untuk mengatasi multikolinearitas. |
| Heteroskedastisitas | Data yang tidak homogen, kesalahan pengukuran yang berbeda, dan pengaruh variabel independen yang berbeda terhadap varians residual. | Residual yang memiliki pola tertentu, seperti penyebaran yang semakin besar untuk nilai variabel independen yang lebih tinggi. Uji statistik seperti uji White atau uji Breusch-Pagan dapat digunakan untuk mendeteksi heteroskedastisitas. | Menggunakan model regresi yang memperhitungkan heteroskedastisitas, seperti model regresi dengan varians yang tidak konstan, atau menggunakan transformasi data untuk menstabilkan varians residual. |
| Autokorelasi | Data time series yang tidak stasioner, adanya tren atau siklus dalam data, dan model regresi yang tidak tepat. | Residual yang menunjukkan pola tertentu, seperti pola bergelombang atau pola yang terkonsentrasi di atas atau di bawah garis nol. Uji statistik seperti uji Durbin-Watson dapat digunakan untuk mendeteksi autokorelasi. | Menggunakan model regresi yang memperhitungkan autokorelasi, seperti model autoregresif (AR) atau model moving average (MA), atau menggunakan teknik regresi yang robust terhadap autokorelasi. |
Software Ekonometrika: Contoh Soal Ekonometrika
Analisis ekonometrika membutuhkan software khusus untuk mengolah data dan menjalankan model statistik. Berbagai software ekonometrika tersedia, masing-masing dengan keunggulan dan kekurangannya sendiri.
Software Ekonometrika yang Umum Digunakan
Beberapa software ekonometrika yang umum digunakan dalam analisis ekonomi adalah:
- Eviews: Eviews (Econometric Views) merupakan software ekonometrika yang populer dan mudah digunakan. Eviews menyediakan antarmuka grafis yang intuitif dan berbagai fitur untuk analisis ekonometrika, seperti regresi linier, regresi non-linier, model VAR, dan model ARCH/GARCH.
- Stata: Stata adalah software statistik yang kuat dan fleksibel yang juga banyak digunakan dalam ekonometrika. Stata memiliki sintaks pemrograman yang mudah dipelajari dan menawarkan berbagai macam perintah dan paket untuk analisis ekonometrika, termasuk analisis data panel, model probit, dan model logit.
- R: R adalah bahasa pemrograman dan lingkungan statistik yang open source dan gratis. R sangat populer di kalangan akademisi dan peneliti karena fleksibilitas dan kemampuannya untuk melakukan analisis ekonometrika yang canggih. R memiliki berbagai paket yang dapat digunakan untuk analisis ekonometrika, seperti “plm” untuk analisis data panel, “glmnet” untuk regresi lasso, dan “vars” untuk model VAR.
Keunggulan dan Kekurangan Software Ekonometrika
Setiap software ekonometrika memiliki keunggulan dan kekurangannya sendiri. Berikut adalah beberapa perbandingan:
| Software | Keunggulan | Kekurangan |
|---|---|---|
| Eviews | Antarmuka grafis yang mudah digunakan, fitur lengkap untuk analisis ekonometrika, harga yang relatif terjangkau. | Fleksibilitas yang terbatas, tidak sekuat Stata atau R dalam hal pemrograman dan kemampuan analisis. |
| Stata | Sintaks pemrograman yang mudah dipelajari, berbagai macam perintah dan paket, kemampuan analisis yang kuat. | Harga yang relatif mahal, antarmuka grafis yang kurang intuitif dibandingkan Eviews. |
| R | Open source dan gratis, fleksibilitas yang tinggi, berbagai macam paket untuk analisis ekonometrika. | Kurva belajar yang lebih curam, antarmuka grafis yang kurang user-friendly. |
Contoh Demonstrasi Penggunaan Eviews
Misalkan kita ingin menganalisis hubungan antara inflasi dan pertumbuhan ekonomi. Kita dapat menggunakan Eviews untuk melakukan analisis regresi linier.
Pertama, kita perlu mengimpor data inflasi dan pertumbuhan ekonomi ke dalam Eviews. Setelah data diimpor, kita dapat menjalankan regresi linier dengan memasukkan inflasi sebagai variabel independen dan pertumbuhan ekonomi sebagai variabel dependen. Eviews akan menghasilkan output yang berisi koefisien regresi, nilai p, dan statistik lainnya yang dapat digunakan untuk menginterpretasikan hasil regresi.
Contohnya, jika kita menemukan bahwa koefisien regresi inflasi signifikan dan negatif, maka hal ini menunjukkan bahwa inflasi memiliki efek negatif yang signifikan terhadap pertumbuhan ekonomi.
Terakhir
Ekonometrika, dengan kemampuannya untuk menggabungkan teori ekonomi dengan metode statistik, memberikan alat yang ampuh untuk memahami data ekonomi dan membuat keputusan yang lebih baik. Melalui contoh-contoh soal yang telah dibahas, Anda dapat melihat bagaimana ekonometrika dapat digunakan untuk menganalisis hubungan antara variabel ekonomi, menguji hipotesis, dan membuat prediksi.




