Contoh soal fpb kpk – Pernahkah Anda mendengar istilah FPB dan KPK? Kedua istilah ini merupakan konsep dasar dalam matematika yang sering kita jumpai dalam kehidupan sehari-hari. FPB, singkatan dari Faktor Persekutuan Terbesar, adalah bilangan terbesar yang dapat membagi habis dua bilangan atau lebih. Sedangkan KPK, singkatan dari Kelipatan Persekutuan Terkecil, adalah bilangan terkecil yang merupakan kelipatan persekutuan dari dua bilangan atau lebih.
Memahami FPB dan KPK tidak hanya penting untuk menyelesaikan soal matematika di sekolah, tetapi juga untuk menyelesaikan berbagai masalah dalam kehidupan nyata. Misalnya, ketika membagi kue kepada beberapa anak dengan jumlah yang sama, kita perlu mencari FPB untuk menentukan ukuran potongan kue yang paling besar. Atau, ketika ingin mengatur jadwal kegiatan yang melibatkan beberapa orang, kita perlu mencari KPK untuk menentukan waktu pertemuan yang paling cepat.
Pengertian FPB dan KPK
Dalam matematika, FPB dan KPK adalah konsep penting yang digunakan untuk menyelesaikan berbagai masalah, terutama yang berkaitan dengan pembagian dan penggabungan. FPB (Faktor Persekutuan Terbesar) dan KPK (Kelipatan Persekutuan Terkecil) merupakan dua konsep yang saling berhubungan dan memiliki aplikasi luas dalam kehidupan sehari-hari.
Faktor Persekutuan Terbesar (FPB), Contoh soal fpb kpk
FPB dari dua bilangan atau lebih adalah bilangan bulat positif terbesar yang merupakan faktor dari semua bilangan tersebut. Dengan kata lain, FPB adalah bilangan terbesar yang dapat membagi habis semua bilangan yang diberikan tanpa meninggalkan sisa.
Kelipatan Persekutuan Terkecil (KPK)
KPK dari dua bilangan atau lebih adalah bilangan bulat positif terkecil yang merupakan kelipatan dari semua bilangan tersebut. Dengan kata lain, KPK adalah bilangan terkecil yang dapat dibagi habis oleh semua bilangan yang diberikan.
Perbandingan FPB dan KPK
| Konsep | FPB | KPK |
|---|---|---|
| Definisi | Bilangan bulat positif terbesar yang merupakan faktor dari semua bilangan yang diberikan. | Bilangan bulat positif terkecil yang merupakan kelipatan dari semua bilangan yang diberikan. |
| Cara Mencari |
|
|
| Contoh | FPB dari 12 dan 18 adalah 6. Faktorisasi prima dari 12 adalah 22 x 3 dan faktorisasi prima dari 18 adalah 2 x 32. FPB adalah 2 x 3 = 6. | KPK dari 12 dan 18 adalah 36. Faktorisasi prima dari 12 adalah 22 x 3 dan faktorisasi prima dari 18 adalah 2 x 32. KPK adalah 22 x 32 = 36. |
Soal Latihan FPB dan KPK
Setelah memahami konsep FPB dan KPK, saatnya kita berlatih! Berikut adalah beberapa soal latihan FPB dan KPK dengan tingkat kesulitan yang berbeda. Selesaikan soal-soal ini untuk menguji pemahamanmu tentang FPB dan KPK. Jangan lupa untuk melihat kunci jawaban di akhir untuk memastikan jawabanmu benar.
Soal Latihan FPB
Berikut adalah lima soal latihan FPB dengan tingkat kesulitan yang berbeda.
- Tentukan FPB dari 12 dan 18.
- Tentukan FPB dari 24, 36, dan 48.
- Tentukan FPB dari 100 dan 150.
- Tentukan FPB dari 252 dan 378.
- Tentukan FPB dari 1.000 dan 1.500.
Soal Latihan KPK
Berikut adalah lima soal latihan KPK dengan tingkat kesulitan yang berbeda.
- Tentukan KPK dari 4 dan 6.
- Tentukan KPK dari 8, 12, dan 16.
- Tentukan KPK dari 20 dan 30.
- Tentukan KPK dari 120 dan 180.
- Tentukan KPK dari 250 dan 375.
Kunci Jawaban
Berikut adalah kunci jawaban untuk soal latihan FPB dan KPK di atas.
| Soal | Kunci Jawaban |
|---|---|
| FPB dari 12 dan 18 | 6 |
| FPB dari 24, 36, dan 48 | 12 |
| FPB dari 100 dan 150 | 50 |
| FPB dari 252 dan 378 | 126 |
| FPB dari 1.000 dan 1.500 | 500 |
| KPK dari 4 dan 6 | 12 |
| KPK dari 8, 12, dan 16 | 48 |
| KPK dari 20 dan 30 | 60 |
| KPK dari 120 dan 180 | 360 |
| KPK dari 250 dan 375 | 750 |
Tips dan Trik Mencari FPB dan KPK
Mencari FPB dan KPK mungkin terdengar rumit, tapi sebenarnya ada beberapa tips dan trik yang bisa kamu gunakan untuk mempermudah prosesnya. Dengan memahami beberapa teknik dasar, kamu bisa menemukan FPB dan KPK dengan cepat dan mudah, bahkan untuk angka yang besar sekalipun.
Mencari FPB
FPB (Faktor Persekutuan Terbesar) adalah faktor terbesar yang sama dari dua atau lebih bilangan. Berikut beberapa tips untuk menemukan FPB dengan mudah:
- Metode Faktorisasi Prima: Metode ini melibatkan penguraian setiap bilangan menjadi faktor primanya. Setelah itu, cari faktor prima yang sama dari semua bilangan dan kalikan faktor-faktor tersebut. Hasilnya adalah FPB dari bilangan-bilangan tersebut. Misalnya, FPB dari 12 dan 18 adalah 6, karena faktor prima dari 12 adalah 2 x 2 x 3 dan faktor prima dari 18 adalah 2 x 3 x 3. Faktor prima yang sama adalah 2 dan 3, sehingga FPB-nya adalah 2 x 3 = 6.
- Metode Bagi Panjang: Metode ini melibatkan pembagian setiap bilangan dengan faktor persekutuan terkecil. Ulangi proses ini hingga tidak ada lagi faktor persekutuan yang sama. Faktor terakhir yang digunakan untuk membagi adalah FPB dari bilangan-bilangan tersebut. Misalnya, untuk mencari FPB dari 24 dan 36, kita bisa membagi keduanya dengan 2, kemudian dengan 2 lagi, dan terakhir dengan 3. Karena 3 adalah faktor terakhir yang digunakan untuk membagi, maka FPB dari 24 dan 36 adalah 3.
- Metode Faktor Persekutuan: Metode ini melibatkan pencarian semua faktor dari setiap bilangan. Kemudian, cari faktor persekutuan terbesar dari semua bilangan. Misalnya, faktor dari 12 adalah 1, 2, 3, 4, 6, dan 12, sedangkan faktor dari 18 adalah 1, 2, 3, 6, 9, dan 18. Faktor persekutuan terbesar dari 12 dan 18 adalah 6.
Mencari KPK
KPK (Kelipatan Persekutuan Terkecil) adalah kelipatan terkecil yang sama dari dua atau lebih bilangan. Berikut beberapa tips untuk menemukan KPK dengan mudah:
- Metode Kelipatan: Metode ini melibatkan pencarian kelipatan dari bilangan terbesar hingga menemukan kelipatan yang sama dengan bilangan lainnya. Misalnya, KPK dari 4 dan 6 adalah 12, karena 12 adalah kelipatan terkecil yang sama dari 4 dan 6.
- Metode Faktorisasi Prima: Metode ini melibatkan penguraian setiap bilangan menjadi faktor primanya. Setelah itu, cari faktor prima yang sama dan berbeda dari semua bilangan dan kalikan faktor-faktor tersebut. Hasilnya adalah KPK dari bilangan-bilangan tersebut. Misalnya, KPK dari 12 dan 18 adalah 36, karena faktor prima dari 12 adalah 2 x 2 x 3 dan faktor prima dari 18 adalah 2 x 3 x 3. Faktor prima yang sama adalah 2 dan 3, sedangkan faktor prima yang berbeda adalah 2 dan 3. Maka, KPK-nya adalah 2 x 2 x 3 x 3 = 36.
- Metode FPB: Metode ini melibatkan penggunaan FPB untuk mencari KPK. Rumusnya adalah: KPK (a, b) = (a x b) / FPB (a, b). Misalnya, KPK dari 12 dan 18 adalah 36, karena FPB dari 12 dan 18 adalah 6. Maka, KPK (12, 18) = (12 x 18) / 6 = 36.
Soal Cerita FPB dan KPK
Soal cerita FPB dan KPK adalah soal yang memadukan konsep matematika dengan situasi sehari-hari. Soal ini biasanya disajikan dalam bentuk cerita yang mengharuskan kita untuk memahami dan menerapkan konsep FPB dan KPK untuk menemukan solusi. Melalui soal cerita, kita dapat melihat bagaimana FPB dan KPK berperan dalam kehidupan nyata.
Soal Cerita FPB
Soal cerita FPB biasanya melibatkan konsep pembagian atau pengelompokan. Berikut contohnya:
- Budi memiliki 24 buah apel dan 36 buah jeruk. Budi ingin membagi apel dan jeruk tersebut ke dalam beberapa keranjang dengan jumlah apel dan jeruk yang sama di setiap keranjang. Berapakah jumlah keranjang terbanyak yang dapat dibuat Budi?
Untuk menyelesaikan soal cerita FPB, kita perlu mencari faktor persekutuan terbesar (FPB) dari 24 dan 36. FPB dari 24 dan 36 adalah 12. Ini berarti Budi dapat membuat 12 keranjang dengan jumlah apel dan jeruk yang sama di setiap keranjang.
Soal Cerita KPK
Soal cerita KPK biasanya melibatkan konsep pengaturan jadwal atau pembelian barang. Berikut contohnya:
- Rina dan Roni berlatih renang di kolam renang yang sama. Rina berlatih setiap 3 hari sekali, sedangkan Roni berlatih setiap 4 hari sekali. Jika mereka berlatih bersama pada hari Senin, pada hari apa mereka akan berlatih bersama lagi?
Untuk menyelesaikan soal cerita KPK, kita perlu mencari kelipatan persekutuan terkecil (KPK) dari 3 dan 4. KPK dari 3 dan 4 adalah 12. Ini berarti Rina dan Roni akan berlatih bersama lagi setelah 12 hari, yaitu pada hari Sabtu.
Ilustrasi Gambar Soal Cerita FPB dan KPK
Untuk memperjelas pemahaman, berikut ilustrasi gambar untuk soal cerita FPB dan KPK:
Ilustrasi Gambar Soal Cerita FPB
Contoh soal FPB dan KPK memang sering ditemui dalam pelajaran matematika. Kamu bisa menemukan contoh soal FPB dan KPK di buku pelajaran, website, atau bahkan aplikasi belajar online. Nah, kalau kamu sedang belajar tentang sebab akibat dalam bahasa Inggris, kamu bisa cek contoh soal “because” dan “because of” di contoh soal because dan because of.
Dengan memahami konsep “because” dan “because of”, kamu bisa lebih mudah memahami dan menyelesaikan soal FPB dan KPK yang melibatkan kalimat-kalimat yang menjelaskan hubungan sebab akibat.
Gambar tersebut menunjukkan 24 buah apel dan 36 buah jeruk yang akan dibagi ke dalam beberapa keranjang. Setiap keranjang berisi jumlah apel dan jeruk yang sama. Gambar tersebut menunjukkan bahwa FPB dari 24 dan 36 adalah 12, sehingga Budi dapat membuat 12 keranjang dengan jumlah apel dan jeruk yang sama di setiap keranjang.
Ilustrasi Gambar Soal Cerita KPK
Gambar tersebut menunjukkan jadwal latihan renang Rina dan Roni. Rina berlatih setiap 3 hari sekali, sedangkan Roni berlatih setiap 4 hari sekali. Gambar tersebut menunjukkan bahwa KPK dari 3 dan 4 adalah 12, sehingga Rina dan Roni akan berlatih bersama lagi setelah 12 hari, yaitu pada hari Sabtu.
Pembahasan Soal FPB dan KPK
Setelah mempelajari konsep FPB dan KPK, mari kita bahas beberapa contoh soal untuk menguji pemahamanmu. Kali ini, kita akan membahas dua soal latihan yang telah disiapkan sebelumnya. Tujuannya adalah untuk menunjukkan langkah-langkah penyelesaian soal FPB dan KPK secara sistematis.
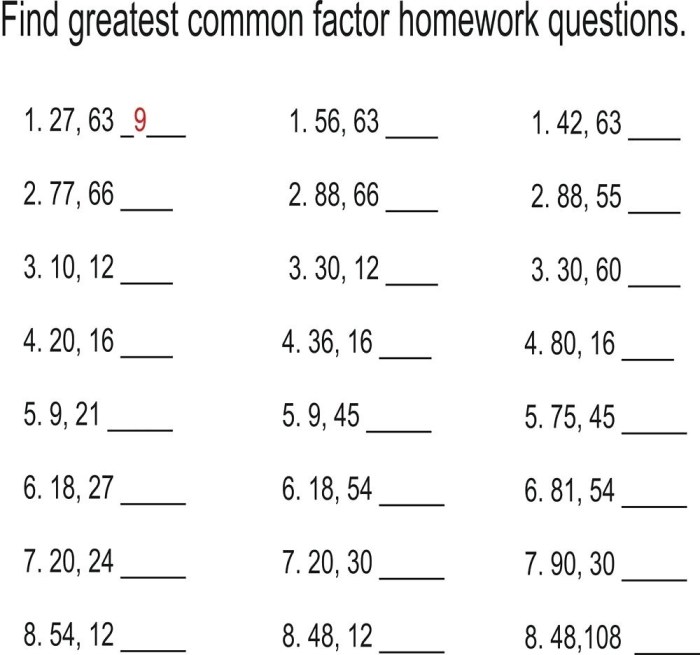
Soal 1: Mencari FPB dari 12, 18, dan 24
Soal ini mengharuskan kita untuk mencari faktor persekutuan terbesar (FPB) dari tiga bilangan, yaitu 12, 18, dan 24. Untuk menemukan FPB, kita perlu mengidentifikasi faktor-faktor dari setiap bilangan tersebut dan kemudian mencari faktor persekutuan terbesarnya.
Berikut langkah-langkah mencari FPB dari 12, 18, dan 24:
- Cari faktor dari 12: 1, 2, 3, 4, 6, dan 12.
- Cari faktor dari 18: 1, 2, 3, 6, 9, dan 18.
- Cari faktor dari 24: 1, 2, 3, 4, 6, 8, 12, dan 24.
- Identifikasi faktor persekutuan dari ketiga bilangan tersebut: 1, 2, 3, dan 6.
- Faktor persekutuan terbesar (FPB) dari 12, 18, dan 24 adalah 6.
Soal 2: Mencari KPK dari 15 dan 20
Soal ini mengharuskan kita untuk mencari kelipatan persekutuan terkecil (KPK) dari dua bilangan, yaitu 15 dan 20. Untuk menemukan KPK, kita perlu mengidentifikasi kelipatan dari setiap bilangan tersebut dan kemudian mencari kelipatan persekutuan terkecilnya.
Berikut langkah-langkah mencari KPK dari 15 dan 20:
- Cari kelipatan dari 15: 15, 30, 45, 60, 75, 90, …
- Cari kelipatan dari 20: 20, 40, 60, 80, 100, …
- Identifikasi kelipatan persekutuan dari kedua bilangan tersebut: 60, 120, 180, …
- Kelipatan persekutuan terkecil (KPK) dari 15 dan 20 adalah 60.
Variasi Soal FPB dan KPK: Contoh Soal Fpb Kpk
Selain mencari FPB dan KPK dari dua atau lebih bilangan, kita juga bisa menemukan variasi soal yang melibatkan operasi penjumlahan, pengurangan, perkalian, dan pembagian. Mari kita bahas satu per satu!
Soal FPB yang Melibatkan Operasi Penjumlahan, Pengurangan, Perkalian, dan Pembagian
Soal FPB yang melibatkan operasi penjumlahan, pengurangan, perkalian, dan pembagian biasanya meminta kita untuk mencari FPB dari hasil operasi tersebut. Contohnya, “Tentukan FPB dari hasil penjumlahan 12 dan 18”.
- Langkah 1: Hitung hasil operasi yang diminta. Dalam contoh ini, hasil penjumlahan 12 dan 18 adalah 30.
- Langkah 2: Cari FPB dari hasil operasi tersebut. FPB dari 30 adalah 1, 2, 3, 5, 6, 10, 15, dan 30. FPB terbesar dari 30 adalah 30.
Soal KPK yang Melibatkan Operasi Penjumlahan, Pengurangan, Perkalian, dan Pembagian
Soal KPK yang melibatkan operasi penjumlahan, pengurangan, perkalian, dan pembagian juga meminta kita untuk mencari KPK dari hasil operasi tersebut. Contohnya, “Tentukan KPK dari hasil perkalian 4 dan 6”.
- Langkah 1: Hitung hasil operasi yang diminta. Dalam contoh ini, hasil perkalian 4 dan 6 adalah 24.
- Langkah 2: Cari KPK dari hasil operasi tersebut. KPK dari 24 adalah 1, 2, 3, 4, 6, 8, 12, dan 24. KPK terkecil dari 24 adalah 24.
Contoh Soal Variasi FPB dan KPK
Berikut adalah contoh soal variasi FPB dan KPK yang melibatkan operasi penjumlahan, pengurangan, perkalian, dan pembagian:
| No | Soal | Penyelesaian |
|---|---|---|
| 1 | Tentukan FPB dari hasil penjumlahan 15 dan 25. | 15 + 25 = 40. FPB dari 40 adalah 1, 2, 4, 5, 8, 10, 20, dan 40. FPB terbesar dari 40 adalah 40. |
| 2 | Tentukan KPK dari hasil pengurangan 24 dan 12. | 24 – 12 = 12. KPK dari 12 adalah 1, 2, 3, 4, 6, dan 12. KPK terkecil dari 12 adalah 12. |
| 3 | Tentukan FPB dari hasil perkalian 3 dan 7. | 3 x 7 = 21. FPB dari 21 adalah 1, 3, 7, dan 21. FPB terbesar dari 21 adalah 21. |
| 4 | Tentukan KPK dari hasil pembagian 36 dan 6. | 36 / 6 = 6. KPK dari 6 adalah 1, 2, 3, dan 6. KPK terkecil dari 6 adalah 6. |
Tips Menyelesaikan Soal Variasi FPB dan KPK
- Perhatikan operasi yang diminta dalam soal. Apakah penjumlahan, pengurangan, perkalian, atau pembagian?
- Hitung hasil operasi tersebut.
- Cari FPB atau KPK dari hasil operasi tersebut.
Akhir Kata
Dalam mempelajari FPB dan KPK, kita tidak hanya diajak untuk memahami konsep matematika, tetapi juga untuk mengembangkan kemampuan berpikir logis dan memecahkan masalah. Dengan memahami konsep ini, kita dapat lebih mudah menyelesaikan berbagai permasalahan dalam kehidupan sehari-hari, baik itu dalam hal membagi kue, mengatur jadwal, atau bahkan dalam bidang pekerjaan.