Contoh soal kedudukan titik garis dan bidang dalam ruang – Pernahkah kamu membayangkan bagaimana posisi sebuah titik, garis, dan bidang dalam ruang tiga dimensi? Konsep ini ternyata sangat penting dalam berbagai bidang, mulai dari arsitektur, teknik, hingga seni. Bayangkan, bagaimana seorang arsitek merancang sebuah bangunan tanpa memahami posisi dinding, atap, dan jendela? Atau bagaimana seorang seniman melukis sebuah objek tiga dimensi tanpa memahami perspektif dan penempatan objek dalam ruang?
Dalam artikel ini, kita akan menjelajahi konsep kedudukan titik, garis, dan bidang dalam ruang. Kita akan membahas berbagai kemungkinan posisi relatif antara titik, garis, dan bidang, serta mempelajari rumus untuk menghitung jarak antara mereka. Dengan memahami konsep ini, kita akan mendapatkan pemahaman yang lebih mendalam tentang dunia tiga dimensi yang kita tinggali.
Pengertian Titik, Garis, dan Bidang dalam Ruang
Dalam geometri ruang, titik, garis, dan bidang merupakan konsep dasar yang menjadi pondasi untuk mempelajari bentuk dan posisi objek di ruang tiga dimensi. Ketiga konsep ini saling berhubungan dan membentuk dasar untuk memahami bangun ruang seperti kubus, balok, limas, dan lainnya.
Pengertian Titik dalam Ruang
Titik dalam ruang adalah lokasi yang memiliki posisi tertentu dalam ruang tiga dimensi. Titik tidak memiliki dimensi, artinya tidak memiliki panjang, lebar, atau tinggi. Titik biasanya dilambangkan dengan huruf kapital, seperti A, B, C, dan seterusnya.
- Contoh titik dalam kehidupan sehari-hari: ujung pensil, ujung jarum, pusat lingkaran.
Pengertian Garis dalam Ruang
Garis dalam ruang adalah kumpulan titik-titik yang terhubung secara linear dan tak terhingga. Garis memiliki satu dimensi, yaitu panjang, dan tidak memiliki lebar atau tinggi. Garis dapat didefinisikan dengan dua titik yang berbeda, atau dengan persamaan linear.
- Contoh garis dalam kehidupan sehari-hari: tepi meja, kabel listrik, sinar matahari.
Pengertian Bidang dalam Ruang
Bidang dalam ruang adalah kumpulan titik-titik yang terhubung secara datar dan tak terhingga. Bidang memiliki dua dimensi, yaitu panjang dan lebar, dan tidak memiliki tinggi. Bidang dapat didefinisikan dengan tiga titik yang tidak segaris, atau dengan persamaan linear.
- Contoh bidang dalam kehidupan sehari-hari: permukaan meja, dinding ruangan, permukaan air danau.
Perbedaan Titik, Garis, dan Bidang dalam Ruang
| Konsep | Dimensi | Contoh |
|---|---|---|
| Titik | 0 | Ujung pensil |
| Garis | 1 | Tepi meja |
| Bidang | 2 | Permukaan meja |
Kedudukan Titik terhadap Garis
Dalam geometri ruang, titik dan garis merupakan dua konsep dasar yang saling berhubungan. Kedudukan titik terhadap garis merujuk pada posisi relatif titik tersebut terhadap garis. Titik dapat berada pada garis, di luar garis, atau bahkan tepat di atas garis. Mari kita bahas berbagai kemungkinan kedudukan titik terhadap garis dengan lebih detail.
Contoh soal kedudukan titik, garis, dan bidang dalam ruang bisa dibilang cukup menantang, karena melibatkan visualisasi tiga dimensi. Ingat, memahami konsep dasar seperti jarak, sudut, dan posisi relatif sangat penting untuk menyelesaikannya. Nah, untuk mengasah kemampuan dalam menganalisis soal-soal semacam ini, kamu bisa melatih diri dengan mengerjakan contoh soal artikel yang membahas materi serupa.
Salah satu sumber yang bisa kamu kunjungi adalah contoh soal artikel ini. Melalui contoh soal yang beragam, kamu akan semakin memahami bagaimana mengaplikasikan konsep geometri ruang dalam menyelesaikan masalah yang lebih kompleks.
Kedudukan Titik terhadap Garis
Ada tiga kemungkinan kedudukan titik terhadap garis, yaitu:
- Titik terletak pada garis: Titik ini berada tepat di atas garis, sehingga titik tersebut merupakan bagian dari garis itu sendiri. Ilustrasi: Titik A pada garis g.
- Titik terletak di luar garis: Titik ini tidak berada di atas garis, sehingga jarak antara titik dan garis lebih dari nol. Ilustrasi: Titik B di luar garis g.
- Titik terletak di atas garis: Titik ini tidak berada pada garis, tetapi juga tidak berada di luar garis. Ilustrasi: Titik C tepat di atas garis g.
Tabel Kedudukan Titik terhadap Garis
| Kedudukan | Ilustrasi | Contoh |
|---|---|---|
| Titik terletak pada garis | Titik A pada garis g | Titik A (2, 3, 1) terletak pada garis g dengan persamaan x = 2 + t, y = 3 + 2t, z = 1 + 3t. |
| Titik terletak di luar garis | Titik B di luar garis g | Titik B (1, 2, 3) terletak di luar garis g dengan persamaan x = 2 + t, y = 3 + 2t, z = 1 + 3t. |
| Titik terletak di atas garis | Titik C tepat di atas garis g | Titik C (2, 3, 2) terletak di atas garis g dengan persamaan x = 2 + t, y = 3 + 2t, z = 1 + 3t. |
Kedudukan Titik terhadap Bidang
Setelah memahami kedudukan titik terhadap garis, mari kita lanjutkan dengan membahas kedudukan titik terhadap bidang. Dalam geometri ruang, titik dapat memiliki berbagai posisi relatif terhadap suatu bidang. Pemahaman ini sangat penting dalam mempelajari konsep-konsep geometri ruang yang lebih kompleks seperti jarak, sudut, dan volume.
Kemungkinan Kedudukan Titik terhadap Bidang
Terdapat tiga kemungkinan kedudukan titik terhadap bidang, yaitu:
- Titik terletak pada bidang: Titik tersebut berada di permukaan bidang. Contohnya, titik A pada bidang ABCD.
- Titik terletak di luar bidang: Titik tersebut berada di luar permukaan bidang. Contohnya, titik E di luar bidang ABCD.
- Titik terletak di dalam bidang: Titik tersebut berada di dalam ruang yang dibatasi oleh bidang. Contohnya, titik F di dalam bidang ABCD.
Ilustrasi Kedudukan Titik terhadap Bidang
Berikut adalah ilustrasi untuk setiap kemungkinan kedudukan titik terhadap bidang:
- Titik terletak pada bidang: Bayangkan sebuah meja datar sebagai bidang. Titik yang berada tepat di atas permukaan meja, misalnya titik yang menandai pusat meja, terletak pada bidang meja.
- Titik terletak di luar bidang: Bayangkan sebuah bola di atas meja. Titik yang berada di permukaan bola, misalnya titik yang menandai puncak bola, terletak di luar bidang meja.
- Titik terletak di dalam bidang: Bayangkan sebuah kotak yang berada di dalam ruangan. Titik yang berada di dalam kotak, misalnya titik yang menandai pusat kotak, terletak di dalam bidang ruangan.
Tabel Kedudukan Titik terhadap Bidang
| Kedudukan Titik | Ilustrasi | Contoh |
|---|---|---|
| Titik terletak pada bidang | Titik yang berada tepat di atas permukaan meja. | Titik yang menandai pusat meja. |
| Titik terletak di luar bidang | Titik yang berada di permukaan bola di atas meja. | Titik yang menandai puncak bola. |
| Titik terletak di dalam bidang | Titik yang berada di dalam kotak yang berada di dalam ruangan. | Titik yang menandai pusat kotak. |
Kedudukan Garis terhadap Garis
Dalam geometri ruang, garis-garis dapat menempati berbagai posisi relatif satu sama lain. Memahami kedudukan ini penting untuk menyelesaikan berbagai masalah geometri dan visualisasi bentuk ruang.
Kedudukan Garis Terhadap Garis, Contoh soal kedudukan titik garis dan bidang dalam ruang
Ada tiga kemungkinan kedudukan garis terhadap garis dalam ruang, yaitu:
- Garis sejajar: Dua garis sejajar jika mereka berada pada bidang yang sama dan tidak pernah berpotongan. Garis sejajar memiliki arah yang sama.
- Garis berpotongan: Dua garis berpotongan jika mereka memiliki satu titik potong. Garis berpotongan tidak memiliki arah yang sama.
- Garis bersilangan: Dua garis bersilangan jika mereka tidak berada pada bidang yang sama dan tidak berpotongan. Garis bersilangan tidak memiliki arah yang sama dan tidak berpotongan.
Kedudukan Garis terhadap Bidang
Dalam geometri ruang, garis dan bidang dapat memiliki berbagai posisi relatif satu sama lain. Memahami hubungan antara garis dan bidang penting untuk menyelesaikan masalah geometri ruang, terutama dalam menentukan jarak, sudut, dan volume.
Kemungkinan Kedudukan Garis terhadap Bidang
Terdapat empat kemungkinan kedudukan garis terhadap bidang, yaitu:
- Garis terletak di dalam bidang: Garis ini sepenuhnya berada di dalam bidang, dengan semua titiknya berada di bidang tersebut.
- Garis memotong bidang: Garis ini menembus bidang pada satu titik. Titik potong ini merupakan satu-satunya titik yang dimiliki garis dan bidang.
- Garis sejajar dengan bidang: Garis ini tidak pernah berpotongan dengan bidang, meskipun dapat diproyeksikan ke bidang tersebut. Jarak antara garis dan bidang selalu sama.
- Garis tegak lurus dengan bidang: Garis ini membentuk sudut siku-siku dengan bidang. Sudut antara garis dan setiap garis yang terletak di bidang adalah 90 derajat.
Contoh Ilustrasi
Berikut adalah ilustrasi untuk setiap kemungkinan kedudukan garis terhadap bidang:
- Garis terletak di dalam bidang: Bayangkan sebuah meja datar (bidang). Garis yang menggambarkan tepi meja tersebut terletak di dalam bidang meja.
- Garis memotong bidang: Bayangkan sebuah pensil (garis) yang menembus selembar kertas (bidang). Titik tempat pensil menembus kertas merupakan titik potong antara garis dan bidang.
- Garis sejajar dengan bidang: Bayangkan sebuah jalan lurus (garis) yang membentang di sepanjang sebuah lapangan datar (bidang). Jalan tersebut tidak pernah berpotongan dengan lapangan, meskipun dapat diproyeksikan ke lapangan tersebut.
- Garis tegak lurus dengan bidang: Bayangkan sebuah tiang bendera (garis) yang berdiri tegak di atas tanah (bidang). Tiang bendera membentuk sudut siku-siku dengan tanah.
Tabel Kedudukan Garis terhadap Bidang
| Kedudukan | Ilustrasi | Contoh |
|---|---|---|
| Garis terletak di dalam bidang | Bayangkan sebuah meja datar (bidang). Garis yang menggambarkan tepi meja tersebut terletak di dalam bidang meja. | Garis yang menghubungkan dua titik pada permukaan sebuah meja. |
| Garis memotong bidang | Bayangkan sebuah pensil (garis) yang menembus selembar kertas (bidang). Titik tempat pensil menembus kertas merupakan titik potong antara garis dan bidang. | Garis yang menghubungkan dua titik pada permukaan sebuah bola, yang dipotong oleh sebuah bidang. |
| Garis sejajar dengan bidang | Bayangkan sebuah jalan lurus (garis) yang membentang di sepanjang sebuah lapangan datar (bidang). Jalan tersebut tidak pernah berpotongan dengan lapangan, meskipun dapat diproyeksikan ke lapangan tersebut. | Garis yang menghubungkan dua titik pada permukaan sebuah silinder, yang sejajar dengan bidang alas silinder. |
| Garis tegak lurus dengan bidang | Bayangkan sebuah tiang bendera (garis) yang berdiri tegak di atas tanah (bidang). Tiang bendera membentuk sudut siku-siku dengan tanah. | Garis yang menghubungkan pusat sebuah lingkaran dengan titik pada lingkaran tersebut, jika bidang lingkaran tersebut tegak lurus terhadap garis. |
Kedudukan Bidang terhadap Bidang
Dalam geometri ruang, kita dapat mengamati berbagai kemungkinan kedudukan antara dua bidang. Mempelajari hal ini membantu kita memahami hubungan dan interaksi antar bidang dalam ruang tiga dimensi. Berikut adalah beberapa kemungkinan kedudukan bidang terhadap bidang:
Kemungkinan Kedudukan Bidang terhadap Bidang
Ada beberapa kemungkinan kedudukan yang dapat terjadi antara dua bidang, yaitu:
- Berpotongan: Dua bidang dikatakan berpotongan jika keduanya memiliki garis persekutuan. Garis persekutuan ini merupakan garis yang terletak pada kedua bidang tersebut. Contoh: Dua buah dinding yang saling berpotongan membentuk sudut siku-siku, garis persekutuannya adalah garis yang membatasi kedua dinding tersebut.
- Sejajar: Dua bidang dikatakan sejajar jika keduanya tidak memiliki titik persekutuan. Artinya, kedua bidang tersebut tidak akan pernah bertemu, meskipun diperpanjang hingga tak terhingga. Contoh: Dua buah dinding yang saling berhadapan dan tidak berpotongan, keduanya sejajar.
- Berimpit: Dua bidang dikatakan berimpit jika keduanya memiliki semua titik yang sama. Artinya, kedua bidang tersebut sebenarnya adalah bidang yang sama. Contoh: Dua buah kaca yang saling bertumpuk, keduanya berimpit.
Ilustrasi Kedudukan Bidang terhadap Bidang
Berikut adalah ilustrasi untuk setiap kemungkinan kedudukan bidang terhadap bidang:
- Berpotongan: Bayangkan dua lembar kertas yang saling berpotongan, membentuk sudut tertentu. Garis persekutuannya adalah garis yang membatasi kedua lembar kertas tersebut.
- Sejajar: Bayangkan dua lembar kertas yang diletakkan sejajar satu sama lain, tanpa berpotongan. Kedua lembar kertas tersebut akan tetap sejajar meskipun diperpanjang hingga tak terhingga.
- Berimpit: Bayangkan dua lembar kertas yang saling bertumpuk, sehingga keduanya terlihat seperti satu lembar kertas. Kedua lembar kertas tersebut memiliki semua titik yang sama, sehingga dikatakan berimpit.
Tabel Kedudukan Bidang terhadap Bidang
| Kedudukan | Ilustrasi | Contoh |
|---|---|---|
| Berpotongan | Dua lembar kertas yang saling berpotongan, membentuk sudut tertentu. | Dua buah dinding yang saling berpotongan membentuk sudut siku-siku. |
| Sejajar | Dua lembar kertas yang diletakkan sejajar satu sama lain, tanpa berpotongan. | Dua buah dinding yang saling berhadapan dan tidak berpotongan. |
| Berimpit | Dua lembar kertas yang saling bertumpuk, sehingga keduanya terlihat seperti satu lembar kertas. | Dua buah kaca yang saling bertumpuk. |
Rumus Jarak Titik ke Garis
Dalam geometri ruang, menentukan jarak titik ke garis merupakan salah satu konsep penting. Pengetahuan ini dapat diterapkan dalam berbagai bidang, seperti menentukan jarak terdekat antara titik dan garis lurus pada objek tiga dimensi. Jarak titik ke garis didefinisikan sebagai panjang garis tegak lurus yang ditarik dari titik tersebut ke garis. Untuk menghitung jarak titik ke garis dalam ruang, kita dapat menggunakan rumus yang melibatkan vektor dan operasi perkalian silang.
Rumus Jarak Titik ke Garis
Rumus untuk menghitung jarak titik ke garis dalam ruang adalah:
Jarak = |(P – Q) x v| / |v|
Keterangan:
- P adalah titik yang ingin dihitung jaraknya ke garis.
- Q adalah titik yang terletak pada garis.
- v adalah vektor arah garis.
- |(P – Q) x v| adalah panjang vektor hasil perkalian silang antara vektor (P – Q) dan v.
- |v| adalah panjang vektor arah garis.
Contoh Soal dan Penyelesaian
Misalkan kita ingin menghitung jarak titik A(1, 2, 3) ke garis yang melalui titik B(2, 1, 0) dan memiliki vektor arah v = (1, -1, 2).
- Tentukan vektor (P – Q) = (A – B) = (1 – 2, 2 – 1, 3 – 0) = (-1, 1, 3).
- Hitung perkalian silang (P – Q) x v = (-1, 1, 3) x (1, -1, 2) = (5, 5, 0).
- Hitung panjang vektor hasil perkalian silang |(P – Q) x v| = √(5² + 5² + 0²) = 5√2.
- Hitung panjang vektor arah garis |v| = √(1² + (-1)² + 2²) = √6.
- Hitung jarak titik A ke garis: Jarak = |(P – Q) x v| / |v| = (5√2) / √6 = (5√3) / 3.
Jadi, jarak titik A(1, 2, 3) ke garis yang melalui titik B(2, 1, 0) dan memiliki vektor arah v = (1, -1, 2) adalah (5√3) / 3 satuan.
Langkah-langkah Menghitung Jarak Titik ke Garis dengan Ilustrasi Gambar
Untuk lebih memahami proses menghitung jarak titik ke garis, berikut langkah-langkah yang disertai ilustrasi gambar:
- Tentukan titik P yang ingin dihitung jaraknya ke garis dan titik Q yang terletak pada garis.
- Tentukan vektor arah garis v.
- Hitung vektor (P – Q).
- Hitung perkalian silang (P – Q) x v. Vektor hasil perkalian silang ini tegak lurus terhadap kedua vektor (P – Q) dan v.
- Hitung panjang vektor hasil perkalian silang |(P – Q) x v|. Panjang ini mewakili panjang proyeksi vektor (P – Q) pada bidang yang tegak lurus terhadap garis.
- Hitung panjang vektor arah garis |v|.
- Bagilah panjang vektor hasil perkalian silang dengan panjang vektor arah garis: Jarak = |(P – Q) x v| / |v|.
Ilustrasi gambar:
Bayangkan titik P berada di luar garis, titik Q berada pada garis, dan vektor v adalah vektor arah garis. Vektor (P – Q) adalah vektor yang menghubungkan titik P dan Q. Vektor hasil perkalian silang (P – Q) x v tegak lurus terhadap garis dan juga tegak lurus terhadap vektor (P – Q). Panjang vektor hasil perkalian silang ini mewakili jarak terpendek dari titik P ke garis, yaitu panjang garis tegak lurus yang ditarik dari titik P ke garis.
Rumus Jarak Titik ke Bidang
Menentukan jarak titik ke bidang dalam ruang adalah salah satu konsep penting dalam geometri ruang. Jarak ini didefinisikan sebagai jarak terpendek antara titik tersebut dengan bidang. Rumus yang digunakan untuk menghitung jarak titik ke bidang melibatkan proyeksi titik tersebut pada bidang dan vektor normal bidang.
Rumus Jarak Titik ke Bidang
Misalkan titik A(x1, y1, z1) dan bidang π dengan persamaan ax + by + cz + d = 0. Jarak titik A ke bidang π dapat dihitung dengan rumus:
Jarak(A, π) = |ax1 + by1 + cz1 + d| / √(a2 + b2 + c2)
Keterangan:
- Jarak(A, π) adalah jarak titik A ke bidang π.
- a, b, dan c adalah koefisien dari persamaan bidang π.
- d adalah konstanta dalam persamaan bidang π.
- x1, y1, dan z1 adalah koordinat titik A.
Contoh Soal dan Penyelesaian
Misalkan titik A(2, 1, -3) dan bidang π dengan persamaan 2x – y + 3z – 5 = 0. Hitunglah jarak titik A ke bidang π.
Penyelesaian:
- Tentukan nilai a, b, c, d, x1, y1, dan z1 dari soal.
- Substitusikan nilai-nilai tersebut ke dalam rumus jarak titik ke bidang.
- Hitung jarak(A, π) = |2(2) – 1(1) + 3(-3) – 5| / √(22 + (-1)2 + 32) = 10 / √14 = 5√14 / 7.
Jadi, jarak titik A(2, 1, -3) ke bidang π dengan persamaan 2x – y + 3z – 5 = 0 adalah 5√14 / 7.
Langkah-langkah Menghitung Jarak Titik ke Bidang
Berikut langkah-langkah menghitung jarak titik ke bidang:
- Tentukan persamaan bidang dan koordinat titik.
- Tentukan vektor normal bidang. Vektor normal bidang adalah vektor yang tegak lurus terhadap bidang. Koefisien dari persamaan bidang (a, b, c) merupakan vektor normal bidang.
- Tentukan titik pada bidang. Titik pada bidang dapat diperoleh dengan mensubstitusikan nilai x, y, atau z yang sebarang ke dalam persamaan bidang dan menyelesaikan persamaan tersebut.
- Tentukan vektor yang menghubungkan titik pada bidang dengan titik yang ingin dihitung jaraknya.
- Proyeksikan vektor tersebut pada vektor normal bidang. Proyeksi vektor pada vektor normal bidang adalah panjang vektor tersebut dikalikan dengan cosinus sudut antara vektor tersebut dengan vektor normal bidang.
- Jarak titik ke bidang adalah panjang proyeksi vektor tersebut pada vektor normal bidang.
Ilustrasi gambar:
Gambarlah titik A(x1, y1, z1) dan bidang π dengan persamaan ax + by + cz + d = 0. Gambarlah vektor normal bidang (a, b, c) dan vektor yang menghubungkan titik A dengan titik pada bidang. Proyeksikan vektor tersebut pada vektor normal bidang. Panjang proyeksi vektor tersebut adalah jarak titik A ke bidang π.
Rumus Jarak Garis ke Garis
Menghitung jarak antara dua garis dalam ruang merupakan konsep penting dalam geometri ruang. Jarak tersebut mewakili jarak terpendek antara dua garis yang tidak sejajar atau berpotongan. Rumus jarak garis ke garis digunakan untuk menentukan jarak minimum tersebut.
Rumus Jarak Garis ke Garis
Rumus untuk menghitung jarak antara dua garis dalam ruang adalah sebagai berikut:
Jarak = |(a x b) . c| / |a x b|
Dimana:
- a adalah vektor arah garis pertama.
- b adalah vektor arah garis kedua.
- c adalah vektor yang menghubungkan titik pada garis pertama ke titik pada garis kedua.
- a x b adalah perkalian silang antara vektor a dan b, yang menghasilkan vektor normal terhadap bidang yang dibentuk oleh kedua garis.
- (a x b) . c adalah hasil perkalian dot antara vektor normal dan vektor c, yang menghasilkan proyeksi vektor c pada vektor normal.
- |a x b| adalah panjang vektor normal.
Contoh Soal dan Penyelesaian
Misalkan terdapat dua garis dalam ruang:
- Garis pertama: x = 1 + 2t, y = 2 – t, z = 3 + t
- Garis kedua: x = 2 + s, y = 1 + 2s, z = 4 – s
Tentukan jarak antara kedua garis tersebut.
Penyelesaian:
1. Menentukan vektor arah garis pertama (a) dan garis kedua (b):
- a = (2, -1, 1)
- b = (1, 2, -1)
2. Menentukan vektor c yang menghubungkan titik pada garis pertama ke titik pada garis kedua:
- Ambil titik (1, 2, 3) pada garis pertama dan titik (2, 1, 4) pada garis kedua.
- c = (2, 1, 4) – (1, 2, 3) = (1, -1, 1)
3. Menghitung perkalian silang antara vektor a dan b (a x b):
- a x b = (-1, -3, -5)
4. Menghitung perkalian dot antara (a x b) dan c:
- (a x b) . c = (-1, -3, -5) . (1, -1, 1) = -1 + 3 – 5 = -3
5. Menghitung panjang vektor normal (a x b):
- |a x b| = √((-1)² + (-3)² + (-5)²) = √35
6. Menghitung jarak antara kedua garis:
- Jarak = |(a x b) . c| / |a x b| = |-3| / √35 = 3/√35
Jadi, jarak antara kedua garis tersebut adalah 3/√35 satuan.
Ilustrasi Gambar
Ilustrasi gambar menunjukkan dua garis yang tidak sejajar dan tidak berpotongan dalam ruang. Garis pertama berwarna merah dan garis kedua berwarna biru. Vektor arah garis pertama (a) dan garis kedua (b) ditunjukkan sebagai panah merah dan biru. Vektor c yang menghubungkan titik pada garis pertama ke titik pada garis kedua ditunjukkan sebagai panah hijau. Vektor normal (a x b) ditunjukkan sebagai panah ungu. Jarak antara kedua garis diwakili oleh garis tegak lurus berwarna hitam.
Rumus Jarak Garis ke Bidang
Menentukan jarak antara garis dan bidang dalam ruang merupakan salah satu konsep penting dalam geometri ruang. Pengetahuan ini berguna untuk memahami hubungan spasial antara garis dan bidang, serta dalam menyelesaikan berbagai permasalahan geometri ruang.
Rumus Jarak Garis ke Bidang
Rumus untuk menghitung jarak garis ke bidang adalah sebagai berikut:
Jarak garis ke bidang = |Proyeksi vektor arah garis ke vektor normal bidang| / |vektor normal bidang|
Rumus ini menunjukkan bahwa jarak garis ke bidang adalah panjang proyeksi vektor arah garis ke vektor normal bidang, dibagi dengan panjang vektor normal bidang.
Contoh Soal dan Penyelesaian
Misalkan kita memiliki garis l dengan persamaan vektor r = (1, 2, 3) + t(2, 1, -1) dan bidang π dengan persamaan 2x + y – z = 5. Untuk menentukan jarak antara garis l dan bidang π, kita dapat mengikuti langkah-langkah berikut:
Langkah-langkah Menghitung Jarak Garis ke Bidang
- Tentukan vektor arah garis v. Vektor arah garis l adalah (2, 1, -1).
- Tentukan vektor normal bidang n. Vektor normal bidang π adalah (2, 1, -1).
- Hitung proyeksi vektor arah garis ke vektor normal bidang. Proyeksi vektor v ke vektor n adalah (v · n) / |n|² * n = (2 * 2 + 1 * 1 – 1 * -1) / (2² + 1² + (-1)²) * (2, 1, -1) = (6/6) * (2, 1, -1) = (2, 1, -1).
- Hitung panjang proyeksi vektor arah garis ke vektor normal bidang. Panjang proyeksi vektor v ke vektor n adalah |(2, 1, -1)| = √(2² + 1² + (-1)²) = √6.
- Hitung panjang vektor normal bidang. Panjang vektor n adalah |(2, 1, -1)| = √(2² + 1² + (-1)²) = √6.
- Hitung jarak garis ke bidang. Jarak garis l ke bidang π adalah |(2, 1, -1)| / |(2, 1, -1)| = √6 / √6 = 1.
Ilustrasi Gambar
Untuk mempermudah pemahaman, perhatikan ilustrasi gambar berikut:
Gambar menunjukkan garis l dan bidang π dalam ruang. Vektor v adalah vektor arah garis l, sedangkan n adalah vektor normal bidang π. Proyeksi vektor v ke vektor n ditunjukkan dengan garis putus-putus. Panjang proyeksi vektor v ke vektor n merupakan jarak antara garis l dan bidang π.
Kesimpulan
Dengan menggunakan rumus dan langkah-langkah yang telah dijelaskan, kita dapat menghitung jarak antara garis dan bidang dalam ruang. Rumus ini membantu kita memahami hubungan spasial antara garis dan bidang, serta dalam menyelesaikan berbagai permasalahan geometri ruang.
Penerapan Konsep Kedudukan Titik, Garis, dan Bidang dalam Kehidupan Nyata: Contoh Soal Kedudukan Titik Garis Dan Bidang Dalam Ruang
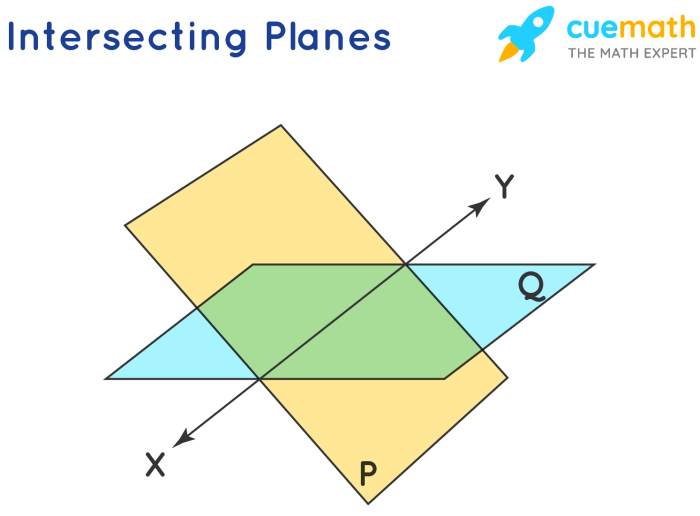
Konsep kedudukan titik, garis, dan bidang dalam ruang bukan hanya teori abstrak yang dipelajari di bangku sekolah. Konsep ini memiliki aplikasi yang luas dan nyata dalam berbagai bidang kehidupan, seperti arsitektur, teknik, dan seni. Penerapannya memungkinkan para ahli di bidangnya untuk memecahkan masalah dan membuat keputusan yang lebih tepat dan efektif.
Arsitektur
Konsep kedudukan titik, garis, dan bidang sangat penting dalam arsitektur. Arsitek menggunakan konsep ini untuk mendesain bangunan yang kokoh, fungsional, dan estetis. Contohnya, dalam mendesain sebuah gedung bertingkat, arsitek perlu mempertimbangkan kedudukan titik-titik penyangga, garis-garis struktur, dan bidang-bidang dinding dan atap. Kedudukan titik-titik penyangga menentukan kekuatan struktur bangunan, sedangkan garis-garis struktur menentukan arah aliran beban. Bidang-bidang dinding dan atap menentukan bentuk dan fungsi ruangan. Dengan memahami konsep ini, arsitek dapat memastikan bahwa bangunan yang mereka desain stabil, aman, dan memenuhi kebutuhan penghuninya.
Penutupan
Memahami konsep kedudukan titik, garis, dan bidang dalam ruang merupakan langkah awal untuk memahami geometri ruang. Dengan memahami konsep ini, kita dapat memecahkan masalah yang lebih kompleks dan membuat keputusan yang lebih tepat dalam berbagai bidang. Konsep ini tidak hanya bermanfaat dalam dunia akademis, tetapi juga dalam kehidupan sehari-hari, membantu kita memahami dan menavigasi dunia tiga dimensi yang kita tinggali.





