Pernahkah Anda mendengar istilah kuartil? Istilah ini mungkin terdengar asing bagi sebagian orang, tetapi sebenarnya kuartil merupakan konsep penting dalam statistik yang membantu kita memahami bagaimana data terbagi dan terdistribusi. Dalam artikel ini, kita akan menjelajahi contoh soal kuartil data tunggal genap, sebuah konsep yang memungkinkan kita untuk membagi data menjadi empat bagian yang sama besar. Dengan memahami kuartil, kita dapat memperoleh wawasan yang lebih dalam tentang karakteristik data dan menarik kesimpulan yang lebih akurat.
Kuartil data tunggal genap memiliki karakteristik unik karena jumlah datanya genap. Hal ini menyebabkan cara perhitungan kuartilnya berbeda dengan data tunggal ganjil. Artikel ini akan membahas rumus, langkah-langkah, dan contoh soal yang akan membantu Anda memahami cara menghitung kuartil data tunggal genap dengan mudah. Selain itu, kita akan melihat bagaimana kuartil dapat diterapkan dalam berbagai bidang kehidupan sehari-hari, mulai dari ekonomi hingga pendidikan.
Pengertian Kuartil Data Tunggal Genap
Kuartil merupakan salah satu ukuran pemusatan data yang membagi data menjadi empat bagian yang sama besar. Dalam data tunggal genap, kuartil dihitung dengan rumus khusus yang mempertimbangkan jumlah data yang genap.
Pengertian Kuartil Data Tunggal Genap
Kuartil data tunggal genap adalah nilai yang membagi data menjadi empat bagian yang sama besar, dengan jumlah data yang genap. Kuartil pada data tunggal genap dibagi menjadi tiga, yaitu kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3).
Perbedaan Kuartil Data Tunggal Genap dan Ganjil
Perbedaan utama antara kuartil data tunggal genap dan ganjil terletak pada rumus yang digunakan untuk menghitungnya. Pada data tunggal genap, rumus yang digunakan melibatkan pembagian data menjadi dua bagian yang sama, sedangkan pada data tunggal ganjil, rumus yang digunakan melibatkan pemilihan data tengah.
- Pada data tunggal genap, rumus yang digunakan untuk menentukan kuartil adalah:
Q1 = data ke- (n/4)
Q2 = (data ke- (n/2) + data ke- (n/2 + 1))/2
Q3 = data ke- (3n/4)
- Pada data tunggal ganjil, rumus yang digunakan untuk menentukan kuartil adalah:
Q1 = data ke- ((n+1)/4)
Q2 = data ke- ((n+1)/2)
Q3 = data ke- (3(n+1)/4)
Dimana n adalah jumlah data.
Contoh Data Tunggal Genap dan Cara Menentukan Kuartilnya
Misalkan kita memiliki data tunggal genap berikut: 2, 4, 6, 8, 10, 12. Untuk menentukan kuartilnya, kita dapat menggunakan rumus yang telah disebutkan sebelumnya.
- Q1 = data ke- (n/4) = data ke- (6/4) = data ke- 1.5. Karena data ke- 1.5 tidak ada, maka kita mengambil rata-rata dari data ke- 1 dan data ke- 2, yaitu (2 + 4)/2 = 3. Jadi, Q1 = 3.
- Q2 = (data ke- (n/2) + data ke- (n/2 + 1))/2 = (data ke- (6/2) + data ke- (6/2 + 1))/2 = (data ke- 3 + data ke- 4)/2 = (6 + 8)/2 = 7. Jadi, Q2 = 7.
- Q3 = data ke- (3n/4) = data ke- (3*6/4) = data ke- 4.5. Karena data ke- 4.5 tidak ada, maka kita mengambil rata-rata dari data ke- 4 dan data ke- 5, yaitu (8 + 10)/2 = 9. Jadi, Q3 = 9.
Dengan demikian, kuartil dari data tunggal genap 2, 4, 6, 8, 10, 12 adalah Q1 = 3, Q2 = 7, dan Q3 = 9.
Rumus Kuartil Data Tunggal Genap
Kuartil merupakan salah satu ukuran pemusatan data yang membagi data menjadi empat bagian yang sama. Kuartil data tunggal genap memiliki rumus khusus untuk menentukan kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3). Rumus ini membantu kita memahami distribusi data dan mengidentifikasi nilai-nilai yang membagi data menjadi empat bagian yang sama.
Rumus Kuartil Data Tunggal Genap
Rumus kuartil data tunggal genap adalah sebagai berikut:
Qi = (i/4) (n + 1)
di mana:
- Qi adalah kuartil ke-i (Q1, Q2, atau Q3)
- i adalah nomor kuartil (1, 2, atau 3)
- n adalah jumlah data
Contoh Penerapan Rumus Kuartil Data Tunggal Genap
Misalnya, kita memiliki data nilai ujian 10 siswa sebagai berikut: 70, 75, 80, 85, 90, 95, 100, 105, 110, 115.
Untuk menentukan kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3) dari data tersebut, kita dapat menggunakan rumus di atas:
- Q1 = (1/4) (10 + 1) = 2,75. Karena Q1 merupakan nilai tengah antara data ke-2 dan ke-3, maka Q1 = (75 + 80)/2 = 77,5.
- Q2 = (2/4) (10 + 1) = 5,5. Karena Q2 merupakan nilai tengah antara data ke-5 dan ke-6, maka Q2 = (90 + 95)/2 = 92,5.
- Q3 = (3/4) (10 + 1) = 8,25. Karena Q3 merupakan nilai tengah antara data ke-8 dan ke-9, maka Q3 = (105 + 110)/2 = 107,5.
Dari hasil perhitungan di atas, kita dapat melihat bahwa:
- 25% dari nilai ujian berada di bawah 77,5.
- 50% dari nilai ujian berada di bawah 92,5.
- 75% dari nilai ujian berada di bawah 107,5.
Langkah-Langkah Menghitung Kuartil Data Tunggal Genap
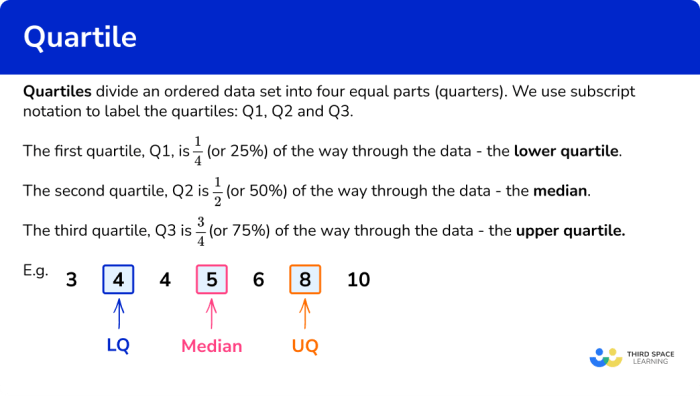
Kuartil merupakan ukuran statistik yang membagi data menjadi empat bagian yang sama. Kuartil pertama (Q1) membagi 25% data terkecil, kuartil kedua (Q2) merupakan median yang membagi 50% data terkecil, dan kuartil ketiga (Q3) membagi 75% data terkecil. Pada data tunggal genap, langkah-langkah menghitung kuartil sedikit berbeda dengan data tunggal ganjil. Berikut ini adalah langkah-langkah yang sistematis untuk menghitung kuartil data tunggal genap:
Langkah-Langkah Menghitung Kuartil Data Tunggal Genap
Untuk menghitung kuartil data tunggal genap, kita perlu memperhatikan posisi kuartil yang ingin dicari. Posisi kuartil ditentukan dengan rumus:
Posisi Qi = (i/4) * (n + 1)
Contoh soal kuartil data tunggal genap bisa dibilang gampang, kan? Tinggal urutkan datanya, terus cari nilai tengahnya. Nah, kalau udah dapet nilai tengah, kamu bisa cari kuartil pertama dan ketiga. Tapi, kalo kamu lagi pengen tantangan, coba deh cek contoh soal pertidaksamaan rasional dan irasional di sini.
Soal-soal ini bakal menguji kemampuanmu dalam menyelesaikan pertidaksamaan dengan variabel di penyebut atau di dalam akar. Setelah berjibaku dengan pertidaksamaan, kamu bisa kembali ke soal kuartil data tunggal genap, dan berasa lebih mudah, kan?
di mana:
- Qi adalah kuartil ke-i (i = 1, 2, 3)
- n adalah jumlah data
Setelah mendapatkan posisi kuartil, langkah-langkah selanjutnya adalah:
- Urutkan data dari yang terkecil hingga yang terbesar.
- Hitung posisi kuartil menggunakan rumus di atas.
- Jika posisi kuartil adalah bilangan bulat, maka kuartil adalah data yang berada pada posisi tersebut.
- Jika posisi kuartil adalah bilangan pecahan, maka kuartil adalah rata-rata dari data yang berada pada posisi sebelum dan sesudah posisi kuartil.
Contoh Perhitungan Kuartil Data Tunggal Genap
Misalkan kita memiliki data tinggi badan 8 siswa (dalam cm) sebagai berikut:
| No. | Tinggi Badan (cm) |
|---|---|
| 1 | 160 |
| 2 | 165 |
| 3 | 168 |
| 4 | 170 |
| 5 | 172 |
| 6 | 175 |
| 7 | 178 |
| 8 | 180 |
Langkah-langkah menghitung kuartil data tunggal genap adalah sebagai berikut:
- Urutkan data dari yang terkecil hingga yang terbesar: 160, 165, 168, 170, 172, 175, 178, 180.
- Hitung posisi kuartil:
- Posisi Q1 = (1/4) * (8 + 1) = 2,25
- Posisi Q2 = (2/4) * (8 + 1) = 4,5
- Posisi Q3 = (3/4) * (8 + 1) = 6,75
- Karena posisi Q1 dan Q3 adalah bilangan pecahan, maka kita perlu menghitung rata-rata dari data yang berada pada posisi sebelum dan sesudah posisi kuartil:
- Q1 = (data pada posisi 2 + data pada posisi 3) / 2 = (165 + 168) / 2 = 166,5 cm
- Q3 = (data pada posisi 6 + data pada posisi 7) / 2 = (175 + 178) / 2 = 176,5 cm
- Karena posisi Q2 adalah bilangan bulat, maka Q2 adalah data yang berada pada posisi tersebut, yaitu Q2 = 170 cm.
Perbedaan Menghitung Kuartil Data Tunggal Genap dan Ganjil
Perbedaan utama dalam menghitung kuartil data tunggal genap dan ganjil terletak pada rumus posisi kuartil. Pada data tunggal genap, rumus posisi kuartil adalah (i/4) * (n + 1), sedangkan pada data tunggal ganjil, rumus posisi kuartil adalah (i/4) * (n + 0,5). Hal ini disebabkan karena pada data tunggal ganjil, median berada di tengah data, sedangkan pada data tunggal genap, median adalah rata-rata dari dua data di tengah.
Sebagai contoh, pada data tunggal ganjil dengan jumlah data 7, posisi Q2 adalah (2/4) * (7 + 0,5) = 3,625. Karena posisi Q2 adalah bilangan pecahan, maka Q2 adalah rata-rata dari data yang berada pada posisi 3 dan 4.
Contoh Soal Kuartil Data Tunggal Genap
Kuartil merupakan salah satu ukuran pemusatan data yang membagi data menjadi empat bagian yang sama besar. Dalam data tunggal genap, kita perlu memperhatikan cara menghitung kuartil karena jumlah data yang genap.
Contoh Soal Kuartil Data Tunggal Genap
Berikut ini tiga contoh soal tentang menghitung kuartil data tunggal genap dengan tingkat kesulitan yang berbeda.
- Contoh Soal 1 (Tingkat Kesulitan Rendah)
Data nilai ujian matematika dari 10 siswa adalah sebagai berikut: 70, 75, 80, 85, 90, 95, 100, 105, 110, 115. Hitunglah kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3) dari data tersebut.
Kuartil Rumus Hasil Q1 (n/4) = (10/4) = 2,5; data ke-3 = 80 Q1 = 80 Q2 (n/2) = (10/2) = 5; data ke-5 dan ke-6 dijumlahkan lalu dibagi 2 = (90+95)/2 Q2 = 92,5 Q3 (3n/4) = (30/4) = 7,5; data ke-8 = 105 Q3 = 105 - Contoh Soal 2 (Tingkat Kesulitan Sedang)
Data tinggi badan 12 siswa dalam cm adalah sebagai berikut: 150, 155, 160, 165, 170, 175, 180, 185, 190, 195, 200, 205. Hitunglah kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3) dari data tersebut.
Kuartil Rumus Hasil Q1 (n/4) = (12/4) = 3; data ke-3 = 160 Q1 = 160 Q2 (n/2) = (12/2) = 6; data ke-6 dan ke-7 dijumlahkan lalu dibagi 2 = (175+180)/2 Q2 = 177,5 Q3 (3n/4) = (36/4) = 9; data ke-9 = 190 Q3 = 190 - Contoh Soal 3 (Tingkat Kesulitan Tinggi)
Data usia 14 orang karyawan di sebuah perusahaan adalah sebagai berikut: 25, 28, 30, 32, 35, 38, 40, 42, 45, 48, 50, 52, 55, 58. Hitunglah kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3) dari data tersebut.
Kuartil Rumus Hasil Q1 (n/4) = (14/4) = 3,5; data ke-4 = 32 Q1 = 32 Q2 (n/2) = (14/2) = 7; data ke-7 dan ke-8 dijumlahkan lalu dibagi 2 = (40+42)/2 Q2 = 41 Q3 (3n/4) = (42/4) = 10,5; data ke-11 = 50 Q3 = 50
Penerapan Kuartil Data Tunggal Genap dalam Kehidupan Sehari-hari
Konsep kuartil data tunggal genap, meskipun terdengar rumit, memiliki aplikasi yang luas dalam berbagai bidang kehidupan. Pemahaman tentang kuartil dapat membantu kita menganalisis data dan mengambil keputusan yang lebih tepat, baik dalam konteks ekonomi, sosial, maupun pendidikan.
Penerapan Kuartil dalam Ekonomi
Kuartil data tunggal genap dapat digunakan untuk menganalisis data ekonomi seperti pendapatan, harga barang, dan tingkat inflasi. Misalnya, dalam menganalisis distribusi pendapatan, kita dapat menggunakan kuartil untuk mengetahui persentase penduduk yang memiliki pendapatan di bawah, di atas, atau di sekitar median.
- Contoh: Data pendapatan penduduk di suatu daerah menunjukkan bahwa kuartil pertama (Q1) adalah Rp2.000.000, kuartil kedua (Q2) atau median adalah Rp3.500.000, dan kuartil ketiga (Q3) adalah Rp5.000.000. Dari data ini, kita dapat menyimpulkan bahwa 25% penduduk memiliki pendapatan di bawah Rp2.000.000, 50% memiliki pendapatan di bawah Rp3.500.000, dan 75% memiliki pendapatan di bawah Rp5.000.000.
Informasi ini sangat bermanfaat bagi pemerintah dalam merancang kebijakan ekonomi yang lebih adil dan merata.
Penerapan Kuartil dalam Sosial
Kuartil juga dapat digunakan untuk menganalisis data sosial seperti tingkat pendidikan, tingkat pengangguran, dan tingkat kriminalitas. Misalnya, dengan menganalisis kuartil tingkat pendidikan, kita dapat mengetahui persentase penduduk yang memiliki tingkat pendidikan di bawah, di atas, atau di sekitar median.
- Contoh: Data tingkat pendidikan di suatu daerah menunjukkan bahwa kuartil pertama (Q1) adalah 12 tahun, kuartil kedua (Q2) atau median adalah 15 tahun, dan kuartil ketiga (Q3) adalah 18 tahun. Dari data ini, kita dapat menyimpulkan bahwa 25% penduduk memiliki tingkat pendidikan di bawah 12 tahun, 50% memiliki tingkat pendidikan di bawah 15 tahun, dan 75% memiliki tingkat pendidikan di bawah 18 tahun.
Informasi ini sangat bermanfaat bagi lembaga sosial dalam merancang program-program sosial yang lebih efektif dan terarah.
Penerapan Kuartil dalam Pendidikan
Kuartil data tunggal genap dapat digunakan untuk menganalisis data pendidikan seperti nilai ujian, tingkat kelulusan, dan tingkat partisipasi siswa.
- Contoh: Data nilai ujian matematika di suatu kelas menunjukkan bahwa kuartil pertama (Q1) adalah 60, kuartil kedua (Q2) atau median adalah 75, dan kuartil ketiga (Q3) adalah 85. Dari data ini, kita dapat menyimpulkan bahwa 25% siswa memiliki nilai ujian di bawah 60, 50% memiliki nilai ujian di bawah 75, dan 75% memiliki nilai ujian di bawah 85.
Informasi ini sangat bermanfaat bagi guru dalam mengevaluasi kinerja siswa dan merancang strategi pembelajaran yang lebih efektif.
Perbedaan Kuartil Data Tunggal Genap dan Ganjil: Contoh Soal Kuartil Data Tunggal Genap
Kuartil adalah nilai yang membagi data menjadi empat bagian yang sama. Dalam menghitung kuartil, kita perlu membedakan antara data tunggal genap dan ganjil. Perbedaan ini terletak pada rumus dan langkah-langkah perhitungannya.
Perbedaan Cara Menghitung Kuartil Data Tunggal Genap dan Ganjil
Berikut tabel perbandingan yang menunjukkan perbedaan cara menghitung kuartil data tunggal genap dan ganjil:
| Kuartil | Data Tunggal Genap | Data Tunggal Ganjil |
|---|---|---|
| Q1 | (n/4) + 1 | (n + 1)/4 |
| Q2 | (n/2) + 1 | (n + 1)/2 |
| Q3 | (3n/4) + 1 | (3n + 1)/4 |
Perbedaan Rumus dan Langkah-langkah Perhitungan
Rumus dan langkah-langkah perhitungan kuartil untuk data tunggal genap dan ganjil berbeda karena jumlah data yang dibagi menjadi empat bagian sama tidak selalu bulat. Berikut penjelasannya:
-
Data Tunggal Genap:
Rumus yang digunakan untuk menghitung kuartil pada data tunggal genap adalah (n/k) + 1, di mana n adalah jumlah data dan k adalah urutan kuartil (1 untuk Q1, 2 untuk Q2, dan 3 untuk Q3). Langkah-langkahnya adalah:
- Urutkan data dari yang terkecil hingga terbesar.
- Hitung jumlah data (n).
- Hitung nilai (n/k) + 1 untuk masing-masing kuartil.
- Jika hasil perhitungan adalah bilangan bulat, maka kuartilnya adalah data pada urutan tersebut.
- Jika hasil perhitungan bukan bilangan bulat, maka kuartilnya adalah rata-rata dari data pada urutan sebelum dan sesudah hasil perhitungan.
-
Data Tunggal Ganjil:
Rumus yang digunakan untuk menghitung kuartil pada data tunggal ganjil adalah (n + 1)/k, di mana n adalah jumlah data dan k adalah urutan kuartil (1 untuk Q1, 2 untuk Q2, dan 3 untuk Q3). Langkah-langkahnya adalah:
- Urutkan data dari yang terkecil hingga terbesar.
- Hitung jumlah data (n).
- Hitung nilai (n + 1)/k untuk masing-masing kuartil.
- Jika hasil perhitungan adalah bilangan bulat, maka kuartilnya adalah data pada urutan tersebut.
- Jika hasil perhitungan bukan bilangan bulat, maka kuartilnya adalah rata-rata dari data pada urutan sebelum dan sesudah hasil perhitungan.
Contoh Perhitungan Kuartil Data Tunggal Genap dan Ganjil
Berikut contoh data tunggal genap dan ganjil dan perbedaan hasil perhitungan kuartilnya:
Data Tunggal Genap
Misalnya, kita memiliki data tunggal genap: 2, 4, 5, 6, 8, 10. Jumlah data (n) adalah 6.
-
Q1: (n/4) + 1 = (6/4) + 1 = 2.5. Karena hasilnya bukan bilangan bulat, maka Q1 adalah rata-rata dari data pada urutan ke-2 dan ke-3, yaitu (4 + 5)/2 = 4.5.
-
Q2: (n/2) + 1 = (6/2) + 1 = 4. Karena hasilnya adalah bilangan bulat, maka Q2 adalah data pada urutan ke-4, yaitu 6.
-
Q3: (3n/4) + 1 = (3*6/4) + 1 = 5.5. Karena hasilnya bukan bilangan bulat, maka Q3 adalah rata-rata dari data pada urutan ke-5 dan ke-6, yaitu (8 + 10)/2 = 9.
Data Tunggal Ganjil
Misalnya, kita memiliki data tunggal ganjil: 3, 5, 7, 9, 11. Jumlah data (n) adalah 5.
-
Q1: (n + 1)/4 = (5 + 1)/4 = 1.5. Karena hasilnya bukan bilangan bulat, maka Q1 adalah rata-rata dari data pada urutan ke-1 dan ke-2, yaitu (3 + 5)/2 = 4.
-
Q2: (n + 1)/2 = (5 + 1)/2 = 3. Karena hasilnya adalah bilangan bulat, maka Q2 adalah data pada urutan ke-3, yaitu 7.
-
Q3: (3n + 1)/4 = (3*5 + 1)/4 = 4. Karena hasilnya adalah bilangan bulat, maka Q3 adalah data pada urutan ke-4, yaitu 9.
Hubungan Kuartil dengan Ukuran Pemusatan Data
Kuartil adalah ukuran statistik yang membagi data menjadi empat bagian yang sama. Kuartil memberikan informasi tentang penyebaran data dan letak relatif nilai-nilai dalam distribusi data. Hubungan antara kuartil dengan ukuran pemusatan data seperti mean, median, dan modus, dapat memberikan gambaran yang lebih lengkap tentang karakteristik data.
Kuartil dan Mean
Mean (rata-rata) adalah ukuran pemusatan data yang dipengaruhi oleh semua nilai data. Kuartil, khususnya kuartil pertama (Q1) dan kuartil ketiga (Q3), dapat memberikan informasi tentang simetri data dan kemungkinan adanya outlier. Jika mean lebih besar dari median (Q2), data cenderung miring ke kanan (positif). Sebaliknya, jika mean lebih kecil dari median, data cenderung miring ke kiri (negatif).
Kuartil dan Median
Median (Q2) adalah nilai tengah dari data yang terurut. Median tidak dipengaruhi oleh outlier, sehingga memberikan gambaran yang lebih akurat tentang pusat data dibandingkan dengan mean jika data mengandung outlier. Kuartil pertama (Q1) dan kuartil ketiga (Q3) memberikan informasi tentang penyebaran data di sekitar median. Selisih antara Q3 dan Q1 (disebut rentang interkuartil) menunjukkan seberapa tersebar data di sekitar median.
Kuartil dan Modus
Modus adalah nilai yang paling sering muncul dalam data. Kuartil tidak secara langsung terkait dengan modus. Namun, kuartil dapat memberikan informasi tentang bentuk distribusi data, yang dapat membantu dalam menentukan apakah data unimodal (memiliki satu modus) atau multimodal (memiliki lebih dari satu modus).
Contoh Penggunaan Kuartil
Misalnya, kita memiliki data tentang tinggi badan siswa di sebuah kelas. Mean tinggi badan adalah 165 cm, mediannya 163 cm, dan modus 160 cm. Kuartil pertama (Q1) adalah 158 cm, dan kuartil ketiga (Q3) adalah 172 cm. Dari data ini, kita dapat melihat bahwa mean lebih besar dari median, yang menunjukkan bahwa data cenderung miring ke kanan. Rentang interkuartil (Q3 – Q1) adalah 14 cm, yang menunjukkan bahwa data tersebar cukup merata di sekitar median. Modus 160 cm menunjukkan bahwa ada lebih banyak siswa dengan tinggi badan 160 cm dibandingkan dengan tinggi badan lainnya.
Informasi Tambahan dari Kuartil
Kuartil memberikan informasi tambahan tentang distribusi data selain ukuran pemusatan. Misalnya, rentang interkuartil (IQR) dapat digunakan untuk mengidentifikasi outlier. Outlier adalah nilai yang jauh berbeda dari nilai-nilai lainnya dalam data. Nilai yang lebih kecil dari Q1 – 1,5*IQR atau lebih besar dari Q3 + 1,5*IQR dianggap sebagai outlier.
Kuartil dalam Analisis Data Statistik
Kuartil adalah ukuran statistik yang membagi data menjadi empat bagian yang sama. Kuartil digunakan untuk mengidentifikasi dan menganalisis distribusi data, memberikan gambaran tentang penyebaran data dan lokasi data pada skala pengukuran.
Pengertian dan Jenis Kuartil, Contoh soal kuartil data tunggal genap
Kuartil adalah nilai-nilai yang membagi data menjadi empat bagian yang sama. Ada tiga jenis kuartil, yaitu:
- Kuartil pertama (Q1): Memisahkan 25% data terendah dari 75% data tertinggi.
- Kuartil kedua (Q2): Memisahkan 50% data terendah dari 50% data tertinggi. Q2 sama dengan median data.
- Kuartil ketiga (Q3): Memisahkan 75% data terendah dari 25% data tertinggi.
Peran Kuartil dalam Analisis Data Statistik
Kuartil memainkan peran penting dalam analisis data statistik karena memberikan informasi tentang penyebaran data dan lokasi data pada skala pengukuran. Kuartil membantu dalam:
- Menganalisis penyebaran data: Jarak antara kuartil menunjukkan seberapa tersebar data. Jangkauan antar kuartil (IQR), yaitu selisih antara Q3 dan Q1, memberikan gambaran tentang penyebaran 50% data tengah.
- Mengidentifikasi outlier: Data yang berada di luar jangkauan IQR dianggap sebagai outlier. Outlier adalah data yang jauh dari data lainnya dan dapat memengaruhi hasil analisis statistik.
- Membandingkan distribusi data: Kuartil dapat digunakan untuk membandingkan distribusi data dari dua kelompok berbeda. Misalnya, dengan membandingkan IQR dari dua kelompok data, kita dapat mengetahui kelompok mana yang memiliki penyebaran data yang lebih besar.
Cara Menghitung Kuartil
Untuk menghitung kuartil, data harus terlebih dahulu diurutkan dari yang terkecil hingga yang terbesar. Rumus untuk menghitung kuartil adalah:
Qi = (i/4) * (n + 1)
Dimana:
- Qi adalah kuartil ke-i (i = 1, 2, 3)
- n adalah jumlah data
Jika hasil perhitungan Qi adalah bilangan bulat, maka kuartil adalah nilai data ke-Qi. Jika hasil perhitungan Qi adalah bilangan desimal, maka kuartil adalah rata-rata dari nilai data ke-Qi dan nilai data ke-Qi + 1.
Contoh Perhitungan Kuartil
Misalkan kita memiliki data berikut:
- 2, 4, 5, 6, 7, 8, 9, 10, 11, 12
Untuk menghitung kuartil pertama (Q1):
Q1 = (1/4) * (10 + 1) = 2.75
Karena hasil perhitungan Q1 adalah bilangan desimal, maka Q1 adalah rata-rata dari nilai data ke-2 dan ke-3, yaitu:
Q1 = (4 + 5) / 2 = 4.5
Dengan cara yang sama, kita dapat menghitung Q2 dan Q3:
Q2 = (2/4) * (10 + 1) = 5.5
Q3 = (3/4) * (10 + 1) = 8.25
Karena hasil perhitungan Q2 adalah bilangan desimal, maka Q2 adalah rata-rata dari nilai data ke-5 dan ke-6, yaitu:
Q2 = (7 + 8) / 2 = 7.5
Karena hasil perhitungan Q3 adalah bilangan desimal, maka Q3 adalah rata-rata dari nilai data ke-8 dan ke-9, yaitu:
Q3 = (9 + 10) / 2 = 9.5
Jadi, kuartil untuk data tersebut adalah:
- Q1 = 4.5
- Q2 = 7.5
- Q3 = 9.5
Contoh Penggunaan Kuartil dalam Analisis Data
Misalkan kita ingin membandingkan distribusi nilai ujian matematika dari dua kelas, kelas A dan kelas B. Data nilai ujian matematika dari kedua kelas tersebut adalah:
| Kelas | Nilai Ujian |
|---|---|
| A | 60, 65, 70, 75, 80, 85, 90, 95, 100 |
| B | 50, 55, 60, 65, 70, 75, 80, 85, 90 |
Dengan menghitung kuartil untuk kedua kelas, kita dapat membandingkan penyebaran data nilai ujian matematika dari kedua kelas tersebut. Kuartil untuk kelas A adalah:
- Q1 = 70
- Q2 = 80
- Q3 = 90
Kuartil untuk kelas B adalah:
- Q1 = 55
- Q2 = 65
- Q3 = 80
Dari hasil perhitungan kuartil, kita dapat melihat bahwa:
- IQR kelas A adalah 20 (90 – 70), sedangkan IQR kelas B adalah 25 (80 – 55). Ini menunjukkan bahwa penyebaran data nilai ujian matematika di kelas B lebih besar daripada di kelas A.
- Median nilai ujian matematika di kelas A adalah 80, sedangkan median nilai ujian matematika di kelas B adalah 65. Ini menunjukkan bahwa nilai ujian matematika di kelas A cenderung lebih tinggi daripada di kelas B.
Kesimpulannya, dengan menggunakan kuartil, kita dapat membandingkan distribusi data nilai ujian matematika dari kedua kelas dan melihat bahwa kelas B memiliki penyebaran data yang lebih besar dan nilai ujian matematika yang cenderung lebih rendah daripada kelas A.
Kuartil dalam Konteks Data Berkelompok
Kuartil merupakan salah satu ukuran pemusatan data yang membagi data menjadi empat bagian yang sama. Dalam konteks data tunggal, kita telah mempelajari cara menghitung kuartil dengan mudah. Namun, bagaimana dengan data berkelompok? Data berkelompok merupakan data yang disusun dalam tabel frekuensi, dimana data dikelompokkan ke dalam kelas-kelas tertentu.
Menghitung Kuartil pada Data Berkelompok
Menghitung kuartil pada data berkelompok sedikit berbeda dengan data tunggal. Hal ini karena kita tidak lagi memiliki data individu, melainkan data yang sudah dikelompokkan. Berikut adalah langkah-langkah menghitung kuartil pada data berkelompok:
- Menentukan letak kuartil:
- Kuartil pertama (Q1) terletak pada data ke-¼n, dimana n adalah jumlah data.
- Kuartil kedua (Q2) terletak pada data ke-½n, yang merupakan median.
- Kuartil ketiga (Q3) terletak pada data ke-¾n.
- Menentukan kelas kuartil:
- Setelah menentukan letak kuartil, kita perlu menentukan kelas mana yang memuat letak kuartil tersebut. Misalnya, jika letak Q1 berada pada data ke-25, dan kelas pertama memiliki frekuensi kumulatif 20, maka kelas kedua merupakan kelas yang memuat Q1.
- Menghitung nilai kuartil:
- Setelah menentukan kelas kuartil, kita dapat menghitung nilai kuartil dengan menggunakan rumus:
- Keterangan:
- Qi adalah nilai kuartil ke-i (i = 1, 2, 3)
- Lb adalah batas bawah kelas kuartil
- n adalah jumlah data
- Fk-1 adalah frekuensi kumulatif kelas sebelum kelas kuartil
- fk adalah frekuensi kelas kuartil
- c adalah panjang kelas
Qi = Lb + ( ( (n/4)i – Fk-1) / fk ) * c
Contoh Perhitungan Kuartil pada Data Berkelompok
Misalnya, kita memiliki data berkelompok tentang tinggi badan siswa kelas 10 seperti tabel berikut:
| Kelas Tinggi Badan (cm) | Frekuensi | Frekuensi Kumulatif |
|---|---|---|
| 150 – 155 | 5 | 5 |
| 155 – 160 | 10 | 15 |
| 160 – 165 | 15 | 30 |
| 165 – 170 | 12 | 42 |
| 170 – 175 | 8 | 50 |
Kita ingin menghitung Q1, Q2, dan Q3 dari data tersebut. Berikut langkah-langkahnya:
- Menentukan letak kuartil:
- Q1 terletak pada data ke-¼n = ¼ * 50 = 12.5
- Q2 terletak pada data ke-½n = ½ * 50 = 25
- Q3 terletak pada data ke-¾n = ¾ * 50 = 37.5
- Menentukan kelas kuartil:
- Q1 terletak pada kelas 155 – 160 karena frekuensi kumulatif kelas sebelumnya (150 – 155) adalah 5, sedangkan letak Q1 (12.5) berada di antara 5 dan 15.
- Q2 terletak pada kelas 160 – 165 karena frekuensi kumulatif kelas sebelumnya (155 – 160) adalah 15, sedangkan letak Q2 (25) berada di antara 15 dan 30.
- Q3 terletak pada kelas 165 – 170 karena frekuensi kumulatif kelas sebelumnya (160 – 165) adalah 30, sedangkan letak Q3 (37.5) berada di antara 30 dan 42.
- Menghitung nilai kuartil:
- Q1 = Lb + ( ( (n/4)1 – Fk-1) / fk ) * c = 155 + ( ( (50/4)1 – 5) / 10) * 5 = 157.5
- Q2 = Lb + ( ( (n/4)2 – Fk-1) / fk ) * c = 160 + ( ( (50/4)2 – 15) / 15) * 5 = 161.67
- Q3 = Lb + ( ( (n/4)3 – Fk-1) / fk ) * c = 165 + ( ( (50/4)3 – 30) / 12) * 5 = 167.08
Jadi, Q1 = 157.5 cm, Q2 = 161.67 cm, dan Q3 = 167.08 cm.
Penerapan Kuartil dalam Penelitian
Kuartil merupakan salah satu alat statistik yang berguna dalam menganalisis data dan menarik kesimpulan yang lebih akurat. Kuartil membagi data menjadi empat bagian yang sama, dengan masing-masing bagian mewakili 25% dari total data. Dalam penelitian ilmiah, kuartil dapat digunakan untuk memahami distribusi data, mengidentifikasi outlier, dan membandingkan kelompok data.
Penggunaan Kuartil dalam Analisis Data
Kuartil dapat digunakan untuk menganalisis data dalam berbagai cara. Berikut adalah beberapa contoh:
- Menentukan Rentang Interkuartil (IQR): IQR merupakan ukuran penyebaran data yang menunjukkan perbedaan antara kuartil ketiga (Q3) dan kuartil pertama (Q1). IQR membantu dalam mengidentifikasi outlier dan memahami variasi data.
- Membandingkan Distribusi Data: Kuartil dapat digunakan untuk membandingkan distribusi data dari dua atau lebih kelompok. Misalnya, dalam penelitian tentang pengaruh jenis pupuk terhadap hasil panen, peneliti dapat membandingkan IQR hasil panen dari kelompok yang menggunakan pupuk A dengan kelompok yang menggunakan pupuk B.
- Menganalisis Tren Data: Kuartil dapat membantu dalam mengidentifikasi tren data seiring waktu. Misalnya, dalam penelitian tentang perubahan suhu rata-rata tahunan, peneliti dapat menganalisis tren data dengan melihat perubahan kuartil pertama, kedua, dan ketiga selama beberapa tahun.
Contoh Penelitian yang Menggunakan Kuartil
Misalnya, dalam penelitian tentang pengaruh program pelatihan terhadap kinerja karyawan, peneliti dapat menggunakan kuartil untuk menganalisis distribusi skor kinerja karyawan sebelum dan sesudah mengikuti program pelatihan.
Peneliti dapat membandingkan IQR skor kinerja kedua kelompok untuk melihat apakah program pelatihan memberikan dampak signifikan terhadap kinerja karyawan. Selain itu, peneliti juga dapat menganalisis perubahan kuartil pertama, kedua, dan ketiga untuk melihat bagaimana program pelatihan mempengaruhi distribusi skor kinerja secara keseluruhan.
Manfaat Kuartil dalam Memahami Distribusi Data
Kuartil memberikan informasi yang lebih lengkap tentang distribusi data dibandingkan dengan hanya menggunakan mean atau median.
Kuartil membantu peneliti dalam:
- Menentukan outlier: Data yang berada di luar rentang IQR dapat dianggap sebagai outlier. Outlier dapat memengaruhi analisis data, sehingga perlu diidentifikasi dan ditangani dengan tepat.
- Memahami bentuk distribusi data: Kuartil membantu peneliti dalam memahami apakah data terdistribusi secara simetris atau tidak. Jika kuartil pertama dan ketiga memiliki jarak yang sama dengan median, maka data terdistribusi secara simetris.
- Membuat kesimpulan yang lebih akurat: Dengan memahami distribusi data melalui kuartil, peneliti dapat membuat kesimpulan yang lebih akurat tentang populasi berdasarkan sampel data.
Penutup
Memahami konsep kuartil data tunggal genap merupakan langkah penting dalam memahami statistik. Dengan memahami bagaimana data terbagi menjadi empat bagian yang sama besar, kita dapat memperoleh pemahaman yang lebih mendalam tentang karakteristik data dan menarik kesimpulan yang lebih akurat. Dengan demikian, kuartil menjadi alat yang berharga dalam analisis data dan pengambilan keputusan yang lebih tepat.




