Contoh soal limit x mendekati 0 – Pernahkah kamu membayangkan bagaimana sebuah fungsi berperilaku saat nilai inputnya semakin mendekati suatu titik tertentu? Konsep limit dalam kalkulus membantu kita memahami perilaku fungsi di sekitar titik tersebut, meskipun fungsi mungkin tidak terdefinisi di titik itu sendiri. Salah satu contoh yang menarik adalah limit fungsi x mendekati 0. Bayangkan sebuah kereta api yang melaju menuju stasiun. Saat kereta mendekati stasiun, kecepatannya berkurang secara bertahap hingga akhirnya berhenti tepat di titik tujuan. Limit fungsi x mendekati 0 mirip dengan perilaku kereta api ini, di mana kita mengamati bagaimana nilai fungsi berubah saat x mendekati 0.

Dalam artikel ini, kita akan menjelajahi konsep limit fungsi x mendekati 0, membahas contoh soal, dan mempelajari berbagai metode untuk menentukan nilai limit. Kita juga akan membahas aplikasi limit fungsi dalam berbagai bidang, seperti kalkulus, fisika, dan ekonomi.

Table of Contents:

Pengertian Limit Fungsi

Limit fungsi merupakan konsep dasar dalam kalkulus yang menjelaskan perilaku suatu fungsi ketika variabel input mendekati suatu nilai tertentu. Konsep ini sangat penting karena memungkinkan kita untuk menganalisis fungsi dan memprediksi nilainya di sekitar titik tertentu, bahkan jika fungsi tersebut tidak terdefinisi di titik tersebut.

Contoh Ilustrasi Limit Fungsi

Bayangkan sebuah mobil yang melaju di jalan raya. Kita ingin mengetahui kecepatan mobil tersebut pada saat mobil melewati titik tertentu di jalan. Meskipun kita tidak dapat secara langsung mengukur kecepatan mobil tepat pada saat melewati titik tersebut, kita dapat memperkirakan kecepatannya dengan melihat kecepatan mobil pada saat mendekati titik tersebut. Semakin dekat mobil ke titik tersebut, semakin akurat estimasi kecepatan kita.

Dalam contoh ini, titik di jalan raya merupakan titik yang ingin kita cari limitnya. Kecepatan mobil pada saat mendekati titik tersebut merupakan nilai limit fungsi. Semakin dekat mobil ke titik tersebut, semakin dekat nilai fungsi (kecepatan) ke nilai limitnya.

Perbedaan Limit Fungsi dan Nilai Fungsi

Limit fungsi dan nilai fungsi adalah konsep yang berbeda meskipun keduanya terkait erat. Limit fungsi menunjukkan perilaku fungsi ketika variabel input mendekati suatu nilai tertentu, sedangkan nilai fungsi adalah nilai yang dihasilkan fungsi pada input tertentu.

Limit fungsi menunjukkan kecenderungan fungsi ketika variabel input mendekati suatu nilai, tidak peduli apakah fungsi terdefinisi di titik tersebut atau tidak.
Nilai fungsi adalah nilai yang dihasilkan fungsi ketika variabel input dimasukkan ke dalam fungsi tersebut. Nilai fungsi hanya terdefinisi jika fungsi terdefinisi di titik tersebut.

Sebagai contoh, perhatikan fungsi f(x) = x^2. Limit fungsi f(x) ketika x mendekati 2 adalah 4. Artinya, ketika x mendekati 2, nilai fungsi f(x) mendekati 4. Nilai fungsi f(2) adalah 4, yang sama dengan nilai limitnya.

Namun, perhatikan fungsi g(x) = 1/x. Limit fungsi g(x) ketika x mendekati 0 adalah tak hingga. Artinya, ketika x mendekati 0, nilai fungsi g(x) menjadi sangat besar. Namun, nilai fungsi g(0) tidak terdefinisi, karena pembagian dengan 0 tidak didefinisikan.

Limit Fungsi x Mendekati 0

Limit fungsi x mendekati 0 merupakan konsep penting dalam kalkulus. Konsep ini membantu kita memahami bagaimana nilai suatu fungsi berubah ketika nilai x mendekati 0, baik dari sisi kiri maupun kanan.

Contoh Soal Limit Fungsi x Mendekati 0

Berikut contoh soal limit fungsi x mendekati 0:

Tentukan nilai limit dari fungsi f(x) = (x^2 + 2x) / x ketika x mendekati 0.

Cara Menentukan Nilai Limit Fungsi x Mendekati 0

Untuk menentukan nilai limit fungsi x mendekati 0, kita dapat menggunakan beberapa cara:

Substitusi langsung: Jika fungsi kontinu di x = 0, kita dapat langsung substitusikan nilai x = 0 ke dalam fungsi.
Penyederhanaan aljabar: Jika fungsi tidak kontinu di x = 0, kita dapat mencoba menyederhanakan fungsi tersebut terlebih dahulu sebelum melakukan substitusi.
Metode grafik: Kita dapat membuat grafik fungsi dan mengamati nilai fungsi ketika x mendekati 0 dari kiri dan kanan.

Tabel Nilai Fungsi untuk x Mendekati 0

Berikut tabel yang menunjukkan nilai fungsi f(x) = (x^2 + 2x) / x untuk x mendekati 0 dari kiri dan kanan:

x	f(x)
-0.1	-1.9
-0.01	-1.99
-0.001	-1.999
0	Tidak terdefinisi
0.001	2.001
0.01	2.01
0.1	2.1

Metode Penghitungan Limit

Limit fungsi merupakan konsep penting dalam kalkulus yang menjelaskan perilaku fungsi saat variabel mendekati suatu nilai tertentu. Ada beberapa metode yang dapat digunakan untuk menghitung limit fungsi, dan dua di antaranya adalah metode substitusi langsung dan metode faktorisasi.

Metode Substitusi Langsung

Metode substitusi langsung merupakan metode yang paling sederhana untuk menghitung limit fungsi. Metode ini melibatkan penggantian nilai yang didekati oleh variabel ke dalam fungsi. Jika hasil dari substitusi tersebut adalah nilai yang terdefinisi, maka nilai tersebut merupakan nilai limit fungsi.

Contoh Soal: Hitung limit fungsi f(x) = x² + 2x + 1 saat x mendekati 2.
Penyelesaian:

Dengan substitusi langsung, kita dapatkan:

lim_x→2 f(x) = lim_x→2 (x² + 2x + 1) = (2)² + 2(2) + 1 = 9.

Jadi, limit fungsi f(x) = x² + 2x + 1 saat x mendekati 2 adalah 9.

Metode Faktorisasi

Metode faktorisasi digunakan untuk menghitung limit fungsi yang menghasilkan bentuk tak tentu (0/0) setelah substitusi langsung. Metode ini melibatkan pemfaktoran ekspresi fungsi dan kemudian menyederhanakannya sebelum melakukan substitusi.

Contoh Soal: Hitung limit fungsi f(x) = (x² – 4) / (x – 2) saat x mendekati 2.
Penyelesaian:

Dengan substitusi langsung, kita dapatkan:

lim_x→2 f(x) = lim_x→2 (x² – 4) / (x – 2) = (2² – 4) / (2 – 2) = 0/0 (bentuk tak tentu).

Untuk menyelesaikan bentuk tak tentu ini, kita dapat memfaktorkan ekspresi fungsi:

lim_x→2 f(x) = lim_x→2 (x² – 4) / (x – 2) = lim_x→2 (x + 2)(x – 2) / (x – 2) = lim_x→2 (x + 2) = 2 + 2 = 4.

Jadi, limit fungsi f(x) = (x² – 4) / (x – 2) saat x mendekati 2 adalah 4.

Limit Fungsi Tak Hingga: Contoh Soal Limit X Mendekati 0

Limit fungsi tak hingga merupakan konsep penting dalam kalkulus yang membahas perilaku fungsi saat variabel independen mendekati tak hingga. Konsep ini membantu kita memahami bagaimana fungsi berperilaku pada nilai-nilai yang sangat besar.

Pengertian Limit Fungsi Tak Hingga

Limit fungsi tak hingga merupakan nilai yang didekati oleh fungsi saat variabel independen mendekati tak hingga. Dengan kata lain, kita ingin mengetahui nilai fungsi saat variabel independen menjadi sangat besar.

Contoh Soal Limit Fungsi Tak Hingga

Sebagai contoh, perhatikan fungsi f(x) = 1/x. Ketika nilai x semakin besar, nilai f(x) semakin kecil dan mendekati nol. Kita dapat menuliskan ini sebagai limit:

lim_x→∞ 1/x = 0

Ini menunjukkan bahwa saat x mendekati tak hingga, nilai fungsi f(x) mendekati nol.

Cara Menentukan Nilai Limit Fungsi Tak Hingga

Ada beberapa cara untuk menentukan nilai limit fungsi tak hingga, tergantung pada jenis fungsi yang dihadapi. Berikut beberapa metode yang umum digunakan:

Metode Substitusi: Untuk fungsi rasional, kita dapat mencoba mensubstitusikan nilai tak hingga ke dalam fungsi. Jika hasilnya berupa bentuk tak tentu, seperti ∞/∞ atau 0/0, kita perlu menggunakan metode lain.
Metode Faktorisasi: Jika fungsi dapat difaktorkan, kita dapat menyederhanakan fungsi dan kemudian mensubstitusikan nilai tak hingga.
Metode Pembagian dengan Suku Berderajat Tertinggi: Untuk fungsi rasional, kita dapat membagi pembilang dan penyebut dengan suku berderajat tertinggi. Ini akan menghasilkan bentuk yang lebih sederhana yang memudahkan kita untuk menentukan nilai limit.
Metode Grafik: Kita dapat menggambar grafik fungsi dan melihat perilaku fungsi saat x mendekati tak hingga.

Aplikasi Limit Fungsi

Limit fungsi merupakan konsep dasar dalam kalkulus yang berperan penting dalam memahami perilaku fungsi di sekitar titik tertentu. Limit fungsi membantu kita menganalisis bagaimana nilai fungsi mendekati nilai tertentu saat variabel independen mendekati nilai tertentu.

Aplikasi Limit Fungsi dalam Kalkulus

Limit fungsi merupakan konsep dasar dalam kalkulus yang memiliki banyak aplikasi. Limit digunakan untuk mendefinisikan konsep turunan dan integral, yang merupakan alat utama dalam kalkulus untuk mempelajari perubahan dan akumulasi.

Turunan: Turunan fungsi di titik tertentu didefinisikan sebagai limit dari rasio perubahan fungsi terhadap perubahan variabel independen saat variabel independen mendekati titik tersebut. Dengan kata lain, turunan merupakan ukuran laju perubahan fungsi. Limit digunakan untuk mendefinisikan konsep turunan, yang kemudian digunakan untuk menentukan titik kritis, titik belok, dan sifat lain dari fungsi.
Integral: Integral fungsi didefinisikan sebagai limit dari jumlah luas persegi panjang yang mendekati daerah di bawah kurva fungsi. Limit digunakan untuk mendefinisikan konsep integral, yang kemudian digunakan untuk menghitung luas, volume, dan panjang lengkung.

Contoh Aplikasi Limit Fungsi dalam Kehidupan Sehari-hari

Limit fungsi dapat digunakan untuk menganalisis berbagai fenomena dalam kehidupan sehari-hari. Berikut beberapa contohnya:

Kecepatan: Kecepatan merupakan ukuran laju perubahan posisi terhadap waktu. Dalam kalkulus, kecepatan didefinisikan sebagai turunan dari fungsi posisi terhadap waktu. Turunan merupakan limit dari rasio perubahan posisi terhadap perubahan waktu saat perubahan waktu mendekati nol. Dengan kata lain, kecepatan merupakan limit dari perubahan posisi per satuan waktu.
Pertumbuhan: Pertumbuhan populasi, misalnya, dapat dimodelkan dengan menggunakan fungsi eksponensial. Limit fungsi dapat digunakan untuk menentukan laju pertumbuhan populasi pada waktu tertentu. Misalnya, limit fungsi pertumbuhan populasi saat waktu mendekati tak terhingga dapat digunakan untuk memprediksi populasi pada masa depan.

Aplikasi Limit Fungsi dalam Fisika

Limit fungsi memiliki banyak aplikasi dalam fisika, terutama dalam mempelajari gerakan, gaya, dan energi. Berikut beberapa contohnya:

Kecepatan dan Percepatan: Dalam fisika, kecepatan didefinisikan sebagai turunan dari fungsi posisi terhadap waktu, dan percepatan didefinisikan sebagai turunan dari fungsi kecepatan terhadap waktu. Limit digunakan untuk mendefinisikan konsep turunan, yang kemudian digunakan untuk mempelajari gerakan benda.
Gaya dan Energi: Gaya merupakan ukuran interaksi antara benda-benda. Dalam fisika, gaya didefinisikan sebagai turunan dari fungsi energi potensial terhadap posisi. Limit digunakan untuk mendefinisikan konsep turunan, yang kemudian digunakan untuk mempelajari gaya yang bekerja pada benda.

Aplikasi Limit Fungsi dalam Ekonomi

Limit fungsi juga memiliki aplikasi penting dalam ekonomi, terutama dalam mempelajari perilaku pasar, pertumbuhan ekonomi, dan analisis keuangan. Berikut beberapa contohnya:

Permintaan dan Penawaran: Dalam ekonomi, permintaan dan penawaran merupakan faktor utama yang menentukan harga suatu barang. Limit fungsi dapat digunakan untuk mempelajari bagaimana permintaan dan penawaran berubah saat harga berubah. Misalnya, limit fungsi permintaan saat harga mendekati nol dapat digunakan untuk memprediksi permintaan pada harga yang sangat rendah.
Pertumbuhan Ekonomi: Pertumbuhan ekonomi dapat dimodelkan dengan menggunakan fungsi eksponensial. Limit fungsi dapat digunakan untuk menentukan laju pertumbuhan ekonomi pada waktu tertentu. Misalnya, limit fungsi pertumbuhan ekonomi saat waktu mendekati tak terhingga dapat digunakan untuk memprediksi pertumbuhan ekonomi pada masa depan.

Soal Latihan Limit Fungsi

Setelah memahami konsep dasar limit fungsi, mari kita berlatih dengan beberapa contoh soal. Soal-soal ini akan membantu kamu untuk memahami cara menghitung limit fungsi dan mengaplikasikannya dalam berbagai situasi. Soal-soal ini disusun dengan tingkat kesulitan yang beragam, mulai dari yang mudah hingga yang lebih menantang.

Soal Latihan Tingkat Mudah

Berikut beberapa contoh soal latihan limit fungsi x mendekati 0 dengan tingkat kesulitan mudah:

Tentukan nilai limit dari fungsi f(x) = 2x + 1 ketika x mendekati 0.
Tentukan nilai limit dari fungsi f(x) = x² + 3x ketika x mendekati 0.
Tentukan nilai limit dari fungsi f(x) = 3x² – 2x + 5 ketika x mendekati 0.

Soal Latihan Tingkat Sedang

Contoh soal latihan limit fungsi x mendekati 0 dengan tingkat kesulitan sedang:

Tentukan nilai limit dari fungsi f(x) = (x² – 4) / (x – 2) ketika x mendekati 0.
Tentukan nilai limit dari fungsi f(x) = (sin x) / x ketika x mendekati 0.
Tentukan nilai limit dari fungsi f(x) = (1 – cos x) / x² ketika x mendekati 0.

Soal Latihan Tingkat Sulit

Contoh soal latihan limit fungsi x mendekati 0 dengan tingkat kesulitan sulit:

Tentukan nilai limit dari fungsi f(x) = (x³ + 2x² – 3x) / (x² – 1) ketika x mendekati 0.
Tentukan nilai limit dari fungsi f(x) = (e^x – 1) / x ketika x mendekati 0.
Tentukan nilai limit dari fungsi f(x) = (tan x) / x ketika x mendekati 0.

Langkah-langkah Penyelesaian Soal Latihan

Berikut langkah-langkah umum untuk menyelesaikan soal limit fungsi:

Substitusikan nilai x yang mendekati 0 ke dalam fungsi.
Jika hasilnya adalah bentuk tak tentu (misalnya 0/0, ∞/∞, atau 0 * ∞), maka gunakan metode lain untuk menyelesaikan limit, seperti:
- Faktorisasi: Sederhanakan fungsi dengan memfaktorkan ekspresi aljabar.
- Rasionalisasi: Kalikan pembilang dan penyebut dengan bentuk konjugat.
  
  Contoh soal limit x mendekati 0 seringkali muncul dalam kalkulus, misalnya “Tentukan nilai limit dari (sin x)/x saat x mendekati 0”. Nah, untuk memahami soal-soal seperti ini, kamu bisa menggunakan teknik analisis yang mirip dengan contoh soal 5w 1h, seperti yang bisa kamu temukan di contoh soal 5w 1h.
  
  Dengan menanyakan “siapa”, “apa”, “kapan”, “di mana”, “mengapa”, dan “bagaimana” pada soal limit x mendekati 0, kamu akan lebih mudah memahami konsep dan menyelesaikannya.
- Identitas Trigonometri: Gunakan identitas trigonometri untuk menyederhanakan fungsi.
- Teorema L’Hopital: Gunakan teorema L’Hopital untuk menyelesaikan limit yang berbentuk tak tentu.
Hitung nilai limit setelah menyederhanakan fungsi.

Tabel Solusi Soal Latihan

Soal	Solusi
f(x) = 2x + 1, x mendekati 0	lim_x→0 (2x + 1) = 2(0) + 1 = 1
f(x) = x² + 3x, x mendekati 0	lim_x→0 (x² + 3x) = (0)² + 3(0) = 0
f(x) = 3x² – 2x + 5, x mendekati 0	lim_x→0 (3x² – 2x + 5) = 3(0)² – 2(0) + 5 = 5
f(x) = (x² – 4) / (x – 2), x mendekati 0	lim_x→0 ((x² – 4) / (x – 2)) = ((0)² – 4) / (0 – 2) = 2
f(x) = (sin x) / x, x mendekati 0	lim_x→0 ((sin x) / x) = 1 (menggunakan identitas trigonometri)
f(x) = (1 – cos x) / x², x mendekati 0	lim_x→0 ((1 – cos x) / x²) = 1/2 (menggunakan identitas trigonometri)
f(x) = (x³ + 2x² – 3x) / (x² – 1), x mendekati 0	lim_x→0 ((x³ + 2x² – 3x) / (x² – 1)) = 0 (menggunakan faktorisasi)
f(x) = (e^x – 1) / x, x mendekati 0	lim_x→0 ((e^x – 1) / x) = 1 (menggunakan teorema L’Hopital)
f(x) = (tan x) / x, x mendekati 0	lim_x→0 ((tan x) / x) = 1 (menggunakan identitas trigonometri)

Kesalahan Umum dalam Menentukan Limit

Menentukan limit fungsi merupakan konsep dasar dalam kalkulus. Meskipun terlihat sederhana, beberapa kesalahan umum sering terjadi saat menghitung limit. Kesalahan-kesalahan ini bisa berakibat fatal dalam menyelesaikan soal dan dapat menyebabkan hasil yang tidak akurat. Berikut adalah beberapa kesalahan umum dan bagaimana cara menghindarinya.

Substitusi Langsung Tanpa Memeriksa Kondisi

Salah satu kesalahan paling umum adalah langsung mensubstitusikan nilai yang didekati ke fungsi tanpa memperhatikan kondisi limit. Jika nilai yang didekati membuat fungsi menjadi tak terdefinisi (misalnya, pembagian dengan nol), maka hasil substitusi langsung tidak valid.

Kesalahan: Menentukan limit dari fungsi f(x) = 1/x saat x mendekati 0 dengan langsung mensubstitusikan x = 0. Hasilnya akan menjadi 1/0, yang tak terdefinisi.
Cara Menghindari: Periksa terlebih dahulu apakah nilai yang didekati membuat fungsi menjadi tak terdefinisi. Jika ya, cari cara lain untuk menentukan limit, seperti dengan faktorisasi, pemfaktoran, atau menggunakan teorema L’Hopital.

Memasukkan Nilai yang Tidak Benar

Kesalahan lain yang sering terjadi adalah memasukkan nilai yang tidak benar saat menghitung limit. Hal ini bisa terjadi karena kesalahan dalam membaca soal atau ketidaktelitian dalam menghitung.

Kesalahan: Menentukan limit dari fungsi f(x) = x^2 + 2x saat x mendekati 2, tetapi memasukkan nilai x = 1. Hasilnya akan menjadi 3, bukan nilai limit yang sebenarnya.
Cara Menghindari: Baca soal dengan cermat dan perhatikan nilai yang didekati. Hitung dengan teliti dan pastikan nilai yang dimasukkan ke fungsi adalah nilai yang benar.

Mengabaikan Limit Sisi

Dalam beberapa kasus, limit kanan dan limit kiri suatu fungsi tidak sama. Jika hanya dihitung limit kanan atau kiri saja, maka hasil yang diperoleh tidak akurat.

Kesalahan: Menentukan limit dari fungsi f(x) = |x|/x saat x mendekati 0 dengan hanya menghitung limit kanan. Hasilnya akan menjadi 1, sedangkan limit kiri adalah -1. Jadi, limit fungsi ini tidak ada.
Cara Menghindari: Selalu periksa limit kanan dan limit kiri untuk memastikan bahwa keduanya sama. Jika tidak, maka limit fungsi tersebut tidak ada.

Mencampur Konsep Limit dengan Kontinuitas

Limit dan kontinuitas merupakan konsep yang berbeda. Meskipun suatu fungsi memiliki limit di suatu titik, belum tentu fungsi tersebut kontinu di titik tersebut.

Kesalahan: Memasukkan nilai yang didekati ke fungsi tanpa memperhatikan kondisi limit, sehingga menghasilkan nilai yang tidak terdefinisi.
Cara Menghindari: Pahami definisi limit dan kontinuitas dengan baik. Limit adalah nilai yang didekati oleh fungsi, sedangkan kontinuitas adalah sifat fungsi yang tidak terputus di suatu titik.

Kesimpulan

Kesalahan-kesalahan umum dalam menentukan limit bisa dihindari dengan memahami konsep limit dengan baik dan memperhatikan beberapa hal penting seperti kondisi limit, nilai yang didekati, limit sisi, dan kontinuitas. Dengan berlatih dan memahami konsep dengan benar, Anda dapat menghindari kesalahan-kesalahan ini dan mendapatkan hasil yang akurat.

Limit Fungsi Berbentuk Pecahan

Limit fungsi berbentuk pecahan adalah salah satu jenis limit yang sering dijumpai dalam kalkulus. Limit ini mengkaji perilaku fungsi ketika variabel independen mendekati nilai tertentu, khususnya ketika fungsi tersebut dinyatakan dalam bentuk pecahan.

Cara Menentukan Limit Fungsi Berbentuk Pecahan

Untuk menentukan limit fungsi berbentuk pecahan, kita dapat menggunakan beberapa metode, salah satunya adalah metode substitusi langsung. Jika kita mendapatkan hasil yang terdefinisi setelah melakukan substitusi, maka hasil tersebut adalah nilai limitnya. Namun, jika kita mendapatkan hasil tak terdefinisi seperti 0/0 atau ∞/∞, maka kita perlu menggunakan metode lain seperti pemfaktoran, perkalian dengan konjugat, atau teorema L’Hospital.

Contoh Soal Limit Fungsi Berbentuk Pecahan

Misalnya, kita ingin menentukan limit fungsi f(x) = (x^2 – 4)/(x – 2) ketika x mendekati 2. Jika kita langsung mensubstitusikan x = 2 ke dalam fungsi, kita akan mendapatkan hasil 0/0 yang tak terdefinisi. Oleh karena itu, kita perlu menggunakan metode lain.

Metode Pemfaktoran

Metode pemfaktoran dapat digunakan untuk menentukan limit fungsi berbentuk pecahan jika kita mendapatkan hasil tak terdefinisi setelah melakukan substitusi langsung. Dalam contoh sebelumnya, kita dapat memfaktorkan fungsi f(x) sebagai berikut:

f(x) = (x^2 – 4)/(x – 2) = (x + 2)(x – 2)/(x – 2)

Kemudian, kita dapat menyederhanakan fungsi tersebut dengan membagi kedua ruas dengan (x – 2), sehingga:

f(x) = x + 2

Sekarang, kita dapat langsung mensubstitusikan x = 2 ke dalam fungsi yang telah disederhanakan, sehingga:

lim (x->2) f(x) = lim (x->2) (x + 2) = 2 + 2 = 4

Jadi, limit fungsi f(x) = (x^2 – 4)/(x – 2) ketika x mendekati 2 adalah 4.

Limit Fungsi Trigonometri

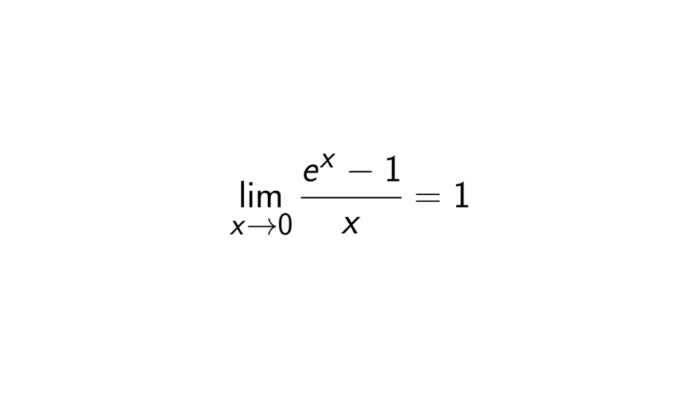
Limit fungsi trigonometri adalah konsep yang penting dalam kalkulus, yang melibatkan penentuan nilai fungsi trigonometri saat variabel bebas mendekati suatu nilai tertentu.

Cara Menentukan Limit Fungsi Trigonometri

Untuk menentukan limit fungsi trigonometri, kita dapat menggunakan berbagai teknik, termasuk:

Substitusi langsung: Jika fungsi kontinu di titik yang didekati, kita dapat langsung substitusikan nilai tersebut ke dalam fungsi untuk mendapatkan limitnya.
Identitas trigonometri: Kita dapat menggunakan identitas trigonometri untuk menyederhanakan fungsi dan memudahkan proses penentuan limit.
Teorema limit: Kita dapat menggunakan teorema limit untuk menghitung limit fungsi trigonometri yang lebih kompleks.

Limit Fungsi Eksponensial

Limit fungsi eksponensial adalah nilai yang didekati oleh fungsi eksponensial ketika variabel bebas mendekati nilai tertentu. Konsep ini penting dalam kalkulus karena memungkinkan kita untuk memahami perilaku fungsi di sekitar titik-titik tertentu, khususnya saat variabel bebas mendekati nilai yang tidak terdefinisi.

Cara Menentukan Limit Fungsi Eksponensial, Contoh soal limit x mendekati 0

Untuk menentukan limit fungsi eksponensial, kita dapat menggunakan beberapa cara, antara lain:

Substitusi langsung: Jika fungsi eksponensial terdefinisi untuk nilai yang didekati, kita dapat langsung mensubstitusikan nilai tersebut ke dalam fungsi untuk mendapatkan limitnya.
Sifat eksponensial: Kita dapat menggunakan sifat eksponensial untuk menyederhanakan fungsi eksponensial dan memudahkan penentuan limitnya.
Aturan L’Hopital: Jika fungsi eksponensial berbentuk tak tentu (seperti 0/0 atau ∞/∞), kita dapat menggunakan aturan L’Hopital untuk menentukan limitnya.

Contoh Soal Limit Fungsi Eksponensial

Berikut adalah contoh soal limit fungsi eksponensial:

Tentukan limit dari fungsi f(x) = e^x ketika x mendekati 0.

Untuk menyelesaikan soal ini, kita dapat menggunakan substitusi langsung:

lim (x→0) e^x = e^0 = 1

Jadi, limit dari fungsi f(x) = e^x ketika x mendekati 0 adalah 1.

Penggunaan Sifat Eksponensial

Sifat eksponensial dapat digunakan untuk menyederhanakan fungsi eksponensial dan memudahkan penentuan limitnya. Berikut adalah beberapa sifat eksponensial yang berguna:

e^0 = 1
e^∞ = ∞
e^-∞ = 0
e^(x+y) = e^x * e^y
e^(x-y) = e^x / e^y

Sebagai contoh, untuk menentukan limit dari fungsi f(x) = e^(x+2) ketika x mendekati -2, kita dapat menggunakan sifat e^(x+y) = e^x * e^y:

lim (x→-2) e^(x+2) = lim (x→-2) e^x * e^2 = e^-2 * e^2 = 1

Jadi, limit dari fungsi f(x) = e^(x+2) ketika x mendekati -2 adalah 1.

Contoh Soal Limit Fungsi Eksponensial Lainnya

Berikut adalah contoh soal limit fungsi eksponensial lainnya:

Tentukan limit dari fungsi f(x) = (e^x – 1) / x ketika x mendekati 0.

Fungsi ini berbentuk tak tentu (0/0) ketika x mendekati 0. Oleh karena itu, kita dapat menggunakan aturan L’Hopital untuk menentukan limitnya:

lim (x→0) (e^x – 1) / x = lim (x→0) e^x / 1 = e^0 = 1

Jadi, limit dari fungsi f(x) = (e^x – 1) / x ketika x mendekati 0 adalah 1.

Simpulan Akhir

Memahami konsep limit fungsi x mendekati 0 merupakan langkah penting dalam mempelajari kalkulus. Dengan memahami bagaimana fungsi berperilaku di sekitar titik tertentu, kita dapat menyelesaikan berbagai masalah matematika dan memahami berbagai fenomena di dunia nyata. Melalui contoh soal dan metode penghitungan yang telah dibahas, diharapkan kamu dapat menguasai konsep limit fungsi x mendekati 0 dan mengaplikasikannya dalam berbagai situasi.

Contoh Soal Limit Fungsi x Mendekati 0: Memahami Konsep Batas dalam Kalkulus