Contoh soal linear programming – Pernahkah Anda membayangkan bagaimana perusahaan besar menentukan strategi produksi yang paling menguntungkan? Atau bagaimana pemerintah mengalokasikan dana bantuan untuk program sosial yang paling efektif? Linear programming adalah alat matematika yang ampuh untuk menjawab pertanyaan-pertanyaan tersebut. Dengan menggunakan konsep linear programming, kita dapat memodelkan masalah kompleks dengan batasan tertentu, lalu mencari solusi optimal yang memaksimalkan keuntungan atau meminimalkan biaya.
Contoh soal linear programming membantu kita memahami penerapan konsep ini dalam kehidupan nyata. Melalui soal-soal, kita dapat belajar bagaimana membangun model matematika, menentukan fungsi objektif dan kendala, serta menemukan solusi optimal dengan menggunakan berbagai metode penyelesaian.
Pengertian Linear Programming
Linear programming adalah sebuah teknik optimasi matematika yang digunakan untuk menemukan solusi terbaik untuk masalah yang melibatkan kendala dan tujuan yang dinyatakan dalam bentuk linear. Sederhananya, linear programming membantu kita menemukan cara terbaik untuk menggunakan sumber daya yang terbatas untuk mencapai tujuan yang diinginkan.
Contoh Penerapan Linear Programming dalam Kehidupan Sehari-hari
Linear programming memiliki aplikasi yang luas dalam berbagai bidang, mulai dari bisnis, manufaktur, hingga kesehatan. Berikut beberapa contoh penerapannya dalam kehidupan sehari-hari:
- Perencanaan Produksi: Seorang produsen makanan ingin menentukan jumlah produk yang harus diproduksi untuk memaksimalkan keuntungan dengan mempertimbangkan keterbatasan bahan baku dan kapasitas produksi.
- Alokasi Sumber Daya: Sebuah perusahaan transportasi ingin mengalokasikan truk dan pengemudi untuk melayani rute pengiriman dengan biaya minimal dan memaksimalkan efisiensi.
- Perencanaan Diet: Seorang ahli gizi ingin merancang menu diet yang memenuhi kebutuhan nutrisi dengan biaya yang minimal.
Komponen Utama dalam Model Linear Programming
Model linear programming terdiri dari beberapa komponen utama yang saling berhubungan:
- Variabel Keputusan: Variabel yang mewakili kuantitas yang ingin diputuskan, seperti jumlah produk yang diproduksi, jumlah truk yang dialokasikan, atau jumlah kalori yang dikonsumsi.
- Fungsi Tujuan: Fungsi matematis yang mewakili tujuan yang ingin dicapai, seperti memaksimalkan keuntungan, meminimalkan biaya, atau memenuhi kebutuhan nutrisi.
- Kendala: Batasan atau persyaratan yang harus dipenuhi, seperti keterbatasan bahan baku, kapasitas produksi, atau anggaran.
Model Matematika Linear Programming
Linear programming adalah metode matematika yang digunakan untuk menyelesaikan masalah optimasi dengan batasan linier. Model matematika linear programming terdiri dari fungsi objektif dan kendala. Fungsi objektif adalah fungsi matematika yang ingin dioptimalkan, sedangkan kendala adalah batasan yang harus dipenuhi oleh solusi.
Perbedaan Model Matematika Linear Programming dan Non-Linear Programming
Perbedaan utama antara model matematika linear programming dan non-linear programming terletak pada fungsi objektif dan kendala. Dalam model linear programming, fungsi objektif dan kendala adalah fungsi linier, yaitu fungsi yang hanya memiliki variabel dengan pangkat satu. Sebaliknya, dalam model non-linear programming, fungsi objektif dan kendala dapat berupa fungsi non-linier, yaitu fungsi yang memiliki variabel dengan pangkat lebih besar dari satu atau fungsi trigonometri, logaritma, atau eksponensial.
| Karakteristik | Linear Programming | Non-Linear Programming |
|---|---|---|
| Fungsi Objektif | Linier | Non-linier |
| Kendala | Linier | Non-linier |
| Metode Penyelesaian | Metode Simplex | Metode Numerik (misalnya, metode Newton-Raphson) |
| Contoh Masalah | Perencanaan Produksi, Masalah Transportasi | Perencanaan Investasi, Masalah Optimasi Portofolio |
Persamaan Umum Model Linear Programming
Persamaan umum model linear programming dapat dituliskan sebagai berikut:
Optimalkan Z = c1x1 + c2x2 + … + cnxn
Terhadap kendala:
a11x1 + a12x2 + … + a1nxn ≤ b1
a21x1 + a22x2 + … + a2nxn ≤ b2
…
am1x1 + am2x2 + … + amnxn ≤ bm
x1, x2, …, xn ≥ 0
Dimana:
- Z adalah fungsi objektif yang ingin dioptimalkan (dimaksimalkan atau diminimalkan).
- c1, c2, …, cn adalah koefisien fungsi objektif.
- x1, x2, …, xn adalah variabel keputusan.
- aij adalah koefisien kendala.
- bi adalah nilai kanan kendala.
- m adalah jumlah kendala.
- n adalah jumlah variabel keputusan.
Perbedaan Fungsi Objektif dan Kendala
Fungsi objektif dan kendala merupakan bagian penting dalam model linear programming. Fungsi objektif menunjukkan tujuan yang ingin dicapai, sedangkan kendala menunjukkan batasan yang harus dipenuhi. Perbedaan utama antara fungsi objektif dan kendala adalah:
- Fungsi objektif adalah fungsi yang ingin dioptimalkan (dimaksimalkan atau diminimalkan), sedangkan kendala adalah batasan yang harus dipenuhi oleh solusi.
- Fungsi objektif biasanya hanya memiliki satu persamaan, sedangkan kendala dapat memiliki beberapa persamaan atau pertidaksamaan.
- Fungsi objektif biasanya dinyatakan dalam bentuk linier, sedangkan kendala dapat berupa fungsi linier atau non-linier.
Metode Penyelesaian Linear Programming
Linear programming merupakan teknik optimasi matematika yang digunakan untuk mencari solusi terbaik dari suatu masalah dengan batasan-batasan tertentu. Masalah ini biasanya melibatkan penentuan nilai variabel yang dapat memaksimalkan atau meminimalkan fungsi tujuan, yang merupakan fungsi linear dari variabel tersebut. Dalam prakteknya, linear programming banyak diaplikasikan di berbagai bidang, seperti manajemen produksi, keuangan, dan logistik.
Untuk menemukan solusi optimal dari masalah linear programming, terdapat beberapa metode yang dapat digunakan. Metode-metode ini memiliki kelebihan dan kekurangan masing-masing, sehingga pemilihan metode yang tepat bergantung pada karakteristik masalah yang dihadapi.
Metode Grafik
Metode grafik merupakan metode yang mudah dipahami dan diaplikasikan untuk masalah linear programming dengan dua variabel. Metode ini melibatkan plotting batasan masalah pada diagram Cartesian, kemudian menentukan titik-titik ekstrem (corner points) dari daerah yang memenuhi batasan. Solusi optimal terletak pada salah satu titik ekstrem tersebut, dan dapat ditentukan dengan mengevaluasi fungsi tujuan pada setiap titik ekstrem.
Contoh Soal:
Sebuah perusahaan memproduksi dua jenis produk, A dan B. Setiap produk memerlukan bahan baku dan waktu produksi yang berbeda, seperti yang ditunjukkan dalam tabel berikut:
| Produk | Bahan Baku (satuan) | Waktu Produksi (jam) |
|---|---|---|
| A | 2 | 3 |
| B | 3 | 2 |
Perusahaan memiliki persediaan bahan baku sebanyak 12 satuan dan waktu produksi maksimal 15 jam. Keuntungan per unit produk A adalah Rp 10.000 dan produk B adalah Rp 15.000. Berapakah jumlah produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan?
Langkah-langkah menyelesaikan masalah ini dengan metode grafik adalah:
- Tentukan fungsi tujuan. Fungsi tujuan dalam masalah ini adalah memaksimalkan keuntungan, yang dapat ditulis sebagai:
Keuntungan = 10.000A + 15.000B
- Tentukan batasan masalah. Batasan masalah ini adalah persediaan bahan baku dan waktu produksi yang tersedia.
2A + 3B ≤ 12 (Batasan bahan baku)
3A + 2B ≤ 15 (Batasan waktu produksi)
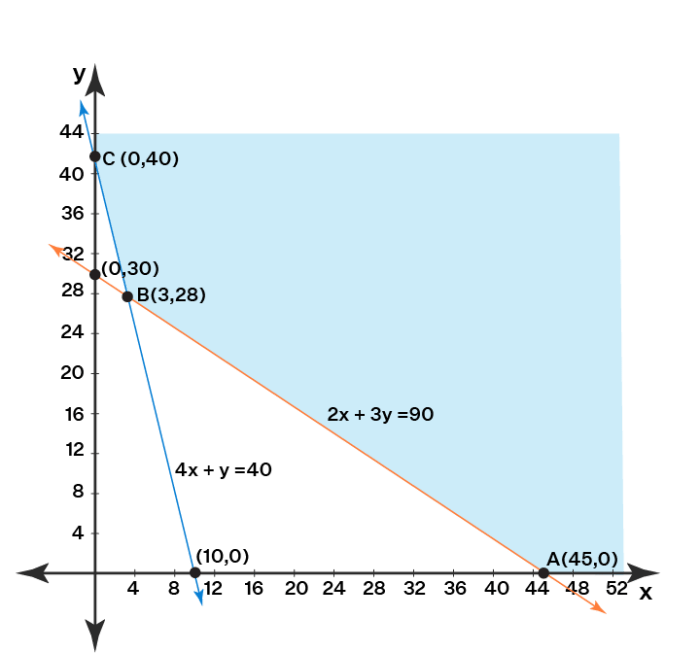
A ≥ 0, B ≥ 0 (Batasan non-negatif) - Plot batasan masalah pada diagram Cartesian. Untuk setiap batasan, kita dapat mengubahnya menjadi persamaan dan kemudian menentukan titik potong dengan sumbu x dan sumbu y. Misalnya, untuk batasan 2A + 3B ≤ 12, kita dapat mengubahnya menjadi 2A + 3B = 12. Titik potong dengan sumbu x diperoleh dengan menetapkan B = 0, sehingga A = 6. Titik potong dengan sumbu y diperoleh dengan menetapkan A = 0, sehingga B = 4.
Selanjutnya, hubungkan kedua titik potong tersebut untuk mendapatkan garis yang mewakili batasan tersebut. Lakukan hal yang sama untuk batasan lainnya. Daerah yang memenuhi semua batasan disebut daerah feasible (daerah layak).
- Tentukan titik-titik ekstrem dari daerah feasible. Titik-titik ekstrem adalah titik-titik sudut dari daerah feasible. Dalam contoh ini, terdapat empat titik ekstrem: (0,0), (0,4), (3,2), dan (5,0).
- Evaluasi fungsi tujuan pada setiap titik ekstrem.
Keuntungan pada (0,0) = 10.000(0) + 15.000(0) = 0
Keuntungan pada (0,4) = 10.000(0) + 15.000(4) = 60.000
Keuntungan pada (3,2) = 10.000(3) + 15.000(2) = 60.000
Keuntungan pada (5,0) = 10.000(5) + 15.000(0) = 50.000 - Tentukan solusi optimal. Solusi optimal adalah titik ekstrem yang menghasilkan nilai fungsi tujuan maksimal. Dalam contoh ini, titik (0,4) dan (3,2) menghasilkan keuntungan maksimal sebesar Rp 60.000. Artinya, perusahaan dapat memaksimalkan keuntungan dengan memproduksi 0 unit produk A dan 4 unit produk B, atau memproduksi 3 unit produk A dan 2 unit produk B.
Aplikasi Linear Programming
Linear programming (LP) adalah teknik optimasi matematika yang digunakan untuk mencari solusi terbaik untuk masalah yang melibatkan batasan dan tujuan yang terdefinisi dengan baik. LP memiliki banyak aplikasi praktis dalam berbagai bidang, termasuk bisnis, manufaktur, keuangan, dan kesehatan.
Contoh Kasus Nyata Penggunaan Linear Programming
Berikut adalah beberapa contoh kasus nyata yang menunjukkan bagaimana LP dapat digunakan untuk pengambilan keputusan dalam bidang bisnis:
- Manajemen Inventaris: LP dapat membantu perusahaan menentukan jumlah optimal produk yang harus disimpan di gudang untuk meminimalkan biaya penyimpanan dan menghindari kekurangan stok.
- Perencanaan Produksi: LP dapat digunakan untuk mengoptimalkan jadwal produksi, dengan mempertimbangkan batasan sumber daya seperti tenaga kerja, bahan baku, dan mesin, untuk memaksimalkan keuntungan atau meminimalkan biaya.
- Alokasi Iklan: LP dapat membantu perusahaan menentukan alokasi anggaran iklan yang optimal di berbagai media, dengan mempertimbangkan target pasar dan ROI (Return on Investment) yang diharapkan.
- Penjadwalan Karyawan: LP dapat digunakan untuk menyusun jadwal kerja karyawan yang optimal, dengan mempertimbangkan kebutuhan bisnis dan preferensi karyawan.
Merancang Model Linear Programming untuk Strategi Produksi Optimal
Perusahaan manufaktur dapat menggunakan LP untuk menentukan strategi produksi optimal yang memaksimalkan keuntungan atau meminimalkan biaya. Berikut adalah contoh model LP sederhana untuk perusahaan yang memproduksi dua jenis produk, A dan B:
- Tujuan: Memaksimalkan keuntungan total
- Variabel Keputusan:
- x: Jumlah unit produk A yang diproduksi
- y: Jumlah unit produk B yang diproduksi
- Fungsi Objektif: Keuntungan total = 5x + 8y (asumsi keuntungan per unit produk A adalah 5 dan produk B adalah 8)
- Kendala:
- Kendala bahan baku: 2x + 3y ≤ 120 (asumsi ketersediaan bahan baku maksimal 120 unit)
- Kendala tenaga kerja: x + y ≤ 60 (asumsi ketersediaan tenaga kerja maksimal 60 jam)
- Kendala non-negatif: x ≥ 0, y ≥ 0 (jumlah produk yang diproduksi tidak boleh negatif)
Model LP ini dapat dipecahkan menggunakan software LP seperti Excel Solver atau software khusus LP lainnya untuk mendapatkan solusi optimal, yaitu jumlah unit produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan total.
Mengoptimalkan Alokasi Sumber Daya dalam Sebuah Proyek
LP juga dapat digunakan untuk mengoptimalkan alokasi sumber daya dalam sebuah proyek. Misalnya, dalam proyek konstruksi, LP dapat digunakan untuk menentukan alokasi tenaga kerja, peralatan, dan bahan baku yang optimal untuk meminimalkan waktu penyelesaian proyek dan biaya.
Model LP untuk alokasi sumber daya dalam proyek konstruksi akan memiliki tujuan untuk meminimalkan waktu penyelesaian proyek atau biaya proyek. Variabel keputusan akan mencakup jumlah sumber daya yang dialokasikan untuk setiap aktivitas dalam proyek. Kendala akan mencakup keterbatasan sumber daya, ketergantungan aktivitas, dan batasan waktu.
Dengan menggunakan LP, manajer proyek dapat menentukan alokasi sumber daya yang optimal untuk meminimalkan waktu penyelesaian proyek dan biaya, serta meningkatkan efisiensi proyek secara keseluruhan.
Contoh Soal Linear Programming
Linear programming adalah teknik optimasi matematika yang digunakan untuk menemukan solusi terbaik untuk masalah yang melibatkan pembatasan sumber daya dan tujuan yang ingin dicapai. Dalam konteks bisnis, linear programming dapat diterapkan untuk berbagai keperluan, seperti pengalokasian sumber daya, penjadwalan produksi, dan optimasi keuntungan. Salah satu contoh penerapan linear programming yang umum adalah pengaturan produksi, di mana perusahaan ingin memaksimalkan keuntungan dengan memaksimalkan produksi dengan kendala bahan baku dan waktu produksi yang terbatas.
Contoh Soal Linear Programming dengan Tema “Pengaturan Produksi”
Sebuah perusahaan memproduksi dua jenis produk, yaitu produk A dan produk B. Produk A membutuhkan 2 kg bahan baku dan 1 jam waktu produksi, sedangkan produk B membutuhkan 1 kg bahan baku dan 2 jam waktu produksi. Perusahaan memiliki 10 kg bahan baku dan 8 jam waktu produksi yang tersedia. Keuntungan yang diperoleh dari penjualan produk A adalah Rp10.000 per unit, sedangkan keuntungan produk B adalah Rp15.000 per unit. Berapa banyak unit produk A dan produk B yang harus diproduksi agar keuntungan perusahaan maksimal?
Contoh soal linear programming biasanya melibatkan mencari nilai optimal (maksimum atau minimum) dari suatu fungsi objektif dengan batasan-batasan tertentu. Nah, untuk memahami konsep ini, kita perlu menguasai persamaan linear terlebih dahulu, termasuk persamaan linear tiga variabel yang sering dipelajari di kelas 10.
Kamu bisa menemukan contoh soal persamaan linear tiga variabel kelas 10 di situs ini. Setelah memahami persamaan linear, kamu akan lebih siap untuk mempelajari dan menyelesaikan contoh soal linear programming.
Langkah-langkah Penyelesaian Soal Linear Programming Menggunakan Metode Simplex
Untuk menyelesaikan soal linear programming dengan metode simplex, kita perlu merumuskan masalah tersebut dalam bentuk model matematika. Model matematika tersebut terdiri dari:
- Fungsi tujuan: Fungsi yang ingin dioptimalkan, dalam kasus ini adalah keuntungan.
- Kendala: Batasan sumber daya yang tersedia, seperti bahan baku dan waktu produksi.
- Variabel keputusan: Jumlah produk yang akan diproduksi, dalam kasus ini adalah jumlah produk A dan produk B.
Berikut adalah langkah-langkah penyelesaian soal linear programming menggunakan metode simplex:
- Rumuskan masalah dalam bentuk model matematika.
Misalkan:
- x = Jumlah produk A yang diproduksi
- y = Jumlah produk B yang diproduksi
Fungsi tujuan (maksimalkan keuntungan):
Z = 10.000x + 15.000y
Kendala:
- 2x + y ≤ 10 (Kendala bahan baku)
- x + 2y ≤ 8 (Kendala waktu produksi)
- x ≥ 0, y ≥ 0 (Kendala non-negatif)
- Ubah kendala menjadi persamaan dengan menambahkan variabel slack.
Kendala bahan baku:
2x + y + s1 = 10
Kendala waktu produksi:
x + 2y + s2 = 8
Variabel slack (s1 dan s2) merupakan variabel tambahan yang mewakili sisa bahan baku dan waktu produksi yang tidak digunakan.
- Buat tabel simplex awal.
Tabel simplex awal berisi koefisien dari fungsi tujuan dan kendala, serta nilai variabel slack.
Basis x y s1 s2 RHS s1 2 1 1 0 10 s2 1 2 0 1 8 Z -10.000 -15.000 0 0 0 RHS (Right Hand Side) merupakan nilai konstan pada kendala.
- Pilih kolom pivot.
Kolom pivot adalah kolom dengan nilai koefisien paling negatif pada baris Z. Dalam tabel ini, kolom pivot adalah kolom x (-10.000).
- Pilih baris pivot.
Baris pivot adalah baris dengan nilai rasio RHS terhadap koefisien kolom pivot terkecil. Dalam tabel ini, baris pivot adalah baris s1 (10/2 = 5).
- Buat elemen pivot menjadi 1.
Bagi baris pivot dengan nilai elemen pivot (2).
Basis x y s1 s2 RHS x 1 1/2 1/2 0 5 s2 1 2 0 1 8 Z -10.000 -15.000 0 0 0 - Buat elemen lain pada kolom pivot menjadi 0.
Kurangi baris s2 dengan baris x yang dikalikan dengan 1.
Basis x y s1 s2 RHS x 1 1/2 1/2 0 5 s2 0 3/2 -1/2 1 3 Z -10.000 -15.000 0 0 0 - Ubah nilai Z.
Tambahkan baris Z dengan baris x yang dikalikan dengan 10.000.
Basis x y s1 s2 RHS x 1 1/2 1/2 0 5 s2 0 3/2 -1/2 1 3 Z 0 -10.000 5.000 0 50.000 - Ulangi langkah 4-8 hingga semua nilai pada baris Z tidak negatif.
Dalam tabel ini, kolom pivot adalah kolom y (-10.000). Baris pivot adalah baris s2 (3/(3/2) = 2).
Setelah melakukan operasi baris, tabel simplex menjadi:
Basis x y s1 s2 RHS x 1 0 2/3 -1/3 4 y 0 1 -1/3 2/3 2 Z 0 0 10.000/3 20.000/3 110.000 Semua nilai pada baris Z sudah tidak negatif, sehingga solusi optimal telah ditemukan.
- Interpretasi solusi optimal.
Solusi optimal menunjukkan bahwa perusahaan harus memproduksi 4 unit produk A dan 2 unit produk B untuk memaksimalkan keuntungan. Keuntungan maksimal yang dapat dicapai adalah Rp110.000.
Tabel Hasil Perhitungan dan Interpretasi Solusi Optimal
| Variabel | Nilai Optimal | Interpretasi |
|---|---|---|
| x (Produk A) | 4 | Jumlah produk A yang diproduksi adalah 4 unit. |
| y (Produk B) | 2 | Jumlah produk B yang diproduksi adalah 2 unit. |
| Z (Keuntungan) | 110.000 | Keuntungan maksimal yang dapat dicapai adalah Rp110.000. |
Permasalahan dalam Linear Programming
Linear programming, meskipun merupakan alat yang ampuh untuk pengambilan keputusan, memiliki beberapa kendala dan batasan dalam penerapannya. Penting untuk memahami batasan ini agar dapat menginterpretasikan hasil solusi linear programming secara akurat dan mengambil keputusan yang tepat.
Kendala dan Batasan dalam Linear Programming
Beberapa kendala dan batasan yang umum dijumpai dalam penerapan linear programming meliputi:
- Asumsi Linearitas: Linear programming mengasumsikan bahwa hubungan antara variabel dan fungsi tujuan adalah linier. Dalam praktiknya, banyak situasi yang melibatkan hubungan non-linear, yang dapat menyebabkan hasil solusi yang tidak akurat.
- Data yang Tepat: Linear programming sangat bergantung pada data yang akurat. Kesalahan atau ketidakpastian dalam data dapat memengaruhi hasil solusi.
- Kompleksitas Masalah: Masalah linear programming yang kompleks dengan banyak variabel dan kendala dapat sulit untuk dimodelkan dan diselesaikan.
- Interpretasi Solusi: Solusi optimal yang dihasilkan oleh linear programming mungkin tidak selalu praktis atau layak dalam konteks dunia nyata.
Dampak Ketidakpastian Data
Ketidakpastian dalam data dapat memengaruhi hasil solusi linear programming dengan berbagai cara:
- Solusi yang Tidak Akurat: Data yang tidak akurat dapat menyebabkan solusi optimal yang tidak realistis atau tidak dapat dicapai.
- Kesalahan dalam Pengambilan Keputusan: Keputusan yang diambil berdasarkan solusi yang didasarkan pada data yang tidak akurat dapat mengakibatkan kerugian finansial atau operasional.
- Peningkatan Risiko: Ketidakpastian dalam data dapat meningkatkan risiko kegagalan dalam mencapai tujuan yang diinginkan.
Solusi Alternatif untuk Mengatasi Kendala
| Kendala | Solusi Alternatif |
|---|---|
| Asumsi Linearitas | – Menggunakan model non-linear – Menggunakan teknik linearisasi untuk mendekati hubungan non-linear |
| Data yang Tepat | – Meningkatkan kualitas data melalui pengumpulan dan verifikasi yang lebih baik – Menggunakan teknik analisis sensitivitas untuk mengevaluasi dampak perubahan data pada solusi |
| Kompleksitas Masalah | – Menggunakan algoritma heuristik untuk menemukan solusi yang layak – Memecah masalah kompleks menjadi sub-masalah yang lebih kecil |
| Interpretasi Solusi | – Melibatkan para ahli di bidang terkait untuk menilai solusi optimal – Melakukan analisis sensitivitas untuk mengevaluasi dampak perubahan parameter pada solusi |
Perkembangan Linear Programming: Contoh Soal Linear Programming
Linear programming (LP) merupakan salah satu metode optimasi yang telah banyak digunakan dalam berbagai bidang, mulai dari bisnis dan manufaktur hingga transportasi dan keuangan. Metode ini telah berkembang pesat sejak kemunculannya, dengan berbagai inovasi dan pengembangan yang semakin meningkatkan kemampuannya dalam menyelesaikan masalah optimasi kompleks.
Sejarah Awal dan Evolusi Metode Linear Programming
Linear programming pertama kali muncul pada tahun 1940-an, di tengah Perang Dunia II. George B. Dantzig, seorang ahli matematika Amerika, mengembangkan metode Simplex untuk menyelesaikan masalah optimasi linear. Metode ini memungkinkan pengambilan keputusan optimal dengan mempertimbangkan berbagai batasan dan persyaratan. Metode Simplex merupakan dasar dari linear programming modern dan telah digunakan secara luas dalam berbagai aplikasi.
Seiring perkembangan teknologi komputer, metode linear programming semakin berkembang dan semakin mudah diterapkan. Metode Simplex menjadi lebih efisien dan mampu menangani masalah yang lebih besar dan kompleks. Selain itu, berbagai metode lain seperti metode interior point dan metode dual simplex juga dikembangkan untuk mengatasi keterbatasan metode Simplex.
Aplikasi Baru dan Canggih Linear Programming di Era Teknologi Informasi
Di era teknologi informasi, linear programming telah menemukan aplikasi baru yang lebih canggih dan luas. Kemampuannya dalam menyelesaikan masalah optimasi kompleks telah membuka peluang baru di berbagai bidang.
- Manajemen Rantai Pasokan: Linear programming dapat digunakan untuk mengoptimalkan alur rantai pasokan, mulai dari pengadaan bahan baku hingga distribusi produk akhir. Hal ini dapat membantu perusahaan untuk meminimalkan biaya, meningkatkan efisiensi, dan memaksimalkan keuntungan.
- Pemrograman Keuangan: Linear programming dapat digunakan untuk memaksimalkan keuntungan investasi, meminimalkan risiko, dan mengelola portofolio investasi dengan lebih efektif.
- Optimasi Logistik: Linear programming dapat digunakan untuk merancang rute pengiriman yang optimal, meminimalkan waktu dan biaya pengiriman, serta memaksimalkan efisiensi logistik.
- Kecerdasan Buatan (AI): Linear programming merupakan bagian integral dari algoritma pembelajaran mesin dalam AI. Metode ini digunakan untuk menyelesaikan masalah optimasi dalam berbagai aplikasi AI, seperti pengenalan pola, klasifikasi data, dan pengambilan keputusan.
Potensi dan Tantangan Linear Programming di Masa Depan
Linear programming memiliki potensi besar untuk berkembang di masa depan, seiring dengan perkembangan teknologi dan kebutuhan baru dalam berbagai bidang. Berikut adalah beberapa potensi dan tantangan yang dihadapi linear programming di masa depan:
- Peningkatan Skalabilitas: Seiring dengan meningkatnya kompleksitas masalah yang dihadapi, linear programming perlu terus dikembangkan untuk menangani masalah dengan skala yang lebih besar.
- Integrasi dengan Teknologi Lain: Linear programming dapat diintegrasikan dengan teknologi lain seperti big data, cloud computing, dan internet of things (IoT) untuk meningkatkan kemampuannya dalam menyelesaikan masalah yang lebih kompleks.
- Pengembangan Metode Baru: Pengembangan metode baru yang lebih efisien dan efektif untuk menyelesaikan masalah optimasi linear akan terus menjadi fokus utama di masa depan.
- Tantangan dalam Penerapan: Penerapan linear programming dalam dunia nyata seringkali menghadapi tantangan, seperti data yang tidak lengkap, ketidakpastian, dan kompleksitas masalah yang sulit dimodelkan.
Software Linear Programming
Linear programming adalah metode matematis yang digunakan untuk mengoptimalkan suatu fungsi tujuan (objective function) dengan batasan (constraints) yang berbentuk linear. Dalam praktiknya, linear programming banyak digunakan untuk menyelesaikan masalah optimasi dalam berbagai bidang, seperti ekonomi, manajemen, dan rekayasa. Untuk membantu dalam menyelesaikan masalah linear programming, tersedia beberapa software yang dapat membantu dalam proses perhitungan dan analisis.
Contoh Software Linear Programming
Berikut adalah beberapa contoh software yang dapat digunakan untuk menyelesaikan masalah linear programming:
- Solver dalam Microsoft Excel: Solver merupakan add-in yang tersedia di Microsoft Excel. Solver dapat digunakan untuk menyelesaikan masalah linear programming dengan berbagai metode, seperti Simplex, Evolutionary, dan GRG Nonlinear. Solver dapat digunakan untuk mengoptimalkan fungsi tujuan dengan batasan yang berbentuk linear, non-linear, dan integer.
- IBM ILOG CPLEX: IBM ILOG CPLEX merupakan software komersial yang dirancang untuk menyelesaikan masalah optimasi linear dan integer. CPLEX memiliki kemampuan untuk menyelesaikan masalah linear programming dengan skala besar dan kompleks. Software ini juga menyediakan berbagai fitur untuk analisis sensitivitas dan visualisasi solusi.
- Gurobi Optimizer: Gurobi Optimizer merupakan software komersial lain yang dirancang untuk menyelesaikan masalah optimasi linear dan integer. Gurobi Optimizer dikenal dengan kemampuannya dalam menyelesaikan masalah dengan kecepatan tinggi dan akurasi yang tinggi. Software ini juga menyediakan berbagai fitur untuk analisis sensitivitas dan visualisasi solusi.
- OpenSolver: OpenSolver merupakan add-in gratis untuk Microsoft Excel. OpenSolver dapat digunakan untuk menyelesaikan masalah linear programming dengan metode Simplex. OpenSolver merupakan pilihan yang baik untuk pengguna yang ingin mencoba menggunakan software linear programming tanpa harus mengeluarkan biaya.
- R Programming Language: R merupakan bahasa pemrograman yang populer untuk analisis data dan statistika. R memiliki beberapa paket yang dapat digunakan untuk menyelesaikan masalah linear programming, seperti lpSolve, Rglpk, dan linprog. Paket-paket ini memungkinkan pengguna untuk menyelesaikan masalah linear programming dengan menggunakan kode R.
Fitur dan Keunggulan Software Linear Programming, Contoh soal linear programming
Software linear programming memiliki beberapa fitur dan keunggulan yang dapat membantu dalam menyelesaikan masalah optimasi:
- Kemudahan Penggunaan: Software linear programming dirancang dengan antarmuka yang mudah digunakan, sehingga pengguna dapat dengan mudah memasukkan data dan menentukan fungsi tujuan dan batasan. Software ini juga menyediakan berbagai fitur untuk membantu pengguna dalam memahami dan menganalisis solusi.
- Kecepatan dan Akurasi: Software linear programming dapat menyelesaikan masalah linear programming dengan kecepatan tinggi dan akurasi yang tinggi. Software ini menggunakan algoritma yang canggih untuk menemukan solusi optimal dalam waktu yang relatif singkat.
- Analisis Sensitivitas: Software linear programming memungkinkan pengguna untuk melakukan analisis sensitivitas. Analisis sensitivitas dapat membantu pengguna untuk memahami bagaimana perubahan dalam data atau batasan dapat mempengaruhi solusi optimal.
- Visualisasi Solusi: Software linear programming menyediakan berbagai fitur untuk visualisasi solusi. Visualisasi solusi dapat membantu pengguna untuk memahami solusi optimal dengan lebih baik dan membuat keputusan yang lebih baik.
Contoh Penggunaan Software Linear Programming
Berikut adalah contoh penggunaan software linear programming untuk menyelesaikan masalah linear programming yang kompleks:
Sebuah perusahaan manufaktur ingin menentukan jumlah produk A dan produk B yang harus diproduksi untuk memaksimalkan keuntungan. Perusahaan memiliki batasan pada jumlah bahan baku yang tersedia dan waktu produksi. Fungsi tujuan adalah untuk memaksimalkan keuntungan, sedangkan batasannya adalah jumlah bahan baku yang tersedia dan waktu produksi. Software linear programming dapat digunakan untuk menentukan jumlah produk A dan produk B yang harus diproduksi untuk memaksimalkan keuntungan dengan mempertimbangkan batasan yang ada.
Software linear programming akan membantu perusahaan dalam menentukan solusi optimal dengan mempertimbangkan semua batasan dan fungsi tujuan. Software ini juga dapat digunakan untuk melakukan analisis sensitivitas untuk melihat bagaimana perubahan dalam batasan atau fungsi tujuan dapat mempengaruhi solusi optimal.
Kesimpulan
Linear programming merupakan metode optimasi matematika yang membantu menemukan solusi terbaik untuk masalah yang melibatkan pembatasan dan tujuan tertentu. Metode ini melibatkan penggunaan fungsi linear untuk memodelkan batasan dan tujuan, dan algoritma untuk menemukan titik optimal yang memenuhi batasan dan memaksimalkan atau meminimalkan tujuan.
Pentingnya Memahami Linear Programming
Linear programming memiliki aplikasi luas dalam berbagai bidang, seperti:
- Manajemen Bisnis: Membantu perusahaan dalam pengambilan keputusan terkait alokasi sumber daya, penjadwalan produksi, dan optimalisasi profit.
- Manajemen Operasional: Digunakan untuk meminimalkan biaya produksi, memaksimalkan efisiensi, dan mengoptimalkan penggunaan sumber daya.
- Manajemen Keuangan: Membantu dalam pengambilan keputusan terkait investasi, manajemen portofolio, dan perencanaan keuangan.
- Ilmu Komputer: Digunakan dalam pengembangan algoritma, optimasi jaringan, dan analisis data.
- Ilmu Sosial: Digunakan dalam model ekonomi, perencanaan sosial, dan analisis politik.
Rekomendasi untuk Mempelajari Lebih Lanjut
Bagi Anda yang ingin mempelajari lebih lanjut tentang linear programming, berikut beberapa saran:
- Pelajari konsep dasar matematika: Pemahaman yang kuat tentang aljabar linear, kalkulus, dan teori himpunan sangat penting.
- Baca buku dan artikel tentang linear programming: Banyak sumber daya yang tersedia, baik secara online maupun offline, yang dapat membantu Anda mempelajari konsep-konsep dasar dan aplikasi linear programming.
- Ikuti kursus atau workshop: Kursus dan workshop dapat memberikan pemahaman yang lebih mendalam dan praktis tentang linear programming.
- Berlatih dengan contoh soal: Melalui latihan, Anda dapat mengasah pemahaman dan kemampuan Anda dalam menyelesaikan masalah linear programming.
- Manfaatkan software linear programming: Software seperti Excel Solver, MATLAB, dan R dapat membantu Anda dalam menyelesaikan masalah linear programming dengan lebih mudah dan efisien.
Penutupan Akhir
Linear programming adalah alat yang sangat bermanfaat dalam berbagai bidang, mulai dari bisnis, ekonomi, hingga ilmu komputer. Memahami konsep dasar linear programming dan kemampuan untuk menyelesaikan contoh soal akan memperkaya pengetahuan dan keterampilan Anda dalam menghadapi masalah pengambilan keputusan yang kompleks. Dengan mempelajari lebih lanjut tentang linear programming, Anda dapat menjadi pengambil keputusan yang lebih strategis dan efisien.