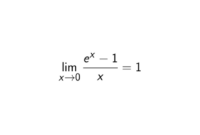Contoh Soal Limit Fungsi Trigonometri Tak Hingga: Pelajari dan Kuasai Konsepnya

Contoh soal limit fungsi trigonometri tak hingga – Menjelajahi dunia matematika, kita seringkali menemukan konsep limit yang menarik, terutama dalam konteks fungsi trigonometri. Limit fungsi trigonometri tak hingga, khususnya, membuka jalan untuk memahami bagaimana perilaku fungsi trigonometri ketika variabelnya mendekati nilai tak hingga. Konsep ini mendasari banyak aplikasi di berbagai bidang, seperti fisika, teknik, dan ekonomi.

Dalam artikel ini, kita akan menyelami dunia limit fungsi trigonometri tak hingga dengan membahas pengertian, sifat, teknik penyelesaian, contoh soal, dan penerapannya dalam kehidupan nyata. Siap untuk memahami konsep ini dengan lebih dalam? Mari kita mulai!

Pengertian Limit Fungsi Trigonometri Tak Hingga

Limit fungsi trigonometri tak hingga merupakan konsep penting dalam kalkulus yang mengkaji perilaku fungsi trigonometri ketika variabel bebasnya mendekati nilai tak hingga. Pada dasarnya, kita ingin mengetahui nilai yang didekati oleh fungsi trigonometri tersebut saat variabel bebasnya semakin besar atau semakin kecil tanpa batas.

Contoh Limit Fungsi Trigonometri Tak Hingga

Untuk memahami konsep limit fungsi trigonometri tak hingga, mari kita bahas contoh berikut:

Tentukan limit dari fungsi sin(x)/x ketika x mendekati tak hingga.

Untuk menyelesaikannya, kita dapat menggunakan beberapa metode, seperti:

1. Metode grafik: Dengan melihat grafik fungsi sin(x)/x, kita dapat melihat bahwa ketika x semakin besar, nilai fungsi mendekati 0.
2. Metode teorema limit: Teorema limit menyatakan bahwa jika f(x) dan g(x) adalah fungsi yang kontinu dan g(x) tidak sama dengan 0, maka limit dari f(x)/g(x) ketika x mendekati tak hingga sama dengan limit dari f(x) dibagi limit dari g(x) ketika x mendekati tak hingga. Dalam kasus ini, limit dari sin(x) ketika x mendekati tak hingga adalah antara -1 dan 1, sedangkan limit dari x ketika x mendekati tak hingga adalah tak hingga. Oleh karena itu, limit dari sin(x)/x ketika x mendekati tak hingga adalah 0.

Tabel Limit Fungsi Trigonometri Tak Hingga

Berikut adalah beberapa contoh limit fungsi trigonometri tak hingga dengan hasil limit yang berbeda-beda:

Fungsi	Limit ketika x mendekati tak hingga
sin(x)/x	0
cos(x)/x	0
tan(x)/x	0
cot(x)/x	0
sec(x)/x	0
csc(x)/x	0

Sifat-Sifat Limit Fungsi Trigonometri Tak Hingga

Limit fungsi trigonometri tak hingga adalah konsep penting dalam kalkulus. Memahami sifat-sifatnya memungkinkan kita untuk menyelesaikan masalah limit yang melibatkan fungsi trigonometri dan variabel yang menuju tak hingga.

Sifat-sifat ini membantu kita untuk memahami bagaimana fungsi trigonometri berperilaku ketika variabelnya semakin besar atau kecil.

Sifat-Sifat Limit Fungsi Trigonometri Tak Hingga

Beberapa sifat penting dari limit fungsi trigonometri tak hingga adalah:

• Limit Fungsi Sinus dan Kosinus: Limit dari fungsi sinus dan kosinus ketika variabelnya menuju tak hingga tidak ada. Ini karena nilai sinus dan kosinus berosilasi antara -1 dan 1.
• Limit Fungsi Tangent dan Kotangent: Limit dari fungsi tangent dan kotangent ketika variabelnya menuju tak hingga tidak ada. Ini karena nilai tangent dan kotangent dapat mencapai nilai tak hingga ketika variabelnya mendekati titik-titik tertentu.
• Limit Fungsi Sekan dan Kosekan: Limit dari fungsi sekan dan kosekan ketika variabelnya menuju tak hingga tidak ada. Ini karena nilai sekan dan kosekan dapat mencapai nilai tak hingga ketika variabelnya mendekati titik-titik tertentu.

Contoh Penerapan Sifat-Sifat Limit Fungsi Trigonometri Tak Hingga

Misalnya, perhatikan limit berikut:

lim_x→∞ sin(x)

Karena nilai sinus berosilasi antara -1 dan 1, limit ini tidak ada.

Contoh lainnya, perhatikan limit berikut:

lim_x→∞ tan(x)

Mencari contoh soal limit fungsi trigonometri tak hingga? Keren! Kamu bisa mulai dengan memahami konsep dasar limit fungsi dan bagaimana cara mengaplikasikannya pada fungsi trigonometri. Untuk latihan lebih lanjut, kamu bisa cek contoh soal fungsi kelas 11 di sini , yang membahas berbagai jenis fungsi, termasuk fungsi linear, kuadrat, dan eksponen.

Dengan latihan yang cukup, kamu pasti bisa menguasai konsep limit fungsi trigonometri tak hingga dengan mudah!

Karena nilai tangent dapat mencapai nilai tak hingga ketika variabelnya mendekati titik-titik tertentu, limit ini juga tidak ada.

Ringkasan Sifat-Sifat Limit Fungsi Trigonometri Tak Hingga

Limit fungsi trigonometri tak hingga dapat tidak ada, terutama untuk fungsi sinus, kosinus, tangent, kotangent, sekan, dan kosekan. Hal ini karena nilai fungsi trigonometri tersebut dapat berosilasi atau mencapai nilai tak hingga ketika variabelnya menuju tak hingga.

Teknik Penyelesaian Limit Fungsi Trigonometri Tak Hingga

Limit fungsi trigonometri tak hingga merupakan konsep penting dalam kalkulus yang melibatkan penentuan nilai fungsi trigonometri saat variabel mendekati tak hingga. Untuk menyelesaikan limit fungsi trigonometri tak hingga, beberapa teknik dapat diterapkan. Berikut ini akan dibahas beberapa teknik umum yang sering digunakan, dilengkapi dengan contoh penerapannya.

Manipulasi Aljabar

Teknik manipulasi aljabar melibatkan pengubahan bentuk fungsi trigonometri dengan menggunakan sifat-sifat aljabar dan identitas trigonometri. Tujuannya adalah untuk menyederhanakan fungsi dan membuat proses pencarian limit lebih mudah.

• Bagi pembilang dan penyebut dengan pangkat tertinggi x.
• Gunakan identitas trigonometri untuk mengubah bentuk fungsi.
• Faktorkan ekspresi aljabar.

Sebagai contoh, perhatikan limit berikut:

lim_x→∞ (sin(x)/x)

Dengan membagi pembilang dan penyebut dengan x, kita mendapatkan:

lim_x→∞ (sin(x)/x) = lim_x→∞ (sin(x)/x) * (1/x) / (1/x) = lim_x→∞ (sin(x)/x²)

Karena |sin(x)| ≤ 1 untuk semua x, maka:

|sin(x)/x²| ≤ 1/x²

Ketika x mendekati tak hingga, 1/x² mendekati 0. Oleh karena itu, berdasarkan teorema sandwich, limit dari sin(x)/x² saat x mendekati tak hingga adalah 0.

Substitusi

Teknik substitusi melibatkan penggantian variabel dengan nilai yang mendekati tak hingga. Teknik ini hanya berlaku untuk fungsi yang kontinu di titik tak hingga.

• Gunakan substitusi untuk mengubah fungsi menjadi bentuk yang lebih sederhana.
• Evaluasi limit dari fungsi yang telah diubah.

Sebagai contoh, perhatikan limit berikut:

lim_x→∞ (cos(1/x))

Dengan mensubstitusikan y = 1/x, maka x = 1/y. Ketika x mendekati tak hingga, y mendekati 0. Dengan demikian, kita dapat menulis:

lim_x→∞ (cos(1/x)) = lim_y→0 (cos(y)) = cos(0) = 1

Penggunaan Identitas Trigonometri

Teknik ini melibatkan penggunaan identitas trigonometri untuk mengubah bentuk fungsi trigonometri menjadi bentuk yang lebih mudah diselesaikan.

• Identitas trigonometri dapat digunakan untuk menyederhanakan fungsi.
• Gunakan identitas trigonometri yang sesuai untuk mengubah bentuk fungsi.

Sebagai contoh, perhatikan limit berikut:

lim_x→∞ (tan(x)/x)

Dengan menggunakan identitas trigonometri tan(x) = sin(x)/cos(x), kita dapat menulis:

lim_x→∞ (tan(x)/x) = lim_x→∞ (sin(x)/cos(x) * 1/x) = lim_x→∞ (sin(x)/(x*cos(x)))

Karena |sin(x)| ≤ 1 dan |cos(x)| ≤ 1 untuk semua x, maka:

|sin(x)/(x*cos(x))| ≤ 1/x

Ketika x mendekati tak hingga, 1/x mendekati 0. Oleh karena itu, berdasarkan teorema sandwich, limit dari sin(x)/(x*cos(x)) saat x mendekati tak hingga adalah 0.

Tabel Ringkasan Teknik Penyelesaian Limit Fungsi Trigonometri Tak Hingga

Teknik	Contoh Penerapan
Manipulasi Aljabar	limx→∞ (sin(x)/x) = 0
Substitusi	limx→∞ (cos(1/x)) = 1
Penggunaan Identitas Trigonometri	limx→∞ (tan(x)/x) = 0

Penerapan Limit Fungsi Trigonometri Tak Hingga dalam Konteks Nyata

Limit fungsi trigonometri tak hingga memiliki aplikasi yang luas dalam berbagai bidang, membantu kita memahami perilaku fungsi trigonometri ketika variabel independen mendekati nilai tak hingga. Penerapannya dapat ditemukan dalam fisika, teknik, dan ekonomi, di mana konsep ini membantu kita dalam menganalisis fenomena periodik, gelombang, dan osilasi.

Penerapan dalam Fisika

Limit fungsi trigonometri tak hingga berperan penting dalam memahami perilaku gelombang dan osilasi dalam fisika. Konsep ini membantu kita dalam menganalisis gerakan periodik seperti gelombang suara, gelombang cahaya, dan gelombang elektromagnetik.

• Contohnya, dalam analisis gelombang suara, limit fungsi trigonometri tak hingga membantu kita dalam menentukan frekuensi dan amplitudo gelombang suara. Dengan menggunakan limit, kita dapat menentukan bagaimana amplitudo gelombang suara berubah seiring waktu.
• Dalam fisika gelombang, konsep limit fungsi trigonometri tak hingga digunakan untuk memahami perilaku gelombang cahaya. Limit membantu kita dalam menentukan panjang gelombang dan frekuensi cahaya, yang menentukan warna cahaya yang kita lihat.

Penerapan dalam Teknik

Limit fungsi trigonometri tak hingga memiliki aplikasi yang luas dalam berbagai bidang teknik, terutama dalam bidang sinyal dan sistem, elektronik, dan mekanika.

• Dalam bidang sinyal dan sistem, limit fungsi trigonometri tak hingga membantu kita dalam menganalisis sinyal periodik, seperti sinyal audio dan sinyal video. Limit membantu kita dalam menentukan frekuensi dan amplitudo sinyal, yang penting untuk memahami dan memproses sinyal tersebut.
• Dalam elektronik, limit fungsi trigonometri tak hingga digunakan untuk menganalisis rangkaian listrik AC. Limit membantu kita dalam menentukan impedansi dan fase rangkaian, yang penting untuk memahami perilaku rangkaian dan merancang sistem elektronik yang efisien.
• Dalam mekanika, limit fungsi trigonometri tak hingga digunakan untuk menganalisis gerakan periodik seperti getaran dan osilasi. Limit membantu kita dalam menentukan frekuensi dan amplitudo gerakan, yang penting untuk memahami perilaku sistem mekanik dan merancang sistem yang aman dan stabil.

Penerapan dalam Ekonomi

Limit fungsi trigonometri tak hingga juga memiliki aplikasi dalam ekonomi, terutama dalam bidang keuangan dan ekonomi makro.

• Dalam keuangan, limit fungsi trigonometri tak hingga digunakan untuk menganalisis pasar saham dan aset keuangan lainnya. Limit membantu kita dalam memahami perilaku harga aset dan meramalkan tren pasar.
• Dalam ekonomi makro, limit fungsi trigonometri tak hingga digunakan untuk menganalisis siklus bisnis dan pertumbuhan ekonomi. Limit membantu kita dalam memahami perilaku ekonomi makro dan meramalkan tren ekonomi.

Soal-Soal Latihan Limit Fungsi Trigonometri Tak Hingga

Setelah mempelajari konsep dasar limit fungsi trigonometri tak hingga, sekarang saatnya untuk mengasah kemampuanmu dengan mengerjakan soal-soal latihan. Soal-soal berikut ini disusun dengan tingkat kesulitan yang bervariasi, mulai dari yang mudah hingga yang menantang. Selesaikan setiap soal dengan cermat dan pahami langkah-langkah penyelesaiannya.

Contoh Soal Latihan

Berikut adalah lima contoh soal latihan limit fungsi trigonometri tak hingga beserta langkah penyelesaiannya:

1. Tentukan nilai dari

   lim_x→∞ sin(x)/x

   Langkah penyelesaian:

   1. Perhatikan bahwa fungsi sin(x) memiliki nilai yang terbatas, yaitu antara -1 dan 1, untuk setiap nilai x.

   2. Sementara itu, fungsi x akan terus bertambah besar tanpa batas saat x mendekati tak hingga.

   3. Oleh karena itu, nilai dari sin(x)/x akan semakin kecil dan mendekati nol saat x mendekati tak hingga.

   Jadi, nilai dari

   lim_x→∞ sin(x)/x = 0

2. Tentukan nilai dari

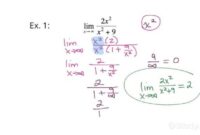
   lim_x→∞ (1 + cos(x))/x

   Langkah penyelesaian:

   1. Perhatikan bahwa fungsi cos(x) memiliki nilai yang terbatas, yaitu antara -1 dan 1, untuk setiap nilai x.

   2. Oleh karena itu, fungsi (1 + cos(x)) juga memiliki nilai yang terbatas, yaitu antara 0 dan 2, untuk setiap nilai x.

   3. Sementara itu, fungsi x akan terus bertambah besar tanpa batas saat x mendekati tak hingga.

   4. Oleh karena itu, nilai dari (1 + cos(x))/x akan semakin kecil dan mendekati nol saat x mendekati tak hingga.

   Jadi, nilai dari

   lim_x→∞ (1 + cos(x))/x = 0

3. Tentukan nilai dari

   lim_x→∞ (sin(x) + cos(x))/x

   Langkah penyelesaian:

   1. Perhatikan bahwa fungsi sin(x) dan cos(x) memiliki nilai yang terbatas, yaitu antara -1 dan 1, untuk setiap nilai x.

   2. Oleh karena itu, fungsi (sin(x) + cos(x)) juga memiliki nilai yang terbatas, yaitu antara -2 dan 2, untuk setiap nilai x.

   3. Sementara itu, fungsi x akan terus bertambah besar tanpa batas saat x mendekati tak hingga.

   4. Oleh karena itu, nilai dari (sin(x) + cos(x))/x akan semakin kecil dan mendekati nol saat x mendekati tak hingga.

   Jadi, nilai dari

   lim_x→∞ (sin(x) + cos(x))/x = 0

4. Tentukan nilai dari

   lim_x→∞ tan(x)/x

   Langkah penyelesaian:

   1. Perhatikan bahwa fungsi tan(x) memiliki nilai yang tidak terbatas saat x mendekati π/2 + kπ, di mana k adalah bilangan bulat.

   2. Oleh karena itu, fungsi tan(x)/x tidak memiliki limit yang pasti saat x mendekati tak hingga.

   Jadi, nilai dari

   lim_x→∞ tan(x)/x tidak ada

5. Tentukan nilai dari

   lim_x→∞ (sin(x) + 1)/x

   Langkah penyelesaian:

   1. Perhatikan bahwa fungsi sin(x) memiliki nilai yang terbatas, yaitu antara -1 dan 1, untuk setiap nilai x.

   2. Oleh karena itu, fungsi (sin(x) + 1) juga memiliki nilai yang terbatas, yaitu antara 0 dan 2, untuk setiap nilai x.

   3. Sementara itu, fungsi x akan terus bertambah besar tanpa batas saat x mendekati tak hingga.

   4. Oleh karena itu, nilai dari (sin(x) + 1)/x akan semakin kecil dan mendekati nol saat x mendekati tak hingga.

   Jadi, nilai dari

   lim_x→∞ (sin(x) + 1)/x = 0

Kesulitan dalam Memahami Limit Fungsi Trigonometri Tak Hingga: Contoh Soal Limit Fungsi Trigonometri Tak Hingga

Limit fungsi trigonometri tak hingga adalah konsep yang cukup menantang bagi banyak siswa. Memahami bagaimana fungsi trigonometri berperilaku saat nilai input mendekati tak hingga membutuhkan pemahaman yang kuat tentang konsep limit, fungsi trigonometri, dan sifat-sifatnya. Kesulitan yang dihadapi siswa dalam memahami konsep ini seringkali berasal dari beberapa faktor, seperti kurangnya pemahaman tentang sifat-sifat fungsi trigonometri, kesulitan dalam memvisualisasikan perilaku fungsi saat input mendekati tak hingga, dan kurangnya pengalaman dalam menyelesaikan soal-soal terkait.

Identifikasi Kesulitan Umum, Contoh soal limit fungsi trigonometri tak hingga

Beberapa kesulitan umum yang dihadapi siswa dalam memahami limit fungsi trigonometri tak hingga adalah:

• Kurangnya pemahaman tentang sifat-sifat fungsi trigonometri. Fungsi trigonometri memiliki sifat-sifat unik yang berbeda dari fungsi aljabar. Misalnya, fungsi sinus dan cosinus memiliki periode 2π, yang berarti bahwa nilai fungsi berulang setiap 2π. Pemahaman yang kuat tentang sifat-sifat ini sangat penting untuk memahami perilaku fungsi trigonometri saat input mendekati tak hingga.
• Kesulitan dalam memvisualisasikan perilaku fungsi saat input mendekati tak hingga. Grafik fungsi trigonometri dapat menjadi kompleks, dan sulit untuk memvisualisasikan bagaimana fungsi berperilaku saat input mendekati tak hingga. Hal ini dapat membuat sulit untuk memahami konsep limit.
• Kurangnya pengalaman dalam menyelesaikan soal-soal terkait. Banyak siswa merasa kesulitan dalam menyelesaikan soal-soal limit fungsi trigonometri tak hingga karena kurangnya pengalaman dalam menerapkan konsep dan teknik yang diperlukan.

Tips dan Strategi untuk Mengatasi Kesulitan

Ada beberapa tips dan strategi yang dapat membantu siswa mengatasi kesulitan dalam memahami limit fungsi trigonometri tak hingga:

• Kuasai sifat-sifat fungsi trigonometri. Pastikan siswa memahami sifat-sifat dasar fungsi trigonometri, seperti periode, amplitude, dan nilai maksimum dan minimum. Gunakan grafik dan contoh untuk membantu siswa memvisualisasikan sifat-sifat ini.
• Gunakan grafik untuk memvisualisasikan perilaku fungsi. Gunakan perangkat lunak grafik atau alat online untuk memvisualisasikan perilaku fungsi trigonometri saat input mendekati tak hingga. Hal ini dapat membantu siswa memahami konsep limit secara lebih intuitif.
• Latih dengan soal-soal yang beragam. Selesaikan soal-soal latihan yang beragam untuk membantu siswa menguasai konsep dan teknik yang diperlukan untuk menyelesaikan soal-soal limit fungsi trigonometri tak hingga. Mulai dari soal-soal sederhana dan tingkatkan kesulitan secara bertahap.

Peran Tutor atau Guru

Tutor atau guru memainkan peran penting dalam membantu siswa memahami konsep limit fungsi trigonometri tak hingga. Mereka dapat:

• Menjelaskan konsep dengan jelas dan ringkas. Gunakan bahasa yang mudah dipahami dan berikan contoh yang relevan untuk membantu siswa memahami konsep.
• Membantu siswa mengatasi kesulitan yang dihadapi. Identifikasi kesulitan yang dihadapi siswa dan berikan dukungan dan bimbingan yang tepat.
• Memberikan latihan dan umpan balik. Berikan latihan yang cukup dan berikan umpan balik yang konstruktif untuk membantu siswa menguasai konsep dan teknik yang diperlukan.
• Membuat pembelajaran interaktif. Gunakan metode pembelajaran interaktif, seperti diskusi kelas, presentasi, dan proyek, untuk membuat pembelajaran lebih menarik dan efektif.

Aplikasi dan Perangkat Lunak untuk Membantu Pemahaman Limit Fungsi Trigonometri Tak Hingga

Mempelajari limit fungsi trigonometri tak hingga bisa menjadi tantangan tersendiri bagi sebagian siswa. Untungnya, ada beberapa aplikasi dan perangkat lunak yang dirancang khusus untuk membantu siswa dalam memahami konsep ini dengan lebih mudah. Aplikasi dan perangkat lunak ini dilengkapi dengan fitur-fitur interaktif yang dapat membantu siswa dalam memvisualisasikan dan menganalisis fungsi trigonometri, serta menyelesaikan soal latihan dengan lebih efektif.

Aplikasi dan Perangkat Lunak untuk Membantu Pemahaman Limit Fungsi Trigonometri Tak Hingga

Berikut adalah beberapa aplikasi dan perangkat lunak yang dapat membantu siswa dalam mempelajari dan memahami limit fungsi trigonometri tak hingga:

• GeoGebra: GeoGebra adalah aplikasi matematika gratis dan open-source yang dapat digunakan untuk memvisualisasikan fungsi trigonometri, menggambar grafik, dan menyelesaikan soal latihan. Aplikasi ini menawarkan berbagai fitur interaktif yang dapat membantu siswa dalam memahami konsep limit dengan lebih baik. Misalnya, siswa dapat menggunakan fitur “slider” untuk mengubah nilai variabel dan melihat bagaimana hal itu memengaruhi grafik fungsi. Selain itu, GeoGebra juga dapat digunakan untuk menghitung limit secara numerik dan analitik.
• Wolfram Alpha: Wolfram Alpha adalah mesin pencari komputasional yang dapat digunakan untuk menyelesaikan berbagai macam masalah matematika, termasuk limit fungsi trigonometri tak hingga. Aplikasi ini dapat memberikan solusi langkah demi langkah, serta grafik dan representasi visual yang membantu siswa dalam memahami konsep limit. Misalnya, siswa dapat memasukkan fungsi trigonometri dan nilai variabel yang ingin mereka cari limitnya, dan Wolfram Alpha akan menampilkan solusi lengkap beserta penjelasannya.
• Desmos: Desmos adalah aplikasi kalkulator grafis yang dapat digunakan untuk memvisualisasikan fungsi trigonometri dan menghitung limit secara numerik. Aplikasi ini memiliki antarmuka yang mudah digunakan dan dapat membantu siswa dalam memahami konsep limit melalui visualisasi. Selain itu, Desmos juga dapat digunakan untuk membuat animasi yang menunjukkan bagaimana nilai fungsi berubah seiring dengan perubahan nilai variabel, yang dapat membantu siswa dalam memahami konsep limit secara lebih intuitif.
• Mathway: Mathway adalah aplikasi matematika yang dapat digunakan untuk menyelesaikan berbagai macam soal matematika, termasuk limit fungsi trigonometri tak hingga. Aplikasi ini menawarkan solusi langkah demi langkah yang dapat membantu siswa dalam memahami proses penyelesaian soal. Selain itu, Mathway juga memiliki fitur “tutor” yang dapat memberikan penjelasan tambahan tentang konsep limit.

Contoh Penggunaan Aplikasi dan Perangkat Lunak

Berikut adalah contoh penggunaan aplikasi GeoGebra dalam menyelesaikan soal latihan limit fungsi trigonometri tak hingga:

Misalnya, kita ingin mencari limit dari fungsi f(x) = sin(x)/x ketika x mendekati 0. Kita dapat menggunakan GeoGebra untuk memvisualisasikan grafik fungsi ini dan melihat bagaimana nilai fungsi berubah seiring dengan perubahan nilai x. Dengan menggunakan fitur “slider” di GeoGebra, kita dapat mengubah nilai x dan melihat bagaimana grafik fungsi berubah. Kita akan melihat bahwa ketika x mendekati 0, nilai fungsi f(x) mendekati 1. Hal ini menunjukkan bahwa limit dari fungsi f(x) ketika x mendekati 0 adalah 1.

Pembahasan Soal-Soal Limit Fungsi Trigonometri Tak Hingga

Limit fungsi trigonometri tak hingga merupakan konsep yang menarik dalam kalkulus. Pada dasarnya, kita menyelidiki perilaku fungsi trigonometri ketika variabelnya mendekati tak hingga. Untuk menyelesaikan soal-soal ini, kita perlu memahami sifat-sifat khusus dari fungsi trigonometri dan bagaimana mereka berinteraksi dengan konsep limit.

Contoh Soal Limit Fungsi Trigonometri Tak Hingga

Misalnya, kita ingin menentukan limit dari fungsi berikut ketika x mendekati tak hingga:

lim_{x → ∞} (sin(x) / x)

Untuk menyelesaikan soal ini, kita perlu menggunakan beberapa prinsip dasar:

• Fungsi sin(x) terikat antara -1 dan 1, artinya nilai sin(x) selalu berada di antara -1 dan 1, tidak peduli seberapa besar nilai x.
• Ketika x mendekati tak hingga, nilai x menjadi sangat besar, sehingga nilai (sin(x) / x) mendekati nol.

Berdasarkan prinsip ini, kita dapat menyimpulkan bahwa limit dari fungsi tersebut ketika x mendekati tak hingga adalah nol.

lim_{x → ∞} (sin(x) / x) = 0

Ilustrasi Penyelesaian Soal

Ilustrasi berikut menunjukkan bagaimana fungsi sin(x) / x mendekati nol ketika x mendekati tak hingga:

Gambar menunjukkan bahwa ketika x mendekati tak hingga, nilai fungsi sin(x) / x semakin mendekati garis horizontal y = 0. Ini menunjukkan bahwa limit dari fungsi tersebut ketika x mendekati tak hingga adalah nol.

Contoh Soal Limit Fungsi Trigonometri Tak Hingga Berdasarkan Bentuk Fungsi

Limit fungsi trigonometri tak hingga merupakan konsep penting dalam kalkulus. Konsep ini membahas perilaku fungsi trigonometri ketika variabel bebasnya mendekati nilai tak hingga. Terdapat beberapa bentuk fungsi trigonometri yang umum dijumpai dalam soal limit tak hingga. Berikut ini adalah beberapa contoh soal limit fungsi trigonometri tak hingga berdasarkan bentuk fungsi dan langkah-langkah penyelesaiannya.

Limit Fungsi Sin x/x

Salah satu bentuk fungsi trigonometri yang sering muncul dalam soal limit tak hingga adalah sin x/x. Bentuk ini memiliki sifat unik yang memudahkan kita dalam menentukan limitnya.

• Contoh Soal: Tentukan limit dari lim_x→∞ sin x/x
• Langkah Penyelesaian:
  1. Perhatikan bahwa nilai sin x selalu berada di antara -1 dan 1, yaitu -1 ≤ sin x ≤ 1.
  2. Bagilah kedua ruas pertidaksamaan tersebut dengan x, sehingga diperoleh -1/x ≤ sin x/x ≤ 1/x.
  3. Ambil limit kedua ruas pertidaksamaan ketika x mendekati tak hingga. Karena 1/x mendekati 0 ketika x mendekati tak hingga, maka kita dapatkan lim_x→∞ -1/x = 0 dan lim_x→∞ 1/x = 0.
  4. Berdasarkan teorema apit, jika limit kedua ruas pertidaksamaan sama, maka limit fungsi di tengah juga sama dengan nilai tersebut. Jadi, lim_x→∞ sin x/x = 0.

Limit Fungsi Cos x/x

Bentuk fungsi cos x/x juga sering dijumpai dalam soal limit tak hingga. Penentuan limitnya mirip dengan bentuk sin x/x, namun dengan sedikit perbedaan.

• Contoh Soal: Tentukan limit dari lim_x→∞ cos x/x
• Langkah Penyelesaian:
  1. Perhatikan bahwa nilai cos x selalu berada di antara -1 dan 1, yaitu -1 ≤ cos x ≤ 1.
  2. Bagilah kedua ruas pertidaksamaan tersebut dengan x, sehingga diperoleh -1/x ≤ cos x/x ≤ 1/x.
  3. Ambil limit kedua ruas pertidaksamaan ketika x mendekati tak hingga. Karena 1/x mendekati 0 ketika x mendekati tak hingga, maka kita dapatkan lim_x→∞ -1/x = 0 dan lim_x→∞ 1/x = 0.
  4. Berdasarkan teorema apit, jika limit kedua ruas pertidaksamaan sama, maka limit fungsi di tengah juga sama dengan nilai tersebut. Jadi, lim_x→∞ cos x/x = 0.

Limit Fungsi Tan x/x

Bentuk fungsi tan x/x merupakan kombinasi dari fungsi sin x dan cos x. Untuk menentukan limitnya, kita dapat memanfaatkan identitas trigonometri tan x = sin x/cos x.

• Contoh Soal: Tentukan limit dari lim_x→∞ tan x/x
• Langkah Penyelesaian:
  1. Gunakan identitas trigonometri tan x = sin x/cos x, sehingga diperoleh lim_x→∞ tan x/x = lim_x→∞ (sin x/cos x)/x.
  2. Sederhanakan bentuk tersebut menjadi lim_x→∞ sin x/(x cos x).
  3. Perhatikan bahwa nilai sin x selalu berada di antara -1 dan 1, yaitu -1 ≤ sin x ≤ 1, dan nilai cos x selalu berada di antara -1 dan 1, yaitu -1 ≤ cos x ≤ 1.
  4. Dengan demikian, -1/(x cos x) ≤ sin x/(x cos x) ≤ 1/(x cos x).
  5. Ambil limit kedua ruas pertidaksamaan ketika x mendekati tak hingga. Karena 1/(x cos x) mendekati 0 ketika x mendekati tak hingga, maka kita dapatkan lim_x→∞ -1/(x cos x) = 0 dan lim_x→∞ 1/(x cos x) = 0.
  6. Berdasarkan teorema apit, jika limit kedua ruas pertidaksamaan sama, maka limit fungsi di tengah juga sama dengan nilai tersebut. Jadi, lim_x→∞ tan x/x = 0.

Limit Fungsi Lain

Selain bentuk-bentuk fungsi yang telah disebutkan, masih banyak bentuk fungsi trigonometri lainnya yang mungkin dijumpai dalam soal limit tak hingga. Beberapa contohnya adalah:

• lim_x→∞ sin² x/x
• lim_x→∞ cos² x/x
• lim_x→∞ tan² x/x

Untuk menyelesaikan soal limit fungsi trigonometri tak hingga yang melibatkan bentuk-bentuk fungsi ini, kita dapat memanfaatkan identitas trigonometri dan teorema apit, seperti yang telah dijelaskan sebelumnya.

Tabel Ringkasan Contoh Soal dan Langkah Penyelesaian

Bentuk Fungsi	Contoh Soal	Langkah Penyelesaian
sin x/x	limx→∞ sin x/x	-1 ≤ sin x ≤ 1 -1/x ≤ sin x/x ≤ 1/x limx→∞ -1/x = 0, limx→∞ 1/x = 0 limx→∞ sin x/x = 0
cos x/x	limx→∞ cos x/x	-1 ≤ cos x ≤ 1 -1/x ≤ cos x/x ≤ 1/x limx→∞ -1/x = 0, limx→∞ 1/x = 0 limx→∞ cos x/x = 0
tan x/x	limx→∞ tan x/x	tan x = sin x/cos x limx→∞ sin x/(x cos x) -1/(x cos x) ≤ sin x/(x cos x) ≤ 1/(x cos x) limx→∞ -1/(x cos x) = 0, limx→∞ 1/(x cos x) = 0 limx→∞ tan x/x = 0

Contoh Soal Limit Fungsi Trigonometri Tak Hingga dengan Penerapan Teorema L’Hopital

Limit fungsi trigonometri tak hingga merupakan konsep penting dalam kalkulus yang mempelajari perilaku fungsi trigonometri ketika variabel bebas mendekati nilai tak hingga. Untuk menyelesaikan soal limit fungsi trigonometri tak hingga yang berbentuk tak tentu, kita dapat menggunakan teorema L’Hopital. Teorema ini menyatakan bahwa jika limit suatu fungsi berbentuk tak tentu, maka limit tersebut dapat dihitung dengan cara mengambil turunan dari pembilang dan penyebutnya secara terpisah. Dalam artikel ini, kita akan membahas contoh soal limit fungsi trigonometri tak hingga yang dapat diselesaikan dengan menggunakan teorema L’Hopital, langkah-langkah penyelesaiannya, dan ilustrasi penerapan teorema tersebut.

Contoh Soal

Sebagai contoh, perhatikan soal berikut:

Tentukan nilai limit berikut:

lim_x→∞ (sin(x)/x)

Soal ini merupakan contoh limit fungsi trigonometri tak hingga yang berbentuk tak tentu karena nilai limitnya tidak dapat ditentukan secara langsung. Untuk menyelesaikan soal ini, kita dapat menggunakan teorema L’Hopital.

Langkah-Langkah Penyelesaian

• Pertama, kita perlu memastikan bahwa limit tersebut berbentuk tak tentu. Dalam kasus ini, limitnya berbentuk tak tentu karena sin(x) memiliki nilai antara -1 dan 1, sementara x mendekati tak hingga. Hal ini menghasilkan bentuk tak tentu 0/∞.
• Selanjutnya, kita dapat mengambil turunan dari pembilang dan penyebutnya secara terpisah. Turunan dari sin(x) adalah cos(x), dan turunan dari x adalah 1.
• Kemudian, kita dapat menghitung limit dari hasil turunan tersebut. Limit dari cos(x)/1 ketika x mendekati tak hingga adalah 0.

Ilustrasi Penerapan Teorema L’Hopital

Ilustrasi berikut menunjukkan penerapan teorema L’Hopital dalam menyelesaikan soal limit fungsi trigonometri tak hingga yang telah dibahas sebelumnya.

lim_x→∞ (sin(x)/x) = lim_x→∞ (cos(x)/1) = 0

Dari ilustrasi tersebut, kita dapat melihat bahwa teorema L’Hopital membantu kita untuk menghitung limit fungsi trigonometri tak hingga yang berbentuk tak tentu dengan cara mengambil turunan dari pembilang dan penyebutnya secara terpisah.

Simpulan Akhir

Dengan memahami konsep limit fungsi trigonometri tak hingga, kita dapat membuka pintu menuju pemahaman yang lebih dalam tentang perilaku fungsi trigonometri dan penerapannya dalam berbagai bidang. Mempelajari konsep ini membantu kita untuk melihat dunia matematika dengan perspektif yang lebih luas dan mengaplikasikannya dalam berbagai situasi.