Contoh soal logika proposisi dan jawabannya – Logika proposisi merupakan fondasi penting dalam berbagai bidang, mulai dari ilmu komputer hingga filsafat. Mempelajari logika proposisi membantu kita dalam berpikir secara sistematis dan menguji validitas argumen. Dalam artikel ini, kita akan menjelajahi konsep dasar logika proposisi, mulai dari pengertian hingga aplikasi praktisnya. Siapkan diri Anda untuk memahami cara menggabungkan proposisi dengan operator logika, membangun tabel kebenaran, dan menyelesaikan soal-soal logika proposisi dengan berbagai metode.
Contoh soal logika proposisi dan jawabannya akan menjadi panduan yang menarik untuk mengerti bagaimana logika proposisi bekerja dalam praktik. Kita akan membahas operator-operator logika seperti AND, OR, NOT, IF-THEN, dan IF AND ONLY IF, serta menjelajahi hukum-hukum logika proposisi yang penting. Selain itu, kita juga akan mempelajari bentuk normal konjungtif (CNF) dan bentuk normal disjungtif (DNF) sebagai alat untuk menyederhanakan pernyataan logika.
Pengertian Logika Proposisi
Logika proposisi merupakan cabang dari logika formal yang mempelajari proposisi dan hubungan antar proposisi. Proposisi sendiri adalah pernyataan yang bernilai benar atau salah, tetapi tidak keduanya. Sederhananya, logika proposisi adalah cara berpikir sistematis untuk menganalisis pernyataan dan menguji kebenarannya melalui aturan-aturan tertentu.
Contoh Proposisi
Misalnya, “Matahari terbit di timur” merupakan proposisi karena memiliki nilai kebenaran yang pasti, yaitu benar. Sedangkan “Buah apel rasanya enak” bukanlah proposisi karena nilai kebenarannya subjektif dan bergantung pada persepsi masing-masing orang.
Operator Logika
Operator logika digunakan untuk menghubungkan proposisi dan membentuk proposisi baru. Berikut beberapa jenis operator logika yang umum digunakan dalam logika proposisi:
- Konjungsi (∧): “dan”. Proposisi baru bernilai benar jika kedua proposisi yang dihubungkan bernilai benar. Contoh: “Hari ini hujan dan langit mendung.”
- Disjungsi (∨): “atau”. Proposisi baru bernilai benar jika setidaknya satu dari kedua proposisi yang dihubungkan bernilai benar. Contoh: “Saya akan makan siang di rumah atau di kantor.”
- Implikasi (→): “jika … maka …”. Proposisi baru bernilai salah jika proposisi pertama benar dan proposisi kedua salah. Contoh: “Jika hujan, maka jalanan basah.”
- Biimplikasi (↔): “jika dan hanya jika”. Proposisi baru bernilai benar jika kedua proposisi yang dihubungkan memiliki nilai kebenaran yang sama. Contoh: “Saya akan pergi ke bioskop jika dan hanya jika kamu ikut.”
- Negasi (¬): “bukan”. Proposisi baru bernilai benar jika proposisi yang dinegasikan bernilai salah. Contoh: “Hari ini tidak hujan.”
Konjungsi (AND)
Konjungsi, atau yang lebih dikenal dengan operator AND, merupakan salah satu operator logika dasar yang digunakan untuk menggabungkan dua proposisi atau lebih. Operator AND menghasilkan nilai benar (True) jika dan hanya jika semua proposisi yang digabungkan bernilai benar. Jika salah satu atau lebih proposisi bernilai salah, maka hasil konjungsi akan bernilai salah.
Cara Menggabungkan Dua Proposisi dengan Operator AND
Operator AND dilambangkan dengan simbol ‘^’ atau ‘∧’. Cara menggabungkan dua proposisi dengan operator AND adalah dengan menghubungkan kedua proposisi tersebut dengan simbol AND. Misalnya, jika proposisi pertama adalah “Hari ini hujan” dan proposisi kedua adalah “Saya membawa payung”, maka konjungsi dari kedua proposisi tersebut adalah “Hari ini hujan AND Saya membawa payung”.
Contoh Soal Logika Proposisi dengan Operator AND
Berikut adalah contoh soal logika proposisi dengan operator AND:
“Jika hari ini hujan AND saya membawa payung, maka saya tidak akan basah.”
Untuk menyelesaikan soal ini, kita perlu menentukan nilai kebenaran dari setiap proposisi dan kemudian mengaplikasikan operator AND.
Langkah-langkah penyelesaian:
1. Tentukan nilai kebenaran dari setiap proposisi:
– “Hari ini hujan”: Asumsikan hari ini memang hujan, maka proposisi ini bernilai benar (T).
– “Saya membawa payung”: Asumsikan saya membawa payung, maka proposisi ini bernilai benar (T).
– “Saya tidak akan basah”: Karena hari hujan dan saya membawa payung, maka saya tidak akan basah, sehingga proposisi ini bernilai benar (T).
2. Terapkan operator AND:
– Karena kedua proposisi pertama (“Hari ini hujan” dan “Saya membawa payung”) bernilai benar, maka konjungsi dari kedua proposisi tersebut juga bernilai benar (T).
3. Kesimpulan:
– Karena konjungsi dari kedua proposisi pertama bernilai benar, dan proposisi ketiga (“Saya tidak akan basah”) juga bernilai benar, maka seluruh pernyataan “Jika hari ini hujan AND saya membawa payung, maka saya tidak akan basah” bernilai benar (T).
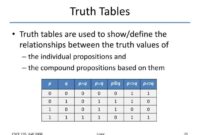
Tabel Kebenaran untuk Operator AND
Tabel kebenaran untuk operator AND dengan 2 variabel proposisi (p dan q) adalah sebagai berikut:
| p | q | p AND q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Dari tabel kebenaran ini, kita dapat melihat bahwa hasil konjungsi (p AND q) hanya bernilai benar jika kedua proposisi (p dan q) bernilai benar. Jika salah satu atau kedua proposisi bernilai salah, maka hasil konjungsi akan bernilai salah.
Disjungsi (OR)
Dalam logika proposisi, disjungsi merupakan salah satu operator logika yang menggabungkan dua proposisi dengan makna “atau”. Operator disjungsi dilambangkan dengan simbol “∨” atau “OR”.
Cara Menggabungkan Dua Proposisi dengan Operator Disjungsi (OR)
Operator disjungsi (OR) menggabungkan dua proposisi, menghasilkan proposisi baru yang bernilai benar jika salah satu atau kedua proposisi awal bernilai benar. Jika kedua proposisi awal bernilai salah, maka proposisi baru yang dihasilkan akan bernilai salah.
Contoh Soal Logika Proposisi dengan Operator OR
Misalnya, kita punya dua proposisi:
* p: Hari ini hujan.
* q: Saya memakai payung.
Jika kita gabungkan kedua proposisi tersebut dengan operator disjungsi (OR), kita akan mendapatkan proposisi baru:
* p ∨ q: Hari ini hujan atau saya memakai payung.
Proposisi baru ini akan bernilai benar jika salah satu atau kedua proposisi awal bernilai benar. Misalnya:
* Jika hari ini hujan (p = benar) dan saya memakai payung (q = benar), maka proposisi baru (p ∨ q) bernilai benar.
* Jika hari ini tidak hujan (p = salah) dan saya memakai payung (q = benar), maka proposisi baru (p ∨ q) bernilai benar.
* Jika hari ini tidak hujan (p = salah) dan saya tidak memakai payung (q = salah), maka proposisi baru (p ∨ q) bernilai salah.
Tabel Kebenaran untuk Operator OR dengan 2 Variabel Proposisi
Tabel kebenaran menunjukkan semua kemungkinan kombinasi nilai kebenaran untuk dua variabel proposisi dan nilai kebenaran dari proposisi yang dihasilkan dengan operator OR.
| p | q | p ∨ q |
|---|---|---|
| Benar | Benar | Benar |
| Benar | Salah | Benar |
| Salah | Benar | Benar |
| Salah | Salah | Salah |
Dari tabel kebenaran, kita dapat melihat bahwa proposisi baru (p ∨ q) bernilai benar dalam tiga dari empat kemungkinan kombinasi nilai kebenaran untuk p dan q, dan hanya bernilai salah ketika kedua proposisi awal (p dan q) bernilai salah.
Negasi (NOT)
Negasi merupakan operator logika yang berfungsi untuk meniadakan nilai kebenaran suatu proposisi. Operator ini dilambangkan dengan simbol “~” atau “¬”.
Cara Meniadakan Suatu Proposisi
Operator negasi digunakan untuk membalikkan nilai kebenaran dari suatu proposisi. Jika suatu proposisi bernilai benar, maka negasinya akan bernilai salah. Sebaliknya, jika suatu proposisi bernilai salah, maka negasinya akan bernilai benar.
Contoh Soal Logika Proposisi dengan Operator NOT
Misalnya, kita punya proposisi “Matahari terbit di barat”. Proposisi ini bernilai salah karena matahari terbit di timur.
Langkah-langkah Penyelesaian:
- Tentukan nilai kebenaran proposisi awal. Dalam contoh ini, proposisi “Matahari terbit di barat” bernilai salah.
- Negasi dari proposisi ini adalah “~(Matahari terbit di barat)”.
- Nilai kebenaran negasi diperoleh dengan membalikkan nilai kebenaran proposisi awal. Karena proposisi awal bernilai salah, maka negasinya bernilai benar.
Tabel Kebenaran untuk Operator NOT
Tabel kebenaran menunjukkan semua kemungkinan kombinasi nilai kebenaran untuk suatu proposisi dan negasinya.
| Proposisi (p) | Negasi (~p) |
|---|---|
| Benar (T) | Salah (F) |
| Salah (F) | Benar (T) |
Tabel ini menunjukkan bahwa ketika proposisi bernilai benar, negasinya bernilai salah, dan sebaliknya.
Implikasi (IF-THEN): Contoh Soal Logika Proposisi Dan Jawabannya

Implikasi adalah salah satu operator logika yang menghubungkan dua proposisi dengan pernyataan “jika … maka …”. Operator ini menyatakan bahwa jika proposisi pertama benar, maka proposisi kedua juga benar. Dalam logika proposisi, operator implikasi sering digunakan untuk merepresentasikan hubungan sebab-akibat atau hubungan syarat-akibat.
Cara Menghubungkan Dua Proposisi dengan Operator Implikasi
Operator implikasi dalam logika proposisi menggunakan simbol “→” untuk menghubungkan dua proposisi. Misalnya, jika “p” menyatakan “hari ini hujan” dan “q” menyatakan “jalan licin”, maka pernyataan “jika hari ini hujan, maka jalan licin” dapat ditulis dalam bentuk logika proposisi sebagai “p → q”.
Contoh Soal Logika Proposisi dengan Operator Implikasi
Berikut adalah contoh soal logika proposisi dengan operator implikasi:
Soal:
“Jika Andi rajin belajar, maka dia akan lulus ujian.”
Penyelesaian:
1. Identifikasi proposisi:
– “Andi rajin belajar” adalah proposisi “p”.
– “Dia akan lulus ujian” adalah proposisi “q”.
2. Tuliskan pernyataan dalam bentuk logika proposisi:
– “Jika Andi rajin belajar, maka dia akan lulus ujian” dapat ditulis sebagai “p → q”.
3. Tentukan nilai kebenaran:
– Jika Andi rajin belajar (p = benar) dan dia lulus ujian (q = benar), maka pernyataan “p → q” adalah benar.
– Jika Andi rajin belajar (p = benar) dan dia tidak lulus ujian (q = salah), maka pernyataan “p → q” adalah salah.
– Jika Andi tidak rajin belajar (p = salah) dan dia lulus ujian (q = benar), maka pernyataan “p → q” adalah benar.
– Jika Andi tidak rajin belajar (p = salah) dan dia tidak lulus ujian (q = salah), maka pernyataan “p → q” adalah benar.
Tabel Kebenaran untuk Operator Implikasi
Tabel kebenaran untuk operator implikasi dengan dua variabel proposisi “p” dan “q” adalah sebagai berikut:
| p | q | p → q |
|---|---|---|
| Benar | Benar | Benar |
| Benar | Salah | Salah |
| Salah | Benar | Benar |
| Salah | Salah | Benar |
Dari tabel kebenaran tersebut, dapat disimpulkan bahwa pernyataan implikasi hanya salah jika proposisi pertama benar dan proposisi kedua salah. Dalam semua kasus lainnya, pernyataan implikasi dianggap benar.
Biimplikasi (IF AND ONLY IF)
Biimplikasi adalah operator logika yang menyatakan bahwa dua proposisi memiliki nilai kebenaran yang sama. Operator ini dilambangkan dengan “↔” atau “iff” (if and only if). Dalam bahasa sehari-hari, biimplikasi dapat diartikan sebagai “jika dan hanya jika”.
Cara Menghubungkan Dua Proposisi dengan Biimplikasi
Operator biimplikasi menghubungkan dua proposisi dengan pernyataan bahwa keduanya benar atau keduanya salah. Proposisi yang dihubungkan dengan operator biimplikasi disebut dengan antecedent dan consequent.
Misalnya, perhatikan proposisi berikut:
- p: Hari ini hujan.
- q: Jalanan basah.
Proposisi p dan q dapat dihubungkan dengan operator biimplikasi seperti ini:
p ↔ q
Ini berarti bahwa “Hari ini hujan jika dan hanya jika jalanan basah”. Pernyataan ini benar jika dan hanya jika kedua proposisi p dan q memiliki nilai kebenaran yang sama.
Contoh Soal Logika Proposisi dengan Operator Biimplikasi
Soal:
Misalkan p: “Mobil berwarna merah” dan q: “Mobil bermesin diesel”. Tuliskan proposisi “Mobil berwarna merah jika dan hanya jika mobil bermesin diesel” dalam bentuk simbol logika.
Penyelesaian:
Proposisi “Mobil berwarna merah jika dan hanya jika mobil bermesin diesel” dapat dituliskan sebagai:
p ↔ q
Langkah-langkah penyelesaian:
1. Identifikasi proposisi: Tentukan proposisi yang terlibat dalam pernyataan. Dalam contoh ini, proposisi p adalah “Mobil berwarna merah” dan proposisi q adalah “Mobil bermesin diesel”.
2. Tentukan operator: Operator yang digunakan dalam pernyataan ini adalah biimplikasi (↔).
3. Hubungkan proposisi dengan operator: Hubungkan proposisi p dan q dengan operator biimplikasi (↔).
Tabel Kebenaran untuk Operator Biimplikasi
Tabel kebenaran untuk operator biimplikasi menunjukkan nilai kebenaran dari proposisi biimplikasi berdasarkan nilai kebenaran dari antecedent dan consequent.
Berikut adalah tabel kebenaran untuk operator biimplikasi dengan dua variabel proposisi:
| p | q | p ↔ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Dari tabel kebenaran, dapat dilihat bahwa:
- Biimplikasi bernilai benar jika dan hanya jika antecedent dan consequent memiliki nilai kebenaran yang sama (keduanya benar atau keduanya salah).
- Biimplikasi bernilai salah jika antecedent dan consequent memiliki nilai kebenaran yang berbeda (salah satu benar dan yang lain salah).
Hukum-hukum Logika Proposisi
Logika proposisi adalah cabang dari logika matematika yang mempelajari pernyataan-pernyataan dan hubungan di antara mereka. Pernyataan dalam logika proposisi adalah kalimat yang memiliki nilai kebenaran, yaitu benar atau salah. Hukum-hukum logika proposisi merupakan aturan yang mengatur bagaimana pernyataan-pernyataan tersebut dapat dihubungkan dan dimanipulasi secara logis. Hukum-hukum ini sangat penting dalam memahami dan menyederhanakan pernyataan-pernyataan logika yang kompleks.
Hukum-hukum Logika Proposisi
Berikut beberapa hukum logika proposisi yang penting dan contoh penerapannya:
- Hukum Identitas: p ≡ p. Artinya, suatu proposisi sama dengan dirinya sendiri. Contoh: “Hari ini adalah hari Selasa” ≡ “Hari ini adalah hari Selasa”.
- Hukum Kontradiksi: ¬(p ∧ ¬p). Artinya, suatu proposisi dan negasinya tidak dapat benar bersamaan. Contoh: “Hari ini hujan” dan “Hari ini tidak hujan” tidak dapat benar bersamaan.
- Hukum Tertium Non Datur: p ∨ ¬p. Artinya, suatu proposisi atau negasinya harus benar. Contoh: “Mobil ini berwarna merah” atau “Mobil ini tidak berwarna merah” harus benar.
- Hukum Komutatif: p ∧ q ≡ q ∧ p dan p ∨ q ≡ q ∨ p. Artinya, urutan proposisi dalam konjungsi atau disjungsi tidak memengaruhi nilai kebenarannya. Contoh: “Hari ini hujan dan langit mendung” ≡ “Langit mendung dan hari ini hujan”.
- Hukum Asosiatif: (p ∧ q) ∧ r ≡ p ∧ (q ∧ r) dan (p ∨ q) ∨ r ≡ p ∨ (q ∨ r). Artinya, cara pengelompokan proposisi dalam konjungsi atau disjungsi tidak memengaruhi nilai kebenarannya. Contoh: “(Hari ini hujan dan langit mendung) dan suhu dingin” ≡ “Hari ini hujan dan (langit mendung dan suhu dingin)”.
- Hukum Distributif: p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) dan p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r). Artinya, konjungsi dapat didistribusikan terhadap disjungsi dan sebaliknya. Contoh: “Hari ini hujan dan (langit mendung atau suhu dingin)” ≡ “(Hari ini hujan dan langit mendung) atau (hari ini hujan dan suhu dingin)”.
- Hukum De Morgan: ¬(p ∧ q) ≡ ¬p ∨ ¬q dan ¬(p ∨ q) ≡ ¬p ∧ ¬q. Artinya, negasi dari konjungsi sama dengan disjungsi dari negasi kedua proposisi, dan negasi dari disjungsi sama dengan konjungsi dari negasi kedua proposisi. Contoh: “Tidak benar bahwa hari ini hujan dan langit mendung” ≡ “Hari ini tidak hujan atau langit tidak mendung”.
- Hukum Implikasi: p → q ≡ ¬p ∨ q. Artinya, implikasi dapat dinyatakan sebagai disjungsi dari negasi dari anteceden dan konsekuen. Contoh: “Jika hari ini hujan, maka jalanan basah” ≡ “Hari ini tidak hujan atau jalanan basah”.
- Hukum Kontraposisi: p → q ≡ ¬q → ¬p. Artinya, implikasi setara dengan kontraposisinya. Contoh: “Jika hari ini hujan, maka jalanan basah” ≡ “Jika jalanan tidak basah, maka hari ini tidak hujan”.
- Hukum Biimplikasi: p ↔ q ≡ (p → q) ∧ (q → p). Artinya, biimplikasi dapat dinyatakan sebagai konjungsi dari implikasi dan inversnya. Contoh: “Hari ini hujan jika dan hanya jika jalanan basah” ≡ “(Jika hari ini hujan, maka jalanan basah) dan (jika jalanan basah, maka hari ini hujan)”.
Contoh Penerapan Hukum Logika Proposisi
Hukum-hukum logika proposisi dapat digunakan untuk menyederhanakan pernyataan logika yang kompleks. Sebagai contoh, perhatikan pernyataan berikut:
“Jika hari ini hujan dan langit mendung, maka jalanan basah.”
Pernyataan ini dapat ditulis dalam bentuk logika proposisi sebagai berikut:
(p ∧ q) → r
di mana:
- p: Hari ini hujan.
- q: Langit mendung.
- r: Jalanan basah.
Dengan menggunakan hukum De Morgan, pernyataan tersebut dapat disederhanakan menjadi:
¬(p ∧ q) ∨ r
Selanjutnya, dengan menggunakan hukum distributif, pernyataan tersebut dapat disederhanakan lagi menjadi:
(¬p ∨ ¬q) ∨ r
Pernyataan yang telah disederhanakan ini lebih mudah dipahami dan dianalisis dibandingkan dengan pernyataan awal.
Tabel Hukum Logika Proposisi
| Hukum | Rumus | Contoh |
|---|---|---|
| Identitas | p ≡ p | “Hari ini adalah hari Selasa” ≡ “Hari ini adalah hari Selasa” |
| Kontradiksi | ¬(p ∧ ¬p) | “Hari ini hujan” dan “Hari ini tidak hujan” tidak dapat benar bersamaan. |
| Tertium Non Datur | p ∨ ¬p | “Mobil ini berwarna merah” atau “Mobil ini tidak berwarna merah” harus benar. |
| Komutatif | p ∧ q ≡ q ∧ p dan p ∨ q ≡ q ∨ p | “Hari ini hujan dan langit mendung” ≡ “Langit mendung dan hari ini hujan”. |
| Asosiatif | (p ∧ q) ∧ r ≡ p ∧ (q ∧ r) dan (p ∨ q) ∨ r ≡ p ∨ (q ∨ r) | “(Hari ini hujan dan langit mendung) dan suhu dingin” ≡ “Hari ini hujan dan (langit mendung dan suhu dingin)”. |
| Distributif | p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r) dan p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) | “Hari ini hujan dan (langit mendung atau suhu dingin)” ≡ “(Hari ini hujan dan langit mendung) atau (hari ini hujan dan suhu dingin)”. |
| De Morgan | ¬(p ∧ q) ≡ ¬p ∨ ¬q dan ¬(p ∨ q) ≡ ¬p ∧ ¬q | “Tidak benar bahwa hari ini hujan dan langit mendung” ≡ “Hari ini tidak hujan atau langit tidak mendung”. |
| Implikasi | p → q ≡ ¬p ∨ q | “Jika hari ini hujan, maka jalanan basah” ≡ “Hari ini tidak hujan atau jalanan basah”. |
| Kontraposisi | p → q ≡ ¬q → ¬p | “Jika hari ini hujan, maka jalanan basah” ≡ “Jika jalanan tidak basah, maka hari ini tidak hujan”. |
| Biimplikasi | p ↔ q ≡ (p → q) ∧ (q → p) | “Hari ini hujan jika dan hanya jika jalanan basah” ≡ “(Jika hari ini hujan, maka jalanan basah) dan (jika jalanan basah, maka hari ini hujan)”. |
Bentuk Normal Konjungtif (CNF)
Bentuk Normal Konjungtif (CNF) adalah representasi standar dalam logika proposisi. CNF memungkinkan kita untuk menuliskan pernyataan logika dalam bentuk yang terstruktur dan mudah diproses, khususnya dalam aplikasi seperti pembuktian otomatis teorema dan desain sirkuit.
Pengertian Bentuk Normal Konjungtif (CNF), Contoh soal logika proposisi dan jawabannya
CNF adalah bentuk standar untuk menyatakan pernyataan logika. Dalam CNF, pernyataan diuraikan menjadi klausa-klausa, di mana setiap klausa adalah disjungsi (OR) dari literal. Literal adalah proposisi atau negasi proposisi. Klausa-klausa ini kemudian dihubungkan dengan konjungsi (AND). Dengan kata lain, CNF adalah konjungsi dari disjungsi literal.
CNF = (literal1 ∨ literal2 ∨ … ∨ literaln) ∧ (literal1 ∨ literal2 ∨ … ∨ literalm) ∧ … ∧ (literal1 ∨ literal2 ∨ … ∨ literalk)
Contoh Pernyataan Logika dalam Bentuk CNF
Misalnya, kita punya pernyataan logika: “Jika hari hujan, maka saya membawa payung atau saya memakai jas hujan.”
Pertama, kita perlu mendefinisikan proposisi:
– p: Hari hujan
– q: Saya membawa payung
– r: Saya memakai jas hujan
Pernyataan tersebut dapat ditulis dalam bentuk implikasi: p → (q ∨ r)
Kemudian, kita dapat mengubah pernyataan tersebut ke dalam CNF dengan menggunakan hukum-hukum logika:
1. Implikasi ke Disjungsi: p → (q ∨ r) ≡ ¬p ∨ (q ∨ r)
2. Asosiatif: ¬p ∨ (q ∨ r) ≡ (¬p ∨ q) ∨ r
3. Distributif: (¬p ∨ q) ∨ r ≡ (¬p ∨ q) ∧ (r ∨ q)
Jadi, bentuk CNF dari pernyataan tersebut adalah: (¬p ∨ q) ∧ (r ∨ q)
Kegunaan Bentuk CNF
Bentuk CNF memiliki beberapa kegunaan penting dalam logika proposisi:
- Pembuktian Otomatis Teorema: CNF memungkinkan kita untuk menggunakan algoritma yang efisien untuk memeriksa apakah suatu pernyataan logika adalah tautologi (benar untuk semua kemungkinan nilai proposisi). Algoritma ini bekerja dengan memeriksa apakah semua klausa dalam CNF dapat dipenuhi secara bersamaan.
- Desain Sirkuit: CNF digunakan dalam desain sirkuit digital untuk merepresentasikan fungsi Boolean. Setiap klausa dalam CNF dapat diimplementasikan sebagai gerbang OR, dan seluruh CNF dapat diimplementasikan sebagai gerbang AND.
- Pemecahan Masalah Logika: CNF dapat digunakan untuk merepresentasikan masalah logika dalam bentuk standar, yang memungkinkan kita untuk menggunakan algoritma pencarian untuk menemukan solusi.
Bentuk Normal Disjungtif (DNF)
Bentuk Normal Disjungtif (DNF) adalah salah satu bentuk standar dalam logika proposisi yang digunakan untuk merepresentasikan pernyataan logika. Dalam bentuk DNF, pernyataan logika ditulis sebagai disjungsi (atau) dari satu atau lebih klausa, di mana setiap klausa adalah konjungsi (dan) dari satu atau lebih literal. Literal adalah variabel proposisi atau negasi dari variabel proposisi.
Pengertian Bentuk Normal Disjungtif (DNF)
Bentuk Normal Disjungtif (DNF) merupakan representasi dari pernyataan logika dalam bentuk disjungsi (atau) dari satu atau lebih klausa, di mana setiap klausa adalah konjungsi (dan) dari satu atau lebih literal.
Literal adalah variabel proposisi atau negasi dari variabel proposisi.
Sebagai contoh, pernyataan logika “p dan (q atau r)” dapat ditulis dalam bentuk DNF sebagai “(p dan q) atau (p dan r)”. Dalam contoh ini, ada dua klausa: “(p dan q)” dan “(p dan r)”. Setiap klausa terdiri dari konjungsi dari dua literal: “p” dan “q” pada klausa pertama, dan “p” dan “r” pada klausa kedua.
Contoh Pernyataan Logika dalam Bentuk DNF
Berikut adalah contoh pernyataan logika dan transformasinya ke dalam bentuk DNF:
Misalnya, pernyataan logika “Jika hujan, maka saya akan membawa payung” dapat ditulis dalam bentuk DNF sebagai:
“Tidak hujan atau saya membawa payung”
Pernyataan ini dapat diubah ke dalam bentuk DNF dengan menggunakan hukum distributif:
“¬h atau p”
di mana:
* “h” adalah variabel proposisi yang menyatakan “hujan”.
* “p” adalah variabel proposisi yang menyatakan “saya membawa payung”.
Kegunaan Bentuk DNF
Bentuk DNF memiliki beberapa kegunaan dalam penyelesaian masalah logika, antara lain:
- Memeriksa kesetaraan logika: Dua pernyataan logika dikatakan ekuivalen secara logika jika dan hanya jika bentuk DNF mereka sama.
- Menentukan kebenaran pernyataan: Bentuk DNF dapat digunakan untuk menentukan kebenaran pernyataan logika dengan mengevaluasi kebenaran setiap klausa. Jika setidaknya satu klausa bernilai benar, maka pernyataan tersebut bernilai benar.
- Membangun sirkuit logika: Bentuk DNF dapat digunakan untuk membangun sirkuit logika yang mengimplementasikan pernyataan logika tertentu.
Metode Penyelesaian Soal Logika Proposisi
Logika proposisi merupakan cabang dari logika formal yang mempelajari proposisi dan hubungan antar proposisi. Proposisi adalah pernyataan yang dapat bernilai benar atau salah. Dalam logika proposisi, kita dapat menggabungkan proposisi-proposisi dengan operator logika untuk membentuk proposisi majemuk. Untuk menyelesaikan soal logika proposisi, kita perlu memahami beberapa metode penyelesaian, seperti tabel kebenaran, deduksi, dan inferensi.
Tabel Kebenaran
Metode tabel kebenaran merupakan metode yang paling umum digunakan untuk menentukan nilai kebenaran dari suatu proposisi majemuk. Metode ini melibatkan pembuatan tabel yang berisi semua kemungkinan kombinasi nilai kebenaran untuk setiap proposisi atom yang terdapat dalam proposisi majemuk. Nilai kebenaran dari proposisi majemuk kemudian ditentukan berdasarkan operator logika yang digunakan.
Berikut adalah contoh soal logika proposisi yang dapat diselesaikan dengan menggunakan metode tabel kebenaran:
Misalkan p adalah proposisi “Hari ini hujan” dan q adalah proposisi “Saya membawa payung”. Tentukan nilai kebenaran dari proposisi majemuk “Jika hari ini hujan, maka saya membawa payung” (p → q).
Untuk menyelesaikan soal ini, kita perlu membuat tabel kebenaran yang berisi semua kemungkinan kombinasi nilai kebenaran untuk p dan q. Berikut adalah tabel kebenarannya:
| p | q | p → q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Dari tabel kebenaran di atas, kita dapat melihat bahwa nilai kebenaran dari proposisi majemuk “Jika hari ini hujan, maka saya membawa payung” (p → q) adalah benar (T) ketika p bernilai benar (T) dan q bernilai benar (T), atau ketika p bernilai salah (F) dan q bernilai benar (T), atau ketika p bernilai salah (F) dan q bernilai salah (F).
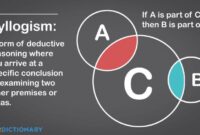
Metode Deduksi
Metode deduksi merupakan metode yang digunakan untuk membuktikan kebenaran suatu proposisi majemuk dengan menggunakan aturan-aturan inferensi. Aturan-aturan inferensi ini merupakan pernyataan logika yang diterima sebagai benar. Dengan menggunakan aturan-aturan inferensi, kita dapat menyimpulkan proposisi majemuk baru dari proposisi-proposisi yang sudah diketahui kebenarannya.
Contoh soal logika proposisi dan jawabannya memang menarik untuk dipelajari. Konsepnya sederhana, tapi bisa jadi rumit saat diterapkan dalam soal-soal yang kompleks. Nah, buat kamu yang sedang belajar tentang bentuk geometri, mungkin kamu juga tertarik dengan contoh soal jajar genjang dan jawabannya.
Contoh soal jajar genjang dan jawabannya ini bisa membantumu memahami konsep jajar genjang dengan lebih baik. Kembali ke soal logika proposisi, memahami konsepnya akan memudahkan kamu dalam memecahkan berbagai masalah logika, baik dalam kehidupan sehari-hari maupun dalam bidang akademis.
Berikut adalah contoh soal logika proposisi yang dapat diselesaikan dengan menggunakan metode deduksi:
Misalkan p adalah proposisi “Semua mahasiswa adalah manusia” dan q adalah proposisi “Semua manusia adalah makhluk hidup”. Buktikan bahwa proposisi “Semua mahasiswa adalah makhluk hidup” (p → r) adalah benar.
Untuk membuktikan proposisi ini, kita dapat menggunakan aturan inferensi modus ponens. Aturan modus ponens menyatakan bahwa jika p adalah benar dan p → q adalah benar, maka q juga benar. Dalam contoh ini, p adalah proposisi “Semua mahasiswa adalah manusia” yang diasumsikan benar, dan p → q adalah proposisi “Jika semua mahasiswa adalah manusia, maka semua mahasiswa adalah makhluk hidup” yang juga diasumsikan benar. Dengan menggunakan aturan modus ponens, kita dapat menyimpulkan bahwa q, yaitu proposisi “Semua mahasiswa adalah makhluk hidup”, juga benar.
Aplikasi Logika Proposisi
Logika proposisi merupakan alat yang sangat berguna dalam berbagai bidang, tidak hanya dalam matematika dan filsafat, tetapi juga dalam ilmu komputer dan teknologi. Logika proposisi memungkinkan kita untuk menganalisis dan memanipulasi pernyataan-pernyataan kompleks dan membuat kesimpulan yang logis.
Penerapan dalam Pemrograman Komputer
Logika proposisi merupakan dasar dari pemrograman komputer. Logika proposisi digunakan untuk mengimplementasikan operator logika dalam bahasa pemrograman, seperti AND, OR, NOT, XOR, dan lainnya. Operator-operator ini digunakan untuk mengontrol alur program, mengevaluasi kondisi, dan membuat keputusan berdasarkan data yang tersedia.
Sebagai contoh, perhatikan kode program berikut:
“`python
if (suhu > 30) and (kelembaban > 80):
print(“Cuaca panas dan lembap”)
elif (suhu > 30) and (kelembaban < 80):
print("Cuaca panas dan kering")
else:
print("Cuaca normal")
“`
Kode ini menggunakan operator logika “and” dan “or” untuk mengevaluasi kondisi cuaca. Program akan mencetak pesan yang sesuai berdasarkan kombinasi suhu dan kelembaban yang terdeteksi. Logika proposisi memastikan bahwa program berjalan sesuai dengan aturan logika yang benar dan menghasilkan output yang akurat.
Penerapan dalam Sistem Pakar
Sistem pakar adalah sistem komputer yang dirancang untuk meniru kemampuan seorang ahli dalam bidang tertentu. Sistem pakar menggunakan logika proposisi untuk merepresentasikan pengetahuan dan aturan pakar dalam bentuk basis pengetahuan. Basis pengetahuan ini kemudian digunakan untuk memecahkan masalah dan memberikan rekomendasi.
Contohnya, dalam sistem pakar medis, aturan pakar dapat direpresentasikan sebagai berikut:
Jika pasien mengalami demam tinggi dan batuk, maka pasien mungkin menderita flu.
Aturan ini dapat direpresentasikan dalam logika proposisi sebagai:
(Demam Tinggi) AND (Batuk) ⇒ (Flu)
Sistem pakar akan menggunakan aturan ini dan data pasien untuk menentukan apakah pasien menderita flu atau tidak.
Penerapan dalam Logika Fuzzy
Logika fuzzy adalah perluasan dari logika proposisi yang memungkinkan untuk menangani informasi yang tidak pasti atau ambigu. Logika fuzzy menggunakan konsep derajat kebenaran, di mana proposisi dapat memiliki nilai kebenaran antara 0 dan 1.
Contohnya, perhatikan pernyataan “Mobil itu cepat”. Dalam logika klasik, pernyataan ini hanya bisa bernilai benar atau salah. Namun, dalam logika fuzzy, pernyataan ini dapat memiliki nilai kebenaran yang berbeda tergantung pada kecepatan mobil. Misalnya, jika mobil melaju dengan kecepatan 100 km/jam, maka nilai kebenaran pernyataan “Mobil itu cepat” mungkin 0,8.
Logika fuzzy memiliki banyak aplikasi dalam berbagai bidang, seperti kontrol sistem, pengambilan keputusan, dan pemrosesan citra.
Akhir Kata
Setelah mempelajari contoh soal logika proposisi dan jawabannya, diharapkan Anda memiliki pemahaman yang lebih baik tentang konsep logika proposisi. Logika proposisi memiliki aplikasi luas dalam berbagai bidang, termasuk pemrograman komputer, sistem pakar, dan logika fuzzy. Kemampuan untuk berpikir logis dan menganalisis argumen dengan tepat merupakan aset berharga dalam berbagai aspek kehidupan.