Contoh Soal Logaritma: Penjumlahan dan Pengurangan

Logaritma, sebuah konsep matematika yang mungkin terdengar rumit, sebenarnya memiliki aplikasi yang luas dalam berbagai bidang, mulai dari sains hingga teknologi. Dalam artikel ini, kita akan menjelajahi contoh soal logaritma penjumlahan dan pengurangan, yang merupakan bagian penting dalam memahami operasi logaritma.

Dengan mempelajari contoh-contoh soal, kita akan memahami bagaimana sifat-sifat logaritma dapat digunakan untuk menyederhanakan operasi logaritma dan memecahkan masalah yang lebih kompleks. Mari kita mulai dengan membahas konsep dasar logaritma dan sifat-sifatnya sebelum kita masuk ke contoh soal penjumlahan dan pengurangan logaritma.

Pengertian Logaritma

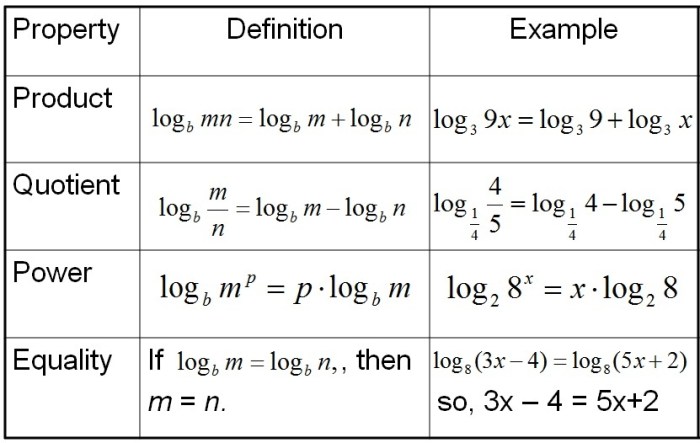
Logaritma adalah konsep matematika yang erat kaitannya dengan eksponen. Secara sederhana, logaritma menjawab pertanyaan: “Pangkat berapa yang harus diberikan pada suatu bilangan dasar untuk mendapatkan suatu bilangan tertentu?”.

Kaitan Logaritma dengan Eksponen

Logaritma dan eksponen merupakan konsep yang saling berhubungan. Jika kita memiliki persamaan eksponen:

a^b = c

Maka, logaritma dari c dengan basis a adalah b. Persamaan logaritma yang sesuai dengan persamaan eksponen di atas adalah:

log_a c = b

Dalam persamaan logaritma, a disebut basis, c disebut numerus, dan b disebut logaritma.

Contoh Logaritma dalam Kehidupan Sehari-hari

Logaritma sering digunakan dalam berbagai bidang, seperti:

• Skala Richter untuk Gempa Bumi: Skala Richter menggunakan logaritma untuk mengukur kekuatan gempa bumi. Setiap peningkatan satu skala Richter menunjukkan peningkatan sepuluh kali lipat dalam amplitudo gelombang seismik. Misalnya, gempa bumi berkekuatan 7 skala Richter sepuluh kali lebih kuat daripada gempa bumi berkekuatan 6 skala Richter.
• Tingkat Keasaman (pH): pH suatu larutan diukur menggunakan logaritma konsentrasi ion hidrogen. Setiap penurunan satu unit pH menunjukkan peningkatan sepuluh kali lipat dalam keasaman.
• Pertumbuhan Populasi: Logaritma dapat digunakan untuk memodelkan pertumbuhan populasi yang eksponensial.

Perbandingan Sifat-sifat Logaritma dan Eksponen

Berikut adalah tabel yang membandingkan sifat-sifat logaritma dan eksponen:

Sifat	Eksponen	Logaritma
Perkalian	am * an = am+n	loga (m * n) = loga m + loga n
Pembagian	am / an = am-n	loga (m / n) = loga m – loga n
Pangkat	(am)n = am*n	loga mn = n * loga m
Basis Sama	a1 = a	loga a = 1
Basis 1	1n = 1	log1 a = tidak terdefinisi

Sifat-sifat Logaritma

Logaritma merupakan fungsi invers dari eksponen. Sifat-sifat logaritma sangat berguna dalam menyelesaikan persamaan logaritma, menyederhanakan operasi logaritma, dan menyelesaikan masalah matematika yang kompleks.

Sifat-sifat Logaritma

Berikut adalah 5 sifat logaritma yang paling penting beserta contoh penerapannya:

• Sifat 1: Logaritma dari hasil kali

  Logaritma dari hasil kali dua bilangan sama dengan jumlah logaritma masing-masing bilangan tersebut.

  log_a (x * y) = log_a x + log_a y

  Contoh: log₂ (8 * 16) = log₂ 8 + log₂ 16 = 3 + 4 = 7

• Sifat 2: Logaritma dari hasil bagi

  Logaritma dari hasil bagi dua bilangan sama dengan selisih logaritma pembilang dan penyebutnya.

  log_a (x / y) = log_a x – log_a y

  Contoh: log₃ (27 / 9) = log₃ 27 – log₃ 9 = 3 – 2 = 1

• Sifat 3: Logaritma dari pangkat

  Logaritma dari suatu bilangan yang dipangkatkan dengan suatu bilangan sama dengan hasil kali pangkat tersebut dengan logaritma bilangan pokoknya.

  log_a (xⁿ) = n * log_a x

  Contoh: log₅ (25²) = 2 * log₅ 25 = 2 * 2 = 4

• Sifat 4: Logaritma dengan basis yang sama

  Jika basis logaritma sama dengan bilangan yang dicari logaritmanya, maka nilai logaritma tersebut adalah 1.

  log_a a = 1

  Contoh: log₇ 7 = 1

• Sifat 5: Logaritma dari 1

  Logaritma dari 1 dengan basis a selalu sama dengan 0.

  log_a 1 = 0

  Contoh: log₃ 1 = 0

Penggunaan Sifat-sifat Logaritma untuk Menyederhanakan Operasi Logaritma

Sifat-sifat logaritma dapat digunakan untuk menyederhanakan operasi logaritma yang kompleks. Contohnya, persamaan logaritma log₂ (8x) + log₂ (x/2) dapat disederhanakan dengan menggunakan sifat 1 dan 2:

log₂ (8x) + log₂ (x/2) = log₂ (8x * x/2) = log₂ (4x²)

Persamaan ini kemudian dapat diselesaikan dengan menggunakan sifat-sifat logaritma lainnya.

Tabel Sifat-sifat Logaritma

Sifat	Rumus	Contoh
Logaritma dari hasil kali	loga (x * y) = loga x + loga y	log2 (8 * 16) = log2 8 + log2 16 = 3 + 4 = 7
Logaritma dari hasil bagi	loga (x / y) = loga x – loga y	log3 (27 / 9) = log3 27 – log3 9 = 3 – 2 = 1
Logaritma dari pangkat	loga (xn) = n * loga x	log5 (252) = 2 * log5 25 = 2 * 2 = 4
Logaritma dengan basis yang sama	loga a = 1	log7 7 = 1
Logaritma dari 1	loga 1 = 0	log3 1 = 0

Penjumlahan dan Pengurangan Logaritma

Logaritma merupakan fungsi invers dari eksponen. Dalam mempelajari logaritma, kita akan menemukan operasi penjumlahan dan pengurangan logaritma. Penjumlahan dan pengurangan logaritma dengan basis yang sama memiliki aturan khusus yang perlu dipahami.

Konsep Penjumlahan dan Pengurangan Logaritma

Penjumlahan dan pengurangan logaritma dengan basis yang sama memiliki aturan khusus yang memudahkan kita dalam menyelesaikan operasi tersebut. Berikut penjelasannya:

Penjumlahan Logaritma:

log_a x + log_a y = log_a (x * y)

Aturan ini menyatakan bahwa penjumlahan logaritma dengan basis yang sama dari dua bilangan sama dengan logaritma dari hasil kali kedua bilangan tersebut.

Pengurangan Logaritma:

log_a x – log_a y = log_a (x / y)

Aturan ini menyatakan bahwa pengurangan logaritma dengan basis yang sama dari dua bilangan sama dengan logaritma dari hasil bagi kedua bilangan tersebut.

Contoh Soal Penjumlahan dan Pengurangan Logaritma

Berikut contoh soal penjumlahan dan pengurangan logaritma dengan langkah-langkah penyelesaiannya:

1. Tentukan nilai dari log₂ 8 + log₂ 4.

   Penyelesaian:

   log₂ 8 + log₂ 4 = log₂ (8 * 4) = log₂ 32 = 5

   Karena 2⁵ = 32, maka log₂ 32 = 5.

2. Tentukan nilai dari log₃ 27 – log₃ 9.

   Penyelesaian:

   log₃ 27 – log₃ 9 = log₃ (27 / 9) = log₃ 3 = 1

   Karena 3¹ = 3, maka log₃ 3 = 1.

   Contoh soal logaritma penjumlahan dan pengurangan biasanya melibatkan operasi dasar seperti mencari nilai logaritma dari penjumlahan atau pengurangan dua bilangan. Konsep ini mirip dengan rumus vlookup dan hlookup dalam excel, yang berguna untuk mencari data spesifik dalam tabel. Contoh soal rumus vlookup dan hlookup dapat membantu kita memahami bagaimana rumus tersebut bekerja dalam mencari data di tabel.

   Kembali ke logaritma, memahami konsep penjumlahan dan pengurangan pada logaritma sangat penting dalam menyelesaikan soal-soal yang lebih kompleks.

Contoh Soal Logaritma Penjumlahan dan Pengurangan

Logaritma penjumlahan dan pengurangan merupakan salah satu konsep penting dalam matematika, khususnya dalam aljabar. Konsep ini sering digunakan dalam berbagai bidang seperti ilmu komputer, fisika, dan kimia. Untuk memahami lebih dalam tentang logaritma penjumlahan dan pengurangan, mari kita bahas beberapa contoh soal berikut.

Contoh Soal 1: Logaritma Penjumlahan dengan Basis Sama

Contoh soal pertama ini akan membahas tentang logaritma penjumlahan dengan basis yang sama. Soal ini dirancang untuk membantu memahami bagaimana sifat logaritma penjumlahan dapat diterapkan dalam menyelesaikan masalah.

• Tentukan nilai dari log₂ 8 + log₂ 16.

Berikut langkah-langkah penyelesaiannya:

1. Gunakan sifat logaritma penjumlahan: log_a b + log_a c = log_a (b × c).
2. Terapkan sifat tersebut pada soal: log₂ 8 + log₂ 16 = log₂ (8 × 16).
3. Hitung hasil perkalian: log₂ (8 × 16) = log₂ 128.
4. Tentukan nilai logaritma: log₂ 128 = 7, karena 2⁷ = 128.

Jadi, nilai dari log₂ 8 + log₂ 16 adalah 7.

Contoh Soal 2: Logaritma Pengurangan dengan Basis Sama

Contoh soal kedua ini akan membahas tentang logaritma pengurangan dengan basis yang sama. Soal ini dirancang untuk membantu memahami bagaimana sifat logaritma pengurangan dapat diterapkan dalam menyelesaikan masalah.

• Tentukan nilai dari log₃ 81 – log₃ 9.

Berikut langkah-langkah penyelesaiannya:

1. Gunakan sifat logaritma pengurangan: log_a b – log_a c = log_a (b / c).
2. Terapkan sifat tersebut pada soal: log₃ 81 – log₃ 9 = log₃ (81 / 9).
3. Hitung hasil pembagian: log₃ (81 / 9) = log₃ 9.
4. Tentukan nilai logaritma: log₃ 9 = 2, karena 3² = 9.

Jadi, nilai dari log₃ 81 – log₃ 9 adalah 2.

Contoh Soal 3: Logaritma Penjumlahan dan Pengurangan dengan Basis Berbeda

Contoh soal ketiga ini akan membahas tentang logaritma penjumlahan dan pengurangan dengan basis yang berbeda. Soal ini dirancang untuk membantu memahami bagaimana sifat logaritma dapat diterapkan dalam menyelesaikan masalah yang lebih kompleks.

• Tentukan nilai dari log₂ 16 + log₃ 27 – log₅ 125.

Berikut langkah-langkah penyelesaiannya:

1. Hitung nilai masing-masing logaritma:
   • log₂ 16 = 4, karena 2⁴ = 16.
   • log₃ 27 = 3, karena 3³ = 27.
   • log₅ 125 = 3, karena 5³ = 125.
2. Substitusikan nilai logaritma ke dalam soal: 4 + 3 – 3.
3. Hitung hasil penjumlahan dan pengurangan: 4 + 3 – 3 = 4.

Jadi, nilai dari log₂ 16 + log₃ 27 – log₅ 125 adalah 4.

Penerapan Logaritma dalam Kehidupan Sehari-hari

Logaritma, meskipun mungkin tampak seperti konsep matematika yang rumit, sebenarnya memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Dari bidang sains hingga teknologi dan ekonomi, logaritma berperan penting dalam memecahkan masalah kompleks dan memahami pola yang rumit.

Skala Richter dalam Seismologi

Logaritma digunakan dalam seismologi untuk mengukur kekuatan gempa bumi menggunakan skala Richter. Skala ini dirancang untuk mewakili intensitas gempa bumi secara logaritmis, yang berarti setiap peningkatan satu satuan pada skala Richter menunjukkan peningkatan sepuluh kali lipat dalam amplitudo gelombang seismik.

• Sebagai contoh, gempa bumi berkekuatan 6 pada skala Richter sepuluh kali lebih kuat daripada gempa bumi berkekuatan 5.
• Skala logaritmis memungkinkan para ilmuwan untuk mengukur dan membandingkan gempa bumi dengan rentang kekuatan yang sangat luas, dari getaran kecil hingga gempa bumi yang menghancurkan.

Pengukuran Derajat Keasaman (pH)

Logaritma juga digunakan untuk mengukur derajat keasaman (pH) suatu larutan. Skala pH adalah skala logaritmis yang menunjukkan konsentrasi ion hidrogen dalam suatu larutan.

• Skala pH berkisar dari 0 hingga 14, dengan pH 7 menunjukkan larutan netral, pH kurang dari 7 menunjukkan larutan asam, dan pH lebih dari 7 menunjukkan larutan basa.
• Setiap perubahan satu satuan pada skala pH mewakili perubahan sepuluh kali lipat dalam konsentrasi ion hidrogen.

Pertumbuhan Ekonomi dan Investasi

Dalam ekonomi, logaritma digunakan untuk menganalisis pertumbuhan ekonomi dan investasi. Pertumbuhan ekonomi sering kali dinyatakan sebagai persentase, dan logaritma membantu dalam memahami dan memproyeksikan pertumbuhan ini secara akurat.

• Logaritma juga digunakan dalam menghitung nilai waktu uang, yaitu konsep yang menunjukkan bahwa uang yang diterima hari ini bernilai lebih tinggi daripada uang yang diterima di masa depan karena potensi pertumbuhannya.
• Rumus bunga majemuk, yang melibatkan logaritma, digunakan untuk menghitung nilai investasi di masa depan berdasarkan tingkat bunga dan periode investasi.

Soal Latihan Logaritma Penjumlahan dan Pengurangan

Logaritma penjumlahan dan pengurangan merupakan operasi dasar dalam matematika yang penting untuk dipahami. Soal-soal latihan berikut ini akan membantu kamu dalam mengasah kemampuanmu dalam menyelesaikan operasi logaritma.

Soal Latihan

Berikut adalah lima soal latihan logaritma penjumlahan dan pengurangan dengan tingkat kesulitan yang bervariasi.

1. Tentukan nilai dari log₂ 8 + log₂ 16.
2. Hitunglah hasil dari log₃ 27 – log₃ 9.
3. Sederhanakan persamaan logaritma berikut: log₅ 25 + log₅ 125 – log₅ 5.
4. Tentukan nilai x yang memenuhi persamaan logaritma: log₄ (x + 3) + log₄ (x – 1) = 1.
5. Selesaikan persamaan logaritma berikut: log₂ (x² – 4) – log₂ (x + 2) = 2.

Kunci Jawaban

1. log₂ 8 + log₂ 16 = 3 + 4 = 7
2. log₃ 27 – log₃ 9 = 3 – 2 = 1
3. log₅ 25 + log₅ 125 – log₅ 5 = 2 + 3 – 1 = 4
4. log₄ (x + 3) + log₄ (x – 1) = 1
   
   log₄ [(x + 3)(x – 1)] = 1
   
   (x + 3)(x – 1) = 4
   
   x² + 2x – 7 = 0
   
   x = (-2 ± √32) / 2
   
   x = -1 ± 2√2
   
   Jadi, nilai x yang memenuhi persamaan adalah x = -1 + 2√2 atau x = -1 – 2√2.
5. log₂ (x² – 4) – log₂ (x + 2) = 2
   
   log₂ [(x² – 4) / (x + 2)] = 2
   
   (x² – 4) / (x + 2) = 2²
   
   x² – 4 = 4(x + 2)
   
   x² – 4x – 12 = 0
   
   (x – 6)(x + 2) = 0
   
   x = 6 atau x = -2
   
   Karena x = -2 tidak memenuhi syarat (membuat penyebut nol), maka nilai x yang memenuhi persamaan adalah x = 6.

Petunjuk Tambahan

Berikut adalah beberapa petunjuk tambahan yang dapat membantu kamu dalam menyelesaikan soal latihan logaritma penjumlahan dan pengurangan:

• Ingat sifat logaritma: log_a b + log_a c = log_a (b * c) dan log_a b – log_a c = log_a (b / c).
• Gunakan sifat logaritma untuk menyederhanakan persamaan sebelum menyelesaikannya.
• Jika kamu kesulitan dalam menyelesaikan soal latihan, cobalah untuk mencari bantuan dari guru atau teman sekelasmu.

Strategi Menyelesaikan Soal Logaritma Penjumlahan dan Pengurangan

Logaritma merupakan konsep matematika yang penting dan sering muncul dalam berbagai bidang, seperti fisika, kimia, dan ekonomi. Soal logaritma penjumlahan dan pengurangan seringkali menjadi tantangan bagi siswa, karena membutuhkan pemahaman yang mendalam tentang sifat-sifat logaritma dan kemampuan untuk memanipulasi persamaan logaritma dengan tepat. Untuk membantu Anda mengatasi tantangan ini, berikut beberapa strategi efektif yang dapat Anda gunakan dalam menyelesaikan soal logaritma penjumlahan dan pengurangan.

Identifikasi Pola dan Sifat Logaritma

Langkah pertama dalam menyelesaikan soal logaritma adalah mengidentifikasi pola dan sifat logaritma yang relevan dengan soal tersebut. Salah satu sifat logaritma yang paling penting adalah sifat logaritma penjumlahan dan pengurangan. Sifat ini menyatakan bahwa logaritma dari hasil kali dua bilangan sama dengan jumlah logaritma kedua bilangan tersebut, dan logaritma dari hasil bagi dua bilangan sama dengan selisih logaritma kedua bilangan tersebut.

• Sifat Logaritma Penjumlahan:

  log_a (x * y) = log_a x + log_a y

• Sifat Logaritma Pengurangan:

  log_a (x / y) = log_a x – log_a y

Langkah-Langkah Penting dalam Menyelesaikan Soal Logaritma

Langkah	Penjelasan
1. Identifikasi Pola dan Sifat Logaritma	Tentukan sifat logaritma yang relevan dengan soal yang diberikan.
2. Sederhanakan Persamaan	Gunakan sifat logaritma untuk menyederhanakan persamaan logaritma.
3. Gunakan Operasi Aljabar	Terapkan operasi aljabar untuk menyelesaikan persamaan logaritma.
4. Periksa Jawaban	Pastikan jawaban yang diperoleh memenuhi persamaan logaritma asli.

Kesalahan Umum dalam Menyelesaikan Soal Logaritma: Contoh Soal Logaritma Penjumlahan Dan Pengurangan

Logaritma adalah konsep matematika yang penting dan sering muncul dalam berbagai bidang, mulai dari ilmu komputer hingga keuangan. Namun, menyelesaikan soal logaritma bisa menjadi tantangan bagi sebagian siswa. Ada beberapa kesalahan umum yang sering dilakukan, yang dapat menyebabkan jawaban yang salah atau tidak lengkap.

Kesalahan 1: Tidak Memahami Sifat-sifat Logaritma

Salah satu kesalahan umum adalah tidak memahami sifat-sifat logaritma dengan baik. Misalnya, banyak siswa lupa bahwa logaritma merupakan operasi invers dari eksponen. Mereka juga mungkin tidak familier dengan sifat-sifat penting seperti:

• log_a 1 = 0
• log_a a = 1
• log_a (b * c) = log_a b + log_a c
• log_a (b / c) = log_a b – log_a c
• log_a bⁿ = n * log_a b

Memahami sifat-sifat ini sangat penting untuk menyelesaikan soal logaritma dengan benar.

Kesalahan 2: Mencampuradukkan Operasi Logaritma dengan Operasi Aritmetika

Kesalahan lain yang sering terjadi adalah mencampuradukkan operasi logaritma dengan operasi aritmetika. Misalnya, siswa mungkin mencoba menjumlahkan atau mengurangkan logaritma tanpa memperhatikan basis logaritma.

Perlu diingat bahwa operasi logaritma hanya dapat dilakukan pada logaritma dengan basis yang sama. Jika basisnya berbeda, maka logaritma tersebut harus diubah ke basis yang sama terlebih dahulu.

Kesalahan 3: Tidak Memeriksa Domain Logaritma

Logaritma hanya terdefinisi untuk bilangan positif. Kesalahan umum lainnya adalah tidak memeriksa domain logaritma sebelum melakukan operasi logaritma.

Sebagai contoh, jika kita diminta untuk menyelesaikan persamaan log₂ (x – 1) = 3, kita harus memastikan bahwa x – 1 > 0. Jika tidak, maka logaritma tersebut tidak terdefinisi.

Tips dan Trik untuk Menghindari Kesalahan Umum dalam Logaritma

• Kuasai sifat-sifat logaritma dan aplikasikannya secara tepat dalam menyelesaikan soal.
• Selalu perhatikan basis logaritma dan pastikan bahwa operasi logaritma dilakukan dengan basis yang sama.
• Periksa domain logaritma sebelum melakukan operasi logaritma.
• Latih soal logaritma secara rutin untuk meningkatkan pemahaman dan kemampuan menyelesaikan soal.
• Jangan ragu untuk berkonsultasi dengan guru atau teman sekelas jika mengalami kesulitan dalam memahami konsep logaritma.

Aplikasi Logaritma dalam Teknologi

Logaritma, sebuah konsep matematika yang mungkin tampak rumit, ternyata memiliki aplikasi yang luas dan penting dalam dunia teknologi modern. Logaritma memungkinkan kita untuk menyelesaikan masalah kompleks dengan cara yang efisien, dan berperan penting dalam berbagai bidang, mulai dari komputasi hingga ilmu data.

Algoritma Pencarian

Logaritma berperan penting dalam algoritma pencarian yang efisien, seperti pencarian biner. Dalam algoritma pencarian biner, kita membagi kumpulan data yang diurutkan menjadi dua bagian secara berulang, dan membandingkan elemen yang dicari dengan elemen tengah. Jika elemen yang dicari lebih besar dari elemen tengah, kita mencari di bagian kanan, dan jika lebih kecil, kita mencari di bagian kiri. Proses ini berlanjut hingga elemen yang dicari ditemukan. Karena algoritma pencarian biner membagi data menjadi dua bagian secara berulang, kompleksitas waktu pencariannya adalah logaritmik, yaitu O(log n), di mana n adalah jumlah elemen dalam kumpulan data. Hal ini berarti bahwa semakin besar kumpulan data, semakin sedikit langkah yang diperlukan untuk menemukan elemen yang dicari.

Kompresi Data

Logaritma juga digunakan dalam kompresi data, yang merupakan proses mengurangi ukuran file tanpa kehilangan informasi penting. Metode kompresi data seperti Huffman coding dan Lempel-Ziv menggunakan logaritma untuk menentukan kode yang paling efisien untuk mewakili data. Dengan menggunakan logaritma, metode kompresi data dapat mencapai tingkat kompresi yang tinggi, yang memungkinkan penyimpanan dan transmisi data yang lebih efisien.

Contoh Aplikasi Teknologi, Contoh soal logaritma penjumlahan dan pengurangan

Berikut adalah beberapa contoh aplikasi teknologi yang memanfaatkan konsep logaritma:

• Sistem Navigasi GPS: Sistem navigasi GPS menggunakan logaritma untuk menghitung jarak antara dua titik pada permukaan bumi. Dengan menggunakan logaritma, sistem GPS dapat menentukan posisi pengguna dengan akurasi yang tinggi.
• Algoritma Pembelajaran Mesin: Algoritma pembelajaran mesin seperti regresi logistik dan pohon keputusan menggunakan logaritma untuk memprediksi probabilitas hasil tertentu.
• Spektrum Audio: Dalam audio, logaritma digunakan untuk mengukur dan menampilkan spektrum audio. Karena pendengaran manusia bersifat logaritmik, logaritma digunakan untuk membuat skala frekuensi audio secara linier, sehingga lebih mudah dipahami oleh manusia.

Ilustrasi Penggunaan Logaritma dalam Kompresi Data

Bayangkan sebuah gambar digital yang memiliki banyak warna berbeda. Kompresi data dapat digunakan untuk mengurangi ukuran file gambar dengan mengganti warna yang serupa dengan kode yang lebih pendek. Misalnya, warna merah tua, merah muda, dan merah terang dapat digantikan dengan kode yang sama. Logaritma digunakan untuk menentukan kode yang paling efisien untuk mewakili warna-warna tersebut.

Dengan menggunakan logaritma, kita dapat menemukan kode yang paling efisien untuk mewakili warna-warna yang paling sering muncul dalam gambar, sehingga menghasilkan file gambar yang lebih kecil tanpa kehilangan informasi penting.

Hubungan Logaritma dengan Fungsi Eksponensial

Logaritma dan fungsi eksponensial memiliki hubungan yang erat dan timbal balik. Keduanya saling melengkapi dan dapat digunakan untuk menyelesaikan masalah yang melibatkan pertumbuhan eksponensial, peluruhan, dan lainnya.

Pengertian Fungsi Eksponensial dan Logaritma

Fungsi eksponensial adalah fungsi yang melibatkan pangkat atau eksponen. Bentuk umumnya adalah y = a^x, di mana a adalah basis dan x adalah eksponen.

Logaritma, di sisi lain, adalah operasi matematika yang menemukan eksponen dari suatu bilangan pokok untuk menghasilkan bilangan tertentu.

Dengan kata lain, logaritma menjawab pertanyaan “Pangkat berapa yang harus kita pangkatkan basis a untuk mendapatkan bilangan b?”.

Secara matematis, hubungan ini dapat ditulis sebagai:

log_a b = x jika dan hanya jika a^x = b.

Contoh Penerapan Logaritma dalam Menyelesaikan Persamaan Eksponensial

Misalnya, kita memiliki persamaan eksponensial: 2^x = 8. Untuk menyelesaikan persamaan ini, kita dapat menggunakan logaritma.

Dengan mengambil logaritma kedua ruas dengan basis 2, kita mendapatkan:

log₂ 2^x = log₂ 8.

Karena log_a a^x = x, maka persamaan di atas dapat disederhanakan menjadi:

x = log₂ 8.

Karena 2³ = 8, maka log₂ 8 = 3.

Jadi, solusi dari persamaan 2^x = 8 adalah x = 3.

Hubungan Timbal Balik Antara Fungsi Eksponensial dan Logaritma

Berikut tabel yang menunjukkan hubungan timbal balik antara fungsi logaritma dan fungsi eksponensial:

Fungsi Eksponensial	Fungsi Logaritma
y = ax	x = loga y

Dari tabel di atas, dapat dilihat bahwa fungsi logaritma adalah invers dari fungsi eksponensial. Ini berarti bahwa jika kita memasukkan nilai y ke dalam fungsi logaritma dengan basis a, kita akan mendapatkan nilai x yang sama dengan nilai x yang akan kita dapatkan jika kita memasukkan nilai x ke dalam fungsi eksponensial dengan basis a.

Pentingnya Memahami Hubungan Logaritma dan Fungsi Eksponensial

Memahami hubungan antara logaritma dan fungsi eksponensial sangat penting dalam berbagai bidang, seperti:

• Matematika: Logaritma digunakan untuk menyelesaikan persamaan eksponensial, menghitung nilai logaritma, dan mempelajari fungsi eksponensial.
• Fisika: Logaritma digunakan untuk mengukur intensitas suara, gempa bumi, dan kekuatan bintang.
• Kimia: Logaritma digunakan untuk menghitung pH larutan, dan konsentrasi ion.
• Biologi: Logaritma digunakan untuk mempelajari pertumbuhan populasi dan laju reaksi kimia.
• Ekonomi: Logaritma digunakan untuk menganalisis pertumbuhan ekonomi, inflasi, dan nilai aset.

Kesimpulan

Logaritma dan fungsi eksponensial adalah konsep matematika yang saling terkait erat. Memahami hubungan antara keduanya sangat penting untuk memahami berbagai fenomena alam dan menyelesaikan masalah dalam berbagai bidang ilmu pengetahuan dan teknologi.

Ulasan Penutup

Setelah mempelajari contoh soal logaritma penjumlahan dan pengurangan, kita dapat melihat bahwa konsep logaritma tidak hanya menarik secara teoritis tetapi juga memiliki aplikasi praktis dalam berbagai bidang. Dengan memahami sifat-sifat logaritma dan strategi penyelesaian yang tepat, kita dapat menguasai operasi logaritma dan memecahkan masalah yang lebih kompleks.