Contoh Soal Median, Modus, dan Mean: Uji Pemahaman Statistik Anda

Contoh soal median modus mean – Median, modus, dan mean adalah tiga konsep dasar dalam statistika yang sering kita temui dalam kehidupan sehari-hari. Ketiganya membantu kita memahami data dan mengungkap tren, pola, dan nilai tengah dari kumpulan data. Median adalah nilai tengah dari data yang telah diurutkan, modus adalah nilai yang paling sering muncul, dan mean adalah rata-rata dari semua data. Dengan memahami konsep ini, kita dapat menganalisis berbagai macam informasi, seperti data penjualan, hasil ujian, atau bahkan data cuaca.

Dalam artikel ini, kita akan menjelajahi contoh soal median, modus, dan mean yang akan membantu Anda memahami konsep ini dengan lebih baik. Kita akan membahas berbagai contoh soal, mulai dari soal dasar hingga soal yang lebih kompleks, yang akan menguji pemahaman Anda tentang ketiga konsep ini. Selain itu, kita juga akan melihat bagaimana median, modus, dan mean digunakan dalam berbagai bidang, seperti ekonomi, kesehatan, dan sosial.

Pengertian Median, Modus, dan Mean

Dalam dunia statistik, median, modus, dan mean merupakan tiga ukuran tendensi sentral yang sering digunakan untuk menggambarkan data. Ketiga ukuran ini memberikan gambaran umum tentang nilai pusat dari sekumpulan data. Meskipun ketiganya mengukur kecenderungan sentral, masing-masing memiliki cara menghitung dan interpretasi yang berbeda.

Pengertian Median

Median adalah nilai tengah dari suatu set data yang telah diurutkan dari yang terkecil hingga yang terbesar. Median membagi data menjadi dua bagian yang sama besar, di mana 50% data berada di bawah median dan 50% lainnya berada di atas median.

Contoh sederhana: Misalnya, kita memiliki data set nilai ujian berikut: 70, 80, 85, 90, 95. Median dari data set ini adalah 85, karena merupakan nilai tengah setelah data diurutkan.

Pengertian Modus

Modus adalah nilai yang paling sering muncul dalam suatu set data. Modus dapat digunakan untuk mengidentifikasi nilai yang paling umum atau populer dalam data.

Contoh sederhana: Misalnya, kita memiliki data set warna mobil yang dijual di suatu dealer: Merah, Biru, Merah, Hijau, Biru, Merah. Modus dari data set ini adalah Merah, karena warna Merah muncul paling sering.

Pengertian Mean

Mean adalah rata-rata dari suatu set data. Mean dihitung dengan menjumlahkan semua nilai dalam data set dan membaginya dengan jumlah nilai dalam data set.

Contoh sederhana: Misalnya, kita memiliki data set tinggi badan siswa: 160 cm, 170 cm, 175 cm, 180 cm. Mean dari data set ini adalah (160 + 170 + 175 + 180) / 4 = 171,25 cm.

Perbandingan Median, Modus, dan Mean

Konsep	Definisi	Cara Menghitung	Contoh Penerapan
Median	Nilai tengah dari suatu set data yang telah diurutkan.	Urutkan data dari yang terkecil hingga yang terbesar. Median adalah nilai tengah.	Menentukan nilai tengah dari data gaji karyawan, nilai ujian siswa, atau tinggi badan siswa.
Modus	Nilai yang paling sering muncul dalam suatu set data.	Hitung frekuensi kemunculan setiap nilai. Modus adalah nilai dengan frekuensi tertinggi.	Menentukan ukuran sepatu yang paling banyak terjual, warna mobil yang paling banyak dipesan, atau jenis makanan yang paling banyak dipesan di restoran.
Mean	Rata-rata dari suatu set data.	Jumlahkan semua nilai dalam data set dan bagi dengan jumlah nilai dalam data set.	Menghitung rata-rata nilai ujian siswa, rata-rata pendapatan keluarga, atau rata-rata suhu harian.

Cara Menghitung Median, Modus, dan Mean

Median, modus, dan mean merupakan ukuran pemusatan data yang penting dalam statistika. Ketiga ukuran ini memberikan gambaran tentang nilai tengah atau nilai yang paling sering muncul dalam suatu kumpulan data. Masing-masing memiliki cara perhitungan yang berbeda dan memberikan informasi yang berbeda pula.

Cara Menghitung Median

Median adalah nilai tengah dalam suatu kumpulan data yang telah diurutkan dari yang terkecil hingga yang terbesar. Cara menghitung median tergantung pada apakah data tersebut tunggal atau kelompok.

Median Data Tunggal

Untuk data tunggal, langkah-langkah menghitung median adalah sebagai berikut:

1. Urutkan data dari yang terkecil hingga yang terbesar.
2. Jika jumlah data ganjil, median adalah nilai tengah. Misalnya, median dari data 2, 4, 5, 7, 9 adalah 5.
3. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah. Misalnya, median dari data 2, 4, 5, 7 adalah (4+5)/2 = 4.5.

Median Data Kelompok

Untuk data kelompok, langkah-langkah menghitung median adalah sebagai berikut:

1. Tentukan kelas median, yaitu kelas yang memuat nilai tengah data.
2. Hitung frekuensi kumulatif (fk) untuk setiap kelas.
3. Tentukan frekuensi kumulatif sebelum kelas median (fk_b).
4. Hitung frekuensi kelas median (f_m).
5. Tentukan batas bawah kelas median (b_m).
6. Hitung panjang kelas (p).
7. Hitung median dengan rumus:

Median = b_m + [(n/2 – fk_b)/f_m] x p

Cara Menghitung Modus

Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data. Cara menghitung modus tergantung pada apakah data tersebut tunggal atau kelompok.

Modus Data Tunggal

Untuk data tunggal, modus adalah nilai yang paling sering muncul. Misalnya, modus dari data 2, 4, 5, 5, 7, 9 adalah 5.

Modus Data Kelompok

Untuk data kelompok, modus adalah nilai tengah dari kelas yang memiliki frekuensi terbanyak. Langkah-langkah menghitung modus adalah sebagai berikut:

1. Tentukan kelas modus, yaitu kelas yang memiliki frekuensi terbanyak.
2. Tentukan batas bawah kelas modus (b_m).
3. Hitung frekuensi kelas modus (f_m).
4. Hitung frekuensi kelas sebelum kelas modus (f₁).
5. Hitung frekuensi kelas setelah kelas modus (f₂).
6. Hitung panjang kelas (p).
7. Hitung modus dengan rumus:

Modus = b_m + [(f_m – f₁) / (2f_m – f₁ – f₂)] x p

Cara Menghitung Mean

Mean adalah rata-rata dari semua nilai dalam suatu kumpulan data. Cara menghitung mean tergantung pada apakah data tersebut tunggal atau kelompok.

Mean Data Tunggal

Untuk data tunggal, mean dihitung dengan menjumlahkan semua nilai data dan membaginya dengan jumlah data. Misalnya, mean dari data 2, 4, 5, 7, 9 adalah (2+4+5+7+9)/5 = 5.4.

Mean Data Kelompok

Untuk data kelompok, mean dihitung dengan menggunakan rumus:

Mean = Σ(f_i x x_i) / Σf_i

di mana:

• f_i adalah frekuensi kelas ke-i
• x_i adalah titik tengah kelas ke-i

Aplikasi Median, Modus, dan Mean dalam Kehidupan Sehari-hari

Median, modus, dan mean adalah tiga ukuran tendensi sentral yang umum digunakan dalam statistik. Ketiganya memberikan informasi yang berbeda tentang distribusi data, dan aplikasi masing-masing sangat bergantung pada konteks dan tujuan analisis. Dalam kehidupan sehari-hari, kita seringkali tanpa sadar menggunakan konsep-konsep ini untuk memahami berbagai fenomena, baik dalam bidang ekonomi, kesehatan, maupun sosial.

Contoh Aplikasi Median, Modus, dan Mean dalam Berbagai Bidang

Berikut beberapa contoh aplikasi median, modus, dan mean dalam berbagai bidang:

• Ekonomi:
• Median Pendapatan: Median pendapatan digunakan untuk mengukur pendapatan tengah dari suatu populasi. Median lebih baik digunakan daripada mean dalam hal ini karena mean dapat dipengaruhi oleh nilai ekstrem, seperti pendapatan miliarder. Median memberikan gambaran yang lebih akurat tentang pendapatan mayoritas penduduk.
• Modus Harga: Modus harga digunakan untuk mengidentifikasi harga produk yang paling sering dijual. Informasi ini dapat membantu penjual dalam menentukan strategi harga yang optimal.
• Mean Pertumbuhan Ekonomi: Mean pertumbuhan ekonomi digunakan untuk mengukur rata-rata pertumbuhan ekonomi suatu negara selama periode tertentu. Informasi ini dapat digunakan untuk menilai kinerja ekonomi suatu negara.
• Kesehatan:
• Median Usia Pasien: Median usia pasien dapat digunakan untuk mengidentifikasi kelompok usia yang paling sering terkena suatu penyakit. Informasi ini dapat membantu para profesional kesehatan dalam mengembangkan strategi pencegahan dan pengobatan yang lebih efektif.
• Modus Gejala: Modus gejala digunakan untuk mengidentifikasi gejala yang paling sering muncul pada pasien dengan suatu penyakit. Informasi ini dapat membantu para profesional kesehatan dalam mendiagnosis penyakit dengan lebih akurat.
• Mean Tekanan Darah: Mean tekanan darah digunakan untuk mengukur rata-rata tekanan darah seseorang. Informasi ini dapat digunakan untuk menilai risiko penyakit jantung dan pembuluh darah.
• Sosial:
• Median Usia Pernikahan: Median usia pernikahan digunakan untuk mengidentifikasi usia rata-rata orang menikah di suatu wilayah. Informasi ini dapat digunakan untuk memahami tren sosial dan budaya terkait pernikahan.
• Modus Pilihan Politik: Modus pilihan politik digunakan untuk mengidentifikasi pilihan politik yang paling banyak dipilih oleh masyarakat. Informasi ini dapat digunakan untuk memahami preferensi politik masyarakat.
• Mean Jumlah Anak: Mean jumlah anak digunakan untuk mengukur rata-rata jumlah anak yang dimiliki oleh keluarga di suatu wilayah. Informasi ini dapat digunakan untuk memahami tren demografi dan perencanaan keluarga.

Perbedaan Median, Modus, dan Mean

Dalam dunia statistik, kita seringkali berhadapan dengan data yang beragam. Untuk memahami pola dan tren dalam data tersebut, kita perlu menggunakan alat yang tepat. Median, modus, dan mean merupakan tiga ukuran tendensi sentral yang umum digunakan dalam analisis data. Meskipun ketiganya memberikan informasi tentang pusat data, namun masing-masing memiliki karakteristik dan kegunaan yang berbeda.

Contoh soal median, modus, dan mean memang sering muncul dalam pelajaran matematika. Namun, kamu juga bisa menemukan soal-soal ini dalam tes assessment, lho! Nah, buat kamu yang sedang mempersiapkan diri untuk tes assessment, coba cek contoh soal dan jawaban tes assessment yang ada di website ini.

Di sana, kamu bisa menemukan berbagai macam soal, termasuk soal median, modus, dan mean, yang bisa kamu gunakan untuk latihan. Dengan latihan yang cukup, kamu akan lebih siap menghadapi tes assessment dan meraih hasil yang memuaskan.

Perbedaan Dasar Median, Modus, dan Mean

Berikut ini adalah penjelasan singkat tentang perbedaan mendasar antara median, modus, dan mean:

• Median adalah nilai tengah dari suatu set data yang telah diurutkan. Untuk menemukan median, kita perlu mengurutkan data dari yang terkecil hingga yang terbesar, lalu mengambil nilai tengah. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
• Modus adalah nilai yang paling sering muncul dalam suatu set data. Dalam suatu set data, nilai yang muncul paling banyak disebut modus. Sebuah set data dapat memiliki satu modus (unimodal), dua modus (bimodal), atau lebih dari dua modus (multimodal).
• Mean adalah rata-rata dari semua nilai dalam suatu set data. Untuk menghitung mean, kita menjumlahkan semua nilai dalam set data, kemudian membaginya dengan jumlah data.

Kapan Menggunakan Median, Modus, atau Mean

Pilihan penggunaan median, modus, atau mean tergantung pada jenis data dan tujuan analisis. Berikut adalah beberapa panduan:

• Median lebih baik digunakan ketika data mengandung outlier atau nilai ekstrem. Median tidak terpengaruh oleh nilai ekstrem, sehingga memberikan gambaran yang lebih akurat tentang pusat data dibandingkan mean. Contohnya, dalam data pendapatan rumah tangga, median lebih baik digunakan daripada mean karena adanya beberapa rumah tangga dengan pendapatan yang sangat tinggi yang dapat memengaruhi nilai mean.
• Modus berguna untuk data kategorikal atau data diskrit. Modus menunjukkan nilai yang paling populer atau paling sering muncul dalam data. Misalnya, dalam data warna mobil yang terjual, modus menunjukkan warna mobil yang paling banyak dibeli.
• Mean lebih baik digunakan ketika data terdistribusi normal dan tidak mengandung outlier. Mean memberikan gambaran yang baik tentang pusat data dan merupakan ukuran yang umum digunakan dalam banyak analisis statistik.

Contoh Perbedaan Signifikan Median, Modus, dan Mean

Perhatikan data berikut yang menunjukkan skor ujian 10 siswa:

Siswa	Skor
A	60
B	70
C	75
D	80
E	85
F	90
G	95
H	100
I	100
J	100

Dalam data ini, mean adalah 85, median adalah 87.5, dan modus adalah 100. Mean terpengaruh oleh nilai ekstrem (100), sedangkan median dan modus memberikan gambaran yang lebih akurat tentang pusat data. Dalam kasus ini, median dan modus lebih baik digunakan daripada mean untuk menggambarkan skor ujian siswa.

Kelebihan dan Kekurangan Median, Modus, dan Mean: Contoh Soal Median Modus Mean

Dalam analisis data, kita seringkali menggunakan ukuran pemusatan data untuk memahami distribusi data. Ukuran pemusatan data yang umum digunakan adalah median, modus, dan mean. Ketiga ukuran ini memiliki kelebihan dan kekurangan masing-masing, dan pemilihannya bergantung pada jenis data dan tujuan analisis. Berikut adalah penjelasan mengenai kelebihan dan kekurangan masing-masing ukuran pemusatan data.

Median

Median adalah nilai tengah dari data yang telah diurutkan. Median tidak dipengaruhi oleh outlier, yaitu nilai ekstrem yang jauh dari nilai lainnya dalam data.

• Kelebihan Median:
• Tidak dipengaruhi oleh outlier, sehingga lebih stabil dalam data yang mengandung outlier.
• Mudah dihitung dan dipahami.
• Memberikan representasi yang lebih akurat dari pusat data dalam data yang miring (skewed data).
• Kekurangan Median:
• Tidak memperhitungkan semua nilai dalam data, sehingga tidak mewakili semua data secara keseluruhan.
• Kurang sensitif terhadap perubahan kecil dalam data.

Contoh kasus: Jika kita ingin mengetahui gaji rata-rata karyawan di suatu perusahaan, median mungkin lebih cocok digunakan daripada mean. Karena adanya outlier, seperti gaji direktur yang sangat tinggi, dapat memengaruhi mean gaji. Median akan memberikan gambaran yang lebih akurat tentang gaji rata-rata karyawan, karena tidak dipengaruhi oleh outlier.

Modus

Modus adalah nilai yang paling sering muncul dalam data. Modus sangat berguna untuk data kategorikal, seperti jenis kelamin, warna, atau merek produk.

• Kelebihan Modus:
• Mudah dihitung dan dipahami.
• Memberikan informasi tentang nilai yang paling sering muncul dalam data.
• Cocok untuk data kategorikal.
• Kekurangan Modus:
• Tidak memperhitungkan semua nilai dalam data.
• Tidak sensitif terhadap perubahan kecil dalam data.
• Tidak selalu ada atau bisa lebih dari satu modus.

Contoh kasus: Jika kita ingin mengetahui warna mobil yang paling banyak dipesan di suatu dealer, modus akan menjadi ukuran yang tepat. Modus akan menunjukkan warna mobil yang paling populer di antara pelanggan.

Mean

Mean adalah nilai rata-rata dari semua nilai dalam data. Mean adalah ukuran pemusatan data yang paling umum digunakan, tetapi juga yang paling rentan terhadap outlier.

• Kelebihan Mean:
• Memperhitungkan semua nilai dalam data.
• Sensitif terhadap perubahan kecil dalam data.
• Mudah dihitung dan dipahami.
• Kekurangan Mean:
• Dipengaruhi oleh outlier, sehingga tidak akurat dalam data yang mengandung outlier.
• Tidak cocok untuk data yang miring (skewed data).

Contoh kasus: Jika kita ingin mengetahui nilai rata-rata ujian siswa dalam suatu kelas, mean mungkin tidak cocok digunakan jika ada beberapa siswa yang mendapatkan nilai sangat rendah. Mean akan dipengaruhi oleh nilai-nilai rendah tersebut dan tidak akan mencerminkan nilai rata-rata kelas secara akurat. Median mungkin lebih cocok digunakan dalam kasus ini.

Tabel Perbandingan, Contoh soal median modus mean

Ukuran Pemusatan Data	Kelebihan	Kekurangan
Median	Tidak dipengaruhi oleh outlier, mudah dihitung, representasi yang lebih akurat dalam data yang miring	Tidak memperhitungkan semua nilai, kurang sensitif terhadap perubahan kecil
Modus	Mudah dihitung, memberikan informasi tentang nilai yang paling sering muncul, cocok untuk data kategorikal	Tidak memperhitungkan semua nilai, tidak sensitif terhadap perubahan kecil, tidak selalu ada atau bisa lebih dari satu modus
Mean	Memperhitungkan semua nilai, sensitif terhadap perubahan kecil, mudah dihitung	Dipengaruhi oleh outlier, tidak cocok untuk data yang miring

Soal Latihan Median, Modus, dan Mean

Median, modus, dan mean adalah tiga ukuran tendensi sentral yang umum digunakan dalam statistik. Ketiga ukuran ini membantu kita memahami data dengan memberikan informasi tentang titik tengah, nilai yang paling sering muncul, dan nilai rata-rata dari sekumpulan data.

Berikut ini beberapa soal latihan yang dapat membantu kamu memahami konsep median, modus, dan mean:

Soal Latihan Median, Modus, dan Mean

Berikut adalah beberapa soal latihan tentang median, modus, dan mean. Cobalah untuk mengerjakannya sendiri sebelum melihat kunci jawaban!

1. Tentukan median dari data berikut: 2, 4, 6, 8, 10.

2. Tentukan modus dari data berikut: 1, 2, 2, 3, 3, 3, 4, 4, 5.

3. Tentukan mean dari data berikut: 10, 15, 20, 25, 30.

4. Seorang pedagang menjual 10 buah apel dengan harga Rp 2.000,- per buah. Jika dia menjual 5 buah apel dengan harga Rp 1.500,- per buah, berapa rata-rata harga jual apel tersebut?

5. Suatu kelas terdiri dari 30 siswa. Nilai ulangan matematika mereka adalah sebagai berikut: 7, 8, 6, 9, 7, 8, 7, 8, 9, 7, 8, 7, 8, 9, 7, 8, 7, 8, 9, 7, 8, 7, 8, 9, 7, 8, 7, 8, 9, 7. Tentukan median, modus, dan mean dari nilai ulangan matematika tersebut.

Kunci Jawaban

Berikut adalah kunci jawaban untuk soal latihan di atas:

1. Median dari data 2, 4, 6, 8, 10 adalah 6.

2. Modus dari data 1, 2, 2, 3, 3, 3, 4, 4, 5 adalah 3.

3. Mean dari data 10, 15, 20, 25, 30 adalah 20.

4. Rata-rata harga jual apel tersebut adalah Rp 1.750,-.

5. Median dari nilai ulangan matematika tersebut adalah 8. Modus dari nilai ulangan matematika tersebut adalah 8. Mean dari nilai ulangan matematika tersebut adalah 7,8.

Contoh Soal Median, Modus, dan Mean dalam Ujian

Median, modus, dan mean merupakan tiga ukuran pemusatan data yang sering muncul dalam ujian matematika. Ketiga ukuran ini memiliki cara perhitungan yang berbeda dan digunakan untuk menggambarkan karakteristik data yang berbeda pula.

Berikut ini adalah beberapa contoh soal median, modus, dan mean yang sering muncul dalam ujian, beserta langkah-langkah penyelesaiannya.

Median

Median merupakan nilai tengah dari suatu data yang telah diurutkan dari yang terkecil hingga yang terbesar. Untuk menentukan median, perlu diperhatikan apakah jumlah data ganjil atau genap.

• Jika jumlah data ganjil, median adalah nilai tengah data yang telah diurutkan.
• Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah data yang telah diurutkan.

Contoh Soal:

Tentukan median dari data berikut:

2, 5, 8, 1, 3, 7, 9

Penyelesaian:

1. Urutkan data dari yang terkecil hingga yang terbesar:

1, 2, 3, 5, 7, 8, 9

2. Karena jumlah data ganjil (7), maka median adalah nilai tengah, yaitu 5.

Jadi, median dari data tersebut adalah 5.

Modus

Modus merupakan nilai yang paling sering muncul dalam suatu data. Data dapat memiliki satu modus, lebih dari satu modus, atau tidak memiliki modus.

Contoh Soal:

Tentukan modus dari data berikut:

10, 12, 15, 10, 12, 18, 12, 15

Penyelesaian:

1. Identifikasi nilai yang paling sering muncul dalam data.

2. Nilai 12 muncul sebanyak 3 kali, sedangkan nilai lainnya muncul kurang dari 3 kali.

Jadi, modus dari data tersebut adalah 12.

Mean

Mean merupakan rata-rata dari semua nilai dalam suatu data. Mean dihitung dengan menjumlahkan semua nilai data, kemudian dibagi dengan jumlah data.

Contoh Soal:

Tentukan mean dari data berikut:

4, 6, 8, 10, 12

Penyelesaian:

1. Jumlahkan semua nilai data:

4 + 6 + 8 + 10 + 12 = 40

2. Bagi jumlah data dengan jumlah nilai data:

40 / 5 = 8

Jadi, mean dari data tersebut adalah 8.

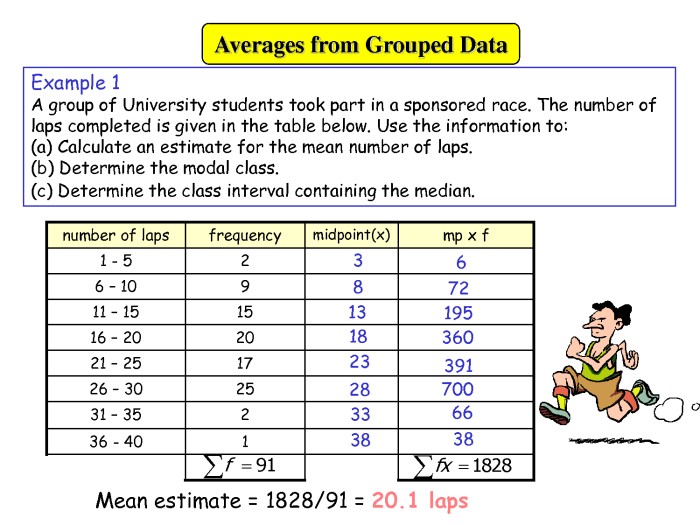
Ilustrasi Median, Modus, dan Mean dalam Grafik

Untuk memahami konsep median, modus, dan mean dengan lebih baik, kita bisa mengilustrasikannya dalam bentuk grafik. Grafik dapat memberikan gambaran visual yang jelas tentang bagaimana ketiga ukuran tendensi sentral ini bekerja dan bagaimana mereka dapat berbeda dalam satu set data.

Ilustrasi Grafik

Bayangkan kita memiliki data tentang tinggi badan siswa dalam satu kelas. Kita dapat membuat histogram untuk menggambarkan distribusi data ini. Histogram adalah grafik batang yang menunjukkan frekuensi setiap rentang tinggi badan.

Dalam histogram, kita dapat mengidentifikasi:

• Mean: Titik keseimbangan dari data. Ini dapat dibayangkan sebagai titik di mana histogram akan seimbang jika kita meletakkannya di atas titik itu. Mean dihitung dengan menjumlahkan semua nilai data dan membaginya dengan jumlah nilai data.
• Median: Nilai tengah dari data yang telah diurutkan. Dalam histogram, median adalah titik yang membagi data menjadi dua bagian yang sama. Separuh data berada di atas median, dan separuh lainnya berada di bawahnya.
• Modus: Nilai yang paling sering muncul dalam data. Dalam histogram, modus adalah batang tertinggi, yang menunjukkan rentang tinggi badan yang paling banyak muncul di kelas.

Contohnya, jika histogram menunjukkan bahwa rentang tinggi badan 160-165 cm memiliki frekuensi tertinggi, maka modus berada di rentang tersebut. Median adalah titik di mana jumlah siswa yang lebih pendek sama dengan jumlah siswa yang lebih tinggi. Mean adalah titik keseimbangan dari histogram.

Interpretasi Grafik

Dengan mengamati grafik, kita dapat melihat bahwa:

• Mean, median, dan modus dapat memiliki nilai yang sama, tetapi tidak selalu. Dalam distribusi data simetris, ketiga ukuran tendensi sentral ini akan bertepatan.
• Dalam distribusi data yang miring (asimetris), mean, median, dan modus akan berbeda. Misalnya, jika data miring ke kanan, mean akan lebih besar dari median, dan median akan lebih besar dari modus.
• Median dan modus lebih tahan terhadap outlier (nilai ekstrem) daripada mean. Ini karena mean dipengaruhi oleh nilai ekstrem, sedangkan median dan modus tidak.

Dengan memahami hubungan antara mean, median, dan modus dalam grafik, kita dapat memperoleh pemahaman yang lebih mendalam tentang karakteristik data dan interpretasi yang tepat.

Hubungan Median, Modus, dan Mean

Dalam analisis data, median, modus, dan mean merupakan ukuran tendensi sentral yang penting untuk menggambarkan karakteristik kumpulan data. Ketiga ukuran ini memberikan informasi yang berbeda tentang titik tengah data, dan pemahaman tentang hubungan di antara mereka dapat memberikan wawasan yang lebih dalam tentang distribusi data.

Pengertian Median, Modus, dan Mean

Median, modus, dan mean adalah tiga ukuran tendensi sentral yang digunakan untuk menggambarkan karakteristik kumpulan data. Ketiga ukuran ini memberikan informasi yang berbeda tentang titik tengah data, dan pemahaman tentang hubungan di antara mereka dapat memberikan wawasan yang lebih dalam tentang distribusi data.

• Median adalah nilai tengah dari kumpulan data yang telah diurutkan. Untuk menemukan median, urutkan data dari yang terkecil hingga yang terbesar, lalu temukan nilai tengah. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
• Modus adalah nilai yang paling sering muncul dalam kumpulan data. Dalam beberapa kasus, kumpulan data mungkin tidak memiliki modus, atau mungkin memiliki lebih dari satu modus.
• Mean adalah rata-rata dari semua nilai dalam kumpulan data. Untuk menghitung mean, jumlahkan semua nilai dalam kumpulan data dan bagi dengan jumlah total nilai.

Hubungan Antara Median, Modus, dan Mean

Hubungan antara median, modus, dan mean dapat memberikan informasi tentang bentuk distribusi data. Berikut adalah beberapa poin penting tentang hubungan antara ketiga ukuran tersebut:

• Distribusi Simetris: Dalam distribusi simetris, median, modus, dan mean akan bernilai sama. Ini berarti bahwa data terdistribusi secara merata di sekitar titik tengah.
• Distribusi Skew Kanan: Dalam distribusi skew kanan, mean akan lebih besar daripada median, dan median akan lebih besar daripada modus. Ini berarti bahwa sebagian besar data berada di sisi kiri distribusi, dan ada beberapa nilai ekstrem di sisi kanan.
• Distribusi Skew Kiri: Dalam distribusi skew kiri, mean akan lebih kecil daripada median, dan median akan lebih kecil daripada modus. Ini berarti bahwa sebagian besar data berada di sisi kanan distribusi, dan ada beberapa nilai ekstrem di sisi kiri.

Contoh Kasus

Misalnya, perhatikan kumpulan data berikut yang menunjukkan skor ujian dari 10 siswa:

Skor Ujian
60
70
75
80
85
90
95
100
100
100

Dalam kasus ini, median adalah 87,5, modus adalah 100, dan mean adalah 85. Karena mean lebih kecil dari median, dan median lebih kecil dari modus, maka distribusi data tersebut adalah skew kiri.

Diagram Hubungan Median, Modus, dan Mean

Diagram berikut menunjukkan hubungan antara median, modus, dan mean dalam berbagai bentuk distribusi:

[Gambar diagram yang menunjukkan hubungan antara median, modus, dan mean dalam distribusi simetris, skew kanan, dan skew kiri]

Diagram ini menunjukkan bahwa posisi relatif dari median, modus, dan mean dapat memberikan informasi tentang bentuk distribusi data. Dalam distribusi simetris, ketiga ukuran tersebut akan bernilai sama. Dalam distribusi skew kanan, mean akan lebih besar daripada median, dan median akan lebih besar daripada modus. Dalam distribusi skew kiri, mean akan lebih kecil daripada median, dan median akan lebih kecil daripada modus.

Peranan Median, Modus, dan Mean dalam Statistika



Dalam ilmu statistika, median, modus, dan mean merupakan tiga ukuran pemusatan data yang sangat penting. Ketiganya memberikan gambaran tentang pusat distribusi data, namun dengan cara yang berbeda. Pemahaman yang baik tentang peranan masing-masing ukuran sangat penting dalam analisis data dan pengambilan keputusan yang tepat.

Peranan Median, Modus, dan Mean dalam Analisis Data

Ketiga ukuran ini memberikan informasi yang berbeda tentang data. Median, sebagai nilai tengah data, sangat berguna dalam mengukur nilai tipikal data ketika data terdistribusi secara tidak simetris atau terdapat nilai ekstrem yang dapat mempengaruhi mean. Modus, sebagai nilai yang paling sering muncul, menunjukkan nilai yang paling umum dalam data. Sementara mean, sebagai rata-rata dari semua data, memberikan informasi tentang nilai pusat data secara keseluruhan.

Contoh Kasus Nyata Peranan Median, Modus, dan Mean

Bayangkan kita ingin menganalisis data gaji karyawan di sebuah perusahaan. Data ini mungkin terdistribusi secara tidak simetris, dengan beberapa karyawan memiliki gaji yang sangat tinggi dibandingkan dengan yang lain. Dalam kasus ini, mean mungkin tidak mencerminkan nilai gaji tipikal karyawan. Median, sebagai nilai tengah, akan lebih tepat untuk menggambarkan gaji tipikal karyawan. Modus, di sisi lain, akan menunjukkan rentang gaji yang paling umum di perusahaan.

• Mean digunakan untuk menghitung rata-rata gaji, tetapi mungkin terpengaruh oleh gaji karyawan dengan gaji tinggi.
• Median memberikan gambaran yang lebih akurat tentang gaji tipikal karyawan, karena tidak terpengaruh oleh nilai ekstrem.
• Modus menunjukkan rentang gaji yang paling umum di perusahaan, yang dapat memberikan informasi tentang struktur gaji dan kebijakan perusahaan.

Penggunaan Median, Modus, dan Mean dalam Pengambilan Keputusan

Pemahaman tentang peranan median, modus, dan mean sangat penting dalam pengambilan keputusan yang berdasarkan data. Berikut beberapa contoh:

• Perencanaan anggaran: Mean dapat digunakan untuk memperkirakan total pengeluaran perusahaan. Namun, median mungkin lebih tepat untuk memperkirakan pengeluaran tipikal karyawan. Modus dapat digunakan untuk mengidentifikasi item pengeluaran yang paling umum.
• Analisis pasar: Modus dapat digunakan untuk mengidentifikasi produk yang paling populer di pasar. Median dapat digunakan untuk mengukur nilai tipikal produk di pasar. Mean dapat digunakan untuk menghitung total nilai pasar produk.
• Evaluasi kinerja: Median dapat digunakan untuk mengukur kinerja tipikal karyawan. Modus dapat digunakan untuk mengidentifikasi pola kinerja yang paling umum. Mean dapat digunakan untuk menghitung kinerja keseluruhan karyawan.

Akhir Kata

Dengan memahami konsep median, modus, dan mean, kita dapat memperoleh pemahaman yang lebih dalam tentang data dan mengungkap informasi penting yang tersembunyi di dalamnya. Ketiga konsep ini memiliki peranan penting dalam analisis data dan pengambilan keputusan yang lebih baik. Contoh soal yang telah kita bahas di sini dapat menjadi panduan bagi Anda untuk menguji pemahaman Anda tentang konsep ini. Jangan ragu untuk berlatih dengan soal-soal lain dan terus memperdalam pemahaman Anda tentang statistika.

Sebarkan ini:

Posting terkait:

• 

  Contoh Soal Median, Mean, dan Modus: Pahami Ukuran Pemusatan Data

• 

  Contoh Soal Median dan Jawabannya: Menguak Rahasia Data Tengah

• 

  Contoh Soal Modus dan Median: Pelajari Cara Menghitung dan Penerapannya