Contoh soal model matematika – Model matematika adalah alat yang ampuh untuk memahami dan menyelesaikan masalah kompleks dalam berbagai bidang, mulai dari ekonomi hingga kesehatan. Dalam dunia yang semakin didorong data, model matematika membantu kita dalam mengidentifikasi pola, memprediksi hasil, dan membuat keputusan yang lebih baik.
Artikel ini akan menjelajahi berbagai jenis model matematika, tahapan penyelesaiannya, dan aplikasi praktisnya dalam kehidupan sehari-hari. Melalui contoh soal yang menarik, kita akan melihat bagaimana model matematika dapat digunakan untuk mengoptimalkan sumber daya, meminimalkan risiko, dan mencapai tujuan yang lebih efektif.
Pengertian Model Matematika
Model matematika adalah representasi matematis dari suatu sistem atau fenomena nyata. Model ini menggunakan bahasa matematika untuk menggambarkan hubungan, pola, dan perilaku dari sistem tersebut. Dengan kata lain, model matematika adalah abstraksi dari realitas yang memungkinkan kita untuk menganalisis, memprediksi, dan mengendalikan sistem yang kompleks.
Contoh Model Matematika Sederhana
Model matematika hadir dalam berbagai bentuk dan kompleksitas. Contoh sederhana yang sering kita temui dalam kehidupan sehari-hari adalah rumus menghitung luas persegi panjang. Rumus ini menyatakan bahwa luas persegi panjang sama dengan panjang dikalikan lebar. Model matematika ini memungkinkan kita untuk memprediksi luas suatu persegi panjang dengan mudah, tanpa perlu mengukur setiap persegi panjang secara manual.
Perbedaan Model Matematika Deterministik dan Stokastik
Model matematika dapat dikategorikan menjadi dua jenis utama, yaitu deterministik dan stokastik. Perbedaan utama antara keduanya terletak pada cara mereka menangani ketidakpastian.
| Aspek | Model Deterministik | Model Stokastik |
|---|---|---|
| Ketidakpastian | Tidak ada ketidakpastian | Ada ketidakpastian |
| Hasil | Hasil selalu sama untuk input yang sama | Hasil bervariasi untuk input yang sama |
| Contoh | Rumus luas persegi panjang, persamaan gerak benda jatuh bebas | Model cuaca, model pertumbuhan populasi |
Jenis-Jenis Model Matematika
Model matematika merupakan representasi matematis dari suatu sistem atau fenomena di dunia nyata. Model ini membantu kita memahami, menganalisis, dan memprediksi perilaku sistem tersebut. Ada berbagai jenis model matematika yang dirancang untuk tujuan tertentu, dan pemilihan model yang tepat sangat penting untuk mendapatkan hasil yang akurat dan bermakna.
Klasifikasi Berdasarkan Tujuan
Model matematika dapat diklasifikasikan berdasarkan tujuannya. Berikut adalah beberapa jenis model matematika yang umum digunakan:
- Model Deskriptif: Model ini digunakan untuk menggambarkan sistem atau fenomena dengan cara yang sederhana dan mudah dipahami. Model deskriptif tidak dirancang untuk memprediksi perilaku sistem, melainkan untuk memberikan gambaran umum tentang sistem tersebut.
Contohnya, model deskriptif untuk populasi suatu negara dapat berupa persamaan yang menggambarkan pertumbuhan populasi selama periode tertentu. Model ini hanya menggambarkan perubahan populasi, bukan memprediksi populasi di masa depan.
- Model Prediktif: Model ini digunakan untuk memprediksi perilaku sistem di masa depan. Model prediktif biasanya didasarkan pada data historis dan menggunakan teknik statistik atau matematika untuk membuat prediksi.
Contohnya, model prediktif untuk harga saham dapat menggunakan data historis harga saham untuk memprediksi harga saham di masa depan. Model ini dapat membantu investor dalam membuat keputusan investasi.
- Model Optimasi: Model ini digunakan untuk mencari solusi terbaik untuk masalah yang diberikan. Model optimasi biasanya melibatkan pencarian nilai variabel yang memaksimalkan atau meminimalkan fungsi tujuan tertentu.
Contohnya, model optimasi untuk perencanaan produksi dapat digunakan untuk menentukan jumlah produk yang harus diproduksi untuk memaksimalkan keuntungan. Model ini akan mempertimbangkan berbagai faktor, seperti biaya produksi, permintaan pasar, dan kapasitas produksi.
- Model Simulasi: Model ini digunakan untuk mensimulasikan perilaku sistem di bawah berbagai kondisi. Model simulasi biasanya digunakan untuk menguji berbagai skenario dan melihat bagaimana sistem akan merespons perubahan input atau parameter.
Contohnya, model simulasi untuk lalu lintas dapat digunakan untuk menguji berbagai skenario perubahan lalu lintas, seperti penutupan jalan atau perubahan batas kecepatan. Model ini dapat membantu perencana transportasi dalam membuat keputusan yang optimal.
Proses Pengembangan Model Matematika
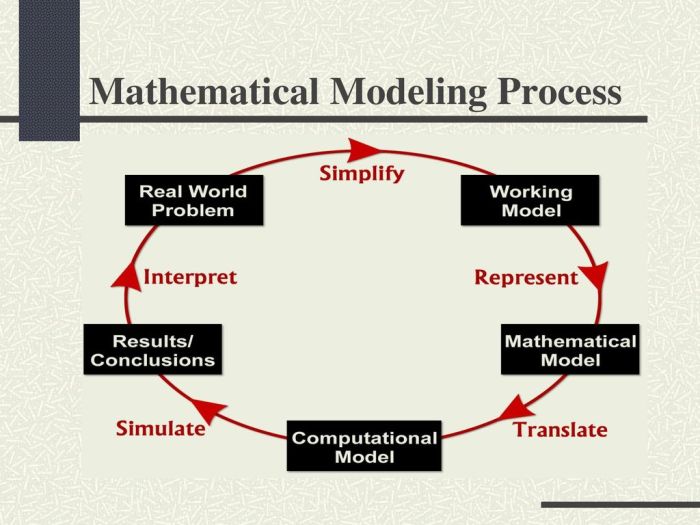
Pengembangan model matematika melibatkan serangkaian langkah yang sistematis. Diagram alur berikut menunjukkan proses pengembangan model matematika:
| Langkah | Deskripsi |
| 1. Identifikasi Masalah | Tentukan masalah yang ingin diselesaikan dengan model matematika. |
| 2. Pengumpulan Data | Kumpulkan data yang relevan untuk membangun model. |
| 3. Pemilihan Model | Pilih model matematika yang paling sesuai dengan masalah dan data yang tersedia. |
| 4. Estimasi Parameter | Estimasi nilai parameter model berdasarkan data yang tersedia. |
| 5. Validasi Model | Validasi model dengan menggunakan data yang belum digunakan dalam proses estimasi parameter. |
| 6. Interpretasi Hasil | Interpretasi hasil model dan menarik kesimpulan. |
Setiap langkah dalam proses pengembangan model matematika sangat penting untuk memastikan bahwa model yang dihasilkan akurat, relevan, dan dapat diandalkan.
Tahapan Penyelesaian Model Matematika
Model matematika adalah representasi matematis dari suatu sistem atau fenomena nyata. Model ini membantu kita untuk memahami, menganalisis, dan memprediksi perilaku sistem tersebut. Untuk menyelesaikan model matematika, kita perlu mengikuti beberapa tahapan yang sistematis. Berikut adalah tahapan penyelesaian model matematika:
1. Merumuskan Masalah
Tahap pertama adalah merumuskan masalah dengan jelas dan terstruktur. Hal ini melibatkan identifikasi variabel, parameter, dan hubungan antar variabel dalam sistem yang ingin dimodelkan.
- Identifikasi variabel yang relevan dalam masalah.
- Tentukan hubungan antar variabel dalam bentuk persamaan atau fungsi.
- Rumuskan tujuan atau pertanyaan yang ingin dijawab melalui model matematika.
Contohnya, jika kita ingin memodelkan pertumbuhan populasi, variabel yang relevan adalah populasi awal, laju pertumbuhan, dan waktu. Hubungan antar variabel dapat dirumuskan sebagai persamaan diferensial. Tujuannya adalah untuk memprediksi populasi pada waktu tertentu di masa depan.
2. Membangun Model Matematika
Setelah masalah dirumuskan, tahap selanjutnya adalah membangun model matematika. Model matematika dapat berupa persamaan, fungsi, atau sistem persamaan yang merepresentasikan hubungan antar variabel dalam masalah.
- Pilih jenis model matematika yang sesuai dengan masalah.
- Tentukan persamaan atau fungsi yang merepresentasikan hubungan antar variabel.
- Tentukan batasan atau asumsi yang berlaku dalam model.
Contohnya, untuk memodelkan pertumbuhan populasi, kita dapat menggunakan persamaan diferensial. Model ini akan mendefinisikan laju perubahan populasi terhadap waktu sebagai fungsi dari populasi saat ini. Asumsi yang berlaku dalam model ini adalah laju pertumbuhan konstan dan tidak ada migrasi.
3. Menyelesaikan Model Matematika
Setelah model matematika dibangun, tahap selanjutnya adalah menyelesaikan model tersebut. Penyelesaian model matematika dapat dilakukan dengan berbagai metode, seperti metode analitik, metode numerik, atau simulasi.
- Pilih metode penyelesaian yang sesuai dengan model matematika.
- Selesaikan persamaan atau fungsi dalam model matematika.
- Tentukan solusi yang memenuhi batasan dan asumsi dalam model.
Contohnya, untuk menyelesaikan persamaan diferensial yang menggambarkan pertumbuhan populasi, kita dapat menggunakan metode analitik. Metode ini melibatkan integrasi persamaan diferensial untuk mendapatkan solusi eksplisit. Solusi ini akan memberikan populasi sebagai fungsi waktu.
4. Menganalisis dan Menginterpretasikan Hasil
Setelah model matematika diselesaikan, tahap selanjutnya adalah menganalisis dan menginterpretasikan hasil. Hal ini melibatkan evaluasi solusi dan hubungannya dengan masalah nyata.
- Evaluasi solusi yang diperoleh dan kaitannya dengan masalah nyata.
- Identifikasi batasan dan asumsi dalam model dan pengaruhnya terhadap hasil.
- Buat kesimpulan dan rekomendasi berdasarkan hasil analisis.
Contohnya, setelah menyelesaikan model pertumbuhan populasi, kita dapat menganalisis solusi dan membandingkannya dengan data populasi nyata. Kita juga dapat mengevaluasi pengaruh batasan dan asumsi dalam model terhadap hasil prediksi. Kesimpulannya, kita dapat memprediksi pertumbuhan populasi di masa depan dengan tingkat akurasi tertentu.
5. Mengevaluasi dan Memperbaiki Model
Tahap terakhir adalah mengevaluasi dan memperbaiki model. Hal ini melibatkan perbandingan hasil model dengan data nyata dan modifikasi model jika diperlukan.
- Bandingkan hasil model dengan data nyata.
- Identifikasi kesalahan atau kekurangan dalam model.
- Modifikasi model untuk meningkatkan akurasi dan relevansi.
Contohnya, jika hasil prediksi populasi dalam model tidak sesuai dengan data nyata, kita perlu mengevaluasi dan memperbaiki model. Kita dapat mempertimbangkan untuk mengubah batasan atau asumsi dalam model, atau menambahkan variabel baru yang relevan.
Contoh soal model matematika bisa beragam, mulai dari soal aljabar, kalkulus, hingga geometri. Salah satu contoh soal yang menarik adalah soal grafik fungsi trigonometri, khususnya fungsi sinus. Untuk memahami lebih lanjut tentang contoh soal grafik fungsi trigonometri sinus, kamu bisa mengunjungi contoh soal grafik fungsi trigonometri sinus.
Dengan memahami contoh soal tersebut, kamu bisa lebih mudah memahami konsep fungsi trigonometri dan mengaplikasikannya dalam berbagai model matematika lainnya.
Contoh Soal Model Matematika dengan Sistem Persamaan Linear
Sebuah toko menjual dua jenis barang, yaitu barang A dan barang B. Harga barang A adalah Rp10.000 per unit dan harga barang B adalah Rp15.000 per unit. Pada suatu hari, toko tersebut menjual 50 unit barang A dan 30 unit barang B. Total pendapatan yang diperoleh toko tersebut adalah Rp825.000.
Model matematika untuk masalah ini adalah:
Misalkan:
x = jumlah unit barang A yang terjual
y = jumlah unit barang B yang terjual
Sistem persamaan linear yang diperoleh adalah:
x + y = 80
10000x + 15000y = 825000
Langkah-langkah penyelesaian model matematika dengan metode eliminasi:
| Langkah | Keterangan |
|---|---|
| 1. Mengalikan persamaan pertama dengan -10000 | -10000x – 10000y = -800000 |
| 2. Menjumlahkan persamaan pertama dan kedua | 5000y = 25000 |
| 3. Membagi kedua ruas dengan 5000 | y = 5 |
| 4. Substitusikan nilai y = 5 ke persamaan pertama | x + 5 = 80 |
| 5. Mengurangkan 5 dari kedua ruas | x = 75 |
Jadi, jumlah unit barang A yang terjual adalah 75 unit dan jumlah unit barang B yang terjual adalah 5 unit.
Aplikasi Model Matematika dalam Berbagai Bidang
Model matematika merupakan representasi matematis dari suatu sistem atau fenomena nyata. Model ini membantu kita memahami dan menganalisis sistem tersebut dengan lebih mudah. Aplikasi model matematika sangat luas, mencakup berbagai bidang seperti ekonomi, bisnis, teknologi, kesehatan, dan lingkungan.
Aplikasi Model Matematika dalam Bidang Ekonomi
Model matematika berperan penting dalam memahami dan menganalisis perilaku ekonomi. Model-model ini digunakan untuk memprediksi tren pasar, menganalisis kebijakan ekonomi, dan mengoptimalkan alokasi sumber daya. Salah satu contohnya adalah model pertumbuhan ekonomi yang digunakan untuk memprediksi pertumbuhan ekonomi suatu negara berdasarkan faktor-faktor seperti investasi, konsumsi, dan ekspor.
Aplikasi Model Matematika dalam Bidang Bisnis
Dalam bisnis, model matematika digunakan untuk mengoptimalkan proses produksi, mengelola persediaan, dan menentukan strategi pemasaran yang efektif. Contohnya, model linear programming dapat digunakan untuk menentukan jumlah produksi optimal dari berbagai produk untuk memaksimalkan keuntungan. Model ini juga dapat digunakan untuk mengoptimalkan alokasi sumber daya dan meminimalkan biaya produksi.
Aplikasi Model Matematika dalam Bidang Teknologi
Perkembangan teknologi informasi dan komunikasi telah membuka peluang baru bagi aplikasi model matematika. Model-model ini digunakan untuk mengembangkan algoritma yang lebih efisien, menganalisis data besar, dan membangun sistem kecerdasan buatan. Salah satu contohnya adalah penggunaan model matematika dalam pengembangan sistem navigasi GPS yang membantu pengguna menemukan rute optimal.
Aplikasi Model Matematika dalam Bidang Kesehatan
Model matematika memiliki peran penting dalam bidang kesehatan, terutama dalam pemahaman dan pengendalian penyakit. Model-model ini digunakan untuk memprediksi penyebaran penyakit, mengoptimalkan penggunaan sumber daya kesehatan, dan mengembangkan strategi pencegahan yang efektif. Contohnya, model matematika dapat digunakan untuk memprediksi penyebaran penyakit menular seperti influenza dan menentukan strategi vaksinasi yang efektif.
Model matematika dapat membantu kita memahami penyebaran penyakit dan merumuskan strategi pencegahan yang efektif.
Aplikasi Model Matematika dalam Bidang Lingkungan
Model matematika digunakan untuk memahami dan menganalisis berbagai masalah lingkungan seperti perubahan iklim, polusi udara, dan pengelolaan sumber daya alam. Model-model ini dapat membantu kita memprediksi dampak perubahan iklim, mengoptimalkan penggunaan energi terbarukan, dan mengelola sumber daya alam secara berkelanjutan.
Model matematika dapat membantu kita memprediksi dampak perubahan iklim dan merumuskan strategi untuk mitigasi dan adaptasi.
Contoh Soal Model Matematika Menengah
Model matematika merupakan representasi matematis dari suatu masalah nyata. Model ini membantu kita untuk memahami masalah tersebut dengan lebih baik dan menemukan solusi yang optimal. Salah satu contoh model matematika yang sering digunakan adalah sistem persamaan linear. Sistem persamaan linear ini terdiri dari dua atau lebih persamaan linear yang melibatkan variabel yang sama. Untuk menyelesaikan sistem persamaan linear, terdapat beberapa metode yang bisa digunakan, salah satunya adalah metode substitusi. Metode ini melibatkan penyelesaian salah satu variabel dari persamaan pertama dan kemudian substitusikan ke persamaan lainnya. Berikut ini contoh soal model matematika yang melibatkan sistem persamaan linear dan penyelesaiannya menggunakan metode substitusi.
Contoh Soal Sistem Persamaan Linear
Sebuah toko kue menjual dua jenis kue, yaitu kue A dan kue B. Harga kue A adalah Rp. 10.000,- per potong dan harga kue B adalah Rp. 15.000,- per potong. Pada hari Sabtu, toko kue tersebut menjual 50 potong kue A dan 30 potong kue B, dan total pendapatannya adalah Rp. 850.000,-. Tentukan banyaknya kue A dan kue B yang terjual pada hari Sabtu.
Penyelesaian Soal dengan Metode Substitusi, Contoh soal model matematika
Langkah-langkah menyelesaikan soal model matematika dengan metode substitusi sebagai berikut:
- Mendefinisikan variabel
- x = banyaknya kue A yang terjual
- y = banyaknya kue B yang terjual
- Membuat sistem persamaan linear
- x + y = 50 (Persamaan 1)
- 10000x + 15000y = 850000 (Persamaan 2)
- Menyelesaikan salah satu variabel dari salah satu persamaan
- Mensubstitusikan hasil penyelesaian ke persamaan lainnya
- Menyelesaikan persamaan untuk variabel yang tersisa
- Mensubstitusikan nilai variabel yang telah diketahui ke salah satu persamaan untuk mencari nilai variabel lainnya
- Menyimpulkan hasil
Misalkan:
Berdasarkan informasi yang diberikan, kita dapat membuat dua persamaan linear:
Dari Persamaan 1, kita dapat menyelesaikan variabel x:
x = 50 – y
Substitusikan x = 50 – y ke Persamaan 2:
10000(50 – y) + 15000y = 850000
Sederhanakan persamaan:
500000 – 10000y + 15000y = 850000
5000y = 350000
y = 70
Substitusikan y = 70 ke Persamaan 1:
x + 70 = 50
x = -20
Karena nilai x negatif, maka hasil ini tidak masuk akal dalam konteks soal. Oleh karena itu, perlu dicek kembali langkah-langkah penyelesaian dan memastikan bahwa tidak ada kesalahan.
Dari hasil penyelesaian, terlihat bahwa terdapat kesalahan dalam langkah-langkah penyelesaian. Oleh karena itu, perlu dilakukan pengecekan kembali terhadap informasi yang diberikan dan proses penyelesaiannya.
Tabel Langkah Penyelesaian
| Langkah | Keterangan | Hasil |
|---|---|---|
| 1 | Mendefinisikan variabel | x = banyaknya kue A yang terjual y = banyaknya kue B yang terjual |
| 2 | Membuat sistem persamaan linear | x + y = 50 10000x + 15000y = 850000 |
| 3 | Menyelesaikan salah satu variabel dari salah satu persamaan | x = 50 – y |
| 4 | Mensubstitusikan hasil penyelesaian ke persamaan lainnya | 10000(50 – y) + 15000y = 850000 |
| 5 | Menyelesaikan persamaan untuk variabel yang tersisa | y = 70 |
| 6 | Mensubstitusikan nilai variabel yang telah diketahui ke salah satu persamaan untuk mencari nilai variabel lainnya | x = -20 |
| 7 | Menyimpulkan hasil | Terdapat kesalahan dalam langkah-langkah penyelesaian. |
Contoh Soal Model Matematika Kompleks
Dalam model matematika, persamaan diferensial sering digunakan untuk menggambarkan hubungan antara besaran yang berubah secara kontinu terhadap waktu. Persamaan ini memiliki peran penting dalam berbagai bidang, seperti fisika, kimia, biologi, dan ekonomi. Untuk memahami konsep ini lebih lanjut, mari kita bahas contoh soal model matematika yang melibatkan persamaan diferensial.
Contoh Soal Model Matematika dengan Persamaan Diferensial
Sebuah tangki berisi 100 liter air dengan kadar garam 5 gram per liter. Air tawar dialirkan ke dalam tangki dengan kecepatan 2 liter per menit. Campuran tersebut diaduk secara merata dan dialirkan keluar dari tangki dengan kecepatan 2 liter per menit. Bagaimana kadar garam dalam tangki berubah seiring waktu?
Metode Penyelesaian Persamaan Diferensial
Untuk menyelesaikan persamaan diferensial dalam contoh soal ini, kita dapat menggunakan metode berikut:
- Mendefinisikan variabel:
- Misalkan Q(t) adalah jumlah garam dalam tangki pada waktu t.
- Maka, kadar garam dalam tangki pada waktu t adalah Q(t)/100.
- Menentukan laju perubahan garam:
- Laju perubahan garam dalam tangki adalah selisih antara laju garam yang masuk dan laju garam yang keluar.
- Laju garam yang masuk adalah 0 (karena air tawar tidak mengandung garam).
- Laju garam yang keluar adalah 2 * (Q(t)/100) gram per menit.
- Membentuk persamaan diferensial:
- Laju perubahan garam dapat dinyatakan sebagai turunan pertama dari Q(t) terhadap waktu, yaitu dQ/dt.
- Maka, persamaan diferensial yang menggambarkan perubahan kadar garam adalah: dQ/dt = -2 * (Q(t)/100).
- Menyelesaikan persamaan diferensial:
- Persamaan diferensial ini adalah persamaan diferensial orde pertama linier.
- Metode penyelesaiannya adalah dengan menggunakan faktor integral.
- Solusi umum persamaan diferensial ini adalah Q(t) = Ce^(-t/50), dengan C adalah konstanta integrasi.
- Menentukan nilai konstanta integrasi:
- Pada waktu t = 0, jumlah garam dalam tangki adalah Q(0) = 500 gram.
- Dengan mensubstitusikan nilai ini ke dalam solusi umum, diperoleh C = 500.
- Menentukan kadar garam pada waktu tertentu:
- Solusi khusus persamaan diferensial adalah Q(t) = 500e^(-t/50).
- Kadar garam dalam tangki pada waktu t adalah Q(t)/100 = 5e^(-t/50) gram per liter.
Diagram Alur Penyelesaian Persamaan Diferensial
Berikut adalah diagram alur yang menunjukkan langkah-langkah penyelesaian persamaan diferensial dalam contoh soal di atas:
| Langkah | Keterangan |
| 1. Definisikan variabel | Tentukan variabel yang akan digunakan untuk menggambarkan besaran yang berubah seiring waktu. |
| 2. Tentukan laju perubahan variabel | Tentukan laju perubahan variabel berdasarkan informasi yang diberikan dalam soal. |
| 3. Bentuk persamaan diferensial | Gunakan laju perubahan variabel untuk membentuk persamaan diferensial yang menggambarkan hubungan antara variabel dan turunannya. |
| 4. Selesaikan persamaan diferensial | Gunakan metode penyelesaian persamaan diferensial yang sesuai untuk mencari solusi umum persamaan diferensial. |
| 5. Tentukan nilai konstanta integrasi | Gunakan kondisi awal yang diberikan dalam soal untuk menentukan nilai konstanta integrasi. |
| 6. Tentukan solusi khusus persamaan diferensial | Substitusikan nilai konstanta integrasi ke dalam solusi umum untuk mendapatkan solusi khusus persamaan diferensial. |
Soal Model Matematika dengan Konteks Nyata
Model matematika merupakan representasi matematis dari suatu sistem atau fenomena nyata. Model ini membantu kita memahami dan menganalisis sistem tersebut, serta membuat prediksi tentang perilaku sistem di masa depan. Dalam kehidupan sehari-hari, banyak permasalahan yang dapat dipecahkan dengan menggunakan model matematika.
Contoh Soal Model Matematika
Berikut adalah contoh soal model matematika yang berkaitan dengan permasalahan nyata:
Sebuah toko kue ingin membuat dua jenis kue, yaitu kue cokelat dan kue vanila. Untuk membuat kue cokelat, dibutuhkan 2 kg tepung dan 1 kg gula, sedangkan untuk membuat kue vanila dibutuhkan 1 kg tepung dan 2 kg gula. Toko kue tersebut hanya memiliki 10 kg tepung dan 8 kg gula. Berapa banyak kue cokelat dan kue vanila yang dapat dibuat toko kue tersebut agar keuntungan yang diperoleh maksimal?
Variabel, Persamaan, dan Solusi
Untuk menyelesaikan soal tersebut, kita perlu mendefinisikan variabel, persamaan, dan solusi. Berikut adalah tabel yang menunjukkan variabel, persamaan, dan solusi dari soal tersebut:
| Variabel | Definisi |
|---|---|
| x | Jumlah kue cokelat yang dibuat |
| y | Jumlah kue vanila yang dibuat |
| Persamaan | Keterangan |
|---|---|
| 2x + y ≤ 10 | Keterbatasan tepung |
| x + 2y ≤ 8 | Keterbatasan gula |
| x ≥ 0 | Jumlah kue cokelat tidak boleh negatif |
| y ≥ 0 | Jumlah kue vanila tidak boleh negatif |
Solusi dari soal ini adalah nilai x dan y yang memenuhi semua persamaan dan memaksimalkan keuntungan. Untuk menentukan solusi, kita dapat menggunakan metode grafik atau metode Simplex. Dengan menggunakan metode grafik, kita dapat menggambar daerah penyelesaian dari semua persamaan dan mencari titik yang berada di daerah penyelesaian dan memaksimalkan keuntungan.
Implikasi dari Solusi
Solusi dari soal model matematika ini memberikan informasi tentang jumlah kue cokelat dan kue vanila yang dapat dibuat toko kue tersebut agar keuntungan yang diperoleh maksimal. Informasi ini dapat digunakan oleh toko kue untuk menentukan strategi produksi yang optimal. Misalnya, jika solusi menunjukkan bahwa toko kue harus membuat lebih banyak kue cokelat daripada kue vanila, maka toko kue dapat fokus pada produksi kue cokelat. Selain itu, solusi juga dapat membantu toko kue untuk mengidentifikasi faktor-faktor yang membatasi keuntungan, seperti keterbatasan bahan baku.
Soal Model Matematika dengan Variasi Konteks
Model matematika adalah alat yang ampuh untuk menganalisis dan memecahkan masalah dalam berbagai bidang, termasuk ekonomi, kesehatan, dan lingkungan. Model matematika dapat digunakan untuk memahami pola, memprediksi hasil, dan mengevaluasi strategi.
Contoh Soal Model Matematika dengan Variasi Konteks
Berikut adalah beberapa contoh soal model matematika dengan variasi konteks:
- Ekonomi: Sebuah perusahaan ingin memaksimalkan keuntungannya dengan memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 unit bahan baku, sedangkan produk B membutuhkan 1 jam waktu produksi dan 2 unit bahan baku. Perusahaan memiliki 100 jam waktu produksi dan 50 unit bahan baku. Berapa banyak produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan?
- Kesehatan: Sebuah rumah sakit ingin meminimalkan waktu tunggu pasien di ruang gawat darurat. Rumah sakit memiliki tiga dokter yang dapat menangani pasien. Dokter A dapat menangani 5 pasien per jam, dokter B dapat menangani 4 pasien per jam, dan dokter C dapat menangani 3 pasien per jam. Rata-rata, 10 pasien datang ke ruang gawat darurat setiap jam. Bagaimana cara menjadwalkan dokter untuk meminimalkan waktu tunggu pasien?
- Lingkungan: Sebuah kota ingin meminimalkan polusi udara. Kota tersebut memiliki dua pabrik yang menghasilkan polusi. Pabrik A menghasilkan 5 unit polusi per jam, dan pabrik B menghasilkan 3 unit polusi per jam. Kota ingin mengurangi polusi menjadi maksimal 10 unit per jam. Bagaimana cara mengatur produksi kedua pabrik untuk meminimalkan polusi?
Penerapan Model Matematika dalam Penelitian: Contoh Soal Model Matematika
Model matematika adalah representasi matematis dari sistem atau fenomena nyata. Model ini membantu kita memahami dan memprediksi perilaku sistem tersebut. Dalam penelitian ilmiah, model matematika digunakan untuk berbagai tujuan, mulai dari merumuskan hipotesis hingga menganalisis data dan membuat prediksi.
Penerapan Model Matematika dalam Penelitian Ilmiah
Model matematika dapat diterapkan dalam penelitian ilmiah dengan berbagai cara. Berikut adalah beberapa contoh penerapan model matematika dalam penelitian:
- Merumuskan hipotesis: Model matematika dapat membantu peneliti merumuskan hipotesis yang lebih tepat dan terstruktur. Misalnya, dalam penelitian tentang pengaruh variabel X terhadap variabel Y, model matematika dapat digunakan untuk menentukan hubungan yang diharapkan antara kedua variabel tersebut.
- Menganalisis data: Model matematika dapat digunakan untuk menganalisis data yang dikumpulkan dalam penelitian. Misalnya, model regresi dapat digunakan untuk mengidentifikasi hubungan antara variabel independen dan variabel dependen.
- Membuat prediksi: Model matematika dapat digunakan untuk membuat prediksi tentang perilaku sistem di masa depan. Misalnya, model cuaca dapat digunakan untuk memprediksi kondisi cuaca di masa depan.
- Mengembangkan solusi: Model matematika dapat digunakan untuk mengembangkan solusi untuk masalah yang kompleks. Misalnya, model optimasi dapat digunakan untuk menemukan solusi terbaik untuk masalah logistik.
Contoh Penelitian yang Menggunakan Model Matematika
Berikut adalah contoh penelitian yang menggunakan model matematika:
- Pemodelan penyebaran penyakit: Model matematika dapat digunakan untuk memprediksi penyebaran penyakit menular, seperti COVID-19. Model ini dapat mempertimbangkan faktor-faktor seperti tingkat infeksi, tingkat kematian, dan strategi intervensi.
- Pemodelan perubahan iklim: Model matematika dapat digunakan untuk memprediksi dampak perubahan iklim, seperti kenaikan permukaan air laut dan perubahan pola cuaca.
- Pemodelan ekonomi: Model matematika dapat digunakan untuk memprediksi pertumbuhan ekonomi, inflasi, dan pengangguran.
- Pemodelan aliran lalu lintas: Model matematika dapat digunakan untuk menganalisis aliran lalu lintas dan mengembangkan strategi untuk mengurangi kemacetan.
Proses Penelitian yang Melibatkan Model Matematika
Berikut adalah diagram alur yang menunjukkan proses penelitian yang melibatkan model matematika:
Diagram alur tersebut menunjukkan bahwa proses penelitian yang melibatkan model matematika dimulai dengan identifikasi masalah dan pengumpulan data. Setelah data dikumpulkan, model matematika dibuat dan divalidasi. Model matematika kemudian digunakan untuk membuat prediksi dan menyusun solusi. Akhirnya, hasil penelitian diinterpretasikan dan disimpulkan.
Tantangan dan Peluang Model Matematika
Model matematika telah menjadi alat penting dalam berbagai bidang, mulai dari sains dan teknik hingga ekonomi dan keuangan. Namun, pengembangan dan penerapan model matematika juga dihadapkan pada sejumlah tantangan dan peluang.
Tantangan dalam Pengembangan dan Penerapan Model Matematika
Tantangan utama dalam pengembangan dan penerapan model matematika adalah kompleksitas sistem nyata. Sistem nyata sering kali melibatkan banyak variabel, interaksi yang kompleks, dan ketidakpastian. Hal ini membuat sulit untuk membangun model yang akurat dan realistis.
- Kompleksitas Sistem Nyata: Model matematika idealnya merepresentasikan sistem nyata dengan akurat, tetapi realitas seringkali jauh lebih kompleks. Sistem melibatkan banyak variabel, interaksi yang rumit, dan ketidakpastian yang sulit dimodelkan secara sempurna.
- Keterbatasan Data: Model matematika membutuhkan data yang cukup dan berkualitas tinggi untuk pelatihan dan validasi. Data yang tidak lengkap, tidak akurat, atau bias dapat menyebabkan model yang tidak akurat dan tidak dapat diandalkan.
- Interpretasi dan Validasi: Setelah model dikembangkan, interpretasi dan validasi hasil sangat penting. Model matematika yang kompleks mungkin sulit dipahami dan diinterpretasikan, dan validasi membutuhkan data tambahan atau simulasi yang intensif.
Peluang dalam Pengembangan dan Penerapan Model Matematika
Meskipun ada tantangan, perkembangan teknologi dan metodologi baru membuka peluang untuk meningkatkan akurasi dan kegunaan model matematika.
- Kecerdasan Buatan (AI): AI, terutama pembelajaran mesin (ML), telah memberikan alat baru untuk membangun model yang lebih kompleks dan akurat. Algoritma ML dapat belajar dari data besar dan mengidentifikasi pola yang sulit ditangkap oleh metode tradisional.
- Komputasi Berkecepatan Tinggi: Peningkatan daya komputasi memungkinkan model matematika yang lebih kompleks dan rinci untuk dijalankan. Ini memungkinkan untuk mensimulasikan sistem yang lebih realistis dan mendapatkan hasil yang lebih akurat.
- Data Besar: Ketersediaan data besar membuka peluang untuk membangun model yang lebih kuat dan akurat. Data besar memungkinkan algoritma ML untuk belajar dari pola yang lebih kompleks dan menghasilkan prediksi yang lebih akurat.
Dampak Positif dan Negatif Penggunaan Model Matematika
| Dampak | Positif | Negatif |
|---|---|---|
| Akurasi dan Prediksi | Model matematika dapat meningkatkan akurasi prediksi dan pengambilan keputusan. | Model yang tidak akurat dapat menyebabkan keputusan yang salah dan kerugian. |
| Efisiensi dan Otomatisasi | Model matematika dapat mengotomatisasi tugas-tugas yang kompleks dan meningkatkan efisiensi. | Penggunaan model matematika dapat menyebabkan hilangnya pekerjaan manusia. |
| Pemahaman dan Pengetahuan | Model matematika dapat membantu memahami sistem yang kompleks dan menghasilkan pengetahuan baru. | Model matematika dapat digunakan untuk memanipulasi data dan menghasilkan informasi yang menyesatkan. |
Ringkasan Akhir
Memahami model matematika tidak hanya penting bagi para ilmuwan dan profesional, tetapi juga bagi kita semua. Dengan kemampuan untuk menganalisis data dan membuat prediksi yang akurat, kita dapat menjadi warga negara yang lebih cerdas, konsumen yang lebih bijak, dan pengambil keputusan yang lebih efektif.






