Contoh Soal Percepatan Sesaat: Mengukur Perubahan Kecepatan Seketika

Contoh soal percepatan sesaat – Pernahkah kamu memperhatikan bagaimana mobil yang melaju cepat bisa berhenti dengan cepat saat lampu merah menyala? Atau bagaimana bola yang dilempar ke atas melambat saat mencapai titik tertinggi sebelum akhirnya jatuh kembali? Di balik gerakan-gerakan tersebut, terdapat konsep fisika yang menarik bernama percepatan sesaat. Percepatan sesaat mengukur seberapa cepat kecepatan suatu benda berubah pada suatu titik waktu tertentu. Bayangkan seperti zoom-in ke kecepatan benda pada momen yang sangat singkat!

Dalam artikel ini, kita akan menjelajahi konsep percepatan sesaat dengan contoh soal yang menarik. Mulai dari memahami definisi dan rumus, hingga melihat penerapannya dalam kehidupan sehari-hari, kita akan mengungkap bagaimana percepatan sesaat berperan penting dalam menjelaskan gerakan benda di sekitar kita.

Pengertian Percepatan Sesaat

Dalam dunia fisika, kita seringkali mempelajari tentang perubahan kecepatan suatu benda. Percepatan sesaat merupakan konsep penting yang menggambarkan bagaimana kecepatan suatu benda berubah pada suatu titik waktu tertentu. Konsep ini berbeda dengan percepatan rata-rata yang mengukur perubahan kecepatan selama selang waktu tertentu.

Percepatan Sesaat

Percepatan sesaat didefinisikan sebagai laju perubahan kecepatan pada suatu titik waktu tertentu. Dengan kata lain, percepatan sesaat adalah turunan pertama dari kecepatan terhadap waktu.

Percepatan sesaat dapat dirumuskan sebagai:

a = lim Δt→0 Δv/Δt

di mana:

a adalah percepatan sesaat

Δv adalah perubahan kecepatan

Δt adalah perubahan waktu

Rumus ini menunjukkan bahwa percepatan sesaat dihitung dengan membagi perubahan kecepatan dengan perubahan waktu yang sangat kecil, mendekati nol. Hal ini berarti bahwa kita melihat bagaimana kecepatan berubah pada titik waktu yang sangat spesifik.

Perbandingan dengan Percepatan Rata-rata

Percepatan rata-rata mengukur perubahan kecepatan total selama selang waktu tertentu, sedangkan percepatan sesaat mengukur perubahan kecepatan pada titik waktu tertentu. Perbedaan utama terletak pada interval waktu yang dipertimbangkan. Percepatan rata-rata menggunakan selang waktu yang lebih besar, sedangkan percepatan sesaat menggunakan selang waktu yang sangat kecil.

• Percepatan rata-rata adalah perubahan kecepatan total dibagi dengan selang waktu total.
• Percepatan sesaat adalah perubahan kecepatan pada titik waktu tertentu.

Contoh Ilustrasi

Bayangkan sebuah mobil yang melaju di jalan raya. Kita dapat mengukur percepatan rata-rata mobil tersebut dengan membagi perubahan kecepatan total dengan selang waktu total perjalanan. Namun, jika kita ingin mengetahui bagaimana kecepatan mobil berubah pada saat tertentu, misalnya saat mobil melewati tikungan tajam, kita perlu menggunakan konsep percepatan sesaat. Percepatan sesaat akan menunjukkan bagaimana kecepatan mobil berubah pada saat tepat mobil melewati tikungan tersebut.

Rumus Percepatan Sesaat

Percepatan sesaat adalah perubahan kecepatan suatu benda dalam waktu yang sangat singkat. Kita dapat menghitung percepatan sesaat dengan menggunakan konsep turunan dalam kalkulus.

Rumus Percepatan Sesaat

Rumus percepatan sesaat digunakan untuk menghitung percepatan suatu benda pada suatu titik waktu tertentu. Percepatan sesaat didefinisikan sebagai turunan pertama dari kecepatan terhadap waktu.

$$a(t) = \fracdv(t)dt$$

Keterangan:

* $a(t)$ adalah percepatan sesaat pada waktu $t$
* $v(t)$ adalah kecepatan pada waktu $t$
* $\fracdv(t)dt$ adalah turunan pertama dari kecepatan terhadap waktu

Variabel dalam Rumus Percepatan Sesaat

Berikut adalah tabel yang berisi variabel, satuan, dan definisi untuk setiap variabel dalam rumus percepatan sesaat:

Variabel	Satuan	Definisi
$a(t)$	m/s2	Percepatan sesaat pada waktu $t$
$v(t)$	m/s	Kecepatan pada waktu $t$
$t$	s	Waktu

Contoh Perhitungan Percepatan Sesaat

Misalnya, kita ingin menghitung percepatan sesaat sebuah mobil pada waktu $t = 2$ detik, jika kecepatan mobil tersebut dinyatakan dengan persamaan $v(t) = 3t^2 + 2t$.

Pertama, kita cari turunan pertama dari persamaan kecepatan:

$$\fracdv(t)dt = 6t + 2$$

Kemudian, kita substitusikan nilai $t = 2$ detik ke dalam persamaan turunan:

$$a(2) = 6(2) + 2 = 14 \text m/s^2$$

Jadi, percepatan sesaat mobil tersebut pada waktu $t = 2$ detik adalah $14 \text m/s^2$.

Menentukan Percepatan Sesaat dari Grafik Kecepatan-Waktu

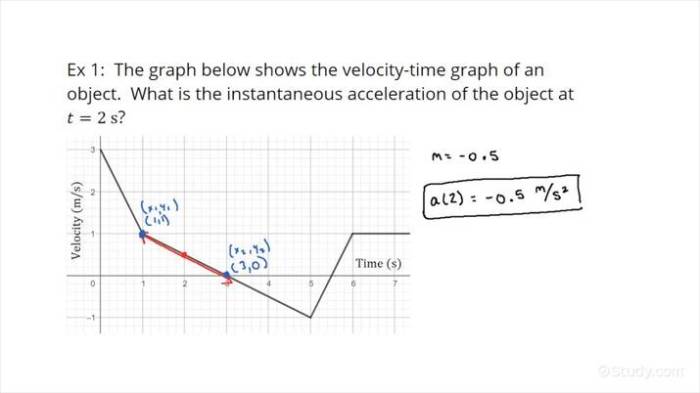
Percepatan sesaat menggambarkan seberapa cepat kecepatan suatu objek berubah pada suatu titik waktu tertentu. Dalam konteks grafik kecepatan-waktu, percepatan sesaat dapat ditentukan dengan mencari kemiringan garis singgung pada titik waktu yang dimaksud.

Menentukan Percepatan Sesaat dari Grafik Kecepatan-Waktu

Untuk menentukan percepatan sesaat pada titik tertentu dalam grafik kecepatan-waktu, kita perlu mengidentifikasi garis singgung yang melewati titik tersebut. Garis singgung adalah garis lurus yang menyentuh kurva pada titik tersebut tanpa memotongnya. Kemiringan garis singgung ini mewakili percepatan sesaat pada titik waktu yang bersangkutan.

Contoh Grafik Kecepatan-Waktu dan Cara Menentukan Percepatan Sesaat

Misalnya, perhatikan grafik kecepatan-waktu berikut yang menggambarkan gerakan suatu mobil:

Gambarlah grafik kecepatan-waktu dengan sumbu x mewakili waktu (t) dan sumbu y mewakili kecepatan (v). Kurva pada grafik menunjukkan perubahan kecepatan mobil seiring waktu. Pilih titik tertentu pada kurva, misalnya pada waktu t1. Gambarlah garis singgung yang melewati titik tersebut. Garis singgung harus menyentuh kurva pada titik t1 tanpa memotongnya. Hitung kemiringan garis singgung tersebut. Kemiringan garis singgung ini mewakili percepatan sesaat mobil pada waktu t1.

Kemiringan garis singgung dapat dihitung dengan menggunakan rumus:

Kemiringan = (Perubahan Kecepatan) / (Perubahan Waktu)

Contoh soal percepatan sesaat, misalnya, menghitung perubahan kecepatan objek dalam rentang waktu tertentu. Konsep ini mirip dengan marginal cost dalam ekonomi, yang mengukur perubahan biaya produksi saat menghasilkan satu unit tambahan. Contoh soal marginal cost biasanya melibatkan analisis perubahan total biaya produksi dan kuantitas output.

Begitu juga dengan contoh soal percepatan sesaat, kita bisa mempelajari perubahan kecepatan dan waktu untuk memahami gerakan objek dengan lebih detail.

Dengan demikian, percepatan sesaat mobil pada waktu t1 dapat ditentukan dengan menghitung kemiringan garis singgung pada titik t1.

Penerapan Percepatan Sesaat dalam Kehidupan Sehari-hari

Konsep percepatan sesaat mungkin terdengar rumit, tapi sebenarnya ia hadir dalam berbagai aspek kehidupan kita. Percepatan sesaat menggambarkan perubahan kecepatan suatu benda dalam waktu yang sangat singkat, dan konsep ini memiliki peran penting dalam berbagai situasi, mulai dari berkendara hingga olahraga.

Percepatan Sesaat dalam Berkendara

Ketika kamu mengemudi mobil, percepatan sesaat memainkan peran penting dalam mengendalikan kendaraan. Saat kamu menginjak pedal gas, kamu meningkatkan percepatan mobil, dan ketika kamu menginjak rem, kamu mengurangi percepatan. Percepatan sesaat memungkinkan kamu untuk mempercepat atau memperlambat mobil dengan halus dan terkontrol, memastikan perjalanan yang aman dan nyaman.

Percepatan Sesaat dalam Olahraga

• Pelari: Pelari yang ingin mencapai kecepatan maksimum membutuhkan percepatan sesaat yang tinggi di awal lari. Mereka menggunakan kekuatan otot untuk mempercepat tubuh mereka dengan cepat, memungkinkan mereka untuk mencapai kecepatan lari yang lebih tinggi.
• Atlet Lompat: Atlet lompat seperti atlet lompat tinggi dan lompat jauh memanfaatkan percepatan sesaat untuk menghasilkan gaya yang kuat. Mereka mempercepat tubuh mereka sebelum melompat, menghasilkan dorongan yang kuat yang membantu mereka mencapai ketinggian atau jarak lompatan yang lebih jauh.

Percepatan Sesaat dalam Penerbangan

Percepatan sesaat juga memainkan peran penting dalam penerbangan. Pesawat terbang membutuhkan percepatan sesaat yang tinggi untuk lepas landas. Mesin pesawat menghasilkan gaya dorong yang kuat, mempercepat pesawat hingga mencapai kecepatan yang cukup untuk mengangkatnya dari tanah.

Percepatan Sesaat dalam Roller Coaster

Percepatan sesaat adalah kunci dalam menciptakan sensasi menegangkan dalam wahana roller coaster. Roller coaster dirancang untuk memberikan percepatan sesaat yang tinggi dan tiba-tiba, menghasilkan pengalaman yang mengasyikkan dan menegangkan bagi para pengunjung.

Contoh Soal Percepatan Sesaat dan Penyelesaiannya

Percepatan sesaat adalah laju perubahan kecepatan suatu benda pada suatu titik waktu tertentu. Percepatan sesaat menunjukkan seberapa cepat kecepatan suatu benda berubah pada saat itu juga.

Untuk memahami konsep percepatan sesaat lebih dalam, mari kita bahas beberapa contoh soal dan penyelesaiannya.

Contoh Soal Percepatan Sesaat

Berikut adalah tiga contoh soal tentang percepatan sesaat dengan tingkat kesulitan yang berbeda:

• Soal 1: Sebuah mobil bergerak dengan kecepatan awal 10 m/s dan mengalami percepatan konstan sebesar 2 m/s². Tentukan percepatan sesaat mobil tersebut setelah 5 detik.
• Soal 2: Sebuah bola dilempar vertikal ke atas dengan kecepatan awal 20 m/s. Tentukan percepatan sesaat bola tersebut ketika mencapai titik tertinggi.
• Soal 3: Sebuah partikel bergerak dengan persamaan gerak s(t) = t³ – 2t² + 5t. Tentukan percepatan sesaat partikel tersebut ketika t = 2 detik.

Penyelesaian Soal Percepatan Sesaat

Berikut adalah langkah-langkah penyelesaian untuk setiap soal:

Soal	Rumus yang Digunakan	Jawaban
Soal 1: Sebuah mobil bergerak dengan kecepatan awal 10 m/s dan mengalami percepatan konstan sebesar 2 m/s². Tentukan percepatan sesaat mobil tersebut setelah 5 detik.	a = a	Percepatan sesaat mobil tersebut adalah 2 m/s². Karena percepatan konstan, percepatan sesaatnya sama dengan percepatan konstannya.
Soal 2: Sebuah bola dilempar vertikal ke atas dengan kecepatan awal 20 m/s. Tentukan percepatan sesaat bola tersebut ketika mencapai titik tertinggi.	a = -g (g = percepatan gravitasi)	Percepatan sesaat bola tersebut adalah -9,8 m/s². Ketika bola mencapai titik tertinggi, kecepatannya menjadi nol, tetapi percepatannya tetap sama dengan percepatan gravitasi, yaitu -9,8 m/s².
Soal 3: Sebuah partikel bergerak dengan persamaan gerak s(t) = t³ – 2t² + 5t. Tentukan percepatan sesaat partikel tersebut ketika t = 2 detik.	a = d²s/dt²	Percepatan sesaat partikel tersebut adalah 10 m/s². Percepatan sesaat diperoleh dengan menghitung turunan kedua dari persamaan gerak terhadap waktu. Dalam kasus ini, a(t) = 6t – 4, sehingga a(2) = 10 m/s².

Hubungan Percepatan Sesaat dengan Gaya

Percepatan sesaat adalah perubahan kecepatan suatu benda dalam rentang waktu yang sangat singkat. Percepatan sesaat ini erat kaitannya dengan gaya yang bekerja pada benda tersebut. Gaya merupakan faktor yang dapat menyebabkan benda bergerak, berhenti, atau mengubah arah geraknya. Dalam artikel ini, kita akan menjelajahi hubungan erat antara percepatan sesaat dan gaya yang bekerja pada suatu benda.

Hukum Newton Kedua tentang Gerak

Hukum Newton kedua tentang gerak merupakan dasar pemahaman kita tentang hubungan antara gaya, massa, dan percepatan. Hukum ini menyatakan bahwa percepatan suatu benda sebanding dengan gaya total yang bekerja padanya dan berbanding terbalik dengan massanya. Dengan kata lain, semakin besar gaya yang bekerja pada benda, semakin besar pula percepatannya. Sebaliknya, semakin besar massa benda, semakin kecil percepatannya.

Secara matematis, hukum Newton kedua dapat dirumuskan sebagai berikut:

F = ma

di mana:

• F adalah gaya total yang bekerja pada benda
• m adalah massa benda
• a adalah percepatan benda

Persamaan ini menunjukkan bahwa percepatan sesaat suatu benda secara langsung dipengaruhi oleh gaya yang bekerja padanya. Semakin besar gaya yang bekerja, semakin besar percepatan sesaatnya. Sebaliknya, semakin kecil gaya yang bekerja, semakin kecil percepatan sesaatnya.

Contoh Gaya yang Mempengaruhi Percepatan Sesaat

Berikut adalah beberapa contoh bagaimana gaya memengaruhi percepatan sesaat suatu benda:

• Sebuah mobil yang sedang melaju: Ketika pengemudi menginjak pedal gas, gaya yang dihasilkan oleh mesin mobil akan menyebabkan mobil tersebut mengalami percepatan. Semakin kuat pengemudi menginjak pedal gas, semakin besar gaya yang dihasilkan, dan semakin besar percepatan sesaat mobil tersebut.
• Sebuah bola yang dilempar ke atas: Ketika bola dilempar ke atas, gaya gravitasi bumi bekerja pada bola tersebut, menyebabkan bola mengalami percepatan ke bawah. Semakin besar massa bola, semakin besar gaya gravitasi yang bekerja padanya, dan semakin besar percepatan sesaat ke bawah yang dialami bola tersebut.
• Sebuah benda yang didorong di atas permukaan yang kasar: Ketika benda didorong di atas permukaan yang kasar, gaya gesekan antara benda dan permukaan tersebut akan bekerja pada benda, menyebabkan benda mengalami percepatan yang lebih lambat. Semakin besar gaya gesekan, semakin kecil percepatan sesaat benda tersebut.

Percepatan Sesaat dalam Gerak Melingkar

Gerak melingkar, seperti saat roda berputar atau benda bergerak dalam lintasan melingkar, memiliki karakteristik unik dalam hal percepatan. Percepatan sesaat dalam gerak melingkar mengacu pada perubahan kecepatan benda pada titik waktu tertentu. Kecepatan dalam gerak melingkar merupakan besaran vektor, sehingga perubahan kecepatan dapat terjadi karena perubahan besarnya kecepatan atau arahnya, atau keduanya. Percepatan sesaat dalam gerak melingkar, berbeda dengan percepatan dalam gerak lurus, karena melibatkan komponen percepatan sentripetal yang selalu mengarah ke pusat lingkaran.

Konsep Percepatan Sesaat dalam Gerak Melingkar

Percepatan sesaat dalam gerak melingkar adalah perubahan kecepatan sesaat suatu benda yang bergerak melingkar pada suatu titik waktu tertentu. Kecepatan dalam gerak melingkar merupakan besaran vektor, yang berarti memiliki besar dan arah. Percepatan sesaat dalam gerak melingkar dapat terjadi karena perubahan besarnya kecepatan, perubahan arah kecepatan, atau keduanya.

Dalam gerak melingkar, kecepatan benda selalu berubah arah, meskipun besarnya kecepatan tetap. Hal ini karena benda selalu bergerak dalam lintasan melingkar, yang berarti arah kecepatannya selalu berubah. Perubahan arah kecepatan ini menyebabkan percepatan, yang disebut percepatan sentripetal. Percepatan sentripetal selalu mengarah ke pusat lingkaran, dan bertanggung jawab untuk menjaga benda agar tetap bergerak dalam lintasan melingkar.

Perbandingan Percepatan Sesaat dalam Gerak Melingkar dan Gerak Lurus

Percepatan sesaat dalam gerak melingkar berbeda dengan percepatan sesaat dalam gerak lurus. Dalam gerak lurus, percepatan hanya terjadi karena perubahan besarnya kecepatan. Namun, dalam gerak melingkar, percepatan dapat terjadi karena perubahan besarnya kecepatan, perubahan arah kecepatan, atau keduanya.

• Dalam gerak lurus, percepatan selalu sejajar dengan arah kecepatan.
• Dalam gerak melingkar, percepatan sentripetal selalu tegak lurus dengan arah kecepatan, dan mengarah ke pusat lingkaran.

Contoh Ilustrasi Gerak Melingkar

Bayangkan sebuah mobil yang bergerak dengan kecepatan konstan di sekitar lintasan melingkar. Meskipun kecepatan mobil tetap, arah kecepatannya selalu berubah. Percepatan sesaat mobil pada titik tertentu selalu mengarah ke pusat lingkaran.

Arah percepatan sesaat pada titik tertentu dapat diilustrasikan dengan vektor. Vektor percepatan sesaat akan mengarah ke pusat lingkaran, dan besarnya akan sebanding dengan besarnya perubahan kecepatan sesaat.

Percepatan Sesaat dalam Gerak Parabola

Gerak parabola merupakan gerak benda yang melengkung dan dipengaruhi oleh gaya gravitasi bumi. Percepatan sesaat dalam gerak parabola merupakan besaran yang menunjukkan laju perubahan kecepatan benda pada suatu titik waktu tertentu selama pergerakannya. Percepatan sesaat ini memiliki arah dan besar yang berubah-ubah selama gerakan parabola.

Konsep Percepatan Sesaat dalam Gerak Parabola

Percepatan sesaat dalam gerak parabola selalu berarah ke bawah dan memiliki nilai yang sama dengan percepatan gravitasi bumi (g). Meskipun kecepatan benda berubah-ubah selama gerakan parabola, baik dalam arah horizontal maupun vertikal, percepatan sesaat tetap konstan dan berarah ke bawah.

Perubahan Percepatan Sesaat Selama Gerak Parabola

Percepatan sesaat dalam gerak parabola tetap konstan selama seluruh gerakan. Ini berarti bahwa kecepatan benda berubah secara konstan, baik dalam arah horizontal maupun vertikal, karena pengaruh percepatan gravitasi bumi.

Ilustrasi Gerak Parabola dengan Penanda Titik Tertentu

Perhatikan ilustrasi gerak parabola berikut:

Sebuah bola dilempar dengan kecepatan awal v0 pada sudut θ terhadap horizontal. Bola tersebut akan bergerak membentuk lintasan parabola. Titik A adalah titik awal peluncuran bola, titik B adalah titik tertinggi yang dicapai bola, dan titik C adalah titik di mana bola mencapai tanah.

• Pada titik A, kecepatan awal bola memiliki komponen horizontal (v0x) dan vertikal (v0y). Percepatan sesaat pada titik A berarah ke bawah dan memiliki nilai g.
• Pada titik B, kecepatan vertikal bola menjadi nol, sedangkan kecepatan horizontal tetap sama dengan v0x. Percepatan sesaat pada titik B tetap berarah ke bawah dan memiliki nilai g.
• Pada titik C, kecepatan vertikal bola sama dengan -v0y, sedangkan kecepatan horizontal tetap sama dengan v0x. Percepatan sesaat pada titik C tetap berarah ke bawah dan memiliki nilai g.

Meskipun kecepatan bola berubah-ubah selama gerakan parabola, percepatan sesaat tetap konstan dan berarah ke bawah, yaitu sebesar percepatan gravitasi bumi (g).

Percepatan Sesaat dalam Gerak Rotasi

Gerak rotasi, seperti putaran roda atau perputaran bumi, memiliki karakteristik yang unik. Dalam gerak rotasi, setiap titik pada objek bergerak dalam lingkaran, dan kecepatannya bisa berubah seiring waktu. Percepatan sesaat dalam gerak rotasi mengacu pada perubahan kecepatan sudut suatu titik pada objek yang berputar pada suatu waktu tertentu. Konsep ini penting untuk memahami bagaimana objek berputar dan bagaimana gaya yang bekerja pada objek tersebut.

Konsep Percepatan Sesaat dalam Gerak Rotasi, Contoh soal percepatan sesaat

Percepatan sesaat dalam gerak rotasi didefinisikan sebagai laju perubahan kecepatan sudut terhadap waktu. Kecepatan sudut adalah ukuran seberapa cepat suatu objek berputar, dan diukur dalam radian per detik (rad/s). Percepatan sudut, di sisi lain, diukur dalam radian per detik kuadrat (rad/s²).

Rumus untuk menghitung percepatan sesaat dalam gerak rotasi adalah:

α = dω/dt

Dimana:

• α adalah percepatan sudut
• ω adalah kecepatan sudut
• t adalah waktu

Perbandingan dengan Percepatan Sesaat dalam Gerak Linier

Percepatan sesaat dalam gerak linier adalah perubahan kecepatan linear terhadap waktu. Kecepatan linear adalah ukuran seberapa cepat suatu objek bergerak dalam garis lurus, dan diukur dalam meter per detik (m/s). Percepatan linear, di sisi lain, diukur dalam meter per detik kuadrat (m/s²).

Perbedaan utama antara percepatan sesaat dalam gerak rotasi dan gerak linier adalah bahwa percepatan sesaat dalam gerak rotasi mengukur perubahan kecepatan sudut, sedangkan percepatan sesaat dalam gerak linier mengukur perubahan kecepatan linear. Percepatan sesaat dalam gerak rotasi juga dapat dikaitkan dengan percepatan sentripetal, yang merupakan percepatan yang mengarahkan objek ke pusat lingkaran yang dilalui.

Contoh Ilustrasi Gerak Rotasi

Bayangkan sebuah roda sepeda yang berputar. Setiap titik pada roda bergerak dalam lingkaran, dan kecepatannya bisa berubah seiring waktu. Misalnya, jika roda sepeda dipercepat, kecepatan sudutnya akan meningkat, dan percepatan sudutnya akan positif. Jika roda sepeda diperlambat, kecepatan sudutnya akan berkurang, dan percepatan sudutnya akan negatif.

Arah percepatan sesaat pada titik tertentu pada roda sepeda akan selalu menuju ke pusat lingkaran yang dilalui oleh titik tersebut. Ini karena percepatan sesaat merupakan percepatan sentripetal yang diperlukan untuk menjaga titik tersebut bergerak dalam lingkaran.

Percepatan Sesaat dalam Fisika Modern

Percepatan sesaat, yang mengukur perubahan kecepatan suatu objek pada titik waktu tertentu, memegang peran penting dalam fisika modern. Konsep ini memungkinkan kita untuk memahami perilaku objek dalam berbagai skenario, dari gerakan planet di ruang angkasa hingga partikel subatomik di dunia kuantum.

Penerapan Percepatan Sesaat dalam Fisika Modern

Percepatan sesaat diterapkan dalam berbagai aspek fisika modern, terutama dalam memahami perilaku objek dalam sistem dinamis yang rumit.

• Dalam mekanika klasik, percepatan sesaat digunakan untuk menganalisis gerakan benda yang mengalami gaya yang berubah-ubah, seperti gerakan benda yang jatuh bebas atau gerakan mobil yang sedang mengerem.
• Dalam fisika modern, konsep percepatan sesaat diterapkan untuk menganalisis gerakan partikel subatomik dalam teori relativitas dan mekanika kuantum.

Percepatan Sesaat dalam Teori Relativitas

Teori relativitas Einstein, yang mengkaji gerakan benda pada kecepatan tinggi mendekati kecepatan cahaya, menggunakan konsep percepatan sesaat untuk memahami bagaimana kecepatan dan waktu dipengaruhi oleh gravitasi.

• Dalam teori relativitas khusus, percepatan sesaat digunakan untuk menghitung perubahan kecepatan dan waktu relatif terhadap kerangka acuan yang berbeda.
• Dalam teori relativitas umum, percepatan sesaat digunakan untuk menggambarkan bagaimana gravitasi memengaruhi gerakan benda dan bagaimana waktu terdistorsi di sekitar benda bermassa besar, seperti bintang dan lubang hitam.

Percepatan Sesaat dalam Mekanika Kuantum

Mekanika kuantum, yang mempelajari perilaku partikel pada skala atom dan subatomik, menggunakan konsep percepatan sesaat untuk menggambarkan gerakan partikel yang tidak dapat diprediksi secara pasti.

• Dalam mekanika kuantum, percepatan sesaat didefinisikan sebagai turunan waktu dari momentum partikel.
• Konsep ini digunakan untuk menjelaskan fenomena seperti efek tunneling, di mana partikel dapat melewati penghalang yang seharusnya tidak dapat ditembus, dan efek ketidakpastian Heisenberg, yang menyatakan bahwa kita tidak dapat mengetahui secara pasti posisi dan momentum suatu partikel secara bersamaan.

Perkembangan Konsep Percepatan Sesaat dalam Fisika Modern

Konsep percepatan sesaat telah berkembang seiring dengan kemajuan fisika modern.

• Awalnya, konsep percepatan sesaat dikembangkan dalam konteks mekanika klasik untuk menggambarkan gerakan benda makroskopis.
• Dengan munculnya teori relativitas dan mekanika kuantum, konsep percepatan sesaat telah diperluas untuk menggambarkan perilaku partikel subatomik dan objek pada kecepatan tinggi.
• Perkembangan teori-teori ini telah membuka pemahaman yang lebih mendalam tentang alam semesta dan memungkinkan kita untuk mempelajari fenomena yang sebelumnya tidak dapat dijelaskan.

Ulasan Penutup: Contoh Soal Percepatan Sesaat

Memahami percepatan sesaat membuka pintu untuk memahami berbagai fenomena fisika yang terjadi di sekitar kita. Dari gerakan mobil di jalan hingga jatuhnya buah dari pohon, konsep ini membantu kita memahami bagaimana kecepatan benda berubah seiring waktu. Dengan memahami percepatan sesaat, kita dapat memprediksi dan mengendalikan gerakan benda dengan lebih baik, yang sangat penting dalam berbagai bidang seperti ilmu pengetahuan, teknologi, dan olahraga.