Pernahkah kamu bertanya-tanya bagaimana cara menyelesaikan pertidaksamaan yang melibatkan nilai mutlak? Contoh Soal Pertidaksamaan Nilai Mutlak dan Penyelesaiannya akan memandu kamu memahami konsep dasar, langkah-langkah penyelesaian, dan berbagai aplikasi pertidaksamaan nilai mutlak dalam berbagai bidang.
Pertidaksamaan nilai mutlak adalah konsep penting dalam matematika yang memungkinkan kita untuk menganalisis dan menyelesaikan masalah yang melibatkan jarak, toleransi, dan batasan. Dalam panduan ini, kita akan menjelajahi pengertian nilai mutlak, konsep pertidaksamaan nilai mutlak, metode penyelesaian, dan aplikasi dalam kehidupan nyata.
Pengertian Nilai Mutlak
Nilai mutlak merupakan konsep penting dalam matematika yang merepresentasikan jarak suatu bilangan dari nol pada garis bilangan, tanpa mempertimbangkan arahnya. Nilai mutlak selalu bernilai non-negatif.
Contoh Nilai Mutlak
Nilai mutlak dari suatu bilangan dapat dihitung dengan menggunakan simbol “| |”. Misalnya:
- |5| = 5, karena jarak 5 dari 0 pada garis bilangan adalah 5.
- |-3| = 3, karena jarak -3 dari 0 pada garis bilangan adalah 3.
- |0| = 0, karena jarak 0 dari 0 pada garis bilangan adalah 0.
- |2.5| = 2.5, karena jarak 2.5 dari 0 pada garis bilangan adalah 2.5.
- |-1/2| = 1/2, karena jarak -1/2 dari 0 pada garis bilangan adalah 1/2.
Interpretasi Geometri Nilai Mutlak
Nilai mutlak dapat diinterpretasikan secara geometri sebagai jarak suatu titik dari titik asal (0) pada garis bilangan.
| Bilangan | Nilai Mutlak | Interpretasi Geometri |
|---|---|---|
| 5 | |5| = 5 | Jarak titik 5 dari titik asal (0) adalah 5 satuan. |
| -3 | |-3| = 3 | Jarak titik -3 dari titik asal (0) adalah 3 satuan. |
| 0 | |0| = 0 | Jarak titik 0 dari titik asal (0) adalah 0 satuan. |
Pertidaksamaan Nilai Mutlak
Pertidaksamaan nilai mutlak merupakan bentuk pertidaksamaan yang melibatkan nilai mutlak suatu ekspresi aljabar. Konsep ini penting dalam berbagai bidang seperti matematika, fisika, dan teknik. Dalam artikel ini, kita akan menjelajahi konsep pertidaksamaan nilai mutlak, membahas berbagai bentuknya, dan merinci langkah-langkah umum untuk menyelesaikannya.
Konsep Pertidaksamaan Nilai Mutlak
Nilai mutlak suatu bilangan adalah jarak bilangan tersebut dari nol pada garis bilangan. Secara formal, nilai mutlak dari suatu bilangan x, dilambangkan dengan |x|, didefinisikan sebagai:
|x| = x jika x ≥ 0
|x| = -x jika x < 0
Misalnya, |3| = 3 dan |-3| = 3. Dengan memahami konsep nilai mutlak, kita dapat memahami pertidaksamaan nilai mutlak.
Bentuk Pertidaksamaan Nilai Mutlak
Pertidaksamaan nilai mutlak memiliki beberapa bentuk umum:
- |x| < a
- |x| > a
- |x – a| < b
- |x – a| > b
Di mana a dan b adalah bilangan real positif.
Langkah-Langkah Umum untuk Menyelesaikan Pertidaksamaan Nilai Mutlak
Berikut adalah langkah-langkah umum untuk menyelesaikan pertidaksamaan nilai mutlak:
- Identifikasi bentuk pertidaksamaan. Tentukan apakah pertidaksamaan tersebut berbentuk |x| a, |x – a| b.
- Tentukan nilai mutlak. Untuk bentuk |x| a, nilai mutlak sudah diketahui. Untuk bentuk |x – a| b, tentukan nilai mutlak dari ekspresi di dalam tanda mutlak.
- Selesaikan pertidaksamaan. Bagi pertidaksamaan menjadi dua kasus, satu untuk x ≥ 0 dan satu untuk x < 0. Selesaikan pertidaksamaan untuk setiap kasus.
- Gabungkan solusi. Gabungkan solusi dari kedua kasus untuk mendapatkan solusi lengkap pertidaksamaan.
Metode Penyelesaian Pertidaksamaan Nilai Mutlak
Pertidaksamaan nilai mutlak merupakan pertidaksamaan yang memuat ekspresi nilai mutlak. Dalam menyelesaikan pertidaksamaan nilai mutlak, terdapat beberapa metode yang dapat digunakan, seperti metode grafik, sifat-sifat nilai mutlak, dan metode aljabar. Metode yang digunakan dapat disesuaikan dengan bentuk pertidaksamaan nilai mutlak yang diberikan.
Metode Grafik
Metode grafik dapat digunakan untuk menyelesaikan pertidaksamaan nilai mutlak dengan memanfaatkan sifat-sifat nilai mutlak dan representasi grafik fungsi nilai mutlak. Berikut langkah-langkahnya:
- Tentukan fungsi nilai mutlak yang terkait dengan pertidaksamaan.
- Gambar grafik fungsi nilai mutlak tersebut pada bidang Cartesius.
- Tentukan daerah yang memenuhi pertidaksamaan berdasarkan tanda pertidaksamaan dan posisi grafik fungsi nilai mutlak.
- Tuliskan solusi pertidaksamaan dalam bentuk interval.
Metode Sifat-Sifat Nilai Mutlak
Metode ini memanfaatkan sifat-sifat nilai mutlak untuk mengubah pertidaksamaan nilai mutlak menjadi bentuk pertidaksamaan biasa yang lebih mudah diselesaikan. Beberapa sifat nilai mutlak yang dapat digunakan, antara lain:
- Jika |x| < a, maka -a < x < a.
- Jika |x| > a, maka x a.
- Jika |x| = a, maka x = a atau x = -a.
Metode Aljabar
Metode aljabar merupakan metode yang paling umum digunakan untuk menyelesaikan pertidaksamaan nilai mutlak. Metode ini melibatkan manipulasi aljabar untuk memisahkan ekspresi nilai mutlak dan menyelesaikan pertidaksamaan biasa. Berikut langkah-langkahnya:
- Tentukan ekspresi nilai mutlak yang ada dalam pertidaksamaan.
- Pisahkan pertidaksamaan menjadi dua kasus, yaitu ketika ekspresi di dalam nilai mutlak bernilai positif dan negatif.
- Selesaikan kedua kasus tersebut secara terpisah dengan manipulasi aljabar.
- Gabungkan solusi dari kedua kasus tersebut untuk mendapatkan solusi keseluruhan.
Berikut contoh soal pertidaksamaan nilai mutlak dengan metode penyelesaian aljabar:
|2x – 1| < 5
Langkah-langkah penyelesaian:
- Pisahkan pertidaksamaan menjadi dua kasus:
- Kasus 1: 2x – 1 ≥ 0, maka |2x – 1| = 2x – 1.
- Kasus 2: 2x – 1 < 0, maka |2x – 1| = -(2x – 1) = -2x + 1.
- Selesaikan kedua kasus tersebut:
- Kasus 1: 2x – 1 < 5, maka 2x < 6, sehingga x < 3.
- Kasus 2: -2x + 1 < 5, maka -2x -2.
- Gabungkan solusi dari kedua kasus tersebut:
- Solusi keseluruhan adalah -2 < x < 3.
-
Soal 1: Tentukan penyelesaian dari pertidaksamaan |x – 2| < 5.
Solusi:
Pertidaksamaan |x – 2| < 5 berarti jarak antara x dan 2 kurang dari 5. Ini dapat diilustrasikan dengan garis bilangan.
Dari garis bilangan, kita dapat melihat bahwa penyelesaiannya adalah -3 < x < 7.
-
Soal 2: Tentukan penyelesaian dari pertidaksamaan |2x + 1| ≥ 3.
Solusi:
Pertidaksamaan |2x + 1| ≥ 3 berarti jarak antara 2x + 1 dan 0 lebih besar dari atau sama dengan 3. Ini dapat diilustrasikan dengan garis bilangan.
Contoh soal pertidaksamaan nilai mutlak dan penyelesaiannya memang menantang, tapi bisa jadi lebih mudah dengan memahami konsep dasar. Nah, mirip seperti pertidaksamaan, konsep energi kimia juga butuh pemahaman mendalam. Ingin belajar lebih lanjut tentang contoh soal energi kimia? Kamu bisa kunjungi contoh soal energi kimia untuk mendapatkan pemahaman yang lebih baik.
Kembali ke topik pertidaksamaan nilai mutlak, kunci utamanya adalah memahami bagaimana nilai mutlak mempengaruhi penyelesaian persamaan atau pertidaksamaan. Dengan latihan dan pemahaman yang baik, kamu pasti bisa menguasai keduanya!
Dari garis bilangan, kita dapat melihat bahwa penyelesaiannya adalah x ≤ -2 atau x ≥ 1.
-
Soal 3: Tentukan penyelesaian dari pertidaksamaan |x – 3| + |x + 2| < 5.
Solusi:
Untuk menyelesaikan pertidaksamaan ini, kita perlu mempertimbangkan tiga kasus:
- x ≤ -2: Dalam kasus ini, x – 3 < 0 dan x + 2 < 0, sehingga pertidaksamaan menjadi -(x – 3) – (x + 2) -3. Karena x ≤ -2, maka solusi untuk kasus ini adalah -3 < x ≤ -2.
- -2 ≤ x ≤ 3: Dalam kasus ini, x – 3 < 0 dan x + 2 ≥ 0, sehingga pertidaksamaan menjadi -(x – 3) + (x + 2) < 5, yang menghasilkan 5 < 5. Karena tidak ada nilai x yang memenuhi, maka tidak ada solusi untuk kasus ini.
- x ≥ 3: Dalam kasus ini, x – 3 ≥ 0 dan x + 2 ≥ 0, sehingga pertidaksamaan menjadi (x – 3) + (x + 2) < 5, yang menghasilkan x < 3. Karena x ≥ 3, maka tidak ada solusi untuk kasus ini.
Jadi, penyelesaian dari pertidaksamaan ini adalah -3 < x ≤ -2.
-
Soal 4: Tentukan penyelesaian dari pertidaksamaan |x² – 4| ≤ 5.
Solusi:
Pertidaksamaan |x² – 4| ≤ 5 berarti jarak antara x² – 4 dan 0 kurang dari atau sama dengan 5. Ini dapat diilustrasikan dengan garis bilangan.
Dari garis bilangan, kita dapat melihat bahwa penyelesaiannya adalah -3 ≤ x ≤ -1 atau 1 ≤ x ≤ 3.
-
Soal 5: Tentukan penyelesaian dari pertidaksamaan |x – 1| / |x + 2| > 2.
Solusi:
Pertidaksamaan ini dapat diselesaikan dengan mempertimbangkan dua kasus:
- x + 2 > 0: Dalam kasus ini, pertidaksamaan menjadi (x – 1) / (x + 2) > 2, yang menghasilkan x 0, maka solusi untuk kasus ini adalah -5/3 < x < -2.
- x + 2 < 0: Dalam kasus ini, pertidaksamaan menjadi (x – 1) / (x + 2) -5/3. Karena x + 2 < 0, maka solusi untuk kasus ini adalah -2 < x < -5/3.
Jadi, penyelesaian dari pertidaksamaan ini adalah -5/3 < x < -2.
- a. -5 < x < -1
- b. -1 < x < 5
- c. x -1
- d. x 5
- a. x ≤ -2 atau x ≥ 3
- b. -2 ≤ x ≤ 3
- c. x ≤ -3 atau x ≥ 2
- d. -3 ≤ x ≤ 2
- Grafik fungsi y = |x| adalah bentuk V dengan titik puncak di (0, 0).
- Garis horizontal y = 2 dan y = -2 akan memotong grafik y = |x| di dua titik, yaitu (2, 2) dan (-2, -2).
- Solusi dari pertidaksamaan |x| < 2 adalah semua titik x yang berada di antara garis y = 2 dan y = -2, tidak termasuk titik-titik di garis tersebut.
- Grafik fungsi y = |x – 1| adalah bentuk V yang bergeser 1 satuan ke kanan, dengan titik puncak di (1, 0).
- Garis horizontal y = 3 dan y = -3 akan memotong grafik y = |x – 1| di dua titik.
- Solusi dari pertidaksamaan |x – 1| > 3 adalah semua titik x yang berada di luar garis y = 3 dan y = -3, termasuk titik-titik di garis tersebut.
- Tentukan nilai mutlak dari ekspresi di dalam tanda mutlak. Dalam hal ini, kita perlu mencari nilai 2x – 3 yang menghasilkan nilai mutlak kurang dari 5.
- Karena nilai mutlak selalu positif, maka kita dapat memecah pertidaksamaan menjadi dua kasus:
- Kasus 1: 2x – 3 > 0
- Kasus 2: 2x – 3 < 0
- Selesaikan pertidaksamaan pada setiap kasus:
- Kasus 1: 2x – 3 > 0 ⇒ 2x > 3 ⇒ x > 3/2
- Kasus 2: 2x – 3 < 0 ⇒ 2x < 3 ⇒ x < 3/2
- Gabungkan solusi dari kedua kasus, mengingat batasan nilai mutlak:
- Untuk x > 3/2, maka |2x – 3| = 2x – 3 < 5. ⇒ 2x < 8 ⇒ x < 4
- Untuk x < 3/2, maka |2x – 3| = -(2x – 3) < 5. ⇒ -2x + 3 < 5 ⇒ -2x < 2 ⇒ x > -1
- Himpunan penyelesaian pertidaksamaan tersebut adalah x yang memenuhi -1 < x < 4.
Contoh Soal Pertidaksamaan Nilai Mutlak
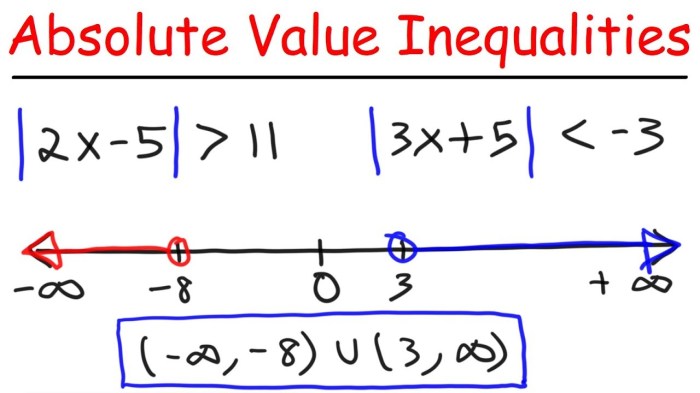
Pertidaksamaan nilai mutlak adalah salah satu topik penting dalam matematika yang mempelajari hubungan antara nilai mutlak suatu ekspresi aljabar dengan suatu nilai atau ekspresi lain. Untuk memahami konsep ini dengan baik, mari kita bahas beberapa contoh soal pertidaksamaan nilai mutlak beserta penyelesaiannya.
Contoh Soal Pertidaksamaan Nilai Mutlak
Berikut ini adalah lima contoh soal pertidaksamaan nilai mutlak dengan tingkat kesulitan yang berbeda. Setiap soal dilengkapi dengan solusi lengkap untuk membantu Anda memahami cara menyelesaikannya.
Contoh Soal Pertidaksamaan Nilai Mutlak Pilihan Ganda
Berikut ini adalah contoh soal pertidaksamaan nilai mutlak dalam bentuk pilihan ganda.
| No | Soal | Pilihan Jawaban | Kunci Jawaban |
|---|---|---|---|
| 1 | Tentukan penyelesaian dari pertidaksamaan |x + 3| < 2. |
|
a |
| 2 | Tentukan penyelesaian dari pertidaksamaan |2x – 1| ≥ 5. |
|
a |
Ilustrasi Grafik Pertidaksamaan Nilai Mutlak
Pertidaksamaan nilai mutlak dapat diilustrasikan dengan grafik, yang membantu kita memahami solusi dari pertidaksamaan tersebut secara visual. Grafik memungkinkan kita melihat rentang nilai yang memenuhi pertidaksamaan.
Ilustrasi Grafik |x| < 2
Untuk pertidaksamaan |x| < 2, kita dapat menggambar grafik fungsi y = |x| dan garis horizontal y = 2. Solusi dari pertidaksamaan ini adalah semua nilai x yang berada di antara garis y = 2 dan y = -2, tidak termasuk titik-titik di garis tersebut.
Ilustrasi Grafik |x – 1| > 3
Pertidaksamaan |x – 1| > 3 dapat diilustrasikan dengan menggambar grafik fungsi y = |x – 1| dan garis horizontal y = 3. Solusi dari pertidaksamaan ini adalah semua nilai x yang berada di luar garis y = 3 dan y = -3, termasuk titik-titik di garis tersebut.
Contoh Soal Pertidaksamaan Nilai Mutlak dan Penyelesaiannya
Pertidaksamaan nilai mutlak merupakan jenis pertidaksamaan yang melibatkan nilai mutlak dari suatu ekspresi aljabar. Untuk menyelesaikan pertidaksamaan nilai mutlak, kita perlu memahami sifat-sifat nilai mutlak dan menerapkannya dalam menyelesaikan pertidaksamaan tersebut.
Contoh Soal Pertidaksamaan Nilai Mutlak dan Penyelesaiannya
Berikut ini adalah contoh soal pertidaksamaan nilai mutlak yang melibatkan operasi aljabar dan langkah-langkah penyelesaiannya:
Soal
Tentukan himpunan penyelesaian dari pertidaksamaan nilai mutlak berikut:
|2x – 3| < 5
Penyelesaian
Relasi Pertidaksamaan Nilai Mutlak, Solusi, dan Representasi Grafik
Berikut adalah tabel yang menunjukkan relasi antara pertidaksamaan nilai mutlak, solusi, dan representasi grafiknya:
| Pertidaksamaan Nilai Mutlak | Solusi | Representasi Grafik |
|---|---|---|
| |x| < a | -a < x < a | Garis bilangan dengan titik terbuka pada -a dan a, dan daerah yang diarsir di antara kedua titik tersebut. |
| |x| > a | x < -a atau x > a | Garis bilangan dengan titik terbuka pada -a dan a, dan daerah yang diarsir di luar kedua titik tersebut. |
| |x| ≤ a | -a ≤ x ≤ a | Garis bilangan dengan titik tertutup pada -a dan a, dan daerah yang diarsir di antara kedua titik tersebut. |
| |x| ≥ a | x ≤ -a atau x ≥ a | Garis bilangan dengan titik tertutup pada -a dan a, dan daerah yang diarsir di luar kedua titik tersebut. |
Penerapan Pertidaksamaan Nilai Mutlak dalam Kehidupan Sehari-hari
Pertidaksamaan nilai mutlak, selain memiliki peran penting dalam matematika, ternyata juga memiliki aplikasi yang luas dalam kehidupan sehari-hari. Konsep ini dapat membantu kita dalam menyelesaikan masalah yang melibatkan toleransi, batas, dan ketidakpastian, khususnya dalam bidang industri, bisnis, dan keuangan.
Batas Toleransi dalam Produksi
Pertidaksamaan nilai mutlak dapat digunakan untuk menentukan batas toleransi dalam produksi. Misalkan, sebuah pabrik memproduksi baut dengan panjang standar 10 cm. Namun, dalam proses produksi, tidak mungkin semua baut memiliki panjang persis 10 cm. Terdapat toleransi yang diizinkan, misalnya, 0,1 cm. Artinya, panjang baut yang diproduksi dapat bervariasi antara 9,9 cm dan 10,1 cm.
Kita dapat menggunakan pertidaksamaan nilai mutlak untuk merepresentasikan toleransi ini. Jika x adalah panjang baut yang diproduksi, maka pertidaksamaan nilai mutlak yang mewakili toleransi tersebut adalah:
|x – 10| ≤ 0,1
Pertidaksamaan ini menyatakan bahwa selisih antara panjang baut yang diproduksi (x) dan panjang standar (10 cm) tidak boleh melebihi 0,1 cm. Dengan menyelesaikan pertidaksamaan ini, kita dapat menentukan rentang panjang baut yang masih memenuhi toleransi.
Contoh Skenario dalam Bisnis atau Keuangan
Bayangkan Anda adalah seorang manajer keuangan yang ingin menentukan batas maksimum kerugian yang dapat ditanggung oleh perusahaan dalam suatu investasi. Anda memperkirakan bahwa keuntungan investasi dapat bervariasi antara 10% hingga 20%, tetapi juga ada kemungkinan kerugian hingga 5%. Anda ingin menetapkan batas maksimum kerugian yang dapat ditanggung perusahaan agar tidak mengalami kerugian yang terlalu besar.
Pertidaksamaan nilai mutlak dapat membantu Anda dalam menentukan batas maksimum kerugian. Misalkan x adalah tingkat pengembalian investasi, maka pertidaksamaan nilai mutlak yang mewakili batas maksimum kerugian adalah:
|x – 10| ≤ 5
Pertidaksamaan ini menyatakan bahwa selisih antara tingkat pengembalian investasi (x) dan keuntungan minimum (10%) tidak boleh melebihi 5%. Dengan menyelesaikan pertidaksamaan ini, Anda dapat menentukan batas maksimum kerugian yang dapat ditanggung perusahaan, yaitu 5%.
Contoh Soal
Sebuah perusahaan elektronik memproduksi resistor dengan nilai resistansi standar 100 ohm. Dalam proses produksi, toleransi yang diizinkan adalah 5%. Seorang teknisi ingin menguji resistor yang baru diproduksi. Ia mengukur nilai resistansi resistor tersebut dan mendapatkan hasil 103 ohm. Apakah resistor tersebut memenuhi toleransi yang diizinkan?
Untuk menyelesaikan masalah ini, kita dapat menggunakan pertidaksamaan nilai mutlak. Jika x adalah nilai resistansi resistor yang diproduksi, maka pertidaksamaan nilai mutlak yang mewakili toleransi tersebut adalah:
|x – 100| ≤ 5
Kita perlu menentukan apakah nilai resistansi yang diukur (103 ohm) memenuhi pertidaksamaan ini. Kita substitusikan nilai x = 103 ke dalam pertidaksamaan:
|103 – 100| ≤ 5
|3| ≤ 5
Karena nilai mutlak dari 3 adalah 3, dan 3 ≤ 5, maka resistor tersebut memenuhi toleransi yang diizinkan.
Contoh Soal Pertidaksamaan Nilai Mutlak dalam Bidang Lainnya
Pertidaksamaan nilai mutlak tidak hanya terbatas pada matematika murni, tetapi juga memiliki aplikasi luas dalam berbagai bidang ilmu pengetahuan.
Penerapan Pertidaksamaan Nilai Mutlak dalam Fisika, Contoh soal pertidaksamaan nilai mutlak dan penyelesaiannya
Pertidaksamaan nilai mutlak dapat digunakan dalam fisika untuk menghitung jarak minimum antara dua benda. Misalnya, dalam fisika atom, pertidaksamaan nilai mutlak dapat digunakan untuk menentukan jarak minimum antara elektron dan inti atom.
Penerapan Pertidaksamaan Nilai Mutlak dalam Kimia
Pertidaksamaan nilai mutlak dapat digunakan dalam kimia untuk menghitung konsentrasi larutan. Misalnya, pertidaksamaan nilai mutlak dapat digunakan untuk menentukan konsentrasi minimum suatu zat dalam larutan agar reaksi kimia tertentu dapat terjadi.
Contoh Soal Pertidaksamaan Nilai Mutlak dalam Berbagai Bidang Ilmu Pengetahuan
Berikut tabel yang menunjukkan berbagai contoh soal pertidaksamaan nilai mutlak dalam berbagai bidang ilmu pengetahuan:
| Bidang Ilmu Pengetahuan | Contoh Soal |
|---|---|
| Fisika | Sebuah partikel bergerak dengan kecepatan v. Jika jarak minimum antara partikel tersebut dengan titik acuan adalah d, maka tentukan persamaan pertidaksamaan nilai mutlak yang menyatakan jarak antara partikel tersebut dengan titik acuan. |
| Kimia | Sebuah larutan mengandung zat A dengan konsentrasi x. Jika konsentrasi minimum zat A yang diperlukan untuk reaksi kimia tertentu adalah c, maka tentukan persamaan pertidaksamaan nilai mutlak yang menyatakan konsentrasi zat A dalam larutan. |
| Biologi | Sebuah populasi bakteri berkembang biak dengan laju r. Jika populasi minimum bakteri yang diperlukan untuk memicu penyakit adalah p, maka tentukan persamaan pertidaksamaan nilai mutlak yang menyatakan populasi bakteri setelah waktu t. |
| Ekonomi | Sebuah perusahaan memproduksi barang dengan biaya tetap c dan biaya variabel per unit b. Jika harga jual per unit adalah p, maka tentukan persamaan pertidaksamaan nilai mutlak yang menyatakan keuntungan perusahaan. |
Ulasan Penutup: Contoh Soal Pertidaksamaan Nilai Mutlak Dan Penyelesaiannya
Melalui contoh soal dan penjelasan yang komprehensif, kita telah mempelajari bagaimana menyelesaikan pertidaksamaan nilai mutlak dengan berbagai metode. Dengan pemahaman yang kuat tentang konsep ini, kamu dapat menerapkannya untuk memecahkan masalah dalam berbagai bidang, mulai dari ilmu pengetahuan hingga kehidupan sehari-hari.





