Contoh soal poset – Pernahkah Anda mendengar istilah “poset”? Mungkin terdengar asing, tapi sebenarnya poset adalah konsep matematika yang menarik dan memiliki banyak aplikasi dalam kehidupan sehari-hari. Poset, singkatan dari “partially ordered set”, adalah himpunan yang dilengkapi dengan relasi “kurang dari atau sama dengan” yang memenuhi beberapa sifat khusus.
Dalam artikel ini, kita akan menjelajahi dunia poset dengan berbagai contoh soal yang menantang. Mulai dari pengertian dasar hingga aplikasi poset dalam bidang komputer dan ekonomi, kita akan mempelajari bagaimana poset dapat membantu kita memahami dan menyelesaikan masalah dengan lebih efektif.
Pengertian Poset
Poset, singkatan dari Partially Ordered Set, adalah suatu himpunan yang dilengkapi dengan relasi khusus yang disebut relasi parsial. Relasi ini memungkinkan kita untuk membandingkan elemen-elemen dalam himpunan tersebut, namun tidak semua elemen harus dapat dibandingkan satu sama lain.
Contoh soal poset seringkali melibatkan diagram Hasse, yang menunjukkan hubungan antara elemen-elemen dalam suatu himpunan. Nah, untuk memahami lebih dalam tentang diagram Hasse, kamu bisa latihan dengan contoh soal merasionalkan bentuk akar kelas 9 seperti yang dibahas di contoh soal merasionalkan bentuk akar kelas 9.
Konsep ini mungkin terlihat berbeda, tapi sebenarnya keduanya saling berkaitan dalam membangun pemahaman tentang matematika yang lebih luas.
Contoh Poset Sederhana
Bayangkan sebuah himpunan A yang terdiri dari angka 1, 2, 3, dan 4. Relasi parsial yang kita gunakan adalah “kurang dari atau sama dengan” (≤). Dengan relasi ini, kita dapat mengatakan bahwa 1 ≤ 2, 2 ≤ 3, dan 3 ≤ 4. Namun, kita tidak dapat membandingkan angka 2 dan 4 karena keduanya tidak “kurang dari atau sama dengan” satu sama lain.
Poset ini dapat direpresentasikan dalam diagram Hasse, yang merupakan diagram khusus untuk menunjukkan relasi parsial. Dalam diagram Hasse, elemen yang lebih tinggi menunjukkan elemen yang lebih besar dalam relasi.
Berikut adalah contoh diagram Hasse untuk poset (A, ≤):
Gambar: Diagram Hasse dengan elemen 1, 2, 3, dan 4, dengan 1 di bagian bawah, 2 di atas 1, 3 di atas 2, dan 4 di atas 3. Garis menghubungkan elemen yang berhubungan.
Contoh Poset dalam Kehidupan Sehari-hari
Poset sering dijumpai dalam kehidupan sehari-hari, berikut beberapa contohnya:
- Himpunan semua buku di perpustakaan, dengan relasi “diterbitkan sebelum”. Buku yang diterbitkan lebih awal dianggap “lebih kecil” dalam relasi ini.
- Himpunan semua karyawan di sebuah perusahaan, dengan relasi “mengawasi”. Manajer dianggap “lebih besar” dalam relasi ini karena mengawasi karyawan lain.
- Himpunan semua tugas yang harus diselesaikan, dengan relasi “harus diselesaikan sebelum”. Tugas yang harus diselesaikan terlebih dahulu dianggap “lebih kecil” dalam relasi ini.
Sifat-Sifat Poset
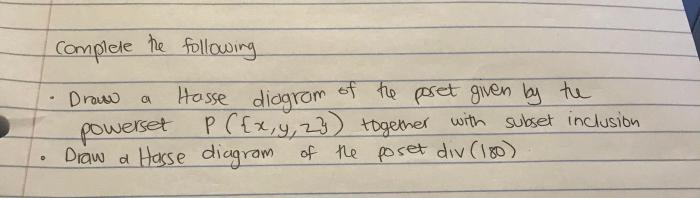
Setelah kita memahami konsep poset (partially ordered set) dan contohnya, sekarang kita akan membahas sifat-sifat penting yang dimiliki oleh poset. Sifat-sifat ini membantu kita dalam mengklasifikasikan dan menganalisis poset, serta memahami bagaimana elemen-elemen di dalamnya saling berhubungan.
Sifat Refleksif
Sifat refleksif menyatakan bahwa setiap elemen dalam poset berhubungan dengan dirinya sendiri. Dengan kata lain, setiap elemen adalah relasi dengan dirinya sendiri. Secara formal, sifat refleksif dapat dituliskan sebagai:
a ≤ a, untuk setiap a ∈ P
Contoh poset yang memenuhi sifat refleksif adalah himpunan bilangan bulat positif dengan relasi “kurang dari atau sama dengan” (≤). Setiap bilangan bulat positif selalu kurang dari atau sama dengan dirinya sendiri.
Contoh poset yang tidak memenuhi sifat refleksif adalah himpunan bilangan bulat positif dengan relasi “lebih dari” (>). Karena setiap bilangan bulat positif tidak lebih dari dirinya sendiri.
Sifat Antisimetrik
Sifat antisimetrik menyatakan bahwa jika dua elemen dalam poset saling berhubungan, maka hanya ada satu relasi yang berlaku. Dengan kata lain, jika a ≤ b dan b ≤ a, maka a = b. Secara formal, sifat antisimetrik dapat dituliskan sebagai:
Jika a ≤ b dan b ≤ a, maka a = b, untuk setiap a, b ∈ P
Contoh poset yang memenuhi sifat antisimetrik adalah himpunan bilangan bulat positif dengan relasi “kurang dari atau sama dengan” (≤). Jika a ≤ b dan b ≤ a, maka a = b.
Contoh poset yang tidak memenuhi sifat antisimetrik adalah himpunan bilangan bulat positif dengan relasi “faktor dari” (|). Contohnya, 2 | 4 dan 4 | 2, tetapi 2 ≠ 4.
Sifat Transitif
Sifat transitif menyatakan bahwa jika a ≤ b dan b ≤ c, maka a ≤ c. Secara formal, sifat transitif dapat dituliskan sebagai:
Jika a ≤ b dan b ≤ c, maka a ≤ c, untuk setiap a, b, c ∈ P
Contoh poset yang memenuhi sifat transitif adalah himpunan bilangan bulat positif dengan relasi “kurang dari atau sama dengan” (≤). Jika a ≤ b dan b ≤ c, maka a ≤ c.
Contoh poset yang tidak memenuhi sifat transitif adalah himpunan bilangan bulat positif dengan relasi “lebih dari” (>). Karena jika a > b dan b > c, maka a tidak selalu lebih dari c.
Diagram Hasse
Diagram Hasse merupakan representasi visual dari poset (partially ordered set) yang sederhana dan mudah dipahami. Diagram ini membantu kita memahami hubungan keterurutan antar elemen dalam poset dengan cara yang lebih intuitif.
Cara Membuat Diagram Hasse
Untuk membuat diagram Hasse dari suatu poset, kita perlu mengikuti langkah-langkah berikut:
- Tentukan elemen-elemen poset dan hubungan keterurutannya.
- Gambar titik-titik yang mewakili elemen-elemen poset.
- Hubungkan dua titik dengan garis jika satu elemen merupakan elemen langsung atas dari elemen lainnya.
- Elemen yang lebih kecil digambar di bagian bawah diagram, sedangkan elemen yang lebih besar digambar di bagian atas.
- Hindari garis silang dan garis yang tidak perlu, karena diagram Hasse harus mudah dibaca dan dipahami.
Contoh Diagram Hasse
Berikut adalah beberapa contoh diagram Hasse untuk poset sederhana:
- Poset dengan elemen a, b, c, d dan hubungan keterurutan a < b, a < c, a < d, b < d, c < d.
Diagram Hasse-nya adalah:

Dalam diagram ini, titik-titik mewakili elemen poset, dan garis-garis menunjukkan hubungan keterurutan langsung. Misalnya, garis dari titik a ke titik b menunjukkan bahwa a merupakan elemen langsung atas dari b. - Poset dengan elemen 1, 2, 3, 4, 6, 12 dan hubungan keterurutan “membagi” (misalnya, 2 membagi 4).
Diagram Hasse-nya adalah:

Dalam diagram ini, kita dapat melihat bahwa 1 merupakan elemen terkecil, sedangkan 12 merupakan elemen terbesar.
Hubungan Elemen Poset dan Diagram Hasse
Tabel berikut menunjukkan hubungan antara elemen poset dan diagram Hasse-nya:
| Elemen Poset | Diagram Hasse |
|---|---|
| a | Titik yang paling bawah |
| b | Titik yang terhubung langsung ke a |
| c | Titik yang terhubung langsung ke a |
| d | Titik yang terhubung langsung ke b dan c |
Jenis-Jenis Poset
Setelah memahami definisi dan contoh poset, mari kita bahas beberapa jenis poset yang umum ditemui. Jenis-jenis poset ini memiliki karakteristik dan sifat khusus yang membedakannya satu sama lain.
Poset Rantai
Poset rantai, atau yang sering disebut poset total, adalah poset di mana setiap dua elemennya dapat dibandingkan. Artinya, untuk setiap dua elemen a dan b dalam poset, selalu berlaku a ≤ b atau b ≤ a.
- Contoh: Himpunan bilangan bulat 1, 2, 3, 4 dengan relasi ≤ adalah poset rantai.
- Karakteristik: Poset rantai memiliki sifat bahwa setiap subsetnya juga merupakan poset rantai.
Poset Antirantai
Berbeda dengan poset rantai, poset antirantai adalah poset di mana tidak ada dua elemen yang dapat dibandingkan. Artinya, untuk setiap dua elemen a dan b dalam poset, a ≤ b dan b ≤ a tidak berlaku.
- Contoh: Himpunan a, b, c dengan relasi a ≤ b, b ≤ c, dan c ≤ a tidak berlaku.
- Karakteristik: Poset antirantai memiliki sifat bahwa setiap subsetnya juga merupakan poset antirantai.
Poset Lattice
Poset lattice adalah poset yang memiliki sifat khusus:
- Setiap dua elemen memiliki supremum (least upper bound) dan infimum (greatest lower bound).
- Supremum dari dua elemen a dan b adalah elemen terkecil yang lebih besar atau sama dengan a dan b.
- Infimum dari dua elemen a dan b adalah elemen terbesar yang lebih kecil atau sama dengan a dan b.
Contoh: Himpunan 1, 2, 3, 4, 6, 12 dengan relasi “membagi” adalah poset lattice. Supremum dari 2 dan 3 adalah 6, sedangkan infimumnya adalah 1.
Tabel Jenis-Jenis Poset
| Jenis Poset | Contoh | Karakteristik |
|---|---|---|
| Poset Rantai | Himpunan bilangan bulat 1, 2, 3, 4 dengan relasi ≤ | Setiap dua elemen dapat dibandingkan. |
| Poset Antirantai | Himpunan a, b, c dengan relasi a ≤ b, b ≤ c, dan c ≤ a tidak berlaku. | Tidak ada dua elemen yang dapat dibandingkan. |
| Poset Lattice | Himpunan 1, 2, 3, 4, 6, 12 dengan relasi “membagi” | Setiap dua elemen memiliki supremum dan infimum. |
Aplikasi Poset
Poset, singkatan dari “partially ordered set”, adalah struktur matematika yang menggambarkan hubungan ketertiban parsial antara elemen-elemen dalam suatu himpunan. Hubungan ketertiban parsial ini memiliki sifat-sifat tertentu, seperti refleksif, antisimetrik, dan transitif. Poset memiliki banyak aplikasi di berbagai bidang, mulai dari matematika dan ilmu komputer hingga kehidupan sehari-hari. Berikut beberapa contoh aplikasi poset:
Aplikasi Poset dalam Matematika
Poset memainkan peran penting dalam berbagai cabang matematika, seperti teori himpunan, aljabar, dan topologi.
- Dalam teori himpunan, poset digunakan untuk mengklasifikasikan himpunan berdasarkan relasi inklusi. Misalnya, himpunan 1, 2 adalah subset dari 1, 2, 3, sehingga 1, 2 ≤ 1, 2, 3 dalam poset yang dibentuk oleh relasi inklusi.
- Dalam aljabar, poset digunakan untuk mempelajari struktur aljabar, seperti grup, ring, dan modul.
- Dalam topologi, poset digunakan untuk mempelajari ruang topologi, seperti ruang metrik dan ruang topologi lainnya.
Aplikasi Poset dalam Ilmu Komputer
Poset memiliki banyak aplikasi dalam ilmu komputer, terutama dalam bidang algoritma, struktur data, dan pemodelan sistem.
- Dalam algoritma, poset digunakan untuk merancang algoritma yang efisien untuk memecahkan masalah tertentu, seperti pencocokan pola dan pencarian jalur terpendek.
- Dalam struktur data, poset digunakan untuk mengimplementasikan struktur data yang efisien, seperti pohon pencarian biner dan heap.
- Dalam pemodelan sistem, poset digunakan untuk memodelkan hubungan ketergantungan antara komponen sistem, seperti dependensi antar modul program atau hubungan antar proses dalam sistem operasi.
Aplikasi Poset dalam Kehidupan Sehari-hari
Poset juga memiliki aplikasi yang nyata dalam kehidupan sehari-hari.
- Contohnya, dalam manajemen proyek, poset dapat digunakan untuk memodelkan ketergantungan antar tugas. Misalnya, tugas A harus diselesaikan sebelum tugas B dapat dimulai, sehingga tugas A ≤ tugas B dalam poset yang dibentuk oleh relasi ketergantungan.
- Poset juga dapat digunakan dalam pengambilan keputusan, untuk mengurutkan preferensi atau prioritas. Misalnya, dalam memilih menu makanan, kita dapat menggunakan poset untuk mengurutkan preferensi kita terhadap berbagai hidangan.
- Dalam desain web, poset dapat digunakan untuk memodelkan hierarki konten atau navigasi website.
Contoh Soal Poset dan Pembahasan
Poset (Partially Ordered Set) merupakan struktur matematika yang sangat berguna dalam berbagai bidang seperti ilmu komputer, teori himpunan, dan logika. Dalam poset, elemen-elemennya diurutkan secara parsial, artinya tidak semua elemen dapat dibandingkan secara langsung. Untuk memahami konsep poset, kita akan membahas contoh soal berikut.
Soal Poset dan Pembahasan
Misalkan kita diberikan himpunan S = 1, 2, 3, 4, 6, 12 dengan relasi “membagi” (aRb jika a membagi b). Apakah (S, R) merupakan poset? Jika ya, gambarkan diagram Hasse-nya.
Langkah-langkah Penyelesaian
- Memeriksa sifat-sifat poset:
- Refleksif: Setiap elemen harus membagi dirinya sendiri. Dalam kasus ini, setiap elemen di S membagi dirinya sendiri, sehingga sifat refleksif terpenuhi.
- Antisimetris: Jika a membagi b dan b membagi a, maka a harus sama dengan b. Dalam kasus ini, jika a membagi b dan b membagi a, maka a dan b haruslah sama, sehingga sifat antisimetris terpenuhi.
- Transitif: Jika a membagi b dan b membagi c, maka a harus membagi c. Dalam kasus ini, jika a membagi b dan b membagi c, maka a juga membagi c, sehingga sifat transitif terpenuhi.
Karena ketiga sifat poset terpenuhi, maka (S, R) merupakan poset.
- Menggambar diagram Hasse:
Diagram Hasse adalah representasi grafis dari poset yang menunjukkan hubungan antara elemen-elemennya. Untuk menggambar diagram Hasse, kita perlu memperhatikan beberapa hal:
- Elemen terkecil ditempatkan di bagian bawah diagram.
- Elemen terbesar ditempatkan di bagian atas diagram.
- Hubungan “membagi” digambarkan dengan garis yang menghubungkan elemen yang lebih kecil ke elemen yang lebih besar.
- Garis tidak boleh berpotongan.
Berikut adalah diagram Hasse untuk poset (S, R):
Diagram Hasse menggambarkan hubungan pembagian antara elemen-elemen dalam himpunan S. Misalnya, garis yang menghubungkan 1 dan 2 menunjukkan bahwa 1 membagi 2, garis yang menghubungkan 2 dan 4 menunjukkan bahwa 2 membagi 4, dan seterusnya.
Konsep dan Prinsip yang Digunakan
- Pengertian Poset: Poset adalah himpunan yang dilengkapi dengan relasi urutan parsial, yaitu relasi yang memenuhi sifat refleksif, antisimetris, dan transitif.
- Diagram Hasse: Diagram Hasse adalah representasi grafis dari poset yang menunjukkan hubungan antara elemen-elemennya.
- Relasi “Membagi”: Relasi “membagi” dalam contoh soal ini adalah relasi urutan parsial yang digunakan untuk menentukan hubungan antara elemen-elemen dalam himpunan S.
Contoh Soal Poset dengan Diagram Hasse
Poset (partially ordered set) merupakan himpunan yang dilengkapi dengan relasi ketertiban parsial. Diagram Hasse merupakan representasi visual dari poset yang menunjukkan hubungan antara elemen-elemennya. Diagram Hasse dapat digunakan untuk mempermudah pemahaman tentang relasi poset dan untuk memecahkan masalah yang terkait dengan poset.
Menentukan Relasi Poset dari Diagram Hasse
Berikut ini adalah contoh soal yang melibatkan diagram Hasse dan meminta siswa untuk menentukan relasi poset dari diagram tersebut:
Soal:
Perhatikan diagram Hasse berikut:
[Gambar Diagram Hasse dengan elemen A, B, C, D, E, F, dan G]
Tentukan relasi poset dari diagram Hasse tersebut.
Penyelesaian:
Relasi poset dari diagram Hasse dapat ditentukan dengan melihat hubungan antara elemen-elemennya. Elemen yang berada di atas elemen lain dalam diagram Hasse memiliki relasi “lebih besar dari” terhadap elemen di bawahnya.
Misalnya, elemen A berada di atas elemen B, sehingga A > B. Demikian juga, elemen C berada di atas elemen B, sehingga C > B.
Dengan demikian, relasi poset dari diagram Hasse tersebut adalah:
* A > B
* A > C
* A > D
* A > E
* A > F
* A > G
* B > D
* B > E
* B > F
* B > G
* C > D
* C > E
* C > F
* C > G
* D > F
* D > G
* E > F
* E > G
* F > G
Ilustrasi Diagram Hasse
Diagram Hasse dapat digunakan untuk menggambarkan hubungan antara elemen-elemen poset. Berikut adalah contoh ilustrasi diagram Hasse yang menunjukkan hubungan antara elemen poset:
Contoh:
Misalkan diberikan himpunan S = a, b, c, d dengan relasi poset R = (a, a), (b, b), (c, c), (d, d), (a, b), (a, c), (a, d), (b, d). Diagram Hasse untuk poset (S, R) dapat digambarkan sebagai berikut:
[Gambar Diagram Hasse dengan elemen a, b, c, d]
Dalam diagram Hasse ini, elemen a berada di atas elemen b, c, dan d. Hal ini menunjukkan bahwa a “lebih besar dari” b, c, dan d. Elemen b dan c berada di atas elemen d, sehingga b dan c “lebih besar dari” d.
Cara Menentukan Relasi Poset dari Diagram Hasse
Untuk menentukan relasi poset dari diagram Hasse, ikuti langkah-langkah berikut:
1. Identifikasi elemen-elemen poset.
2. Tentukan hubungan antara elemen-elemen. Elemen yang berada di atas elemen lain memiliki relasi “lebih besar dari” terhadap elemen di bawahnya.
3. Buatlah daftar relasi poset. Daftar ini akan berisi semua pasangan elemen yang memiliki relasi “lebih besar dari” dalam diagram Hasse.
Dengan mengikuti langkah-langkah ini, Anda dapat dengan mudah menentukan relasi poset dari diagram Hasse.
Soal Poset dengan Aplikasi
Poset, atau himpunan terurut sebagian, merupakan konsep penting dalam matematika yang memiliki aplikasi luas dalam berbagai bidang, seperti ilmu komputer, ekonomi, dan teori keputusan. Dalam konteks ini, kita akan membahas bagaimana poset dapat digunakan untuk menyelesaikan masalah di bidang-bidang tersebut.
Contoh Soal Poset dalam Ilmu Komputer
Poset dapat digunakan untuk memodelkan hubungan antar elemen dalam struktur data seperti pohon biner. Misalnya, dalam pohon biner, setiap simpul dapat dihubungkan ke simpul lainnya melalui relasi “anak” atau “turunan”. Relasi ini membentuk poset, karena setiap simpul memiliki satu atau lebih anak, dan relasi “anak” bersifat transitif (jika A adalah anak dari B, dan B adalah anak dari C, maka A adalah anak dari C).
Aplikasi Poset dalam Pencarian Data
Poset dapat membantu dalam pencarian data dalam struktur data seperti pohon biner. Misalnya, dalam algoritma pencarian biner, data diurutkan dalam pohon biner, dan pencarian dilakukan dengan membandingkan nilai data target dengan nilai data di simpul akar. Jika nilai target lebih kecil dari nilai data di simpul akar, pencarian dilanjutkan ke sub-pohon kiri, dan sebaliknya. Proses ini berulang hingga nilai target ditemukan atau pohon biner habis.
Contoh Soal Poset dalam Ekonomi
Poset dapat digunakan untuk memodelkan preferensi konsumen dalam ekonomi. Misalnya, konsumen mungkin memiliki preferensi terhadap berbagai jenis barang atau jasa, dan preferensi ini dapat diurutkan secara parsial. Relasi “lebih disukai” membentuk poset, karena preferensi bersifat transitif (jika A lebih disukai dari B, dan B lebih disukai dari C, maka A lebih disukai dari C).
Aplikasi Poset dalam Analisis Preferensi Konsumen
Poset dapat membantu dalam analisis preferensi konsumen. Misalnya, dalam analisis preferensi konsumen, poset dapat digunakan untuk mengidentifikasi pola preferensi dan menentukan preferensi yang dominan. Poset juga dapat digunakan untuk memodelkan perilaku konsumen dalam situasi di mana pilihan mereka dibatasi oleh anggaran atau keterbatasan lainnya.
Contoh Kasus Nyata
Sebagai contoh, perhatikan sebuah perusahaan yang menjual berbagai jenis produk. Perusahaan ingin memodelkan preferensi pelanggan terhadap produk mereka. Mereka dapat menggunakan poset untuk memodelkan hubungan “lebih disukai” antara produk-produk tersebut. Misalnya, pelanggan mungkin lebih menyukai produk A daripada produk B, dan produk B lebih disukai daripada produk C. Relasi ini membentuk poset, dan perusahaan dapat menggunakan poset untuk menganalisis preferensi pelanggan dan menentukan produk mana yang paling diminati.
Soal Poset dengan Pembahasan Berlangkah
Dalam dunia matematika, Poset (Partially Ordered Set) merupakan struktur yang menarik dan memiliki banyak aplikasi dalam berbagai bidang seperti ilmu komputer, teori himpunan, dan teori kisi. Untuk memahami Poset dengan lebih baik, kita perlu berlatih dengan soal-soal yang menantang. Berikut adalah contoh soal Poset dengan pembahasan langkah demi langkah.
Soal Poset, Contoh soal poset
Diberikan himpunan A = 1, 2, 3, 4, 5 dengan relasi R = (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5). Apakah (A, R) merupakan Poset? Jelaskan dan tunjukkan diagram Hasse-nya.
Pembahasan Berlangkah
Untuk menentukan apakah (A, R) merupakan Poset, kita perlu memeriksa apakah relasi R memenuhi sifat-sifat berikut:
- Refleksif: Untuk setiap a ∈ A, (a, a) ∈ R.
- Antisimetris: Jika (a, b) ∈ R dan (b, a) ∈ R, maka a = b.
- Transitif: Jika (a, b) ∈ R dan (b, c) ∈ R, maka (a, c) ∈ R.
Mari kita periksa sifat-sifat tersebut satu per satu:
1. Refleksif
Dari definisi relasi R, kita dapat melihat bahwa (1, 1), (2, 2), (3, 3), (4, 4), dan (5, 5) semuanya termasuk dalam R. Hal ini menunjukkan bahwa untuk setiap elemen a ∈ A, (a, a) ∈ R. Jadi, relasi R bersifat refleksif.
2. Antisimetris
Perhatikan bahwa (1, 2) ∈ R dan (2, 1) ∉ R. Ini berarti bahwa meskipun (a, b) ∈ R dan (b, a) ∈ R, tidak selalu berarti a = b. Jadi, relasi R tidak bersifat antisimetris.
3. Transitif
Misalnya, (1, 2) ∈ R dan (2, 3) ∈ R. Kita juga dapat melihat bahwa (1, 3) ∈ R. Hal ini menunjukkan bahwa jika (a, b) ∈ R dan (b, c) ∈ R, maka (a, c) ∈ R. Jadi, relasi R bersifat transitif.
Karena relasi R tidak bersifat antisimetris, maka (A, R) bukanlah Poset.
Diagram Hasse
Meskipun (A, R) bukan Poset, kita tetap dapat menggambar diagram Hasse-nya. Diagram Hasse adalah representasi grafis dari Poset yang menunjukkan hubungan antara elemen-elemennya. Untuk menggambar diagram Hasse, kita perlu:
- Menampilkan setiap elemen dalam himpunan A sebagai titik.
- Menggambar garis yang menghubungkan dua titik jika ada relasi langsung antara elemen-elemen tersebut.
- Menempatkan elemen yang lebih kecil di bawah elemen yang lebih besar.
Diagram Hasse untuk (A, R) adalah sebagai berikut:
[Gambar ilustrasi diagram Hasse dengan elemen-elemen 1, 2, 3, 4, dan 5. Garis menghubungkan 1 ke 2, 1 ke 3, 1 ke 4, 1 ke 5, 2 ke 3, 2 ke 4, 2 ke 5, 3 ke 4, dan 3 ke 5. Elemen 1 berada di bagian paling bawah, diikuti oleh 2, 3, 4, dan 5 di bagian paling atas.]
Dalam diagram Hasse ini, kita dapat melihat bahwa relasi R tidak bersifat antisimetris karena terdapat jalur dua arah antara elemen 1 dan 2.
Kesimpulannya, (A, R) bukan Poset karena tidak memenuhi sifat antisimetris. Namun, kita masih dapat menggambar diagram Hasse-nya untuk merepresentasikan relasi R.
Soal Poset dengan Variasi Tingkat Kesulitan: Contoh Soal Poset
Poset (Partially Ordered Set) adalah struktur matematika yang digunakan untuk memodelkan hubungan keteraturan antara elemen-elemen dalam suatu himpunan. Dalam poset, tidak semua elemen harus dapat dibandingkan, namun jika dua elemen dapat dibandingkan, maka hubungan keteraturannya harus bersifat transitif. Soal poset dapat dibedakan berdasarkan tingkat kesulitannya, mulai dari soal yang mudah hingga soal yang sulit. Soal yang mudah biasanya hanya melibatkan pemahaman dasar tentang poset, sedangkan soal yang sulit melibatkan pemahaman yang lebih dalam tentang konsep poset, seperti rantai, antirantai, dan diagram Hasse.
Tingkat Kesulitan Soal Poset
Tingkat kesulitan soal poset dapat dibedakan berdasarkan beberapa faktor, antara lain:
- Kompleksitas poset yang dilibatkan
- Jenis hubungan keteraturan yang dilibatkan
- Jumlah elemen dalam poset
- Konsep poset yang diuji
Contoh Soal Poset dengan Berbagai Tingkat Kesulitan
Berikut ini adalah contoh soal poset dengan berbagai tingkat kesulitan:
Mudah
- Diberikan himpunan A = 1, 2, 3, 4, 5 dengan hubungan keteraturan “lebih kecil dari atau sama dengan”. Apakah (A, ≤) merupakan poset? Jelaskan jawaban Anda.
Sedang
- Diberikan himpunan B = a, b, c, d dengan hubungan keteraturan R = (a, a), (b, b), (c, c), (d, d), (a, b), (a, c), (b, c), (b, d). Buatlah diagram Hasse dari poset (B, R). Tentukan rantai terpanjang dan antirantai terpanjang dalam poset tersebut.
Sulit
- Diberikan poset (P, ≤) dengan diagram Hasse seperti pada gambar di bawah ini. Tentukan jumlah rantai terpanjang dan antirantai terpanjang dalam poset tersebut.
Gambar diagram Hasse poset (P, ≤)
Diagram Hasse menunjukkan hubungan keteraturan antara elemen-elemen dalam poset. Elemen yang lebih tinggi berada di atas elemen yang lebih rendah. Garis yang menghubungkan dua elemen menunjukkan hubungan keteraturan antara keduanya. Misalnya, elemen a ≤ b, c ≤ d, dan a ≤ d.
Soal Poset dengan Pembahasan Lengkap
Poset (Partially Ordered Set) merupakan struktur matematika yang penting dalam berbagai bidang, seperti teori himpunan, aljabar, dan ilmu komputer. Dalam soal poset, kita dihadapkan pada himpunan yang dilengkapi dengan relasi urutan parsial, yang memungkinkan kita untuk menganalisis hubungan antar elemen dalam himpunan tersebut.
Contoh Soal Poset
Misalkan diberikan himpunan S = 1, 2, 3, 4, 5, 6 dengan relasi urutan parsial R yang didefinisikan sebagai “a R b jika dan hanya jika a habis dibagi b”. Tentukan:
- Apakah (S, R) merupakan poset?
- Tentukan diagram Hasse untuk (S, R).
- Tentukan elemen minimal, elemen maksimal, elemen terbesar, dan elemen terkecil dari (S, R).
- Tentukan rantai dan antirantai terpanjang dari (S, R).
Pembahasan Soal Poset
Mari kita bahas setiap pertanyaan secara detail:
Apakah (S, R) merupakan poset?
Untuk menentukan apakah (S, R) merupakan poset, kita perlu memeriksa apakah relasi R memenuhi sifat-sifat relasi urutan parsial, yaitu:
- Refleksif: Untuk setiap elemen a dalam S, a R a.
- Antisimetrik: Jika a R b dan b R a, maka a = b.
- Transitif: Jika a R b dan b R c, maka a R c.
Mari kita periksa satu per satu:
- Refleksif: Untuk setiap elemen a dalam S, a habis dibagi a. Jadi, sifat refleksif terpenuhi.
- Antisimetrik: Jika a habis dibagi b dan b habis dibagi a, maka a = b. Jadi, sifat antisimetrik terpenuhi.
- Transitif: Jika a habis dibagi b dan b habis dibagi c, maka a habis dibagi c. Jadi, sifat transitif terpenuhi.
Karena relasi R memenuhi ketiga sifat relasi urutan parsial, maka (S, R) merupakan poset.
Diagram Hasse untuk (S, R)
Diagram Hasse adalah representasi grafis dari poset yang menunjukkan hubungan urutan parsial antara elemen-elemen dalam poset. Dalam diagram Hasse, setiap elemen diwakili oleh titik, dan garis menghubungkan dua titik jika satu elemen menutupi elemen lainnya. Elemen a menutupi elemen b jika a R b dan tidak ada elemen c dalam S yang memenuhi a R c dan c R b.
Berikut adalah diagram Hasse untuk (S, R):
[Gambar Diagram Hasse untuk (S, R)]
Dalam diagram Hasse, kita dapat melihat bahwa:
- Elemen 6 berada di bagian atas diagram karena tidak ditutupi oleh elemen lain.
- Elemen 1, 2, 3, 4, dan 5 berada di bagian bawah diagram karena tidak menutupi elemen lain.
- Elemen 2 dan 3 menutupi elemen 6.
- Elemen 1 dan 4 menutupi elemen 2.
- Elemen 5 menutupi elemen 1.
Elemen Minimal, Elemen Maksimal, Elemen Terbesar, dan Elemen Terkecil dari (S, R)
Berikut adalah penjelasan untuk masing-masing elemen:
- Elemen minimal adalah elemen yang tidak ditutupi oleh elemen lain. Dalam (S, R), elemen minimal adalah 1, 2, 3, 4, dan 5.
- Elemen maksimal adalah elemen yang tidak menutupi elemen lain. Dalam (S, R), elemen maksimal adalah 6.
- Elemen terbesar adalah elemen yang menutupi semua elemen lain. Dalam (S, R), elemen terbesar adalah 6.
- Elemen terkecil adalah elemen yang ditutupi oleh semua elemen lain. Dalam (S, R), tidak ada elemen terkecil.
Rantai dan Antirantai Terpanjang dari (S, R)
Berikut adalah penjelasan untuk masing-masing:
- Rantai adalah himpunan bagian dari S yang terurut total. Dalam (S, R), rantai terpanjang adalah 1, 2, 6 atau 1, 4, 6 atau 5, 1, 2, 6 atau 5, 1, 4, 6. Panjang rantai terpanjang adalah 3.
- Antirantai adalah himpunan bagian dari S yang tidak memiliki dua elemen yang saling berhubungan. Dalam (S, R), antirantai terpanjang adalah 1, 3, 4, 5 atau 2, 3, 4, 5. Panjang antirantai terpanjang adalah 4.
Akhir Kata
Memahami poset membuka pintu menuju pemahaman yang lebih dalam tentang relasi dan struktur matematika. Dengan contoh soal yang beragam, kita dapat melatih kemampuan berpikir logis dan memecahkan masalah dengan menggunakan konsep poset.






