Contoh soal program linear – Pernahkah kamu berpikir bagaimana toko kelontong menentukan jumlah barang yang harus dipesan agar keuntungan maksimal? Atau bagaimana pabrik menentukan jumlah produksi untuk memenuhi permintaan pasar? Program linear adalah alat yang ampuh untuk menyelesaikan masalah optimasi seperti ini. Program linear adalah metode matematika yang digunakan untuk menentukan solusi terbaik dari suatu masalah dengan batasan tertentu. Dalam kehidupan sehari-hari, program linear dapat diterapkan dalam berbagai bidang seperti ekonomi, produksi, logistik, dan bahkan kesehatan.
Di sini, kita akan menjelajahi contoh soal program linear yang menarik dan bagaimana cara menyelesaikannya dengan berbagai metode. Kamu akan belajar bagaimana merumuskan model matematika, menggunakan metode grafik dan simplex, serta memahami interpretasi solusi optimal. Siap untuk menyelami dunia program linear? Mari kita mulai!
Metode Penyelesaian Program Linear
Program linear merupakan model matematika yang digunakan untuk menyelesaikan masalah optimasi dengan batasan-batasan tertentu. Untuk mendapatkan solusi optimal, terdapat beberapa metode yang dapat digunakan, salah satunya adalah metode grafik.
Metode Grafik
Metode grafik adalah metode penyelesaian program linear dengan cara menggambarkan batasan-batasan dan fungsi objektif pada bidang Cartesius. Dengan menggambar grafik, kita dapat menentukan daerah penyelesaian dan titik-titik ekstrem yang merupakan calon solusi optimal.
Langkah-langkah Metode Grafik
Berikut adalah langkah-langkah yang dapat digunakan untuk menyelesaikan program linear dengan metode grafik:
- Tentukan fungsi objektif dan batasan-batasan dari masalah program linear.
- Ubah setiap batasan menjadi persamaan garis.
- Gambar garis-garis yang mewakili batasan-batasan pada bidang Cartesius.
- Tentukan daerah penyelesaian yang memenuhi semua batasan.
- Tentukan titik-titik ekstrem dari daerah penyelesaian.
- Evaluasi fungsi objektif pada setiap titik ekstrem.
- Tentukan titik ekstrem yang memberikan nilai optimal (maksimum atau minimum) pada fungsi objektif.
Contoh Soal
Misalkan sebuah perusahaan memproduksi dua jenis produk, yaitu produk A dan produk B. Setiap produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku, sedangkan setiap produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku. Perusahaan memiliki ketersediaan 10 jam waktu produksi dan 8 kg bahan baku. Keuntungan yang diperoleh dari penjualan setiap produk A adalah Rp10.000,- dan setiap produk B adalah Rp15.000,-. Berapakah jumlah produk A dan produk B yang harus diproduksi untuk mendapatkan keuntungan maksimum?
Solusi
Berikut adalah langkah-langkah penyelesaian program linear dengan metode grafik untuk contoh soal di atas:
- Tentukan fungsi objektif dan batasan-batasan
- Fungsi objektif: Keuntungan (Z) = 10.000A + 15.000B
- Batasan-batasan:
- Waktu produksi: 2A + B ≤ 10
- Bahan baku: A + 2B ≤ 8
- A ≥ 0, B ≥ 0 (Jumlah produk tidak boleh negatif)
- Ubah setiap batasan menjadi persamaan garis
- 2A + B = 10
- A + 2B = 8
- Gambar garis-garis yang mewakili batasan-batasan pada bidang Cartesius
Untuk menggambar garis, kita dapat menentukan dua titik pada garis tersebut. Misalnya, untuk garis 2A + B = 10, kita dapat mengambil titik (0, 10) dan (5, 0). Kemudian, hubungkan kedua titik tersebut dengan garis lurus. Lakukan hal yang sama untuk garis A + 2B = 8.
- Tentukan daerah penyelesaian yang memenuhi semua batasan
Daerah penyelesaian adalah daerah yang memenuhi semua batasan. Untuk menentukan daerah penyelesaian, kita dapat mengambil titik uji pada setiap sisi garis. Misalnya, untuk garis 2A + B = 10, kita dapat mengambil titik uji (0, 0). Substitusikan titik uji ke dalam persamaan batasan. Jika hasil substitusi memenuhi persamaan batasan, maka daerah yang mengandung titik uji adalah daerah penyelesaian. Lakukan hal yang sama untuk semua batasan.
- Tentukan titik-titik ekstrem dari daerah penyelesaian
Titik-titik ekstrem adalah titik-titik yang terletak pada perpotongan garis-garis batasan. Pada contoh soal ini, terdapat empat titik ekstrem, yaitu (0, 0), (0, 4), (4, 2), dan (5, 0).
- Evaluasi fungsi objektif pada setiap titik ekstrem
- Z(0, 0) = 10.000(0) + 15.000(0) = 0
- Z(0, 4) = 10.000(0) + 15.000(4) = 60.000
- Z(4, 2) = 10.000(4) + 15.000(2) = 70.000
- Z(5, 0) = 10.000(5) + 15.000(0) = 50.000
- Tentukan titik ekstrem yang memberikan nilai optimal (maksimum atau minimum) pada fungsi objektif
Dari hasil evaluasi fungsi objektif, diperoleh bahwa titik ekstrem (4, 2) memberikan nilai keuntungan maksimum, yaitu Rp70.000,-. Oleh karena itu, perusahaan harus memproduksi 4 produk A dan 2 produk B untuk mendapatkan keuntungan maksimum.
Tabel Solusi Optimal
| Titik Ekstrem | Keuntungan (Z) |
|---|---|
| (0, 0) | 0 |
| (0, 4) | 60.000 |
| (4, 2) | 70.000 |
| (5, 0) | 50.000 |
Dari tabel di atas, dapat dilihat bahwa titik ekstrem (4, 2) memberikan nilai keuntungan maksimum, yaitu Rp70.000,-.
Contoh soal program linear seringkali melibatkan masalah optimasi, seperti menentukan jumlah produksi maksimum dengan keterbatasan sumber daya. Nah, mirip dengan itu, kamu bisa menemukan contoh soal kasus neonatus dan jawabannya di sini , yang mengkaji tentang optimalisasi penanganan bayi baru lahir.
Misalnya, menentukan jumlah susu formula terbaik untuk bayi prematur dengan mempertimbangkan berat badan dan kebutuhan nutrisi. Dengan mempelajari soal-soal seperti ini, kamu bisa lebih memahami konsep program linear dalam berbagai konteks.
Metode Simplex
Metode Simplex adalah algoritma yang digunakan untuk menyelesaikan masalah program linear. Algoritma ini bekerja dengan iterasi, dengan setiap iterasi menguji solusi yang layak dan bergerak ke solusi yang lebih baik sampai solusi optimal ditemukan. Metode Simplex sangat berguna dalam berbagai bidang, seperti ekonomi, teknik, dan ilmu komputer.
Penjelasan Metode Simplex
Metode Simplex bekerja dengan membangun solusi dasar yang layak dan kemudian secara berulang-ulang meningkatkan solusi tersebut sampai solusi optimal ditemukan. Solusi dasar yang layak adalah solusi yang memenuhi semua kendala dan semua variabel non-negatif. Setiap iterasi melibatkan pemilihan variabel masuk dan variabel keluar, yang diubah untuk meningkatkan nilai fungsi objektif. Proses ini berlanjut sampai tidak ada lagi variabel masuk yang dapat meningkatkan nilai fungsi objektif, yang menunjukkan bahwa solusi optimal telah ditemukan.
Contoh Soal Program Linear dan Solusi Metode Simplex
Sebuah perusahaan memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 jam waktu perakitan, sedangkan produk B membutuhkan 1 jam waktu produksi dan 2 jam waktu perakitan. Perusahaan memiliki 10 jam waktu produksi dan 8 jam waktu perakitan yang tersedia. Keuntungan dari produk A adalah Rp10.000 per unit, dan keuntungan dari produk B adalah Rp15.000 per unit. Berapa banyak unit produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan?
Langkah-langkah Penyelesaian dengan Metode Simplex:
1. Membuat Model Matematika:
– Variabel keputusan:
– x = jumlah unit produk A yang diproduksi
– y = jumlah unit produk B yang diproduksi
– Fungsi objektif:
– Z = 10000x + 15000y (memaksimalkan keuntungan)
– Kendala:
– 2x + y ≤ 10 (kendala waktu produksi)
– x + 2y ≤ 8 (kendala waktu perakitan)
– x ≥ 0, y ≥ 0 (kendala non-negatif)
2. Menyusun Tabel Simplex:
– Tabel Simplex berisi koefisien dari variabel keputusan, kendala, dan fungsi objektif.
– Tabel Simplex awal:
| Variabel | x | y | S1 | S2 | Z | RHS |
|—|—|—|—|—|—|—|
| S1 | 2 | 1 | 1 | 0 | 0 | 10 |
| S2 | 1 | 2 | 0 | 1 | 0 | 8 |
| Z | -10000 | -15000 | 0 | 0 | 1 | 0 |
– S1 dan S2 adalah variabel slack, yang digunakan untuk mengubah kendala menjadi persamaan.
– RHS adalah sisi kanan dari persamaan kendala.
3. Memilih Variabel Masuk:
– Variabel masuk adalah variabel yang memiliki koefisien negatif terbesar dalam baris Z.
– Dalam tabel ini, variabel masuk adalah y karena memiliki koefisien -15000.
4. Memilih Variabel Keluar:
– Variabel keluar adalah variabel yang memiliki rasio terkecil antara RHS dan koefisien variabel masuk dalam kolom yang sama.
– Dalam tabel ini, variabel keluar adalah S2 karena memiliki rasio 8/2 = 4.
5. Membuat Pivot:
– Pivot adalah elemen yang berada pada persimpangan baris variabel keluar dan kolom variabel masuk.
– Dalam tabel ini, pivot adalah 2.
6. Melakukan Operasi Baris:
– Lakukan operasi baris untuk mengubah pivot menjadi 1 dan mengubah elemen lain dalam kolom variabel masuk menjadi 0.
– Tabel Simplex setelah operasi baris:
| Variabel | x | y | S1 | S2 | Z | RHS |
|—|—|—|—|—|—|—|
| S1 | 3/2 | 0 | 1 | -1/2 | 0 | 6 |
| y | 1/2 | 1 | 0 | 1/2 | 0 | 4 |
| Z | -5000 | 0 | 0 | 7500 | 1 | 60000 |
7. Ulangi Langkah 3-6:
– Ulangi langkah 3-6 sampai semua koefisien dalam baris Z tidak negatif.
– Dalam tabel ini, variabel masuk adalah x karena memiliki koefisien -5000.
– Variabel keluar adalah S1 karena memiliki rasio 6/(3/2) = 4.
– Pivot adalah 3/2.
– Setelah operasi baris, tabel Simplex menjadi:
| Variabel | x | y | S1 | S2 | Z | RHS |
|—|—|—|—|—|—|—|
| x | 1 | 0 | 2/3 | -1/3 | 0 | 4 |
| y | 0 | 1 | -1/3 | 2/3 | 0 | 2 |
| Z | 0 | 0 | 10000/3 | 5000/3 | 1 | 80000 |
8. Solusi Optimal:
– Solusi optimal telah ditemukan karena semua koefisien dalam baris Z tidak negatif.
– Solusi optimal adalah x = 4, y = 2, dan Z = 80000.
– Ini berarti perusahaan harus memproduksi 4 unit produk A dan 2 unit produk B untuk memaksimalkan keuntungan sebesar Rp80.000.
Tabel Langkah-langkah Metode Simplex
| Langkah | Deskripsi |
|—|—|
| 1 | Membuat Model Matematika |
| 2 | Menyusun Tabel Simplex |
| 3 | Memilih Variabel Masuk |
| 4 | Memilih Variabel Keluar |
| 5 | Membuat Pivot |
| 6 | Melakukan Operasi Baris |
| 7 | Ulangi Langkah 3-6 sampai semua koefisien dalam baris Z tidak negatif |
| 8 | Solusi Optimal |
Penerapan Program Linear
Program linear merupakan alat yang ampuh dalam menyelesaikan masalah optimasi, khususnya dalam konteks bisnis dan ekonomi. Prinsipnya sederhana: memaksimalkan keuntungan atau meminimalkan biaya dengan memanfaatkan sumber daya yang terbatas. Penerapan program linear dapat dijumpai di berbagai bidang, mulai dari produksi dan keuangan hingga transportasi dan manajemen persediaan.
Penerapan Program Linear dalam Bidang Ekonomi
Program linear banyak digunakan dalam bidang ekonomi untuk membantu perusahaan dalam pengambilan keputusan strategis. Misalnya, dalam menentukan strategi produksi yang optimal, program linear dapat digunakan untuk menentukan jumlah produk yang harus diproduksi untuk memaksimalkan keuntungan, dengan mempertimbangkan keterbatasan sumber daya seperti tenaga kerja, bahan baku, dan modal.
Strategi Produksi Optimal dengan Program Linear
Program linear dapat membantu perusahaan dalam menentukan strategi produksi yang optimal dengan memaksimalkan keuntungan atau meminimalkan biaya produksi. Caranya adalah dengan merumuskan masalah produksi sebagai model matematika yang terdiri dari fungsi objektif (menyatakan tujuan yang ingin dicapai, seperti memaksimalkan keuntungan) dan batasan (menyatakan keterbatasan sumber daya, seperti ketersediaan bahan baku, tenaga kerja, dan modal).
Sebagai contoh, sebuah perusahaan manufaktur memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku, sedangkan produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku. Perusahaan memiliki 100 jam waktu produksi dan 80 kg bahan baku yang tersedia. Keuntungan dari setiap produk A adalah Rp10.000, sedangkan produk B adalah Rp15.000.
Dengan menggunakan program linear, perusahaan dapat menentukan jumlah produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan. Fungsi objektif dalam kasus ini adalah memaksimalkan keuntungan (Rp10.000A + Rp15.000B), dengan batasan waktu produksi (2A + B ≤ 100) dan ketersediaan bahan baku (A + 2B ≤ 80).
Contoh Penerapan Program Linear dalam Berbagai Bidang, Contoh soal program linear
| Bidang | Contoh Penerapan Program Linear |
|---|---|
| Produksi | Menentukan jumlah produk yang harus diproduksi untuk memaksimalkan keuntungan, dengan mempertimbangkan keterbatasan sumber daya seperti tenaga kerja, bahan baku, dan modal. |
| Keuangan | Membuat portofolio investasi yang optimal, dengan mempertimbangkan tingkat pengembalian dan risiko yang diinginkan. |
| Transportasi | Menentukan rute pengiriman yang optimal untuk meminimalkan biaya transportasi. |
| Manajemen Persediaan | Menentukan jumlah persediaan yang optimal untuk meminimalkan biaya penyimpanan dan kekurangan persediaan. |
| Pemasaran | Menentukan strategi pemasaran yang optimal untuk memaksimalkan penjualan, dengan mempertimbangkan anggaran pemasaran dan segmentasi pasar. |
Contoh Soal Program Linear
Program linear merupakan metode matematika yang digunakan untuk menyelesaikan masalah optimasi dengan batasan tertentu. Masalah ini dapat diubah ke dalam bentuk model matematika yang terdiri dari fungsi objektif dan kendala. Model matematika tersebut kemudian dapat diselesaikan dengan berbagai metode, seperti metode grafik, metode simplex, atau metode lainnya. Berikut ini adalah beberapa contoh soal program linear yang dapat membantu Anda memahami konsep program linear.
Contoh Soal Pemahaman Model Matematika
Contoh soal ini dirancang untuk menguji pemahaman Anda dalam merumuskan model matematika dari masalah program linear. Anda perlu menentukan fungsi objektif dan kendala berdasarkan informasi yang diberikan.
- Sebuah perusahaan memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku per unit, sedangkan produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku per unit. Perusahaan memiliki 100 jam waktu produksi dan 60 kg bahan baku tersedia. Keuntungan per unit produk A adalah Rp. 10.000 dan per unit produk B adalah Rp. 15.000. Berapakah jumlah masing-masing produk yang harus diproduksi untuk memaksimalkan keuntungan?
- Seorang petani ingin menanam dua jenis tanaman, X dan Y. Tanaman X membutuhkan 10 kg pupuk dan 5 liter air per hektar, sedangkan tanaman Y membutuhkan 5 kg pupuk dan 10 liter air per hektar. Petani memiliki 100 kg pupuk dan 50 liter air tersedia. Keuntungan per hektar tanaman X adalah Rp. 1.000.000 dan per hektar tanaman Y adalah Rp. 1.500.000. Berapakah luas lahan yang harus ditanami masing-masing tanaman untuk memaksimalkan keuntungan?
- Sebuah perusahaan memiliki dua jenis mesin, A dan B. Mesin A dapat memproduksi 100 unit produk per jam, sedangkan mesin B dapat memproduksi 150 unit produk per jam. Perusahaan membutuhkan minimal 1.000 unit produk per hari. Biaya operasional mesin A adalah Rp. 500.000 per jam, sedangkan biaya operasional mesin B adalah Rp. 750.000 per jam. Berapakah waktu operasional masing-masing mesin untuk meminimalkan biaya operasional?
Contoh Soal Metode Grafik
Contoh soal ini dirancang untuk dilatih dengan metode grafik. Metode grafik adalah metode visual yang digunakan untuk menyelesaikan masalah program linear dengan menggambar garis yang mewakili kendala dan mencari titik optimum yang berada di dalam area yang memenuhi semua kendala.
- Sebuah perusahaan memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku per unit, sedangkan produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku per unit. Perusahaan memiliki 100 jam waktu produksi dan 60 kg bahan baku tersedia. Keuntungan per unit produk A adalah Rp. 10.000 dan per unit produk B adalah Rp. 15.000. Berapakah jumlah masing-masing produk yang harus diproduksi untuk memaksimalkan keuntungan? (Gunakan metode grafik untuk menyelesaikan masalah ini)
- Seorang petani ingin menanam dua jenis tanaman, X dan Y. Tanaman X membutuhkan 10 kg pupuk dan 5 liter air per hektar, sedangkan tanaman Y membutuhkan 5 kg pupuk dan 10 liter air per hektar. Petani memiliki 100 kg pupuk dan 50 liter air tersedia. Keuntungan per hektar tanaman X adalah Rp. 1.000.000 dan per hektar tanaman Y adalah Rp. 1.500.000. Berapakah luas lahan yang harus ditanami masing-masing tanaman untuk memaksimalkan keuntungan? (Gunakan metode grafik untuk menyelesaikan masalah ini)
Contoh Soal Metode Simplex
Contoh soal ini dirancang untuk dilatih dengan metode simplex. Metode simplex adalah metode aljabar yang digunakan untuk menyelesaikan masalah program linear dengan menggunakan tabel simplex. Metode ini lebih kompleks dibandingkan dengan metode grafik, tetapi dapat digunakan untuk menyelesaikan masalah dengan lebih banyak variabel dan kendala.
- Sebuah perusahaan memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku per unit, sedangkan produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku per unit. Perusahaan memiliki 100 jam waktu produksi dan 60 kg bahan baku tersedia. Keuntungan per unit produk A adalah Rp. 10.000 dan per unit produk B adalah Rp. 15.000. Berapakah jumlah masing-masing produk yang harus diproduksi untuk memaksimalkan keuntungan? (Gunakan metode simplex untuk menyelesaikan masalah ini)
Aplikasi Program Linear
Program linear merupakan alat yang ampuh dalam menyelesaikan masalah optimasi, yaitu menemukan solusi terbaik yang memenuhi batasan tertentu. Program linear dapat diterapkan dalam berbagai bidang, mulai dari bisnis hingga ilmu pengetahuan.
Pengalokasian Sumber Daya
Program linear sangat berguna dalam pengalokasian sumber daya yang terbatas untuk mencapai tujuan tertentu. Misalnya, perusahaan manufaktur dapat menggunakan program linear untuk menentukan jumlah optimal produk yang harus diproduksi untuk memaksimalkan keuntungan, dengan mempertimbangkan keterbatasan bahan baku, tenaga kerja, dan waktu produksi.
Perencanaan Produksi
Program linear juga dapat digunakan untuk merencanakan produksi secara optimal. Misalnya, perusahaan dapat menggunakan program linear untuk menentukan jumlah produk yang harus diproduksi di setiap pabrik, dengan mempertimbangkan biaya produksi, kapasitas pabrik, dan permintaan pasar.
Optimasi Portofolio
Dalam dunia keuangan, program linear dapat digunakan untuk mengoptimalkan portofolio investasi. Misalnya, investor dapat menggunakan program linear untuk menentukan proporsi optimal dari setiap aset dalam portofolio, dengan mempertimbangkan tingkat pengembalian yang diharapkan, risiko, dan batasan investasi.
Aplikasi Program Linear dalam Bidang Lain
Program linear memiliki aplikasi yang luas di berbagai bidang lain, seperti:
- Logistik: Program linear dapat digunakan untuk menentukan rute pengiriman yang optimal untuk meminimalkan biaya transportasi.
- Kesehatan: Program linear dapat digunakan untuk merencanakan alokasi sumber daya medis, seperti tempat tidur rumah sakit, staf medis, dan peralatan medis, untuk memaksimalkan efisiensi dan efektivitas layanan kesehatan.
- Lingkungan: Program linear dapat digunakan untuk mengoptimalkan penggunaan sumber daya alam, seperti air dan energi, untuk meminimalkan dampak lingkungan.
Contoh Aplikasi Program Linear
Berikut adalah tabel yang menunjukkan berbagai aplikasi program linear beserta contoh kasusnya:
| Aplikasi | Contoh Kasus |
|---|---|
| Pengalokasian Sumber Daya | Sebuah perusahaan manufaktur memiliki dua jenis mesin, A dan B, yang dapat digunakan untuk memproduksi dua jenis produk, X dan Y. Setiap mesin memiliki kapasitas produksi yang berbeda untuk setiap produk. Perusahaan ingin menentukan jumlah optimal produk X dan Y yang harus diproduksi untuk memaksimalkan keuntungan, dengan mempertimbangkan keterbatasan kapasitas mesin. |
| Perencanaan Produksi | Sebuah perusahaan makanan memiliki tiga pabrik yang memproduksi produk yang sama. Setiap pabrik memiliki biaya produksi yang berbeda dan kapasitas produksi yang berbeda. Perusahaan ingin menentukan jumlah produk yang harus diproduksi di setiap pabrik untuk meminimalkan biaya produksi total, dengan mempertimbangkan permintaan pasar. |
| Optimasi Portofolio | Seorang investor ingin menginvestasikan uangnya dalam tiga jenis aset: saham, obligasi, dan properti. Setiap aset memiliki tingkat pengembalian yang diharapkan yang berbeda dan risiko yang berbeda. Investor ingin menentukan proporsi optimal dari setiap aset dalam portofolio untuk memaksimalkan pengembalian, dengan mempertimbangkan tingkat risiko yang dapat diterima. |
| Logistik | Sebuah perusahaan pengiriman memiliki beberapa gudang dan beberapa titik pengiriman. Perusahaan ingin menentukan rute pengiriman yang optimal untuk meminimalkan biaya transportasi, dengan mempertimbangkan jarak antara gudang dan titik pengiriman, kapasitas truk, dan waktu pengiriman. |
| Kesehatan | Sebuah rumah sakit memiliki sejumlah tempat tidur yang terbatas dan sejumlah staf medis yang terbatas. Rumah sakit ingin menentukan jumlah pasien yang harus dirawat di setiap departemen, dengan mempertimbangkan kebutuhan perawatan pasien, kapasitas tempat tidur, dan ketersediaan staf medis. |
| Lingkungan | Sebuah perusahaan energi ingin meminimalkan emisi gas rumah kaca dari pembangkit listriknya. Perusahaan memiliki beberapa pilihan teknologi pembangkit listrik yang memiliki emisi gas rumah kaca yang berbeda dan biaya produksi yang berbeda. Perusahaan ingin menentukan kombinasi teknologi yang optimal untuk meminimalkan emisi gas rumah kaca, dengan mempertimbangkan biaya produksi. |
Keuntungan dan Kerugian Program Linear
Program linear merupakan metode yang digunakan untuk menyelesaikan masalah optimasi, yaitu mencari solusi terbaik dari suatu masalah dengan batasan-batasan tertentu. Metode ini sangat berguna dalam berbagai bidang, seperti ekonomi, bisnis, dan teknik. Program linear dapat digunakan untuk memaksimalkan keuntungan, meminimalkan biaya, atau mencari solusi optimal untuk masalah logistik dan produksi. Namun, seperti metode lainnya, program linear juga memiliki keuntungan dan kerugian yang perlu dipertimbangkan.
Keuntungan Program Linear
Program linear memiliki beberapa keuntungan yang membuatnya menjadi metode yang efektif untuk menyelesaikan masalah optimasi. Keuntungan tersebut meliputi:
- Metode yang sistematis dan terstruktur: Program linear memberikan pendekatan yang terstruktur untuk menyelesaikan masalah optimasi. Metode ini menggunakan model matematika untuk merepresentasikan masalah dan memberikan solusi yang optimal berdasarkan batasan yang ada.
- Dapat menyelesaikan masalah kompleks: Program linear dapat digunakan untuk menyelesaikan masalah yang kompleks dengan banyak variabel dan batasan. Hal ini memungkinkan pengambilan keputusan yang lebih baik dengan mempertimbangkan semua faktor yang relevan.
- Memberikan solusi optimal: Program linear menjamin solusi optimal untuk masalah yang diberikan. Solusi ini merupakan solusi terbaik yang dapat dicapai dengan batasan yang ada.
- Mudah dipahami dan diimplementasikan: Program linear merupakan metode yang relatif mudah dipahami dan diimplementasikan, terutama dengan bantuan perangkat lunak komputer.
- Dapat digunakan dalam berbagai bidang: Program linear memiliki aplikasi yang luas di berbagai bidang, seperti ekonomi, bisnis, teknik, dan ilmu komputer.
Kelemahan Program Linear
Meskipun memiliki banyak keuntungan, program linear juga memiliki beberapa kelemahan yang perlu dipertimbangkan. Kelemahan tersebut meliputi:
- Asumsi linearitas: Program linear mengasumsikan bahwa hubungan antara variabel dalam model adalah linear. Asumsi ini mungkin tidak selalu berlaku dalam dunia nyata, yang dapat menyebabkan solusi yang tidak akurat.
- Batasan pada jumlah variabel dan batasan: Program linear dapat menjadi rumit untuk diimplementasikan ketika jumlah variabel dan batasan meningkat. Hal ini dapat menyebabkan waktu komputasi yang lama dan kesulitan dalam menemukan solusi.
- Tidak dapat menangani masalah non-linear: Program linear tidak dapat menangani masalah optimasi yang melibatkan hubungan non-linear antara variabel.
- Membutuhkan data yang akurat: Program linear membutuhkan data yang akurat untuk menghasilkan solusi yang akurat. Kesalahan dalam data dapat menyebabkan solusi yang tidak valid.
- Tidak selalu realistis: Model program linear terkadang tidak realistis karena mengabaikan faktor-faktor penting yang tidak dapat diukur atau dimodelkan.
Perbandingan Keuntungan dan Kerugian Program Linear
Berikut adalah tabel yang menunjukkan perbandingan keuntungan dan kerugian program linear:
| Aspek | Keuntungan | Kerugian |
|---|---|---|
| Metode | Sistematis dan terstruktur | Asumsi linearitas |
| Kompleksitas | Dapat menyelesaikan masalah kompleks | Batasan pada jumlah variabel dan batasan |
| Solusi | Memberikan solusi optimal | Tidak dapat menangani masalah non-linear |
| Implementasi | Mudah dipahami dan diimplementasikan | Membutuhkan data yang akurat |
| Aplikasi | Dapat digunakan dalam berbagai bidang | Tidak selalu realistis |
Perkembangan Program Linear
Program linear adalah salah satu cabang ilmu matematika yang membahas tentang optimasi suatu fungsi linear dengan batasan berupa persamaan atau pertidaksamaan linear. Program linear memiliki peran penting dalam berbagai bidang, seperti ekonomi, bisnis, industri, dan ilmu komputer.
Perkembangan Program Linear dari Masa ke Masa
Program linear telah mengalami perkembangan yang signifikan sejak pertama kali diperkenalkan.
- Awal Mula: Program linear pertama kali diperkenalkan pada tahun 1940-an oleh George B. Dantzig. Metode Simplex, yang ditemukan oleh Dantzig, menjadi metode standar untuk menyelesaikan masalah program linear.
- Perkembangan Komputer: Dengan munculnya komputer pada tahun 1950-an, kemampuan untuk menyelesaikan masalah program linear yang lebih kompleks meningkat pesat. Perkembangan komputer memungkinkan pengembangan algoritma yang lebih canggih dan efisien.
- Peningkatan Metode: Seiring waktu, metode baru untuk menyelesaikan masalah program linear terus dikembangkan. Metode seperti metode interior-point dan metode branch-and-bound telah memberikan solusi yang lebih cepat dan efisien untuk masalah yang lebih besar.
- Aplikasi yang Luas: Program linear telah diaplikasikan secara luas dalam berbagai bidang. Contohnya, dalam ekonomi, program linear digunakan untuk menentukan strategi produksi yang optimal. Dalam bisnis, program linear digunakan untuk memaksimalkan keuntungan dan meminimalkan biaya. Dalam industri, program linear digunakan untuk merancang sistem produksi yang efisien.
Software dan Tools untuk Menyelesaikan Program Linear
Ada berbagai software dan tools yang dapat digunakan untuk menyelesaikan masalah program linear. Beberapa software yang populer meliputi:
- Excel Solver: Excel Solver adalah add-in yang tersedia di Microsoft Excel yang dapat digunakan untuk menyelesaikan masalah program linear. Solver menggunakan algoritma Simplex untuk menemukan solusi optimal.
- Gurobi Optimizer: Gurobi Optimizer adalah software komersial yang dirancang khusus untuk menyelesaikan masalah program linear dan masalah optimasi lainnya. Gurobi Optimizer memiliki kemampuan untuk menangani masalah yang sangat besar dan kompleks.
- CPLEX Optimizer: CPLEX Optimizer adalah software komersial lainnya yang menawarkan kemampuan untuk menyelesaikan masalah program linear dan masalah optimasi lainnya. CPLEX Optimizer dikenal karena kecepatan dan efisiensi algoritmanya.
- SCIP: SCIP adalah software open-source yang dapat digunakan untuk menyelesaikan masalah program linear, integer, dan masalah optimasi lainnya. SCIP dikenal karena kemampuannya untuk menangani masalah yang kompleks dan kemampuannya untuk menghasilkan solusi yang berkualitas tinggi.
Contoh Kasus Program Linear yang Kompleks
Misalnya, sebuah perusahaan manufaktur ingin menentukan jumlah produk yang harus diproduksi untuk memaksimalkan keuntungan. Perusahaan ini memiliki berbagai batasan, seperti ketersediaan bahan baku, kapasitas produksi, dan permintaan pasar. Untuk menentukan solusi optimal, perusahaan ini dapat menggunakan program linear.
Masalah ini dapat dimodelkan dengan menggunakan program linear dengan fungsi objektif yang memaksimalkan keuntungan dan batasan yang mewakili ketersediaan bahan baku, kapasitas produksi, dan permintaan pasar. Untuk menyelesaikan masalah ini, perusahaan dapat menggunakan software program linear seperti Gurobi Optimizer atau CPLEX Optimizer. Software ini dapat membantu perusahaan untuk menentukan solusi optimal yang memaksimalkan keuntungan dengan mempertimbangkan semua batasan yang ada.
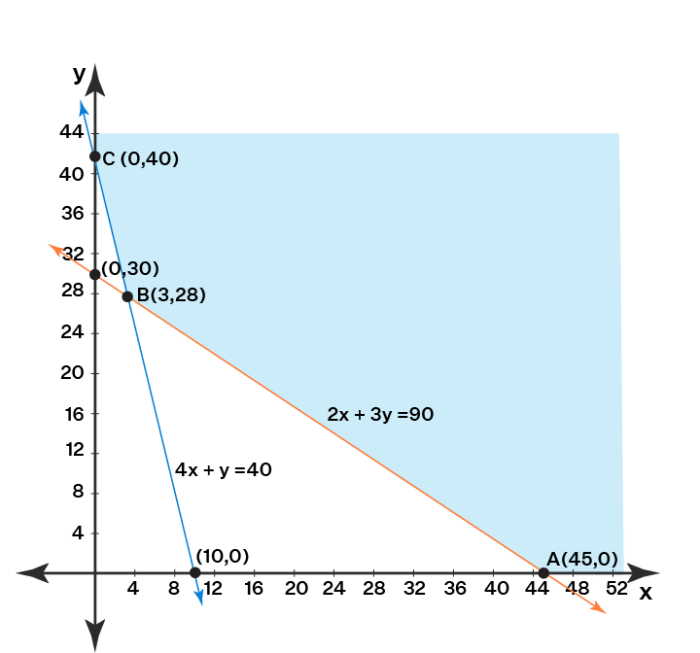
Contoh Soal Program Linear dengan Ilustrasi
Program linear merupakan alat yang ampuh dalam menyelesaikan masalah optimasi, terutama dalam konteks pembatasan sumber daya. Dengan menggunakan model matematika, program linear memungkinkan kita untuk menentukan strategi terbaik untuk mencapai tujuan tertentu, sembari tetap memperhatikan batasan yang ada.
Contoh Soal Program Linear
Misalnya, sebuah perusahaan ingin memproduksi dua jenis produk, yaitu produk A dan produk B. Setiap produk membutuhkan bahan baku dan waktu produksi yang berbeda. Berikut adalah tabel yang merangkum informasi terkait:
| Produk | Bahan Baku (kg) | Waktu Produksi (jam) | Keuntungan (Rp) |
|---|---|---|---|
| A | 2 | 3 | 100.000 |
| B | 3 | 2 | 150.000 |
Perusahaan memiliki keterbatasan sumber daya, yaitu 12 kg bahan baku dan 15 jam waktu produksi. Tujuan perusahaan adalah memaksimalkan keuntungan. Bagaimana perusahaan dapat menentukan jumlah produksi optimal untuk setiap produk?
Ilustrasi Visual
Untuk menggambarkan model matematika program linear, kita dapat menggunakan grafik. Sumbu horizontal mewakili jumlah produk A, dan sumbu vertikal mewakili jumlah produk B.
Interpretasi Solusi Optimal
Solusi optimal dari program linear tersebut adalah titik yang terletak di dalam daerah layak yang memaksimalkan fungsi objektif (keuntungan). Titik ini dapat ditemukan dengan menguji titik-titik sudut dari daerah layak.
Kesimpulan
Program linear merupakan alat yang powerful dalam pengambilan keputusan yang melibatkan optimasi dan batasan sumber daya. Dengan memahami konsep dasar program linear dan cara mengimplementasikannya, perusahaan dapat membuat keputusan yang lebih baik dan meningkatkan efisiensi operasi.
Terakhir
Dengan memahami konsep program linear, kamu dapat menemukan solusi terbaik untuk berbagai masalah optimasi. Mulai dari menentukan strategi produksi yang optimal hingga mengalokasikan sumber daya secara efisien, program linear dapat membantu kita membuat keputusan yang lebih baik. Menguasai program linear bukan hanya tentang menyelesaikan soal matematika, tetapi juga tentang mengembangkan kemampuan berpikir analitis dan memecahkan masalah secara sistematis.