Contoh soal riset operasi – Riset operasi, sebuah bidang ilmu yang memfokuskan diri pada penerapan metode matematis dan statistik untuk memecahkan masalah kompleks, hadir sebagai solusi cerdas untuk berbagai tantangan di dunia nyata. Dari mengoptimalkan jalur pengiriman hingga menentukan strategi produksi yang efisien, riset operasi menawarkan pendekatan sistematis untuk menemukan solusi terbaik.
Dalam artikel ini, kita akan menjelajahi contoh-contoh soal riset operasi yang umum ditemui, mulai dari masalah transportasi hingga pengambilan keputusan. Dengan memahami dasar-dasar riset operasi, Anda akan mampu mengaplikasikan konsep optimasi dalam berbagai bidang, mulai dari bisnis hingga kehidupan sehari-hari.
Pengertian Riset Operasi
Riset operasi adalah disiplin ilmu yang menggunakan metode ilmiah untuk memecahkan masalah kompleks yang dihadapi oleh organisasi atau individu. Riset operasi menggunakan pendekatan sistematis untuk mengidentifikasi masalah, mengembangkan model matematis, menganalisis data, dan mencari solusi optimal.
Aplikasi Riset Operasi dalam Kehidupan Sehari-hari
Riset operasi memiliki banyak aplikasi dalam kehidupan sehari-hari. Contohnya, riset operasi digunakan untuk:
- Merencanakan rute pengiriman barang agar lebih efisien.
- Menentukan jadwal penerbangan agar optimal.
- Membuat strategi investasi yang menguntungkan.
- Mengatur alur lalu lintas di jalan raya untuk mengurangi kemacetan.
Perbedaan Riset Operasi dengan Ilmu Lain
Riset operasi berbeda dengan ilmu lain yang terkait, seperti statistika dan ilmu komputer. Berikut tabel yang menunjukkan perbedaannya:
| Aspek | Riset Operasi | Statistika | Ilmu Komputer |
|---|---|---|---|
| Fokus | Memecahkan masalah kompleks dengan pendekatan sistematis | Menganalisis data dan menarik kesimpulan | Mengembangkan algoritma dan sistem komputer |
| Metode | Model matematis, simulasi, optimasi | Analisis data, uji hipotesis, probabilitas | Pemrograman, algoritma, struktur data |
| Aplikasi | Manajemen, logistik, keuangan, kesehatan | Ilmu sosial, ekonomi, biologi, kedokteran | Teknologi informasi, rekayasa perangkat lunak, robotika |
Metode Riset Operasi
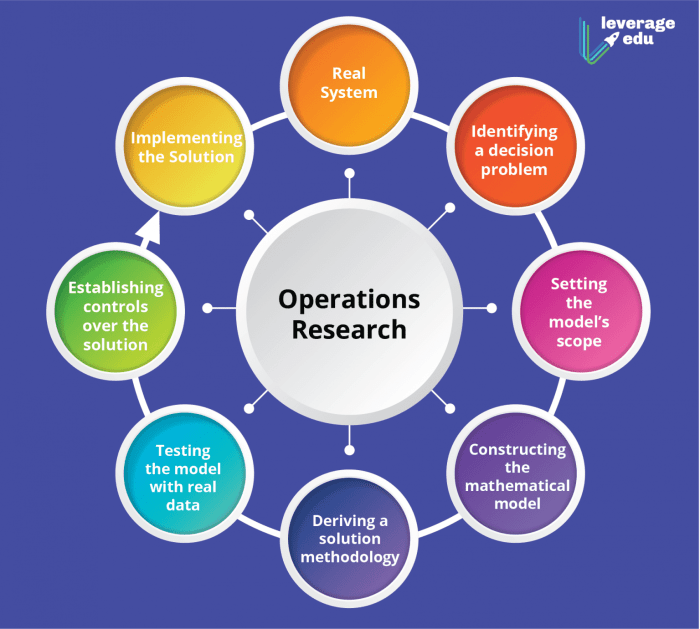
Riset operasi adalah pendekatan sistematis untuk memecahkan masalah kompleks dengan menggunakan model matematika dan teknik kuantitatif. Metode riset operasi membantu dalam pengambilan keputusan yang optimal, terutama dalam situasi yang melibatkan banyak variabel dan kendala.
Metode Riset Operasi yang Umum Digunakan
Metode riset operasi yang umum digunakan meliputi:
- Pemrograman Linear: Metode ini digunakan untuk memaksimalkan atau meminimalkan fungsi objektif dengan kendala linier. Contohnya, dalam perencanaan produksi, pemrograman linear dapat membantu menentukan jumlah produk yang harus diproduksi untuk memaksimalkan keuntungan dengan batasan sumber daya yang tersedia.
- Pemrograman Integer: Metode ini mirip dengan pemrograman linear, tetapi variabel keputusan dibatasi pada nilai integer. Contohnya, dalam penugasan karyawan, pemrograman integer dapat membantu menentukan jumlah karyawan yang harus ditugaskan ke setiap tugas dengan batasan jumlah karyawan yang tersedia.
- Pemrograman Dinamis: Metode ini memecahkan masalah kompleks dengan membaginya menjadi sub-masalah yang lebih kecil dan menyelesaikannya secara bertahap. Contohnya, dalam perencanaan investasi, pemrograman dinamis dapat membantu menentukan strategi investasi optimal dengan mempertimbangkan pengembalian investasi di masa depan.
- Teori Antrian: Metode ini digunakan untuk menganalisis dan mengoptimalkan sistem antrian, seperti di bank, supermarket, atau pusat panggilan. Contohnya, teori antrian dapat membantu menentukan jumlah kasir yang optimal untuk meminimalkan waktu tunggu pelanggan.
- Simulasi: Metode ini menggunakan model komputer untuk mensimulasikan sistem nyata dan menguji berbagai skenario. Contohnya, simulasi dapat digunakan untuk menguji efek perubahan desain pabrik terhadap efisiensi produksi.
Contoh Penerapan Metode Riset Operasi
Berikut adalah beberapa contoh penerapan metode riset operasi pada kasus-kasus nyata:
- Perencanaan Produksi: Pemrograman linear dapat digunakan untuk menentukan jumlah produk yang harus diproduksi untuk memaksimalkan keuntungan dengan batasan sumber daya yang tersedia. Contohnya, sebuah perusahaan manufaktur dapat menggunakan pemrograman linear untuk menentukan jumlah produk A, B, dan C yang harus diproduksi dengan batasan bahan baku, tenaga kerja, dan waktu produksi.
- Penugasan Karyawan: Pemrograman integer dapat digunakan untuk menentukan jumlah karyawan yang harus ditugaskan ke setiap tugas dengan batasan jumlah karyawan yang tersedia. Contohnya, sebuah perusahaan dapat menggunakan pemrograman integer untuk menentukan jumlah karyawan yang harus ditugaskan ke setiap shift dengan batasan jumlah karyawan yang tersedia di setiap shift.
- Perencanaan Investasi: Pemrograman dinamis dapat digunakan untuk menentukan strategi investasi optimal dengan mempertimbangkan pengembalian investasi di masa depan. Contohnya, seorang investor dapat menggunakan pemrograman dinamis untuk menentukan alokasi investasi optimal di berbagai aset, seperti saham, obligasi, dan properti.
- Manajemen Persediaan: Teori antrian dapat digunakan untuk menganalisis dan mengoptimalkan sistem antrian, seperti di bank, supermarket, atau pusat panggilan. Contohnya, sebuah bank dapat menggunakan teori antrian untuk menentukan jumlah kasir yang optimal untuk meminimalkan waktu tunggu pelanggan.
- Pengambilan Keputusan Logistik: Simulasi dapat digunakan untuk menguji efek perubahan desain pabrik terhadap efisiensi produksi. Contohnya, sebuah perusahaan manufaktur dapat menggunakan simulasi untuk menguji efek perubahan tata letak pabrik terhadap waktu produksi dan biaya operasional.
Kelebihan dan Kekurangan Metode Riset Operasi
Berikut adalah tabel yang menunjukkan kelebihan dan kekurangan masing-masing metode riset operasi:
| Metode | Kelebihan | Kekurangan |
|---|---|---|
| Pemrograman Linear | – Mudah dipahami dan diterapkan. – Dapat menangani masalah dengan banyak variabel dan kendala. – Memberikan solusi optimal. |
– Asumsi linieritas mungkin tidak selalu berlaku dalam dunia nyata. – Tidak dapat menangani masalah dengan variabel integer. |
| Pemrograman Integer | – Dapat menangani masalah dengan variabel integer. – Memberikan solusi optimal. |
– Lebih kompleks daripada pemrograman linear. – Membutuhkan waktu komputasi yang lebih lama. |
| Pemrograman Dinamis | – Dapat memecahkan masalah kompleks dengan membaginya menjadi sub-masalah yang lebih kecil. – Memberikan solusi optimal. |
– Membutuhkan pemahaman yang mendalam tentang masalah. – Tidak semua masalah dapat dipecahkan dengan pemrograman dinamis. |
| Teori Antrian | – Dapat menganalisis dan mengoptimalkan sistem antrian. – Memberikan solusi optimal untuk meminimalkan waktu tunggu pelanggan. |
– Asumsi model antrian mungkin tidak selalu berlaku dalam dunia nyata. – Membutuhkan data yang akurat tentang sistem antrian. |
| Simulasi | – Dapat mensimulasikan sistem nyata dan menguji berbagai skenario. – Tidak membutuhkan asumsi linieritas. |
– Membutuhkan waktu komputasi yang lama. – Tidak selalu memberikan solusi optimal. |
Model Riset Operasi
Riset operasi adalah disiplin ilmu yang menggunakan metode ilmiah untuk memecahkan masalah kompleks yang dihadapi oleh organisasi. Salah satu aspek penting dalam riset operasi adalah penggunaan model, yang merupakan representasi matematis dari sistem nyata yang ingin dikaji. Model riset operasi dapat membantu kita memahami sistem, memprediksi perilaku, dan menemukan solusi optimal untuk masalah yang dihadapi.
Perbedaan Model Deterministik dan Stokastik
Model riset operasi dapat dikategorikan menjadi dua jenis utama: deterministik dan stokastik. Perbedaan mendasar terletak pada bagaimana kedua model ini memperlakukan ketidakpastian.
- Model Deterministik: Model ini mengasumsikan bahwa semua parameter dan input diketahui dengan pasti. Artinya, tidak ada unsur ketidakpastian dalam model. Contohnya adalah model perencanaan produksi yang mengasumsikan bahwa permintaan produk diketahui dengan pasti.
- Model Stokastik: Model ini mempertimbangkan ketidakpastian dalam parameter dan input. Ketidakpastian ini direpresentasikan dengan menggunakan variabel acak. Contohnya adalah model manajemen inventaris yang mempertimbangkan variasi permintaan yang tidak pasti.
Contoh Model Riset Operasi
Model riset operasi memiliki aplikasi yang luas di berbagai bidang. Berikut adalah beberapa contoh umum:
- Transportasi: Model riset operasi dapat digunakan untuk mengoptimalkan rute pengiriman, mengatur jadwal transportasi, dan menentukan kapasitas kendaraan yang optimal. Misalnya, model transportasi dapat digunakan untuk menemukan rute terpendek untuk pengiriman barang dari gudang ke toko-toko.
- Produksi: Model riset operasi dapat membantu dalam perencanaan produksi, penjadwalan, dan pengendalian inventaris. Misalnya, model perencanaan produksi dapat digunakan untuk menentukan jumlah produk yang harus diproduksi untuk memenuhi permintaan yang diprediksi.
- Keuangan: Model riset operasi dapat digunakan untuk mengelola portofolio investasi, menentukan strategi pembiayaan, dan meminimalkan risiko keuangan. Misalnya, model portofolio investasi dapat digunakan untuk menentukan proporsi aset yang harus diinvestasikan di berbagai kelas aset untuk mencapai tingkat pengembalian yang diinginkan dengan risiko minimum.
Langkah-langkah Membangun Model Riset Operasi
Membangun model riset operasi melibatkan beberapa langkah yang sistematis. Berikut adalah langkah-langkah umum yang terlibat:
- Identifikasi Masalah: Langkah pertama adalah mengidentifikasi masalah yang ingin dipecahkan. Penting untuk mendefinisikan dengan jelas tujuan yang ingin dicapai dengan model.
- Pengumpulan Data: Setelah masalah teridentifikasi, langkah selanjutnya adalah mengumpulkan data yang relevan. Data ini akan digunakan untuk membangun model dan memvalidasi hasilnya.
- Formulasi Model: Langkah ini melibatkan pembentukan model matematis yang merepresentasikan sistem nyata. Model ini biasanya terdiri dari persamaan dan variabel yang mewakili hubungan antara berbagai elemen dalam sistem.
- Solusi Model: Setelah model diformulasikan, langkah selanjutnya adalah mencari solusi optimal. Solusi ini dapat berupa nilai optimal untuk variabel-variabel dalam model yang memaksimalkan atau meminimalkan tujuan yang ingin dicapai.
- Validasi Model: Setelah solusi diperoleh, langkah selanjutnya adalah memvalidasi model. Validasi melibatkan membandingkan hasil model dengan data nyata untuk memastikan bahwa model akurat dan dapat diandalkan.
- Implementasi dan Interpretasi Hasil: Langkah terakhir adalah mengimplementasikan solusi yang diperoleh dari model dan menginterpretasikan hasilnya. Implementasi melibatkan penerapan solusi dalam sistem nyata, sementara interpretasi melibatkan analisis dan pemahaman tentang hasil model.
Soal Riset Operasi
Riset operasi adalah disiplin ilmu yang menggunakan metode kuantitatif untuk membantu pengambilan keputusan yang optimal. Salah satu penerapan riset operasi yang umum adalah dalam masalah transportasi, di mana tujuannya adalah untuk meminimalkan biaya pengiriman barang dari beberapa sumber ke beberapa tujuan. Dalam contoh soal ini, kita akan membahas masalah transportasi dengan skenario pengiriman barang dari beberapa gudang ke beberapa toko.
Contoh Soal Riset Operasi: Masalah Transportasi
Sebuah perusahaan memiliki tiga gudang (A, B, dan C) yang menyimpan produk yang sama. Perusahaan ini harus mengirimkan produk tersebut ke empat toko (D, E, F, dan G). Tabel berikut menunjukkan kapasitas setiap gudang, permintaan setiap toko, dan biaya pengiriman per unit produk dari setiap gudang ke setiap toko.
| D | E | F | G | Kapasitas | |
|---|---|---|---|---|---|
| A | $5 | $7 | $4 | $6 | 100 |
| B | $6 | $4 | $5 | $8 | 150 |
| C | $8 | $6 | $7 | $5 | 200 |
| Permintaan | 80 | 120 | 100 | 150 |
Tentukan berapa banyak unit produk yang harus dikirim dari setiap gudang ke setiap toko untuk meminimalkan biaya total pengiriman.
Penyelesaian Soal
Untuk menyelesaikan masalah transportasi ini, kita dapat menggunakan metode simplex. Langkah-langkah penyelesaiannya adalah sebagai berikut:
1. Definisikan Variabel
- Xij: Jumlah unit produk yang dikirim dari gudang i ke toko j.
2. Fungsi Objektif
Fungsi objektif adalah fungsi yang ingin kita minimalkan. Dalam kasus ini, fungsi objektif adalah biaya total pengiriman, yang dapat dirumuskan sebagai berikut:
Minimize Z = 5XAD + 7XAE + 4XAF + 6XAG + 6XBD + 4XBE + 5XBF + 8XBG + 8XCD + 6XCE + 7XCF + 5XCG
3. Kendala
Kendala adalah batasan yang harus dipenuhi dalam masalah ini. Kendala yang ada meliputi:
- Kendala kapasitas gudang:
- XAD + XAE + XAF + XAG ≤ 100 (Gudang A)
- XBD + XBE + XBF + XBG ≤ 150 (Gudang B)
- XCD + XCE + XCF + XCG ≤ 200 (Gudang C)
- Kendala permintaan toko:
- XAD + XBD + XCD = 80 (Toko D)
- XAE + XBE + XCE = 120 (Toko E)
- XAF + XBF + XCF = 100 (Toko F)
- XAG + XBG + XCG = 150 (Toko G)
- Kendala non-negatif:
- Xij ≥ 0 (untuk semua i dan j)
4. Solusi Optimal
Untuk menemukan solusi optimal, kita dapat menggunakan metode simplex. Metode simplex adalah algoritma iteratif yang bertujuan untuk menemukan solusi optimal dengan secara bertahap meningkatkan nilai fungsi objektif sambil memenuhi semua kendala.
Dengan menggunakan metode simplex, kita dapat memperoleh solusi optimal untuk masalah transportasi ini, yang menunjukkan berapa banyak unit produk yang harus dikirim dari setiap gudang ke setiap toko untuk meminimalkan biaya total pengiriman.
Soal Riset Operasi: Masalah Penugasan
Masalah penugasan merupakan salah satu contoh klasik dalam riset operasi yang melibatkan penugasan sumber daya terbatas (misalnya pekerja) ke berbagai tugas dengan tujuan memaksimalkan efisiensi atau meminimalkan biaya. Model ini memiliki aplikasi luas dalam berbagai bidang, seperti manajemen produksi, penjadwalan proyek, dan alokasi sumber daya.
Contoh Soal Penugasan
Berikut contoh soal riset operasi tentang masalah penugasan:
Sebuah perusahaan memiliki empat pekerja (A, B, C, dan D) yang harus ditugaskan ke empat tugas (1, 2, 3, dan 4). Setiap pekerja memiliki kemampuan yang berbeda-beda dalam menyelesaikan setiap tugas, yang diukur dalam waktu yang dibutuhkan (dalam jam) seperti pada tabel berikut:
| Tugas | A | B | C | D |
|---|---|---|---|---|
| 1 | 10 | 8 | 9 | 12 |
| 2 | 12 | 10 | 11 | 14 |
| 3 | 8 | 9 | 10 | 11 |
| 4 | 9 | 11 | 12 | 13 |
Bagaimana cara menugaskan pekerja ke tugas agar total waktu yang dibutuhkan untuk menyelesaikan semua tugas diminimalkan?
Contoh soal riset operasi biasanya membahas tentang optimasi, seperti mencari cara terbaik untuk mengalokasikan sumber daya. Misalnya, bagaimana menentukan jumlah produk yang harus diproduksi untuk memaksimalkan keuntungan. Nah, kalau kamu tertarik untuk mempelajari contoh soal yang berkaitan dengan perubahan suatu zat seiring waktu, kamu bisa cek contoh soal laju reaksi ini.
Konsep laju reaksi ini juga bisa diterapkan dalam riset operasi, misalnya untuk memodelkan proses produksi atau pergerakan material.
Merumuskan Masalah Penugasan sebagai Model Riset Operasi
Untuk merumuskan masalah penugasan sebagai model riset operasi, kita perlu mendefinisikan:
- Variabel keputusan: Variabel keputusan dalam masalah penugasan adalah penugasan pekerja ke tugas. Kita dapat menggunakan variabel biner xij untuk merepresentasikan penugasan, di mana:
- xij = 1 jika pekerja i ditugaskan ke tugas j
- xij = 0 jika pekerja i tidak ditugaskan ke tugas j
- Fungsi tujuan: Fungsi tujuan dalam masalah penugasan adalah meminimalkan total waktu yang dibutuhkan untuk menyelesaikan semua tugas. Kita dapat menyatakan fungsi tujuan sebagai:
- Kendala: Kendala dalam masalah penugasan memastikan bahwa setiap pekerja ditugaskan ke tepat satu tugas, dan setiap tugas hanya dikerjakan oleh satu pekerja. Kendala ini dapat ditulis sebagai:
- ∑j=1n xij = 1 untuk setiap pekerja i (setiap pekerja ditugaskan ke satu tugas)
- ∑i=1n xij = 1 untuk setiap tugas j (setiap tugas dikerjakan oleh satu pekerja)
Minimize ∑i=1n ∑j=1n cij xij
di mana cij adalah waktu yang dibutuhkan oleh pekerja i untuk menyelesaikan tugas j.
Langkah-langkah Penyelesaian Soal Menggunakan Metode Hungarian
Metode Hungarian adalah algoritma yang efisien untuk menyelesaikan masalah penugasan. Berikut adalah langkah-langkahnya:
- Buat matriks biaya: Matriks biaya berisi waktu yang dibutuhkan oleh setiap pekerja untuk menyelesaikan setiap tugas.
- Kurangi setiap baris dengan nilai minimum di baris tersebut: Langkah ini bertujuan untuk membuat setidaknya satu nol di setiap baris.
- Kurangi setiap kolom dengan nilai minimum di kolom tersebut: Langkah ini bertujuan untuk membuat setidaknya satu nol di setiap kolom.
- Tarik garis horizontal dan vertikal minimal untuk menutup semua nol: Garis harus ditarik sedemikian rupa sehingga jumlah garis minimal.
- Jika jumlah garis sama dengan jumlah pekerja atau tugas, maka solusi optimal telah ditemukan: Solusi optimal ditunjukkan oleh nol yang tidak tertutup oleh garis.
- Jika jumlah garis kurang dari jumlah pekerja atau tugas, maka lanjutkan ke langkah 7:
- Temukan nilai minimum dari semua angka yang tidak tertutup garis: Kurangi semua angka yang tidak tertutup garis dengan nilai minimum tersebut, dan tambahkan nilai minimum tersebut ke angka-angka yang terletak pada perpotongan garis.
- Ulangi langkah 4-7 hingga solusi optimal ditemukan:
Soal Riset Operasi: Masalah Antrian
Masalah antrian merupakan salah satu topik penting dalam riset operasi. Model antrian membantu kita memahami dan menganalisis perilaku sistem pelayanan yang melibatkan antrian, seperti bank, restoran, atau pusat panggilan. Dengan memahami model antrian, kita dapat mengoptimalkan kinerja sistem pelayanan dan meningkatkan kepuasan pelanggan.
Contoh Soal Masalah Antrian, Contoh soal riset operasi
Berikut ini adalah contoh soal riset operasi yang membahas masalah antrian:
Sebuah bank memiliki satu teller yang melayani pelanggan. Pelanggan datang ke bank dengan rata-rata 5 orang per jam, dan teller dapat melayani 8 orang per jam. Asumsikan bahwa kedatangan dan pelayanan pelanggan mengikuti distribusi Poisson.
Parameter dalam Model Antrian
Dalam model antrian, beberapa parameter penting yang perlu diperhatikan, antara lain:
- Tingkat kedatangan (λ): Jumlah rata-rata pelanggan yang datang ke sistem per unit waktu. Dalam contoh soal di atas, tingkat kedatangan adalah 5 orang per jam.
- Tingkat pelayanan (μ): Jumlah rata-rata pelanggan yang dapat dilayani per unit waktu. Dalam contoh soal di atas, tingkat pelayanan adalah 8 orang per jam.
- Jumlah server (s): Jumlah teller atau petugas yang melayani pelanggan. Dalam contoh soal di atas, jumlah server adalah 1.
- Kapasitas sistem (N): Jumlah maksimum pelanggan yang dapat berada dalam sistem (termasuk yang sedang dilayani dan yang sedang menunggu). Dalam contoh soal di atas, kapasitas sistem tidak disebutkan, sehingga dapat diasumsikan tidak terbatas.
Analisis Kinerja Sistem Antrian
Setelah menentukan parameter model antrian, kita dapat menganalisis kinerja sistem antrian. Beberapa metrik penting yang digunakan untuk mengukur kinerja sistem antrian, antara lain:
- Waktu tunggu rata-rata (Wq): Waktu rata-rata yang dibutuhkan pelanggan untuk menunggu di antrian sebelum dilayani.
- Waktu dalam sistem rata-rata (Ws): Waktu rata-rata yang dibutuhkan pelanggan dalam sistem, termasuk waktu menunggu dan waktu pelayanan.
- Jumlah pelanggan dalam sistem rata-rata (L): Jumlah rata-rata pelanggan yang berada dalam sistem, termasuk yang sedang dilayani dan yang sedang menunggu.
- Probabilitas antrian (Pw): Probabilitas bahwa pelanggan harus menunggu di antrian sebelum dilayani.
Contoh Soal Analisis Kinerja Sistem Antrian
Berangkat dari contoh soal sebelumnya, kita dapat menghitung metrik kinerja sistem antrian menggunakan rumus-rumus yang telah tersedia. Misalnya, waktu tunggu rata-rata (Wq) dapat dihitung menggunakan rumus:
Wq = λ / (μ(μ-λ))
Dengan memasukkan nilai λ = 5 dan μ = 8, maka waktu tunggu rata-rata adalah:
Wq = 5 / (8(8-5)) = 0,56 jam
Artinya, pelanggan rata-rata harus menunggu selama 0,56 jam (sekitar 34 menit) sebelum dilayani.
Soal Riset Operasi: Masalah Inventaris: Contoh Soal Riset Operasi
Riset operasi sering digunakan untuk memecahkan masalah inventaris dalam bisnis. Salah satu contohnya adalah menentukan jumlah persediaan optimal yang harus dipesan untuk meminimalkan biaya total yang terkait dengan inventaris.
Contoh Soal Riset Operasi Masalah Inventaris
Perusahaan ABC adalah perusahaan yang memproduksi dan menjual produk elektronik. Perusahaan ini ingin menentukan jumlah persediaan optimal untuk komponen utama produknya, yaitu baterai. Berikut adalah informasi yang tersedia:
- Permintaan tahunan untuk baterai: 10.000 unit
- Biaya pemesanan per pesanan: Rp 50.000
- Biaya penyimpanan per unit per tahun: Rp 10.000
Berapakah jumlah persediaan optimal yang harus dipesan oleh perusahaan ABC setiap kali?
Biaya yang Terkait dengan Inventaris
Ada beberapa biaya yang terkait dengan inventaris, yaitu:
- Biaya pemesanan: Biaya yang dikeluarkan untuk setiap pesanan, termasuk biaya administrasi, biaya pengiriman, dan biaya penanganan.
- Biaya penyimpanan: Biaya yang dikeluarkan untuk menyimpan inventaris, termasuk biaya sewa gudang, biaya asuransi, dan biaya kerusakan.
- Biaya kekurangan: Biaya yang dikeluarkan karena kehabisan inventaris, termasuk biaya kehilangan penjualan, biaya produksi terhenti, dan biaya pengiriman ekspres.
Model EOQ (Economic Order Quantity)
Model EOQ adalah model yang digunakan untuk menentukan jumlah persediaan optimal yang harus dipesan setiap kali. Model ini bertujuan untuk meminimalkan biaya total yang terkait dengan inventaris, yaitu biaya pemesanan dan biaya penyimpanan.
Rumus EOQ adalah:
EOQ = √(2DS/H)
Dimana:
- D = Permintaan tahunan
- S = Biaya pemesanan per pesanan
- H = Biaya penyimpanan per unit per tahun
Langkah-langkah Penyelesaian Soal
Berikut adalah langkah-langkah penyelesaian soal riset operasi masalah inventaris menggunakan model EOQ:
- Tentukan permintaan tahunan (D), biaya pemesanan per pesanan (S), dan biaya penyimpanan per unit per tahun (H).
- Substitusikan nilai-nilai tersebut ke dalam rumus EOQ.
- Hitung jumlah persediaan optimal (EOQ).
Dalam contoh soal sebelumnya, perusahaan ABC memiliki permintaan tahunan (D) sebesar 10.000 unit, biaya pemesanan per pesanan (S) sebesar Rp 50.000, dan biaya penyimpanan per unit per tahun (H) sebesar Rp 10.000.
Maka, jumlah persediaan optimal (EOQ) yang harus dipesan oleh perusahaan ABC setiap kali adalah:
EOQ = √(2 * 10.000 * 50.000 / 10.000) = 100 unit
Jadi, perusahaan ABC harus memesan 100 unit baterai setiap kali untuk meminimalkan biaya total yang terkait dengan inventaris.
Soal Riset Operasi: Masalah Pengambilan Keputusan
Pengambilan keputusan merupakan hal yang krusial dalam dunia bisnis. Riset operasi menyediakan berbagai metode dan alat untuk membantu perusahaan dalam memilih strategi terbaik yang menguntungkan dan efisien. Salah satu contohnya adalah masalah pengambilan keputusan, yang seringkali melibatkan berbagai faktor dan ketidakpastian.
Contoh Soal Masalah Pengambilan Keputusan
Bayangkan sebuah perusahaan manufaktur yang ingin meluncurkan produk baru. Mereka memiliki dua pilihan strategi pemasaran:
- Strategi A: Meluncurkan produk dengan kampanye iklan masif di televisi dan media sosial.
- Strategi B: Meluncurkan produk dengan fokus pada pemasaran digital dan influencer marketing.
Setiap strategi memiliki keuntungan dan kerugiannya masing-masing. Perusahaan perlu mempertimbangkan berbagai faktor, seperti biaya, potensi pasar, dan risiko, untuk menentukan strategi terbaik.
Metode Pengambilan Keputusan
Beberapa metode pengambilan keputusan yang dapat digunakan dalam kasus ini adalah:
- Analisis Sensitivitas: Metode ini membantu perusahaan untuk memahami bagaimana perubahan dalam asumsi atau variabel kunci akan mempengaruhi hasil akhir. Misalnya, perusahaan dapat menganalisis bagaimana perubahan biaya produksi akan mempengaruhi keuntungan dari masing-masing strategi pemasaran.
- Analisis Risiko: Metode ini membantu perusahaan untuk mengidentifikasi dan menilai risiko yang terkait dengan setiap strategi. Misalnya, perusahaan dapat menganalisis risiko kegagalan kampanye iklan atau risiko kehilangan pasar akibat persaingan.
- Analisis Pohon Keputusan: Metode ini membantu perusahaan untuk memvisualisasikan berbagai kemungkinan hasil dari setiap strategi. Pohon keputusan terdiri dari serangkaian node yang mewakili keputusan atau kejadian, dan cabang yang mewakili kemungkinan hasil dari setiap keputusan atau kejadian.
Penerapan Analisis Pohon Keputusan
Contoh soal penerapan analisis pohon keputusan dalam pengambilan keputusan:
Sebuah perusahaan ingin meluncurkan produk baru dengan dua pilihan strategi pemasaran: strategi A dan strategi B. Setiap strategi memiliki kemungkinan berhasil dan gagal, dengan hasil keuntungan dan kerugian yang berbeda.
Berikut adalah contoh pohon keputusan yang dapat digunakan untuk menganalisis situasi ini:
| Keputusan | Hasil | Probabilitas | Keuntungan/Kerugian |
|---|---|---|---|
| Strategi A | Sukses | 0.6 | Rp 100.000.000 |
| Gagal | 0.4 | -Rp 50.000.000 | |
| Strategi B | Sukses | 0.5 | Rp 75.000.000 |
| Gagal | 0.5 | -Rp 25.000.000 |
Dengan menggunakan analisis pohon keputusan, perusahaan dapat menghitung nilai harapan (expected value) dari setiap strategi dan memilih strategi dengan nilai harapan tertinggi.
Kesimpulan
Riset operasi, dengan metode dan modelnya yang beragam, menawarkan alat yang ampuh untuk menyelesaikan masalah kompleks. Dengan memahami dasar-dasar riset operasi dan mampu menerapkannya, Anda akan mampu membuat keputusan yang lebih cerdas dan efisien dalam berbagai situasi. Mulai dari meningkatkan efisiensi operasional hingga menemukan solusi optimal untuk masalah bisnis, riset operasi membuka jalan menuju hasil yang lebih baik.