Contoh soal simpangan baku data tunggal – Pernahkah kamu bertanya-tanya bagaimana mengukur sebaran data? Misalnya, jika kamu ingin mengetahui variasi tinggi badan siswa dalam kelas, simpangan baku bisa menjadi alat yang tepat. Simpangan baku data tunggal adalah ukuran statistik yang menunjukkan seberapa jauh data menyebar dari nilai rata-ratanya. Semakin besar nilai simpangan baku, semakin besar penyebaran datanya.
Dalam artikel ini, kita akan membahas contoh soal simpangan baku data tunggal dan bagaimana cara menghitungnya. Kita akan mempelajari rumus, langkah-langkah, dan penerapannya dalam kehidupan sehari-hari. Yuk, kita telusuri lebih dalam tentang simpangan baku data tunggal!
Pengertian Simpangan Baku Data Tunggal
Simpangan baku adalah ukuran seberapa tersebar data dari nilai rata-ratanya. Semakin besar simpangan baku, semakin tersebar data, dan sebaliknya. Dalam data tunggal, kita hanya memiliki satu nilai, sehingga kita tidak dapat menghitung simpangan baku secara langsung. Namun, kita dapat menghitung simpangan baku dari data tunggal dengan mengasumsikan bahwa data tersebut merupakan sampel dari populasi yang lebih besar.
Nah, kalau lagi belajar tentang simpangan baku data tunggal, kamu bisa coba kerjakan contoh soal yang menghitung seberapa jauh nilai data dari rata-ratanya. Ingat, simpangan baku ini penting untuk melihat sebaran data, lho! Nah, kalau kamu lagi belajar tentang genetika, kamu bisa cek contoh soal persilangan monohibrid kelas 9 di link ini.
Soal-soal ini akan membantumu memahami konsep persilangan antara dua individu dengan satu sifat beda. Nah, kembali ke simpangan baku, kamu bisa belajar menghitungnya dengan menggunakan rumus yang sudah kamu pelajari. Pastikan kamu paham rumusnya dan bisa menerapkannya dalam contoh soal, ya!
Cara Menghitung Simpangan Baku Data Tunggal
Untuk menghitung simpangan baku data tunggal, kita perlu mengetahui rata-rata dan jumlah data dari populasi yang lebih besar. Kemudian, kita dapat menggunakan rumus berikut:
σ = √(∑(x – μ)² / N)
Dimana:
- σ adalah simpangan baku
- x adalah nilai data tunggal
- μ adalah rata-rata populasi
- N adalah jumlah data populasi
Contohnya, jika kita memiliki data tunggal 10 dan kita tahu bahwa rata-rata populasi adalah 8 dan jumlah data populasi adalah 100, maka simpangan baku data tunggal adalah:
σ = √((10 – 8)² / 100) = √(4 / 100) = 0.2
Perbedaan Simpangan Baku, Rata-rata, dan Jangkauan
Simpangan baku, rata-rata, dan jangkauan adalah ukuran statistik yang berbeda yang memberikan informasi yang berbeda tentang data. Rata-rata adalah nilai tengah dari data, sedangkan jangkauan adalah selisih antara nilai terbesar dan terkecil dari data. Simpangan baku adalah ukuran seberapa tersebar data dari nilai rata-ratanya.
Perbedaan utama antara simpangan baku dan rata-rata adalah bahwa rata-rata menunjukkan nilai tengah data, sedangkan simpangan baku menunjukkan seberapa tersebar data dari nilai tengah tersebut. Jangkauan, di sisi lain, menunjukkan rentang nilai data.
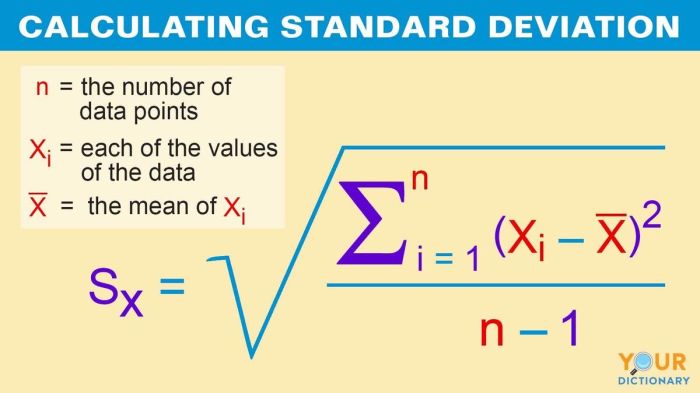
Rumus Simpangan Baku Data Tunggal
Simpangan baku merupakan ukuran sebaran data yang menunjukkan seberapa jauh nilai data menyebar dari nilai rata-ratanya. Semakin besar nilai simpangan baku, semakin besar sebaran data.
Rumus Menghitung Simpangan Baku Data Tunggal
Rumus menghitung simpangan baku data tunggal adalah sebagai berikut:
$$s = \sqrt\frac\sum_i=1^n(x_i – \barx)^2n-1$$
Keterangan:
- s adalah simpangan baku
- xi adalah nilai data ke-i
- x̄ adalah rata-rata data
- n adalah jumlah data
Contoh Soal Menghitung Simpangan Baku Data Tunggal
Misalkan terdapat data tinggi badan 5 siswa sebagai berikut: 160 cm, 165 cm, 170 cm, 175 cm, dan 180 cm. Hitunglah simpangan baku data tersebut!
Langkah-langkah penyelesaian:
1. Hitung rata-rata data.
$$\barx = \frac160 + 165 + 170 + 175 + 1805 = 170$$
2. Hitung selisih setiap nilai data dengan rata-rata, kemudian kuadratkan.
| xi | xi – x̄ | (xi – x̄)2 |
|---|---|---|
| 160 | -10 | 100 |
| 165 | -5 | 25 |
| 170 | 0 | 0 |
| 175 | 5 | 25 |
| 180 | 10 | 100 |
3. Jumlahkan semua nilai (xi – x̄)2.
$$\sum_i=1^n(x_i – \barx)^2 = 100 + 25 + 0 + 25 + 100 = 250$$
4. Hitung simpangan baku dengan rumus:
$$s = \sqrt\frac\sum_i=1^n(x_i – \barx)^2n-1 = \sqrt\frac2505-1 = \sqrt62.5 \approx 7.91$$
Jadi, simpangan baku data tinggi badan 5 siswa tersebut adalah 7.91 cm.
Cara Menghitung Simpangan Baku Data Tunggal
Simpangan baku merupakan ukuran sebaran data yang menunjukkan sejauh mana data menyebar dari rata-rata. Dalam data tunggal, simpangan baku dapat dihitung dengan langkah-langkah yang mudah dipahami. Mari kita bahas langkah-langkahnya dan contohnya!
Langkah-langkah Menghitung Simpangan Baku Data Tunggal, Contoh soal simpangan baku data tunggal
Berikut adalah langkah-langkah menghitung simpangan baku data tunggal:
- Hitung rata-rata data tunggal. Rata-rata diperoleh dengan menjumlahkan semua data kemudian dibagi dengan jumlah data.
- Hitung selisih setiap data dengan rata-rata. Ini berarti mengurangi rata-rata dari setiap data.
- Kuadratkan setiap selisih yang diperoleh pada langkah sebelumnya.
- Hitung jumlah kuadrat selisih.
- Bagi jumlah kuadrat selisih dengan jumlah data dikurangi satu.
- Akar kuadratkan hasil pada langkah sebelumnya. Hasil ini adalah simpangan baku data tunggal.
Contoh Menghitung Simpangan Baku Data Tunggal
Misalkan kita memiliki data tunggal sebagai berikut: 2, 4, 6, 8, 10. Mari kita hitung simpangan bakunya dengan mengikuti langkah-langkah di atas.
- Rata-rata data: (2 + 4 + 6 + 8 + 10) / 5 = 6
- Selisih setiap data dengan rata-rata:
- 2 – 6 = -4
- 4 – 6 = -2
- 6 – 6 = 0
- 8 – 6 = 2
- 10 – 6 = 4
- Kuadratkan setiap selisih:
- (-4)^2 = 16
- (-2)^2 = 4
- (0)^2 = 0
- (2)^2 = 4
- (4)^2 = 16
- Jumlah kuadrat selisih: 16 + 4 + 0 + 4 + 16 = 40
- Bagi jumlah kuadrat selisih dengan jumlah data dikurangi satu: 40 / (5 – 1) = 10
- Akar kuadratkan hasil pada langkah sebelumnya: √10 ≈ 3.16
Jadi, simpangan baku data tunggal 2, 4, 6, 8, 10 adalah sekitar 3.16.
Menghitung Simpangan Baku dengan Kalkulator atau Software Statistik
Menghitung simpangan baku dengan kalkulator atau software statistik dapat mempermudah prosesnya. Kebanyakan kalkulator ilmiah dan software statistik memiliki fungsi khusus untuk menghitung simpangan baku. Berikut adalah langkah-langkah umum:
- Masukkan data tunggal ke dalam kalkulator atau software statistik.
- Pilih fungsi “simpangan baku” atau “standar deviasi”.
- Tekan tombol “enter” atau “hitung” untuk mendapatkan hasil simpangan baku.
Perhatikan bahwa beberapa kalkulator dan software statistik mungkin menggunakan rumus yang sedikit berbeda untuk menghitung simpangan baku. Pastikan Anda memahami cara kerja kalkulator atau software statistik yang Anda gunakan.
Soal Latihan Simpangan Baku Data Tunggal
Simpangan baku merupakan ukuran sebaran data yang menunjukkan seberapa jauh nilai data menyimpang dari rata-rata. Semakin besar nilai simpangan baku, semakin besar sebaran datanya. Dalam data tunggal, kita bisa menghitung simpangan baku dengan rumus yang mudah. Berikut ini beberapa soal latihan yang bisa kamu kerjakan untuk mengasah pemahamanmu tentang simpangan baku data tunggal.
Soal Latihan
Berikut ini 5 soal latihan tentang menghitung simpangan baku data tunggal dengan tingkat kesulitan yang berbeda.
- Hitunglah simpangan baku dari data tunggal berikut: 5, 7, 8, 9, 10.
- Nilai ulangan matematika dari 5 siswa adalah 7, 8, 9, 10, dan 6. Hitunglah simpangan baku nilai ulangan matematika tersebut.
- Tinggi badan 4 orang siswa adalah 160 cm, 165 cm, 170 cm, dan 175 cm. Tentukan simpangan baku tinggi badan keempat siswa tersebut.
- Data tunggal berikut menunjukkan nilai ujian Bahasa Indonesia dari 6 siswa: 70, 80, 90, 85, 75, dan 85. Hitunglah simpangan baku data tersebut.
- Suhu udara di suatu kota selama 5 hari berturut-turut adalah 25°C, 28°C, 30°C, 27°C, dan 26°C. Tentukan simpangan baku suhu udara di kota tersebut.
Kunci Jawaban
Berikut ini kunci jawaban dari soal latihan di atas.
- Rata-rata data = (5 + 7 + 8 + 9 + 10) / 5 = 7.8
Simpangan baku = √[( (5-7.8)² + (7-7.8)² + (8-7.8)² + (9-7.8)² + (10-7.8)² ) / 5] = √(11.2) = 3.35 - Rata-rata data = (7 + 8 + 9 + 10 + 6) / 5 = 8
Simpangan baku = √[( (7-8)² + (8-8)² + (9-8)² + (10-8)² + (6-8)² ) / 5] = √(4) = 2 - Rata-rata data = (160 + 165 + 170 + 175) / 4 = 167.5
Simpangan baku = √[( (160-167.5)² + (165-167.5)² + (170-167.5)² + (175-167.5)² ) / 4] = √(56.25) = 7.5 - Rata-rata data = (70 + 80 + 90 + 85 + 75 + 85) / 6 = 80.83
Simpangan baku = √[( (70-80.83)² + (80-80.83)² + (90-80.83)² + (85-80.83)² + (75-80.83)² + (85-80.83)² ) / 6] = √(54.17) = 7.36 - Rata-rata data = (25 + 28 + 30 + 27 + 26) / 5 = 27.2
Simpangan baku = √[( (25-27.2)² + (28-27.2)² + (30-27.2)² + (27-27.2)² + (26-27.2)² ) / 5] = √(3.36) = 1.83
Tabel Rumus dan Langkah
Berikut ini tabel yang berisi rangkuman rumus dan langkah-langkah menghitung simpangan baku data tunggal.
| Rumus | Langkah-langkah |
|---|---|
|
|
Ilustrasi Konsep Simpangan Baku Data Tunggal
Simpangan baku adalah ukuran seberapa tersebar data dari nilai rata-ratanya. Dalam konteks data tunggal, simpangan baku memberikan gambaran tentang seberapa jauh nilai tunggal tersebut dari nilai tengah. Semakin besar simpangan baku, semakin tersebar data, dan sebaliknya.
Hubungan Simpangan Baku dengan Penyebaran Data
Diagram berikut menggambarkan hubungan antara simpangan baku dengan penyebaran data tunggal:
Bayangkan sebuah garis lurus yang mewakili nilai rata-rata data. Titik pada garis mewakili nilai data tunggal. Semakin jauh titik dari garis, semakin besar simpangan bakunya.
Misalnya, jika kita memiliki dua data tunggal dengan nilai 5 dan 10, dan nilai rata-ratanya adalah 7,5, maka simpangan baku dari data 5 adalah 2,5 dan simpangan baku dari data 10 adalah 2,5. Hal ini menunjukkan bahwa kedua data tersebut sama-sama jauh dari nilai rata-rata, sehingga simpangan bakunya sama.
Nilai Simpangan Baku Mengindikasikan Tingkat Variasi Data
Nilai simpangan baku dapat mengindikasikan tingkat variasi data tunggal. Semakin tinggi nilai simpangan baku, semakin besar variasi data, dan sebaliknya.
Misalnya, jika kita memiliki dua data tunggal dengan nilai 5 dan 10, dan nilai rata-ratanya adalah 7,5, maka simpangan baku dari kedua data tersebut adalah 2,5. Hal ini menunjukkan bahwa kedua data tersebut memiliki tingkat variasi yang sama, yaitu 2,5 dari nilai rata-rata.
Perbedaan Data Tunggal dengan Simpangan Baku Tinggi dan Rendah
Berikut adalah contoh ilustrasi yang menunjukkan perbedaan antara data tunggal dengan simpangan baku yang tinggi dan rendah:
- Data tunggal dengan simpangan baku yang tinggi menunjukkan bahwa data tersebut sangat bervariasi dari nilai rata-ratanya. Misalnya, jika kita memiliki data tunggal dengan nilai 10 dan nilai rata-ratanya adalah 5, maka simpangan bakunya adalah 5. Hal ini menunjukkan bahwa data tersebut sangat bervariasi dari nilai rata-rata.
- Data tunggal dengan simpangan baku yang rendah menunjukkan bahwa data tersebut tidak terlalu bervariasi dari nilai rata-ratanya. Misalnya, jika kita memiliki data tunggal dengan nilai 6 dan nilai rata-ratanya adalah 5, maka simpangan bakunya adalah 1. Hal ini menunjukkan bahwa data tersebut tidak terlalu bervariasi dari nilai rata-rata.
Contoh Soal Simpangan Baku Data Tunggal
Simpangan baku adalah ukuran sebaran data yang menunjukkan seberapa jauh nilai-nilai dalam suatu set data menyebar dari rata-rata. Semakin besar simpangan baku, semakin besar sebaran data, dan sebaliknya. Untuk memahami konsep ini, mari kita bahas contoh soal berikut.
Contoh Soal
Misalkan terdapat lima siswa dengan nilai ujian matematika sebagai berikut: 70, 80, 90, 85, dan 75. Hitunglah simpangan baku dari data nilai ujian matematika tersebut.
Langkah-langkah Penyelesaian
Berikut langkah-langkah untuk menghitung simpangan baku data tunggal:
- Hitung rata-rata (mean) dari data.
- Hitung selisih setiap nilai data dengan rata-rata.
- Kuadratkan setiap selisih.
- Jumlahkan semua kuadrat selisih.
- Bagi jumlah kuadrat selisih dengan jumlah data dikurangi 1.
- Akar kuadratkan hasil pembagian di langkah 5.
Penjelasan Konsep
Contoh soal ini menunjukkan bagaimana simpangan baku dapat diinterpretasikan dalam konteks nilai ujian matematika. Dalam contoh ini, simpangan baku menunjukkan seberapa jauh nilai ujian siswa menyebar dari rata-rata nilai ujian. Semakin besar simpangan baku, semakin besar sebaran nilai ujian, yang berarti nilai ujian siswa lebih bervariasi.
Interpretasi Hasil
Setelah menghitung simpangan baku, kita dapat menginterpretasikan hasilnya. Dalam contoh soal ini, jika simpangan baku nilai ujian matematika relatif kecil, hal ini menunjukkan bahwa nilai ujian siswa cenderung berkumpul di sekitar rata-rata. Sebaliknya, jika simpangan baku relatif besar, hal ini menunjukkan bahwa nilai ujian siswa lebih tersebar dan bervariasi.
Contoh Penerapan
Konsep simpangan baku memiliki banyak aplikasi dalam berbagai bidang, seperti:
- Statistik: Simpangan baku digunakan untuk mengukur sebaran data dalam berbagai penelitian statistik.
- Keuangan: Simpangan baku digunakan untuk mengukur risiko investasi.
- Kesehatan: Simpangan baku digunakan untuk mengukur variasi data kesehatan, seperti tekanan darah atau kadar gula darah.
Aplikasi Simpangan Baku Data Tunggal
Simpangan baku merupakan ukuran yang menunjukkan sebaran data dari rata-rata. Semakin besar simpangan baku, semakin besar sebaran data dari rata-rata. Sebaliknya, semakin kecil simpangan baku, semakin kecil sebaran data dari rata-rata.
Aplikasi Simpangan Baku dalam Berbagai Bidang
Simpangan baku data tunggal memiliki aplikasi yang luas di berbagai bidang, seperti statistik, ilmu sosial, dan ekonomi.
- Dalam statistik, simpangan baku digunakan untuk mengukur variabilitas data. Semakin besar simpangan baku, semakin besar variabilitas data. Hal ini membantu kita untuk memahami seberapa banyak data bervariasi dari rata-rata.
- Dalam ilmu sosial, simpangan baku digunakan untuk mengukur sebaran data demografis. Misalnya, kita dapat menggunakan simpangan baku untuk mengukur sebaran usia penduduk di suatu wilayah. Semakin besar simpangan baku, semakin besar sebaran usia penduduk. Ini membantu kita untuk memahami struktur usia penduduk di suatu wilayah.
- Dalam ekonomi, simpangan baku digunakan untuk mengukur volatilitas pasar saham. Semakin besar simpangan baku, semakin besar volatilitas pasar saham. Hal ini membantu investor untuk memahami risiko investasi di pasar saham.
Contoh Kasus Penggunaan Simpangan Baku
Berikut ini beberapa contoh kasus yang menunjukkan bagaimana simpangan baku digunakan untuk menganalisis data dalam berbagai bidang:
- Statistik: Misalkan kita ingin menganalisis tinggi badan siswa di suatu kelas. Kita memperoleh data tinggi badan siswa sebagai berikut: 160 cm, 165 cm, 170 cm, 175 cm, dan 180 cm. Simpangan baku dari data ini adalah 5 cm. Ini menunjukkan bahwa tinggi badan siswa di kelas tersebut bervariasi rata-rata 5 cm dari rata-rata tinggi badan mereka.
- Ilmu Sosial: Misalkan kita ingin menganalisis pendapatan penduduk di suatu kota. Kita memperoleh data pendapatan penduduk sebagai berikut: Rp 1.000.000, Rp 2.000.000, Rp 3.000.000, Rp 4.000.000, dan Rp 5.000.000. Simpangan baku dari data ini adalah Rp 1.581.138. Ini menunjukkan bahwa pendapatan penduduk di kota tersebut bervariasi rata-rata Rp 1.581.138 dari rata-rata pendapatan mereka.
- Ekonomi: Misalkan kita ingin menganalisis volatilitas harga saham PT. ABC selama satu tahun terakhir. Kita memperoleh data harga saham PT. ABC selama satu tahun terakhir sebagai berikut: Rp 10.000, Rp 11.000, Rp 12.000, Rp 13.000, dan Rp 14.000. Simpangan baku dari data ini adalah Rp 1.581.138. Ini menunjukkan bahwa harga saham PT. ABC selama satu tahun terakhir bervariasi rata-rata Rp 1.581.138 dari rata-rata harga saham mereka.
Pentingnya Memahami Konsep Simpangan Baku
Memahami konsep simpangan baku sangat penting dalam berbagai aplikasi praktis. Berikut beberapa alasannya:
- Membantu kita untuk memahami sebaran data: Simpangan baku menunjukkan seberapa banyak data bervariasi dari rata-rata. Hal ini membantu kita untuk memahami seberapa besar variabilitas data dan seberapa representatif rata-rata data.
- Membantu kita untuk membandingkan data: Simpangan baku dapat digunakan untuk membandingkan sebaran data dari dua kelompok data yang berbeda. Misalnya, kita dapat membandingkan sebaran tinggi badan siswa di dua kelas yang berbeda. Kelas dengan simpangan baku yang lebih besar memiliki sebaran tinggi badan yang lebih besar.
- Membantu kita untuk membuat keputusan yang lebih baik: Simpangan baku dapat digunakan untuk membuat keputusan yang lebih baik dalam berbagai bidang. Misalnya, dalam investasi, simpangan baku dapat digunakan untuk mengukur risiko investasi. Investor dapat menggunakan simpangan baku untuk memilih investasi dengan risiko yang lebih rendah.
Ringkasan Akhir
Memahami simpangan baku data tunggal akan membuka mata kita untuk melihat lebih dalam tentang sebaran data. Dengan memahami konsep ini, kita dapat menganalisis data dengan lebih baik dan mengambil keputusan yang lebih tepat. Mulailah dengan mempelajari contoh soal yang telah dibahas dan jangan ragu untuk mempraktikkannya dengan data-data yang kamu miliki.